回溯算法理論基礎

文章講解：代碼隨想錄#回溯算法理論基礎
視頻講解：帶你學透回溯算法（理論篇）| 回溯法精講！

什么是回溯法

回溯法也叫做回溯搜索法，是一種搜索的方式。
回溯是遞歸的副產品，只要有遞歸就會有回溯。
回溯法的效率并不高，它的本質就是窮舉法，有時候也會有剪枝的操作。

有些問題只有通過暴力窮舉才能解決，比如可以解決以下問題：

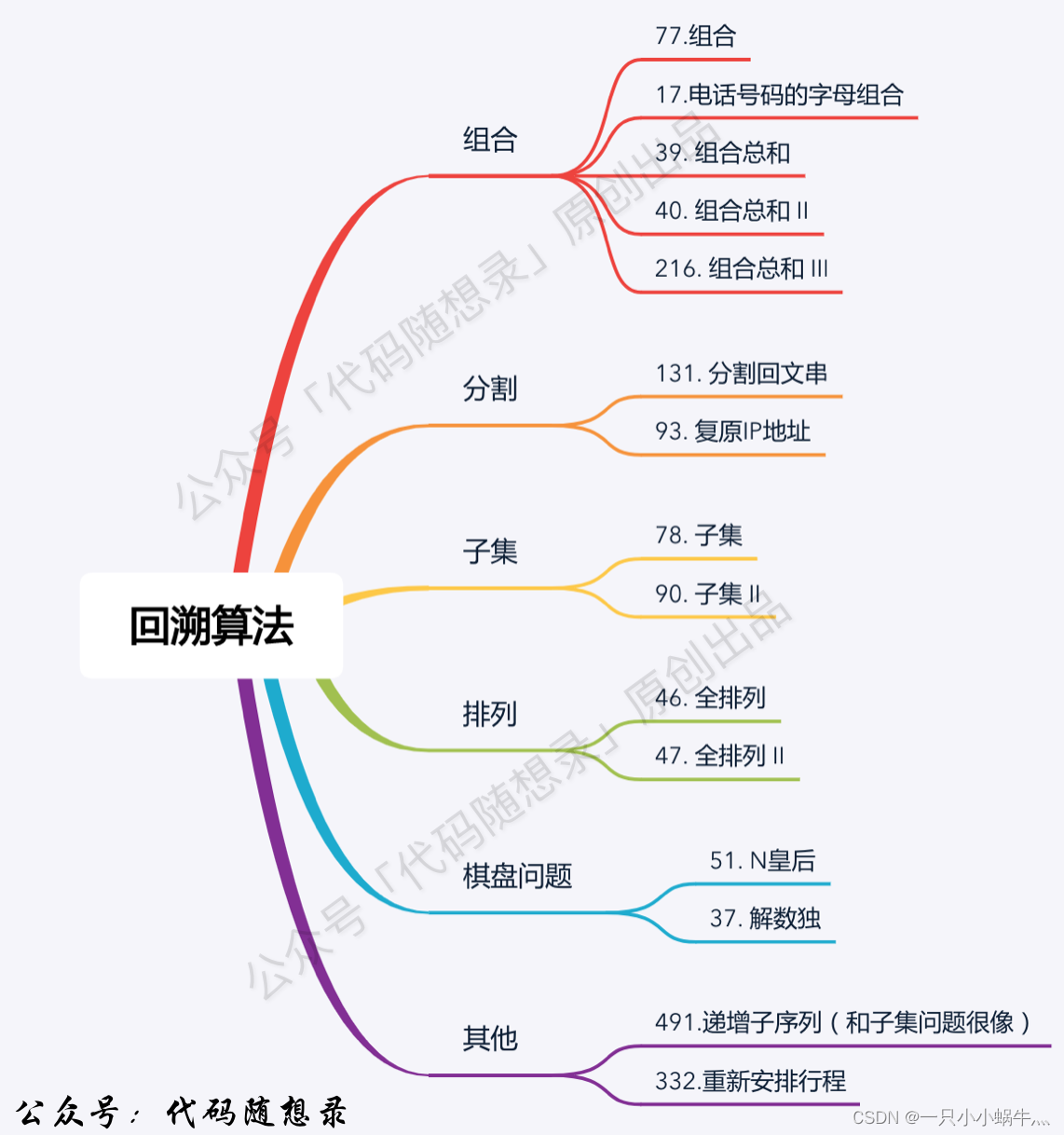
回溯法的理解

回溯法解決的問題都可以抽象成一個樹形結構。
回溯法解決的都是在集合中遞歸查找子集，集合的大小就構成了樹的寬度，遞歸的深度就構成了樹深度。
由于遞歸有終止條件，所以它是一棵高度有限的樹。

回溯法模板

遞歸有三部曲，同理回溯也有三部曲。

• 回溯函數體的返回值以及參數
  回溯算法中函數返回值一般為void。
  參數不能提前確定的，需要在根據處理邏輯來確定參數。
  所以回溯函數代碼如下

void backtracking(參數)

• 回溯函數終止條件
  一般情況下搜到葉子節點就找到了滿足條件的一種解決方法，需要將這個方法保存起來，同時要結束本層遞歸。

if (終止條件) {存放結果;return;
}

• 回溯搜索的遍歷過程
  回溯一般都是在集合中遞歸搜索 ，集合的大小構成了樹的寬度，遞歸的深度構成了樹的深度。

for(選擇：本層集合中元素(樹中節點孩子的數量就是集合的大小)){處理節點;backtracking(路徑，選擇列表); // 繼續遞歸回溯處理;
}

for循環就是遍歷集合區間，可以理解一個節點有多少個孩子，這個for循環就會執行多少次。
其實，for循環就是橫向遍歷，遞歸就是縱向遍歷。

回溯算法模板框架如下：

void backtracking(參數) {if (終止條件) {存放結果;return;}for (選擇：本層集合中元素（樹中節點孩子的數量就是集合的大小）) {處理節點;backtracking(路徑，選擇列表); // 遞歸回溯，撤銷處理結果}
}

---

LeetCode 77.組合

題目鏈接：77.組合
文章講解：代碼隨想錄#77.組合
視頻講解：帶你學透回溯算法-組合問題（對應力扣題目：77.組合）| 回溯法精講！

題目描述

給定兩個整數 n 和 k，返回范圍 [1, n] 中所有可能的 k 個數的組合。

你可以按 任何順序 返回答案。

示例1

輸入：n = 4, k = 2
輸出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例2

輸入：n = 1, k = 1
輸出：[[1]]

提示

• 1 <= n <= 20
• 1 <= k <= n

思路

這是一道經典的回溯題，求的是組合，并非排列。
對于組合，【1，2】和【2，1】是一回事，對于排列【1，2】和【2，1】不相同。
組合是不強調元素順序的，排列是強調元素順序。
所以，這道題中某個元素進行過組合后，就需要不能再重復計算了。

那如何使用回溯算法呢？
上面說過回溯的問題都可以抽象成樹形結構，盜圖說明一下。

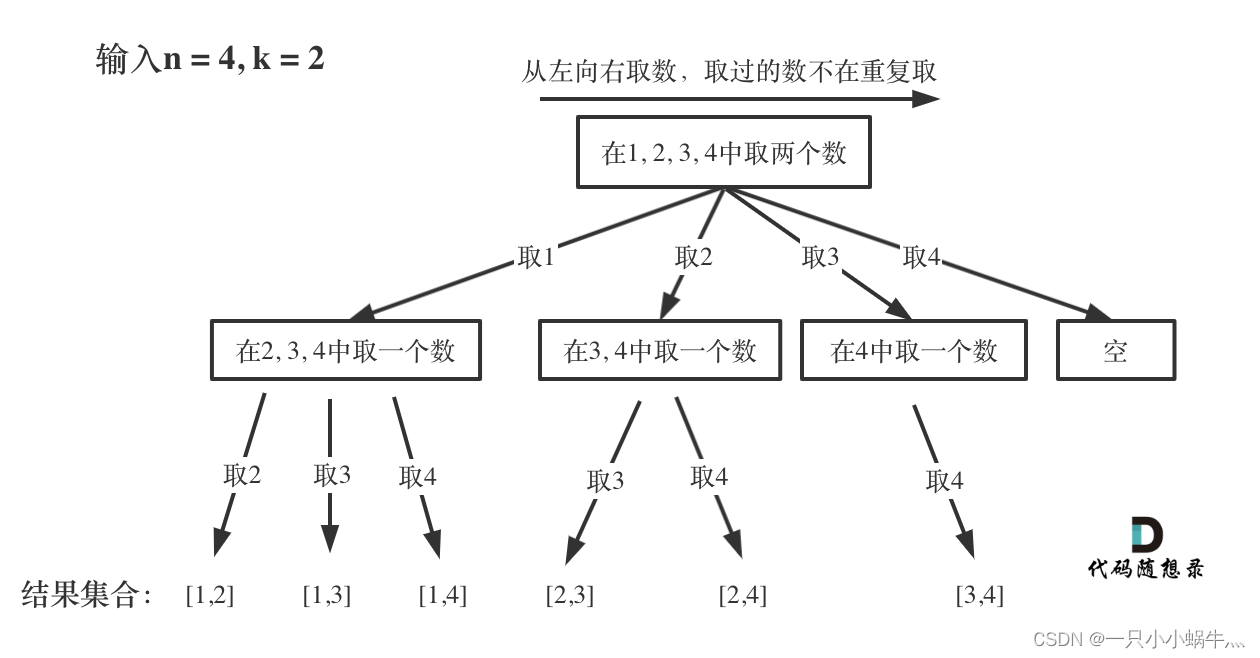
n相當于樹的寬度，k相當于樹的深度，每次搜索到葉子節點就表示找到了一個結果。

參考代碼

typedef struct {int index;int num[100];
}Result;Result result = {0};
int **res = NULL;
int cnt = 0;void backtracking(int n, int k, int idx)
{if (result.index == k) { // 終止條件，當result中已經放入了k個元素時res[cnt] = (int*)malloc(k * sizeof(int));for(int i = 0; i < k; i++) {res[cnt][i] = result.num[i];}cnt++;return;}for (int i = idx; i <= n; i++) { // 相當于樹的橫向遍歷result.num[result.index++] = i; // 處理節點backtracking(n, k, i + 1); // 遞歸遍歷下一層result.index--; // 回溯result.num[result.index] = 0;}
}int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {res = (int**)malloc(10000 * sizeof(int*));backtracking(n, k, 1);*returnSize = cnt;*returnColumnSizes = (int*)malloc(sizeof(int) * cnt); // 需要給returnColumnSizes分配內存for (int i = 0; i < cnt; i++) {(*returnColumnSizes)[i] = k;}return res;
}

總結

1. 代碼編譯報這個錯誤，網上查到說明變量沒有有效初始化，排查半天還是沒有發現問題出在哪兒。
   
2. 原因終于找到了，在力扣上不能在函數外面初始化全局變量，否則就會出現各種異常現象
   
   將如下修改，提交就AC了

修改后的代碼(微調整)

typedef struct {int index;int num[100];
}Result;Result result = {0};
int **res = NULL;
int cnt;  // ※※※ 切記：千萬不能在這塊初始化全局變量！！！void backtracking(int n, int k, int idx)
{if (result.index == k) { // 終止條件，當result中已經放入了k個元素時res[cnt] = (int*)malloc(k * sizeof(int));for(int i = 0; i < k; i++) {res[cnt][i] = result.num[i];}cnt++;return;}for (int i = idx; i <= n; i++) { // 相當于樹的橫向遍歷result.num[result.index++] = i; // 處理節點backtracking(n, k, i + 1); // 遞歸遍歷下一層result.index--; // 回溯result.num[result.index] = 0;}
}int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {res = (int**)malloc(200000 * sizeof(int*));cnt = 0; // 初始化全局變量backtracking(n, k, 1);*returnSize = cnt;*returnColumnSizes = (int*)malloc(sizeof(int) * cnt); // 需要給returnColumnSizes分配內存for (int i = 0; i < cnt; i++) {(*returnColumnSizes)[i] = k;}return res;
}

優化版本

對于部分回溯問題是可以通過減枝操作來優化效率的。
本題中可以進行減枝的地方就是循環遍歷的條件，想想我們需要k個數，如果在遍歷時n少于k時，那后面的循環遍歷就沒有必要了。
代碼中的循環條件為： (int i = idx; i <= n; i++)

可以進行如下的優化：
①已經選擇的元素個數為 result.index
②那還需要的元素個數為 k - result.index
③i為當前遍歷的元素位置，n - i 表示剩余的元素個數
那就這樣的關系： n - i + 1 >= k - result.index (剩余的元素個數要大于等于還需要的元素個數)
為什么要+1呢？因為是要包括當前的起始位置。

所以循環條件優化后為：for (int i = idx; i <= n - (k - result.index) + 1; i++)

優化后的參考代碼

typedef struct {int index;int num[100];
}Result;Result result = {0};
int **res = NULL;
int cnt;void backtracking(int n, int k, int idx)
{if (result.index == k) { // 終止條件，當result中已經放入了k個元素時res[cnt] = (int*)malloc(k * sizeof(int));for(int i = 0; i < k; i++) {res[cnt][i] = result.num[i];}cnt++;return;}for (int i = idx; i <= n - (k - result.index) + 1; i++)  { // 相當于樹的橫向遍歷result.num[result.index++] = i; // 處理節點backtracking(n, k, i + 1); // 遞歸遍歷下一層result.index--; // 回溯result.num[result.index] = 0;}
}int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {res = (int**)malloc(200000 * sizeof(int*));cnt = 0;backtracking(n, k, 1);*returnSize = cnt;*returnColumnSizes = (int*)malloc(sizeof(int) * cnt); // 需要給returnColumnSizes分配內存for (int i = 0; i < cnt; i++) {(*returnColumnSizes)[i] = k;}return res;
}