哈密頓路徑

Problem Statement:

問題陳述：

Given a graph G. you have to find out that that graph is Hamiltonian or not.

給定圖G。 您必須找出該圖是否為哈密頓量 。

Example:

例：

Input:

輸入：

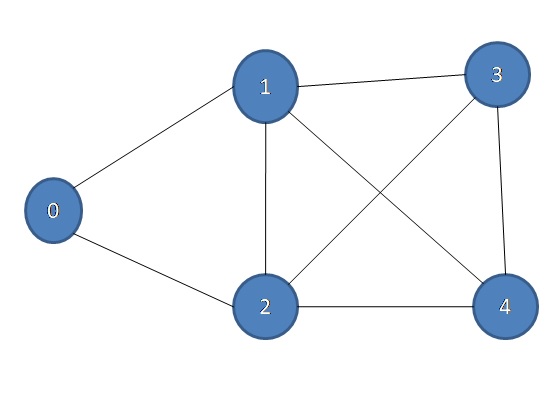
Output: 1

輸出1

Because here is a path 0 → 1 → 5 → 3 → 2 → 0 and 0 → 2 → 3 → 5 → 1 → 0

因為這里是路徑0→1→5→3→2→0和0→2→3→5→1→0

Algorithm:

算法：

To solve this problem we follow this approach:

為了解決這個問題，我們采用以下方法：

1. We take the source vertex and go for its adjacent not visited vertices.

   我們獲取源頂點，并尋找其相鄰的未訪問頂點。

2. Whenever we find a new vertex we make it source vertex and we repeat step 1.

   每當我們找到一個新頂點時，就將其設為源頂點，然后重復步驟1。

3. When a vertex count is equal to the vertex number then we check that from vertex is there any path to the source vertex. If there is exist a path to the source vertex then we will mark it and if not then make that vertex as unmarked and continue the process.

   當頂點數等于頂點數時，我們檢查從頂點開始是否存在到源頂點的任何路徑。 如果存在到源頂點的路徑，那么我們將對其進行標記，如果沒有，則將該頂點設為未標記并繼續該過程。

4. If there is no such path then we say NO.

   如果沒有這樣的路徑，那么我們說不。

檢查圖是否為哈密頓的C ++實現 (C++ Implementation to check a graph is Hamiltonian or not )

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void addedge(list<int>* g, int u, int v)
{
g[u].push_back(v);
g[v].push_back(u);
}
int hamiltonian(list<int>* g, int v, int s, int& count, bool* vis, int& h)
{
if (count > 1 && s == 0) {
h = 1;
return 1;
}
list<int>::iterator it;
for (it = g[s].begin(); it != g[s].end(); it++) {
if (!vis[*it]) {
vis[*it] = true;
count++;
if (count == v) {
vis[0] = false;
}
hamiltonian(g, v, *it, count, vis, h);
vis[0] = true;
vis[*it] = false;
count--;
}
}
return 0;
}
int main()
{
int num;
cin >> num;
for (int i = 0; i < num; i++) {
int v, e;
cin >> v >> e;
list<int> g[v];
int x, y;
for (int j = 0; j < e; j++) {
cin >> x >> y;
addedge(g, x, y);
}
bool vis[v];
memset(vis, false, sizeof(vis));
int count = 1;
vis[0] = true;
int h = 0;
hamiltonian(g, v, 0, count, vis, h);
cout << h << endl;
}
return 0;
}

Output

輸出量

1
5
8
0 1
0 2
1 2
1 3
1 4
3 4
3 2
2 4
1

翻譯自: https://www.includehelp.com/icp/check-a-graph-is-hamiltonian-or-not-hamiltonian-path.aspx

哈密頓路徑