Description:

描述：

This is a very popular interview problem to find all pair shortest paths in any graph. This problem has been featured in interview rounds of Samsung.

這是一個非常流行的面試問題，用于在任何圖中找到所有對最短路徑。 該問題已在三星的采訪回合中提到。

Problem statement:

問題陳述：

Given a weighted directed graph, the problem is to find the shortest distances between every pair of vertices. The Graph is represented by an adjacency matrix, and any cell arr[i][j] denotes the weight of the edge (path cost) from node i to node j (if it exists) else INF.

給定一個加權有向圖，問題在于找到每對頂點之間的最短距離。 該圖由鄰接矩陣表示，任何單元格arr [i] [j]表示從節點i到節點j (如果存在)或其他INF的邊的權重(路徑成本)。

Input: N=5

輸入： N = 5

Adjacency matrix:

鄰接矩陣：

Example:

例：

So the graph for the above input is,

因此，上述輸入的圖形為

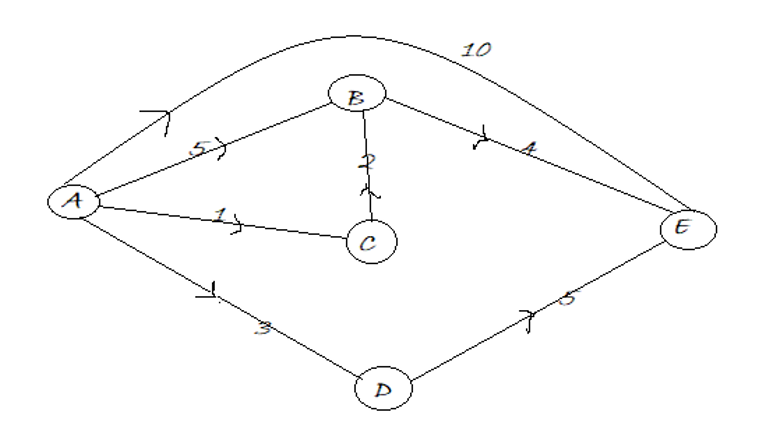
Figure 1: Directed Graph for which all pair shortest distance path needed to be found

圖1：有向圖，需要找到所有對的最短距離路徑

    A → B: 5
A → C: 1
A → D: 3
A → E: 10
B → A: INF
B → C: INF
B → D: INF
B → E: 4
C → A: INF
C → B: 2
C → D: INF
C → E: INF
D → A: INF
D → B: INF
D → C: INF
D → E: 5
E → A: INF
E → B: INF
E → C: INF
E → D: INF

Problem solution:

問題方案：

The Floyd Warshall algorithm computes the all pair shortest path in any weighted graph from the adjacency matrix. It also works for negative weight edges.

Floyd Warshall算法根據鄰接矩陣計算任何加權圖中的所有對最短路徑。 它也適用于負重量邊緣。

The algorithm is very simple to compute. Basically to compute the shortest path between i^th node to j^th node we check whether there is an intermediate node that reduces the distance, i.e., the path cost.

該算法非常容易計算。 基本上，為了計算第i ^個節點到^第 j ^個節點之間的最短路徑，我們檢查是否存在縮短距離的中間節點，即路徑成本。

Let,

讓，

    D(i,j) = Distance from ith node to ith node

We check for whether there is any intermediate node, say v such that,

我們檢查是否存在中間節點，例如v，

    D(i,u) + D(u,j) < D(i,j), for any intermidiate node u,u?[1,n]and u≠i,u≠j

Initially we consider the adjacency matrix to be the shortest distance table.

最初，我們認為鄰接矩陣是最短距離表。

Based on this concept, the Floyd-Warshall algorithm is designed.

基于此概念，設計了Floyd-Warshall算法。

So, initially the shortest distance table is,

因此，最短距離表最初是

After updating the shortest distance from A to other nodes,

更新了從A到其他節點的最短距離后，

So on.

等等。

C++ implementation:

C ++實現：

#include <bits/stdc++.h>
using namespace std;
void FloydWarshal(long long int** arr, int n)
{
for (int i = 0; i < n; i++) { //source node
for (int j = 0; j < n; j++) { //destination node
for (int k = 0; k < n; k++) { //intermediate node
// if shortest path via the intermediate node exists
if (arr[i][k] != INT_MAX && arr[k][j] != INT_MAX && arr[i][j] > arr[i][k] + arr[k][j])
arr[i][j] = arr[i][k] + arr[k][j]; //update shortest distance
}
}
}
cout << "Printing all pair shortest path distance\n";
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << char(i + 'A') << "->" << char(j + 'A') << ":";
if (arr[i][j] == INT_MAX)
cout << "INF"
<< "\n";
else
cout << arr[i][j] << "\n";
}
}
}
int main()
{
int n;
string item;
cout << "Number of node in the graph is:\n";
cin >> n;
long long int** arr = (long long int**)(malloc(sizeof(long long int*) * n));
cout << "Enter the weights\n";
//build the adjacency matrix
for (int j = 0; j < n; j++) {
arr[j] = (long long int*)(malloc(sizeof(long long int) * n));
for (int k = 0; k < n; k++) {
cout << "Enter weight of " << char(j + 'A') << " -> " << char(k + 'A') << endl;
cin >> item;
if (item == "INF")
arr[j][k] = INT_MAX;
else
arr[j][k] = stoi(item);
}
}
// function to compute all pair shortest distance
FloydWarshal(arr, n);
return 0;
}

Output

輸出量

Number of node in the graph is:
5
Enter the weights
Enter weight of A -> A
0
Enter weight of A -> B
5
Enter weight of A -> C
1
Enter weight of A -> D
3
Enter weight of A -> E
10
Enter weight of B -> A
INF
Enter weight of B -> B
0
Enter weight of B -> C
INF
Enter weight of B -> D
INF
Enter weight of B -> E
4
Enter weight of C -> A
INF
Enter weight of C -> B
2
Enter weight of C -> C
0
Enter weight of C -> D
INF
Enter weight of C -> E
INF
Enter weight of D -> A
INF
Enter weight of D -> B
INF
Enter weight of D -> C
INF
Enter weight of D -> D
0
Enter weight of D -> E
5
Enter weight of E -> A
INF
Enter weight of E -> B
INF
Enter weight of E -> C
INF
Enter weight of E -> D
INF
Enter weight of E -> E
0
Printing all pair shortest path distance
A->A:0
A->B:3
A->C:1
A->D:3
A->E:7
B->A:INF
B->B:0
B->C:INF
B->D:INF
B->E:4
C->A:INF
C->B:2
C->C:0
C->D:INF
C->E:6
D->A:INF
D->B:INF
D->C:INF
D->D:0
D->E:5
E->A:INF
E->B:INF
E->C:INF
E->D:INF
E->E:0

翻譯自: https://www.includehelp.com/icp/floyd-warshall-algorithm.aspx