自回歸模型（AR）：
①描述當前值和歷史值之間的關系，用變量自身的歷史時間數據對自身進行預測。
②自回歸模型必須滿足平穩性的要求。
③
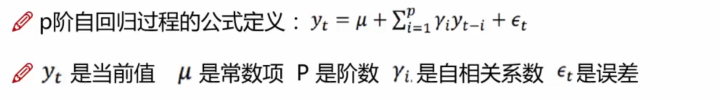
移動平均模型（MA）關注的是自回歸模型中的誤差項的累加。
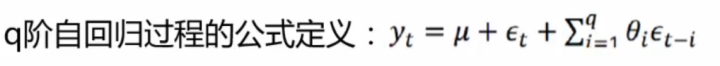
移動平均法能有效地消除預測中的隨機波動。
自回歸移動平均模型（ARMA）：
①自回歸與移動平均的結合
②
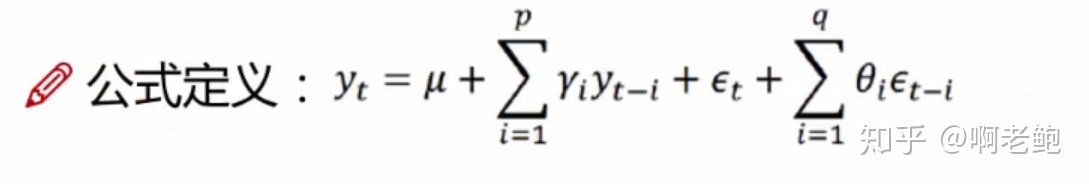
③易見，p和q都是我們需要指定的參數。
④原理：ARIMA模型將非平穩時間序列轉化為平穩時間序列，然后將因變量僅對它的滯后值（自回歸模型的階數p）以及隨機誤差項的現值和滯后值（MA的q）進行回歸所建立的模型。
為了確定參數p和q，下面先了解自相關函數ACF(自變量是p，因變量是相關系數)：
有序的隨機變量序列與其自身相比較，自相關函數反映了同一序列在不同時序的取值之間的相關性。
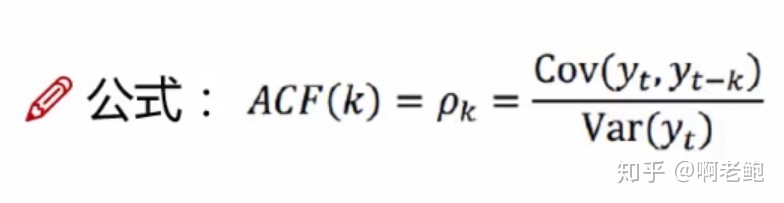
ACF（k）的取值范圍為[-1,1]。
ACF還包含了其他變量的影響，而偏自相關系數PACF是嚴格這兩個變量之間的相關性。
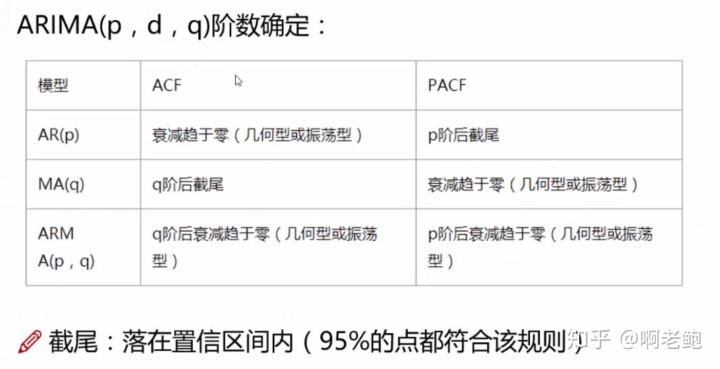
總結，ARIMA建模流程：將序列平穩（差分法確定d）；p和q階數確定；調用該模型
)
