1、引言

求解線性方程組在許多領域中都有重要應用，寫成矩陣的形式：

。

求解

可以寫成：

，這里需要求解矩陣

的逆。《線性代數》中給出的方法主要有兩類：

1、設置增廣矩陣，利用高斯消元法，通過初等行列變換可以求

但這種方法不利于使用計算機計算。

2、利用矩陣對角化求

這種方法關鍵在于求解矩陣

的特征值和特征向量，根據《線性代數》中給出求特征值和特征向量的方法，其復雜度大概是

，其中

是矩陣的行數，有個著名的算法SVD（singular value decomposition）。關于SVD的介紹已經很多了，今天我們想要更近一步，介紹另一種著名的矩陣對角化方法——

2、經典Jacobi方法

1846年數學家Jacobi提出的經典Jacobi方法用于求解實對稱矩陣的特征值。它的核心思想是采用一些列的Jacobi平面旋轉矩陣將對稱陣

變為對角陣

把

左右的Jacobi旋轉矩陣乘起來就是特征向量組成的特征矩陣，

為特征值組成的對角陣。Jacobi希望每通過一個Jacobi旋轉矩陣都能消去矩陣

中的

Jacobi旋轉矩陣定義如下：

一個Jacobi旋轉矩陣，對角線上只有第i行i列，j行j列為c，其余為1，未標出的元素均為0。

表示消去元素在矩陣

中的位置，其中

,

被稱為旋轉角，我們的目的就是找到一個合適的

，使得非對角元上的兩個元素變為0。由于

僅影響

行列的元素，故寫為二階主子式來表示旋轉變換過程：

其中

解得:

當一次變換結束后，

和

同時為0，而矩陣

的非對角元素的Frobenius norm的平方和將減少

[2]

其中

表示取A的對角線元素組成的對角矩陣。Frobenius norm的定義為：

3、復雜度分析

當

時，說明

被對角化了，其中

為精度要求。從貪心算法的角度來說，每次做旋轉都希望盡可能減少Frobenius norm，因此

的選擇矩陣

中最大的非對角元做旋轉變換。

但由于每次做旋轉變換后會影響矩陣

兩行兩列的數據，這會導致前面變成0的非對角元素在后續的變換中變為非0因此旋轉矩陣個數并不是

，同時在矩陣中尋找絕對值最大非對角元的復雜度也是

，而合并旋轉變換矩陣的部分復雜度為

，這在大規模矩陣中，遍歷元素將占絕大部分時間。

可能的改進方法

（1）循環Jacobi方法[3]

按照行順序或者列順序依次做Jacobi旋轉變換，持續多輪，直到滿足收斂條件。

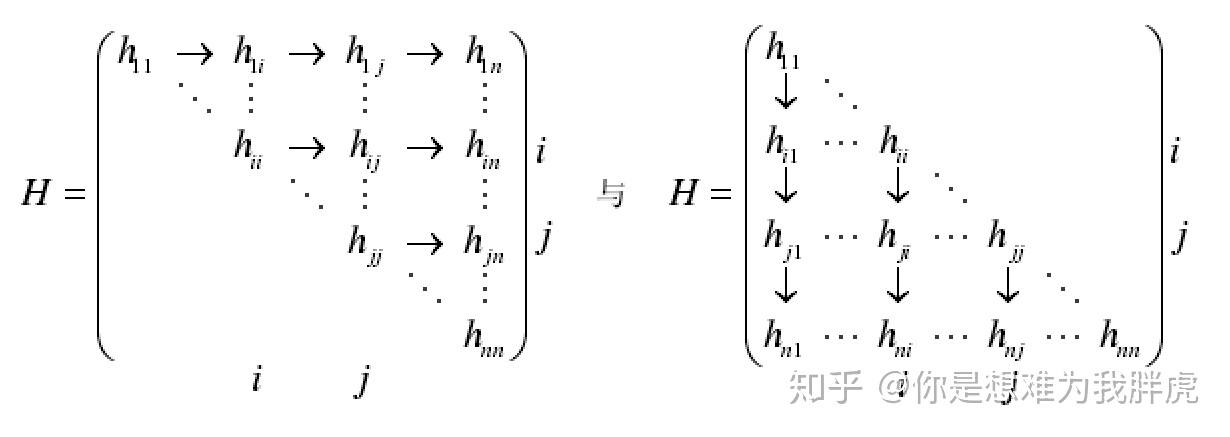
（2）過關Jacobi方法[4]

在順序遍歷的基礎上，在加入門限值，大于某個門限值，才做旋轉變換，其中門限值與

的Frobenius norm有關。

4、非對稱矩陣的Jacobi方法

對于非對稱矩陣

，可以將其構造為對稱矩陣

5、討論

高效使用Jacobi方法的關鍵在于，如何使用盡量少的旋轉角度完成對角化矩陣，貪心算法是否是最優方法還值得進一步探討。是否在矩陣中存在一個固定的最優的

的順序組合，還是說這與矩陣元素的具體取值有關。

參考文獻

[1] 郭強. 并行JACOBI方法求解矩陣奇異值的研究[D]. 蘇州大學.

[2] C.F. Van Loan G. H. Golub. Matrix COmputations[M]. John Hopkins University Press, Baltimore and London, second edition, 1993.

[3] E. R. Hansen. On Cyclic Jacobi Methods[J]. J.Soc,Indust.Appl.Math, 1963, 11(2): 448–459.

[4] B. N. Parlett. The Symmetric Eigenvalue Problem[M]. Prentice-Hall, 1980.