今天要給大家介紹的是這本書《Programming Quantum Computers —— Essential Algorithms and Code Samples》,主要講如何在量子計算機上編程,又示例的代碼可以跑 https://oreilly-qc.github.io./ ,這本書的理解方向是純粹計算機的,連矩陣都很少涉及,一個量子計算機就像是協處理器一樣,很像我們現在的GPU。
這本書一共分為三個部分,我也將分成三篇文章來寫。
單量子比特
這本書中對于量子的表達方式如下circle notation:

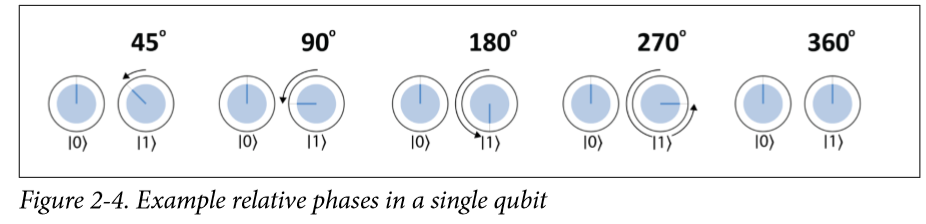
藍色圈的面積就是這個量子態測量后是這個狀態的概率,中間的藍色短線代表他們的相位,因為全局相位也觀察不出來,所以一般$|0\rangle$就是朝上的。對于一個量子比特來說,重要的也就這兩個,magnitude和relative phase(可能因為重要的是概率大小,所以他其實沒有提amplitude其實是一個復數)。

這兩個態實際上是等價的。
電路圖呢,一般長這樣
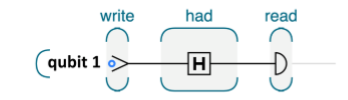
這個電路圖對應的代碼如下:(這個例子都可以在上面那個網站上跑起來)
qc.reset(1); // allocate one qubit
qc.write(0); // write the value zero
qc.had(); // place it into superposition of 0 and 1
var result = qc.read(); // read the result as a digital bit
第一步就是申請一個qubit,就像你要給變量分配空間一樣。
第二步寫0,其實寫0很容易,你可以直接測量,要么0,要么1,如果結果是1的話,再做一個not操作就好;當然,你要是嫌麻煩,對于一個qubit,長時間的靜置他,他也會變成0,畢竟還是基態比較穩定。
第三步就是進行一個H門的操作
第四步讀,其實就是測量了
常見的作用于單量子比特操作的表達方式:
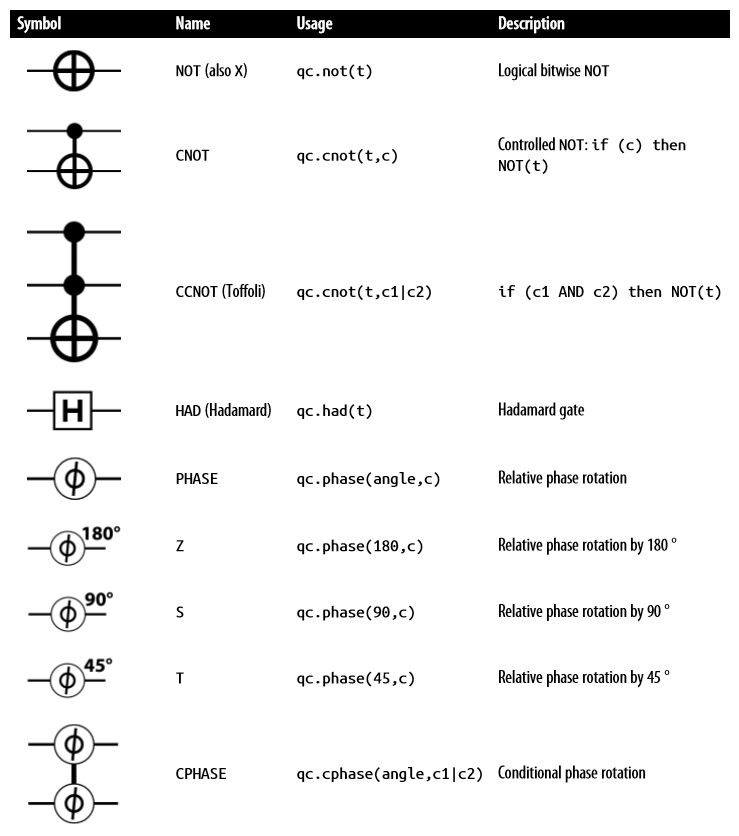

其中值得一提的是PHASE相位操作,phase操作只作用在 $|1\rangle$ 上,因為他的效果是改變相對相位,如果大家都改變就沒有什么用了。可能有同學聽說過繞X軸旋轉和繞Y軸旋轉,這些都是針對Bloch球的表達方式,與這里的circle notation的方式不要弄混了。
一個操作也可能是其他幾個操作的組合,比如:
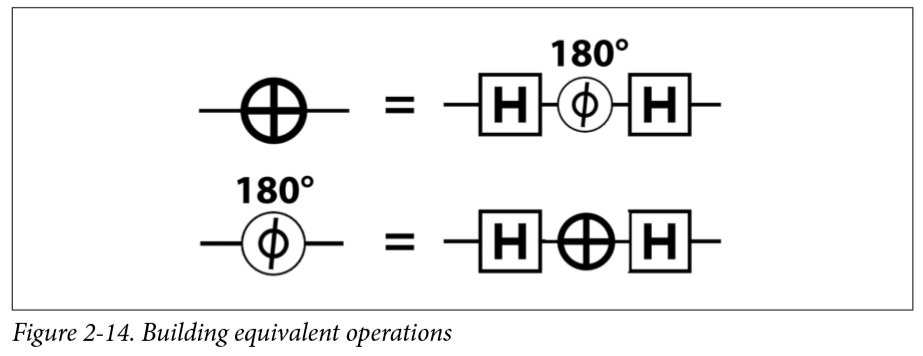
如果我們可以把not變成H+180°旋轉+H,那么我們也可以把中間的180°旋轉變成兩個90°的旋轉,中間再加上兩個H,因為$HH=I$,他們可以相互抵消,這樣我們還可以得到RNOT:

**COPY:**這是一個需要注意的操作,因為量子程序里沒有復制,這也保障了量子傳輸的信息不會被竊聽, 因為你要竊聽,你就需要去讀,一讀就是測量,而量子比特一測量就是坍縮。由于量子不能復制,所以,上述所有操作都是在原有的那個比特上操作的,所以操作就會被發現。
一個簡單例子:

對于這里例子來說, $A_1$ 和 $A_2$ 是對qubit Hadmard門操作后測量得到的隨機值,因為這個是真隨機,所以就不會被竊聽者提前知道或者預估,那么當我傳輸這個被我用紅色圈出來的比特的時候,spy并不知道這個比特是否執行了H門和not操作,那他就只能猜了,25%的概率,圖里面所示就是他猜有執行了,然后他再按照他的猜測如法炮制一個qubit繼續傳遞,當B收了這個bit后,B也隨機一個數據$B_2$,看是否執行H門,然后測量。這個時候消息也都收到了,測量也都測量好了,那么把 $A_2$的信息發過來也和竊聽沒有關系了,如果 $B_2$ $A_2$ 的結果一樣,那么測量結果應該一樣,如果不一樣,那么一定被竊聽了。
這樣的成功概率有多少呢? $B_2$ $A_2$ 一樣的概率0.5,在這種情況下spy被發現的概率0.25。看起來不是很高,但是如果我們有一百個比特先檢測一下這條線路,不被發現的概率將會降到百萬分之一。
qc.reset(3);//申請三個qubit
qc.discard();
var a = qint.new(1, 'alice'); //給其中一個變量命名為a,但是畫出來的電路圖中顯示alice
var fiber = qint.new(1, 'fiber');
var b = qint.new(1, 'bob');
function random_bit(q) {//對一個初始化為0的比特,進行H操作,然后測量,測量結果是隨機的
q.write(0);
q.had();
return q.read();
}
// Generate two random bits
qc.label('get two random bits');
var send_had = random_bit(a);//得到是否執行H門的隨機值
var send_value = random_bit(a);//得到是否not的隨機值
qc.label('');
// Prepare Alice's qubit
a.write(0);//a重新賦值為0,所以前面取隨機值的操作也可以在a上進行
qc.label('set value');
qc.nop();
if (send_value)
a.not();
qc.nop();
qc.label('');
qc.nop();
qc.label('apply had');
qc.nop();
if (send_had)
a.had();
qc.nop();
qc.label('');
// Send the qubit!
fiber.exchange(a);
// Activate the spy
var spy_is_present = true;
if (spy_is_present)
{
var spy_had = 1;
qc.nop();
qc.label('spy');
if (spy_had)
fiber.had();
stolen_data = fiber.read();
fiber.write(0);
if (stolen_data)
fiber.not();
if (spy_had)
fiber.had();
qc.label('');
qc.nop();
}
// Receive the qubit!
var recv_had = random_bit(b);
fiber.exchange(b);
qc.label('apply had');
qc.nop();
if (recv_had)
b.had();
qc.nop();
qc.label('');
qc.nop();
qc.label('read value');
qc.nop();
recv_val = b.read();
qc.nop();
qc.label('');
qc.nop();
// Now Alice emails Bob to tell
// him her had setting and value.
// If the had setting matches and the
// value does not, there's a spy!
if (send_had == recv_had)
if (send_value != recv_val)
qc.print('Caught a spy!\n');
多量子比特

多量子比特的表示方法和單量子比特沒有什么區別,下面的數字就是把他們從01的二進制換算成了我們熟悉的十進制。0x是十六進制的表示方法,最上面的是地位,正好可以not操作表示了出來,0就是000,1就是001,2就是010……以此類推
真要說和單量子比特的區別,那主要是兩方面,一個是糾纏;另一個就是受控操作。
糾纏
糾纏好說,兩個糾纏的量子比特就是其中一個的測量結果會影響另一個。
受控操作
受控操作就是說有兩類比特,一個是用來控制的,另一個是被控制的。
比如大家耳熟能詳的CNOT,當控制比特是1的時候,就翻轉被控制的比特,如果控制比特是0的時候,那就不做操作。還有CCNOT門,又叫做toffli門,有兩個控制比特,只有當他們都為1的時候才翻轉。
現在要介紹一個前面沒有提過的CPHASE受控相位門,和CNOT相似,同樣是當控制比特為1的時候才進行,但是正如前面我們提過,PHASE操作只操作在1上,也就是說,如果這個操作被執行其實只有一種情況,那就是$|11\rangle$ 。
在前面我們表示過一個旋轉180°的相位操作可以表示成一個 H+NOT+H figure 2-14
那么現在受控相位操作擁有了三種表示方法:

當控制比特為0的時候,CNOT就不會發生,兩個H又正好抵消了。
phase kickback
在這之所以說這么多的受控相位操作是因為這里面有個一很有趣的小技巧 QPU Trick: Phase Kickback 來看下面這個電路圖

這個電路圖很容易理解,一種理解方式就是把register 1當作控制比特,register 2 當作受控比特,兩個H門使得register 1變成了等可能的四種情況 $\frac{1}{2}|00\rangle+\frac{1}{2}|01\rangle+\frac{1}{2}|10\rangle+\frac{1}{2}|11\rangle$ 。
現在來看看結果:

因為register 2并不是疊加態,所以沒有相對相位,而絕對相位又測不出來,所以他可以說是沒有變的,改變了的,反而是register 1 , $|3\rangle$ 轉了135°是因為兩個都為1,45°和90°都轉了。作為一個受控操作,控制比特反而變了,而受控比特沒有改變。
swap
受控操作當然也能連在一起,得到一些有用的結果,比如三個CNOT操作,他就可以交換兩條線路。
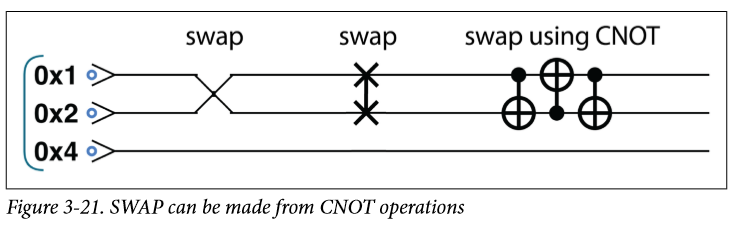
這個的證明是一件很容易的事情,你可以取一個任意態推一邊,專門把這個提出來說一遍是因為這個還能做一件有趣的事情,那就是驗證兩個比特是否相等。我們需要用到的是CSWAP,即當控制比特為1時才交換。
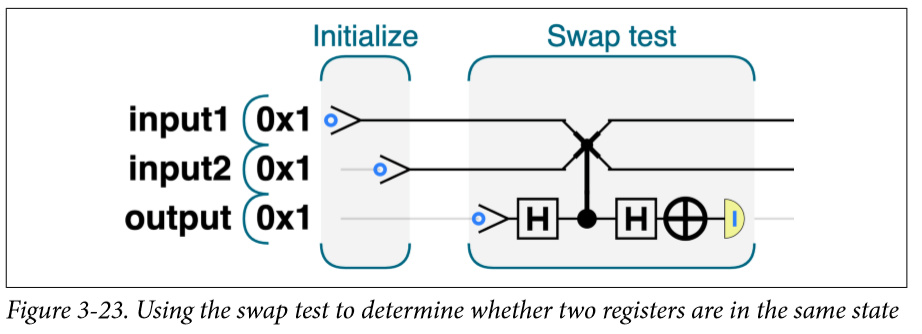
當我們的output比特經過H門后,他就變成了等概率的 $|0\rangle$ 和 $|1\rangle$ 經過一個CSWAP,為1情況下的input1和input2就會交換,也就是說他們原來x概率的ab就變成了x概率的ba了,這樣的問題出在哪?
如果概率還是原來的分布,那么在經過一個H門output等待率的 $|0\rangle$ 和 $|1\rangle$ 又會化簡成 $|0\rangle$ ,各種各樣的 $|1\rangle$ 的概率會相互抵消掉,那么在經歷一個NOT操作就一定會得到1。
那,如果這兩個數據不一樣,就一定得不到1嗎?不一定,只是他有概率不是1,而一旦有概率不是1,那只要多檢測幾次就一定能檢測出來,就像上面那個竊聽一樣,明明只有四分之一的概率,但僅需要一百次,測不出來的可能性就降到了百萬分之一。
受控操作當然不止這些,但是很多受控操作都可以分解成CNOT加上一些相位操作,我們可以自己構造自己需要的操作。
遠距離操控隨機
這里的遠距離操控不是指我能扣確定他是什么,如果我能確定,那就不是隨機了,而是說,我把兩個比特弄成糾纏,當我一個測出來是0的時候,另一個以x%的概率得到0,至于我測出來是不是0看天意,對面測出來是不是0,也看天意,其中唯一能確定的,就只有這個x了。
這個例子是書上例子3-6 https://oreilly-qc.github.io/?p=3-6 方法很簡單,就是我H門操作后,我旋轉45°的角度,這樣再來一個H門,因為相位變了,符號對不上,所以回不去了,就有了關聯。
更強大的一點的應用是——量子隱形傳態,量子隱形傳態 Quantum Teleportation 提過了,就不在累述。
原文出處:https://www.cnblogs.com/zmzzzz/p/12323743.html





)
)






和迭代器)



...)

