6.2.1二叉樹的性質
1.二叉樹
性質:
1.若二叉樹的層次從1開始,則在二叉樹的第i層最多有2^(i-1)個結點
2.深度為k的二叉樹最多有2^k -1個結點 (k>=1)
3.對任何一顆二叉樹,如果其葉結點個數為n0,度為2的非葉結點個數為n2,則有 n0=n2+1
4.具有n個結點的完全二叉樹的深度為 [log?n]+1 //log以2為底的n
5.
2.完全二叉樹:
特點:
1.只允許最后一層有空缺結點且空缺在右邊,即葉子結點只能在層次最大的兩層上出現;‘
2.對任一結點,如果其右子樹的深度為L,則其左子樹的深度必為 L 或 L+1
【總結】:
1.若每層僅有一個結點,則樹高h為1025;且其最小樹高為 log?1025 + 1=11,即h在11至1025之間。
2.深度為h的滿m叉樹共有mh-1個結點,第k層有mk-1個結點。
6.2.2二叉樹的存儲結構
1.順序存儲結構(數組表示)
n個結點的二叉樹,根節點編號為1,其余結點自上到下,自左到右編號,然后將完全二叉樹上編號為 i 的結點依次存儲在一維數組中下標為 i-1 的元素中。
代碼:
#define MAX_TREE_SIZE 100
typedef TElemTypeSqBiTree[MAX_TREE_SIZE];
SqBiTree bt;
:數組表示:沒有元素的結點也要空開相應位置
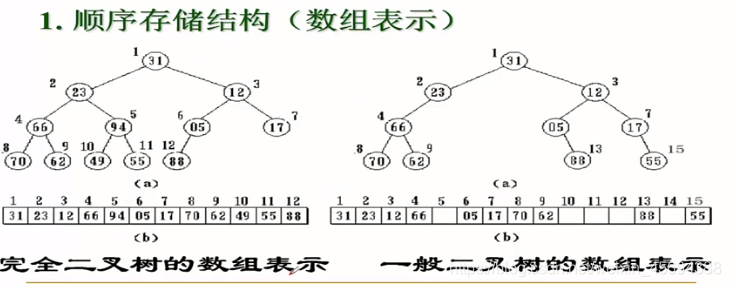
特點:非完全二叉樹就會浪費很多存儲空間,單支書就是一種極端情況,比如一個深度為k的有k個結點的單支書就需要2^k -1的一維數組
2.鏈式存儲結構
鏈表中一個結點相應地粗存儲二叉樹的一個結點
二叉鏈表:
每個結點包含兩個指針域和一個數據域,分別用來儲存指向二叉樹中結點的左右孩子的指針和結點信息
【圖】
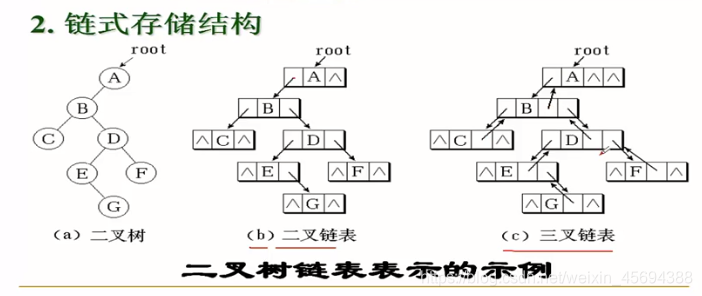
代碼
tyoedef sttuct BiTNode{
TElemType data;
Struct BiTNode*lchild,*rchild;
}BiTNode,*BiTree;三叉鏈表:
每個結點包含三個指針域和一個數據域用來指向該結點的雙親結點
【圖】
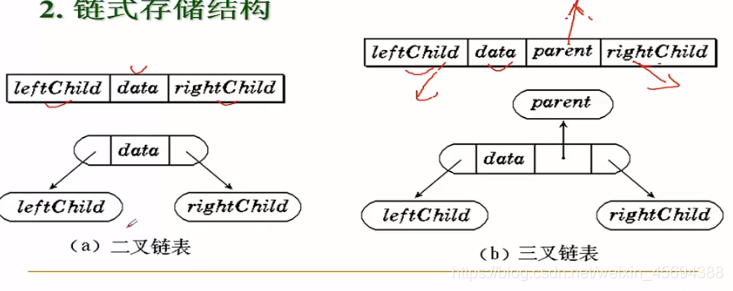

















)

和AOT(靜態編譯)編譯技術比較)