眾所周知，邏輯回歸常用于解決二分類任務，但是在工作/學習/項目中，我們也經常要解決多分類問題。本文總結了 3 種邏輯回歸解決多分類的方法，并分析了他們的優缺點。

---

一、One-Vs-Rest

假設我們要解決一個分類問題，該分類問題有三個類別，分別用▲，■ 和 × 表示，每個實例（Entity）有兩個屬性（Attribute），如果把屬性 1 作為 X 軸，屬性 2 作為 Y 軸，訓練集（Training Dataset）的分布可以表示為下圖：

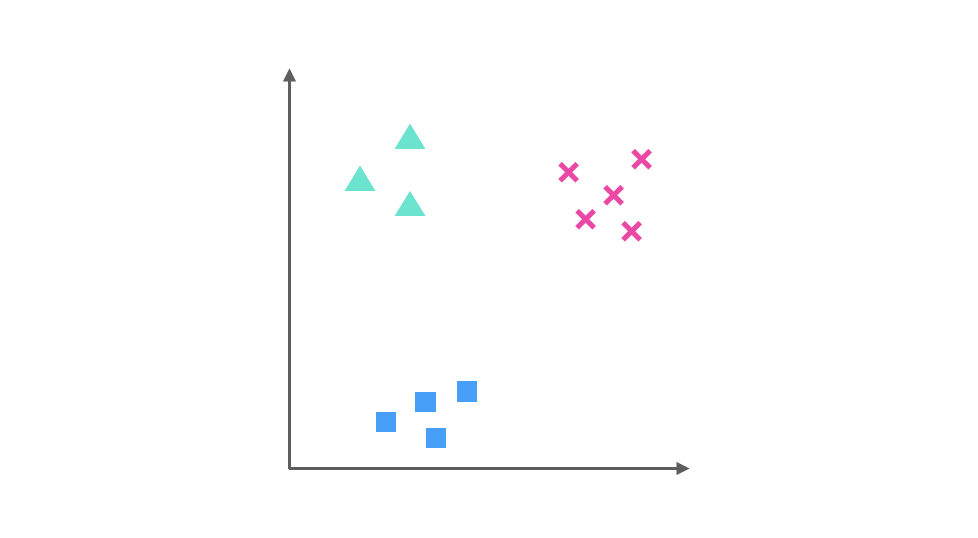
One-Vs-Rest 的思想是把一個多分類的問題變成多個二分類的問題。轉變的思路是選擇其中一個類別為正類（Positive），使其他所有類別為負類（Negative）。

比如第一步，我們將 ▲ 所代表的實例全部視為正類，其他實例全部視為負類，得到的分類器：

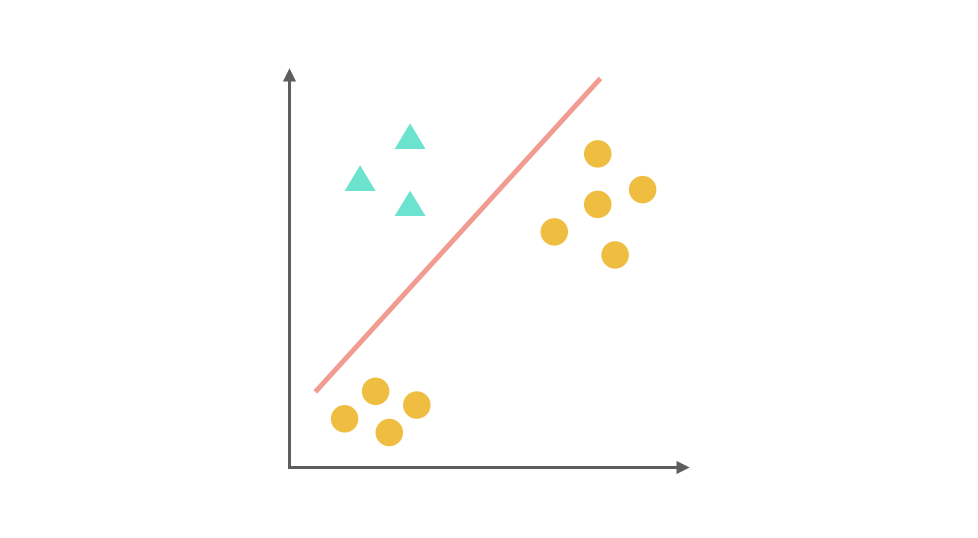
同理第二步，我們把 x 視為正類，其他視為負類，可以得到第二個分類器：

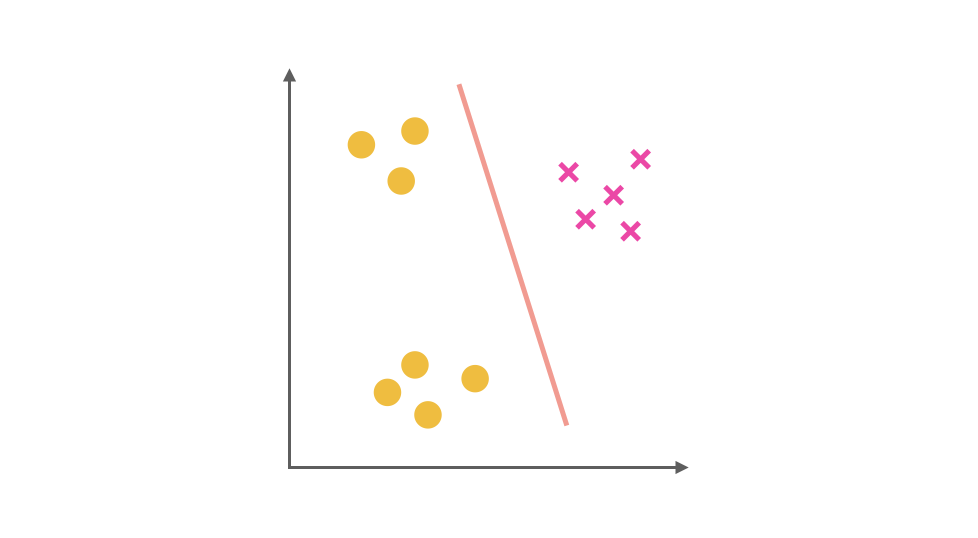
最后第三步，第三個分類器是把 ■ 視為正類，其余視為負類：

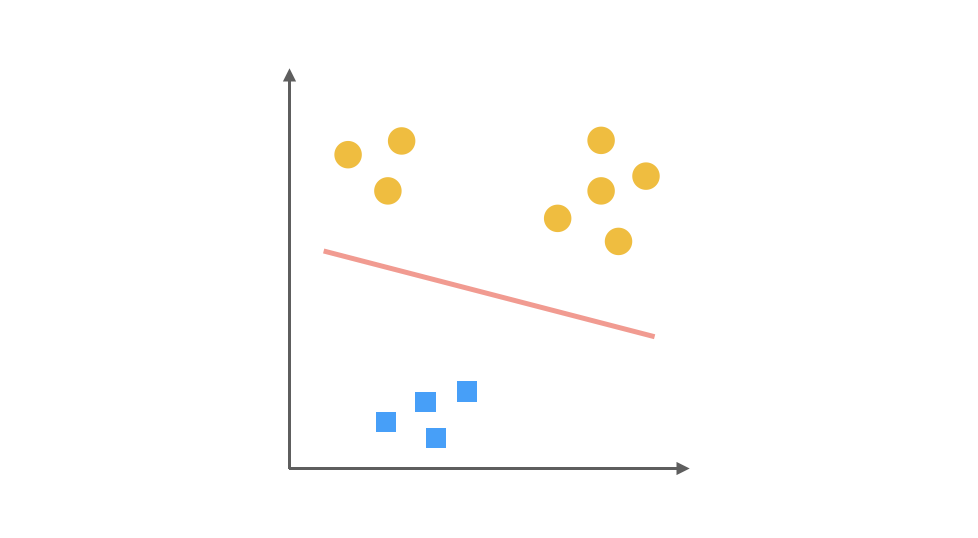
對于一個三分類問題，我們最終得到 3 個二元分類器。在預測階段，每個分類器可以根據測試樣本，得到當前正類的概率，即 P(y = i | x; θ)，i = 1, 2, 3。選擇計算概率結果最高的分類器，其正類就可以作為預測結果。

【優點】普適性比較廣，可以應用于能輸出值或者概率的分類器，同時效率相對較好，有多少個類別就訓練多少個分類器。

【缺點】很容易造成訓練集樣本數量的不平衡（Unbalance），尤其在類別較多的情況下，經常容易出現正類樣本的數量遠遠不及負類樣本的數量，這樣就會造成分類器的偏向性。

---

二、One-VS-One

相比于 One-Vs-Rest 由于樣本數量可能的偏向性帶來的不穩定性，One-Vs-One 是一種相對穩健的擴展方法。對于同樣的三分類問題，我們讓不同類別的數據兩兩組合訓練分類器，可以得到 3 個二元分類器。

它們分別是 ▲ 與 x 訓練得出的分類器：

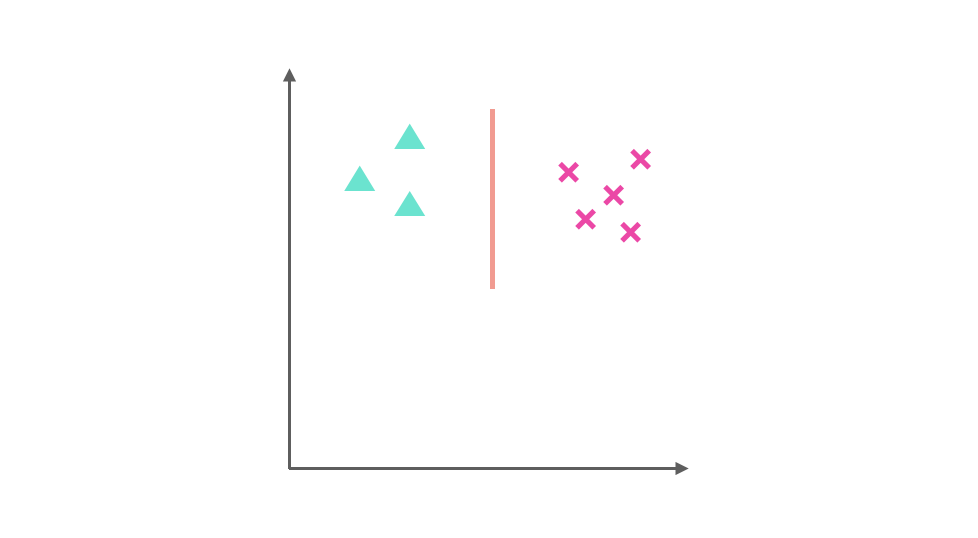
▲ 與 ■ 訓練的出的分類器：

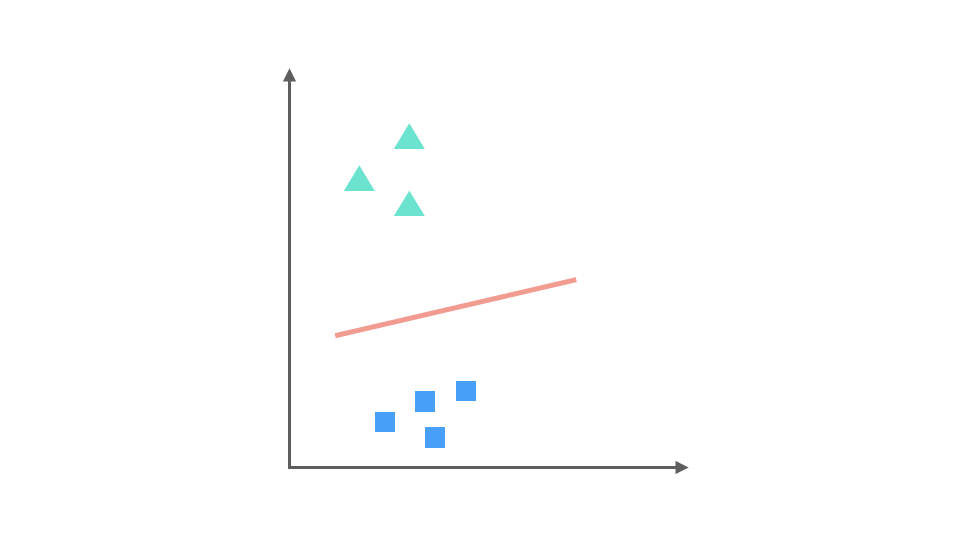
以及 ■ 與 x 訓練得出的分類器：

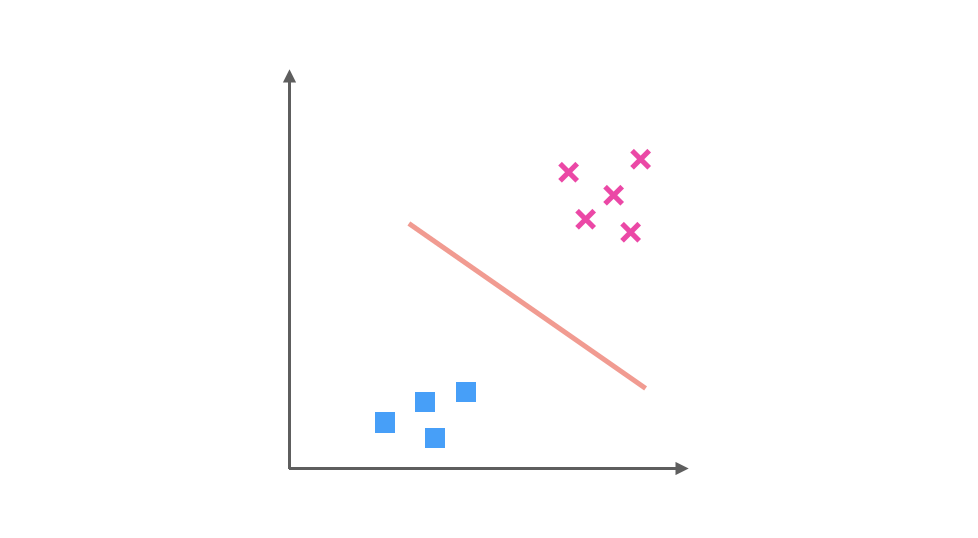
假如我們要預測的一個數據在圖中紅色圓圈的位置，那么第一個分類器會認為它是 x，第二個分類器會認為它偏向▲，第三個分類器會認為它是 x，經過三個分類器的投票之后，可以預測紅色圓圈所代表的數據的類別為 x。

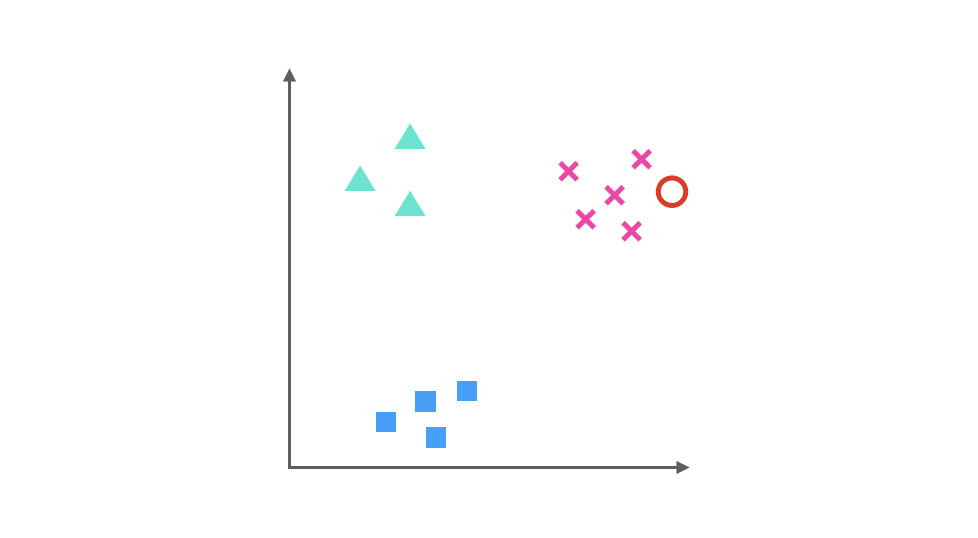
【優點】在一定程度上規避了數據集 unbalance 的情況，性能相對穩定，并且需要訓練的模型數雖然增多，但是每次訓練時訓練集的數量都降低很多，其訓練效率會提高。

【缺點】訓練出更多的 Classifier，會影響預測時間。如果有 k 個不同的類別，對于 One-Vs-All 來說，一共只需要訓練 k 個分類器，而 One-Vs-One 則需訓練 C(k, 2) 個分類器，只是因為在本例種，k = 3 時恰好兩個值相等，一旦 k 值增多，One-Vs-One 需要訓練的分類器數量會大大增多。

---

三、Softmax 函數

該模型將邏輯回歸推廣到分類問題，其中類標簽 y 可以采用兩個以上的可能值。這對于諸如MNIST數字分類之類的問題將是有用的，其中目標是區分10個不同的數字。

在softmax回歸中，我們對多類分類感興趣（而不是僅對二元分類），所以y可以取k個不同的取值。因此，在我們的訓練集

給定測試輸入 x ，我們希望模型估計每個類別的概率。因此，模型將輸出k維向量（其元素總和為1），給出 k 個類別的估計概率。具體地說，我們的假設

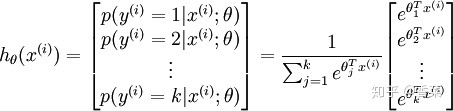
其中，

為方便起見，用向量法來表示模型的所有參數。當實現 softmax 回歸時，將θ表示為通過堆疊

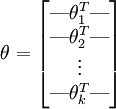
損失函數：

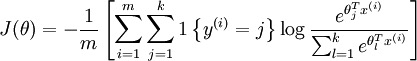
求導后，可得

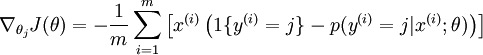
更新參數：

---

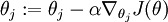
【注】 One-vs-Rest V.S. Softmax

假設正在處理音樂分類應用程序，并且正在嘗試識別 k 種類型的音樂。您應該使用softmax分類器，還是使用邏輯回歸構建k個單獨的二元分類器呢？這取決于這四個類是否相互排斥。如果類別之間是互斥的，softmax 會比較合適，如果類別之間不是互斥的，用 OvR 比較合適。

例如，如果四個類是經典，鄉村，搖滾和爵士樂，每個訓練樣例都標有這四個類別標簽中的一個，那么您應該構建一個 k = 4 的 softmax 分類器，因為這些標簽都是互斥的。但是，如果類別是舞蹈，配樂，流行音樂，那這些并不相互排斥，因為可以有一段來自音軌的流行音樂，另外還有人聲。在這種情況下，構建 4 個二元邏輯回歸分類器更合適。這樣，對于每個新的音樂作品，算法可以單獨決定它是否屬于四個類別中的每一個。

總結，如果類別之間是互斥的，那么用 softmax 會比較合適，如果類別之間不是互斥的，用 OvR 比較合適。

參考：

[1]

力扣（LeetCode）：3 種方法實現邏輯回歸多分類?zhuanlan.zhihu.com

[2]

飛魚Talk：邏輯回歸 - 4 邏輯回歸與多分類?zhuanlan.zhihu.com