公眾號關注?“ML_NLP”設為 “星標”，重磅干貨，第一時間送達！

機器學習算法與自然語言處理出品

@公眾號原創專欄作者?思婕的便攜席夢思

單位 |?哈工大SCIR實驗室

KL散度 = 交叉熵 - 熵

1. 1. 熵(Entropy)

抽象解釋：熵用于計算一個隨機變量的信息量。對于一個隨機變量X，X的熵就是它的信息量，也就是它的不確定性。
形象例子：有兩個隨機變量X和Y，或者說兩個事件，X表示“投一枚硬幣，落地時，哪一面朝上”；Y表示“太陽從哪個方向升起”。對于隨機變量X，“正面朝上”和“反面朝上”的概率各為0.5；對于隨機變量Y，“太陽從東邊升起”的概率為1，從另外三個方向升起的概率為0。由此可以看出，事件X的不確定性大于事件Y，因此事件X的熵也就大于事件Y。
那么具體該如何計算熵呢？
熵的數學定義為：

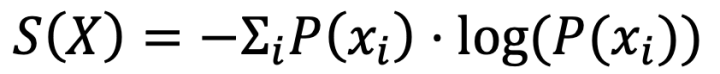
舉個例子，依舊是投硬幣的那個事件：
我們令

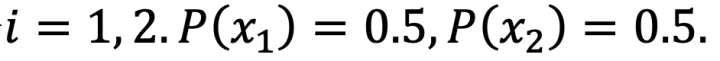
那么它的熵為：

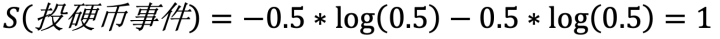
從編碼的角度理解熵
對于任意一個離散型隨機變量，我們都可以對其進行編碼。例如我們可以把字符看出一個離散型隨機變量。
根據shannon的信息論，給定一個字符集的概率分布，我們可以設計一種編碼，使得表示該字符集組成的字符串平均需要的比特數最少。假設這個字符集是X，對x∈X，其出現概率為P(x)，那么其最優編碼(哈夫曼編碼)平均需要的比特數等于這個字符集的熵。

1. 1. KL散度(Kullback-Leibler divergence)

抽象解釋：KL散度用于計算兩個隨機變量的差異程度。相對于隨機變量X，隨機變量Y有多大的不同？這個不同的程度就是KL散度。KL散度又稱為信息增益，相對熵。需要注意的是KL散度是不對稱的，就是說：X關于Y的KL散度 不等于 Y關于X的KL散度。
形象例子：
X表示“不透明的袋子里有2紅2白五個球，隨機抓一個球，球的顏色”事件，
Y表示“不透明的袋子里有3紅2白五個球，隨機抓一個球，球的顏色”事件，
Z表示“不透明的袋子里有1紅1白兩個球，隨機抓一個球，球的顏色”事件。
由于在事件X和Z中，都是P(紅)=0.5 P(白)=0.5；而在事件Y中P(紅)=0.6 P(白)=0.4，所以我們認為：相對于事件X，事件Y的差異程度小于事件Z。
那么該如何具體計算KL散度呢？
KL散度的數學定義為：
對于離散型隨機變量，我們定義A和B的KL散度為：

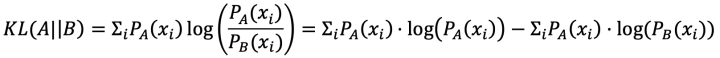
對于離散型隨機變量，我們定義A和B的KL散度為：

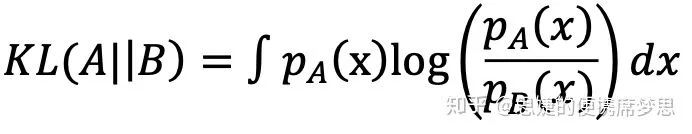
從編碼的角度理解KL散度
在同樣的字符集上，假設存在另一個概率分布Q(X)。如果用概率分布P(X)的最優編碼(即字符x的編碼長度等于log[1/P(x)])，來為符合分布Q(X)的字符編碼，那么表示這些字符就會比理想情況多用一些比特數。KL-divergence就是用來衡量這種情況下平均每個字符多用的比特數，因此可以用來衡量兩個分布的距離。

1. 1. 交叉熵(Cross-Entropy)

抽象解釋：我所理解的交叉熵的含義，與KL散度是類似的，都是用于度量兩個分布或者說兩個隨機變量、兩個事件不同的程度。
具體例子：與KL散度類似
交叉熵的數學定義：

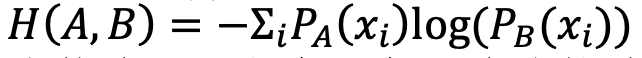
比較熵、KL散度和交叉熵的數學定義會發現：
KL散度 = 交叉熵 - 熵
從編碼的角度理解交叉熵熵的意義是：對一個隨機變量A編碼所需要的最小字節數，也就是使用哈夫曼編碼根據A的概率分布對A進行編碼所需要的字節數；KL散度的意義是：使用隨機變量B的最優編碼方式對隨機變量A編碼所需要的額外字節數，具體來說就是使用哈夫曼編碼卻根據B的概率分布對A進行編碼，所需要的編碼數比A編碼所需要的最小字節數多的數量；交叉熵的意義是：使用隨機變量B的最優編碼方式對隨機變量A編碼所需要的字節數，具體來說就是使用哈夫曼編碼卻根據B的概率分布對A進行編碼，所需要的編碼數。

推薦閱讀：

【長文詳解】從Transformer到BERT模型

賽爾譯文 | 從頭開始了解Transformer

百聞不如一碼！手把手教你用Python搭一個Transformer