latex 算法_GitHub項目awesome-latex-drawing新增內容（四）：繪制貝葉斯網絡

393ee631c749a84cec9518f43b5c1edd.png
近期，我們整理和開源了一個基于LaTeX的科技繪圖項目，并將其取名為awesome-latex-drawing（GitHub網址為：https://github.com/xinychen/awesome-latex-drawing），案例包括貝葉斯網絡、圖模型、矩陣/張量示意圖以及技術框架，所有案例均取自于我們近期的研究工作。截至目前，awesome-latex-drawing項目已在GitHub社區獲得超過500次標星 (star)。

需要說明的是，本文轉載自awesome-latex-drawing項目，如需閱讀本文代碼以及相關的說明文檔，歡迎訪問tutorial/Bayesian_nets.md。

一、基本介紹

貝葉斯網絡是一種應用極為廣泛的概率圖模型，由節點和有向邊構成，能夠通過有向邊來描述變量之間的條件依賴關系。給定一個已經構造好的貝葉斯網絡，通常可以采用一些貝葉斯推斷算法對其中的變量進行推斷或者學習，這些貝葉斯推斷算法中既包括最為人所熟知的馬爾可夫鏈蒙特卡洛算法，也包括形式上略顯抽象的變分推斷算法。

直觀清晰的貝葉斯網絡結構圖可以幫助讀者和研究者更好地理解貝葉斯網絡，而LaTeX在繪制貝葉斯網絡結構方面具有天然的優勢，一是由于我們在使用LaTeX繪圖的過程中，LaTeX能夠最大程度上支持復雜的公式符號；二則得益于LaTeX的一系列兼容性極好的圖模型繪制包，其中，最具代表性且使用最為廣泛的工具庫(對應于LaTeX則稱為library)莫過于bayesnet。結合LaTeX中的繪圖工具包tikz，我們可以使用LaTeX畫出近乎完美的貝葉斯網絡。

bayesnet庫是基于LaTeX繪圖工具包tikz構建起來的貝葉斯網絡繪圖工具庫，主要用于繪制貝葉斯網絡、圖模型以及有向圖結構，其GitHub開發主頁為https://github.com/jluttine/tikz-bayesnet。

本文將對幾個具有代表性的貝葉斯網絡案例進行拆分講解，通過介紹各行代碼及其所對應的繪圖圖形，逐步講解如何用LaTeX繪制出復雜的貝葉斯網絡，在開始繪圖之前，我們不妨回顧一下貝葉斯網絡所遵循的幾項繪圖原則：

  • 觀測變量或者觀測值要使用灰色節點表示；
  • 底層超參數無需用節點表示；
  • 除觀測變量和底層超參數外的其他變量要使用白色節點表示；
  • 有向邊箭頭的指向表示貝葉斯角度的概率依賴關系。

為了方便廣大讀者體驗LaTeX繪圖，我們在在線LaTeX編輯系統overleaf.com中創建名稱為latex-drawing-tutorial的項目，接下來就在項目中開啟貝葉斯網絡的LaTeX繪圖之旅。

二、繪制貝葉斯網絡的基本語句

使用LaTeX繪制貝葉斯網絡時，我們需要用到一些最為基本的LaTeX命令：

documentclass[tikz, border = 0.1cm]{standalone}
usepackage{tikz}
usetikzlibrary{bayesnet}
usepackage{amsmath, amsthm, amssymb, amsfonts}
tikzset{>=latex}begin{document}
begin{tikzpicture}end{tikzpicture}
end{document}

在這幾行基本命令中，它們各自都發揮著一定的作用，我們不妨來逐行看一下這些命令的“功效”：

  • 準備階段：
    • documentclass[tikz, border = 0.1cm]{standalone}的作用在于指定所創建文件的類型，確定tikz繪圖風格的同時可設置繪圖邊框的頁邊距，這里選取的頁邊距是0.1厘米。當然，這里的頁邊距是可以根據我們自身的審美標準進行設置的。
    • usepackage{tikz}的作用在于啟用LaTeX中的繪圖工具包tikz。
    • usetikzlibrary{bayesnet}的作用在于調用繪制貝葉斯網絡所需的bayesnet庫。
    • usepackage{amsmath, amsthm, amssymb, amsfonts}的作用在于啟用LaTeX中支持公式編譯的工具包。
  • 繪圖階段：
    • begin{document} end{document}是LaTeX編輯各類文檔時首先要申明的語句，在begin和end之間寫語句才能有效地映射到所創建的文檔中。
    • begin{tikzpicture} end{tikzpicture}是用于生成tikz繪圖的基本語句，在tikzpicture中，我們可以通過指定各個節點(node)的橫縱坐標來進行繪圖。

三、繪制貝葉斯增強張量分解的貝葉斯網絡

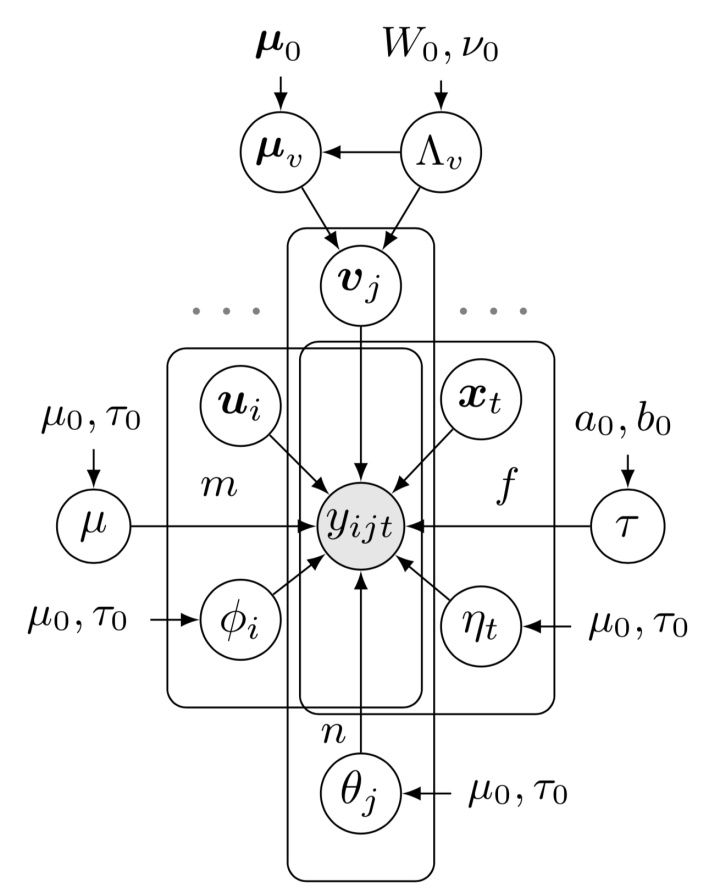
繪圖任務：如何使用LaTeX繪制出如下貝葉斯增強張量分解的貝葉斯網絡？

d4ead86969a59e3e77f2af84809dc4a4.png
圖: 貝葉斯增強張量分解的貝葉斯模型示意圖

1) 繪制觀測變量節點

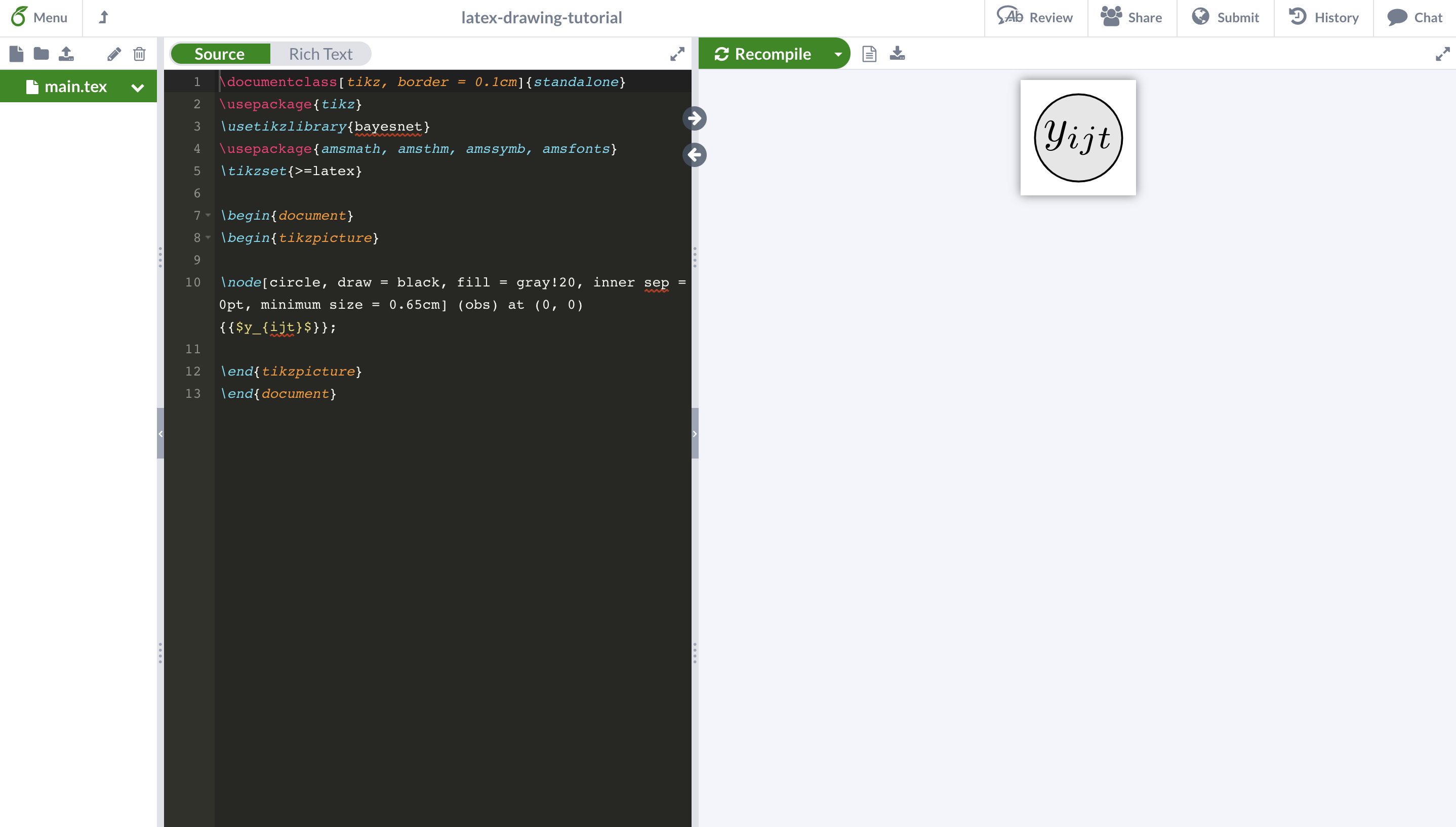
以上述的幾行LaTeX繪圖的基本命令為基礎，我們不妨在begin{tikzpicture} end{tikzpicture}之間編寫關于繪制觀測變量節點的代碼：首先，我們將觀測變量節點命名為obs，在node命令中，指定該節點的位置為坐標原點(0,0)，指定節點類型為circle，另外令節點邊框為黑色（即draw = black）、節點大小為0.65厘米（即minimum size = 0.65cm）。

documentclass[tikz, border = 0.1cm]{standalone}
usepackage{tikz}
usetikzlibrary{bayesnet}
usepackage{amsmath, amsthm, amssymb, amsfonts}
tikzset{>=latex}begin{document}
begin{tikzpicture}node[circle, draw = black, fill = gray!20, inner sep = 0pt, minimum size = 0.65cm] (obs) at (0, 0) {{$y_{ijt}$}};end{tikzpicture}
end{document}

將這幾行簡單的代碼復制粘貼到所創建的overleaf項目中，即可得到的觀測變量節點示意圖。另外，從下圖可以看出，左側為代碼區域，右側為畫圖文檔區域。

de1fd6c8c800def851af5449adbc07b2.png
圖: 繪制貝葉斯模型的觀測變量節點

2) 繪制模型參數節點

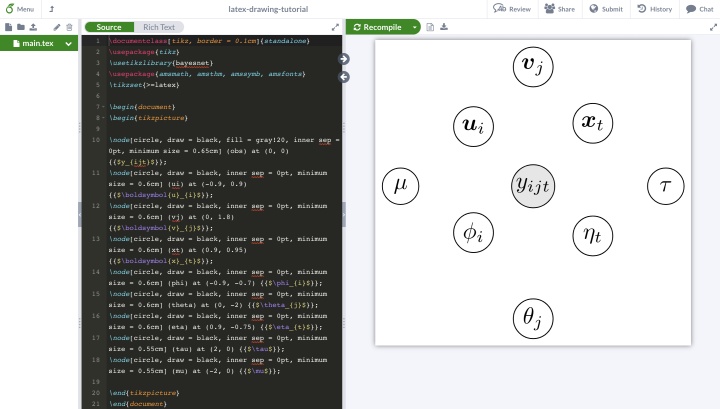
與繪制觀測變量節點類似，我們可以通過node設計模型參數節點。

documentclass[tikz, border = 0.1cm]{standalone}
usepackage{tikz}
usetikzlibrary{bayesnet}
usepackage{amsmath, amsthm, amssymb, amsfonts}
tikzset{>=latex}begin{document}
begin{tikzpicture}node[circle, draw = black, fill = gray!20, inner sep = 0pt, minimum size = 0.65cm] (obs) at (0, 0) {{$y_{ijt}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (ui) at (-0.9, 0.9) {{$boldsymbol{u}_{i}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (vj) at (0, 1.8) {{$boldsymbol{v}_{j}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (xt) at (0.9, 0.95) {{$boldsymbol{x}_{t}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (phi) at (-0.9, -0.7) {{$phi_{i}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (theta) at (0, -2) {{$theta_{j}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (eta) at (0.9, -0.75) {{$eta_{t}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.55cm] (tau) at (2, 0) {{$tau$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.55cm] (mu) at (-2, 0) {{$mu$}};end{tikzpicture}
end{document}

同樣，將這里的代碼復制并粘貼到所創建的overleaf項目中，即可得到觀測變量節點和模型參數節點示意圖。

0927a9e6c8a7f70fa88f8bfd2f68dbb7.png
圖: 新增貝葉斯模型的模型參數節點

3) 繪制模型參數節點和觀測變量節點之間的有向邊

緊接著上面繪制觀測變量節點和模型參數節點的代碼，根據已經定義好的節點，可以使用path來構造有向邊，其中模型參數節點和觀測變量節點之間要用edge關聯，箭頭方向為->。

documentclass[tikz, border = 0.1cm]{standalone}
usepackage{tikz}
usetikzlibrary{bayesnet}
usepackage{amsmath, amsthm, amssymb, amsfonts}
tikzset{>=latex}begin{document}
begin{tikzpicture}node[circle, draw = black, fill = gray!20, inner sep = 0pt, minimum size = 0.65cm] (obs) at (0, 0) {{$y_{ijt}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (ui) at (-0.9, 0.9) {{$boldsymbol{u}_{i}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (vj) at (0, 1.8) {{$boldsymbol{v}_{j}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (xt) at (0.9, 0.95) {{$boldsymbol{x}_{t}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (phi) at (-0.9, -0.7) {{$phi_{i}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (theta) at (0, -2) {{$theta_{j}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (eta) at (0.9, -0.75) {{$eta_{t}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.55cm] (tau) at (2, 0) {{$tau$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.55cm] (mu) at (-2, 0) {{$mu$}};path [draw, ->] (ui) edge (obs);
path [draw, ->] (vj) edge (obs);
path [draw, ->] (xt) edge (obs);
path [draw, ->] (tau) edge (obs);
path [draw, ->] (mu) edge (obs);
path [draw, ->] (phi) edge (obs);
path [draw, ->] (theta) edge (obs);
path [draw, ->] (eta) edge (obs);end{tikzpicture}
end{document}

將這里的代碼復制并粘貼到所創建的overleaf項目中，即可得到觀測變量節點、模型參數節點以及有向邊示意圖。

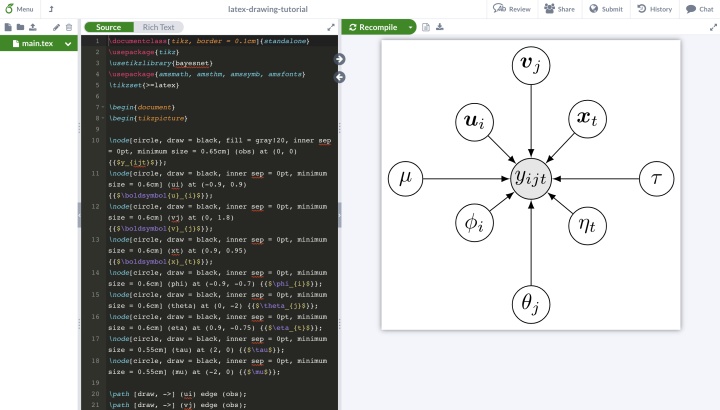
237300ccf3b375e80e21a8e012d2028c.png
圖: 新增貝葉斯模型觀測變量節點和模型參數節點之間的有向邊

4) 繪制部分觀測變量的元素集合

對于部分觀測變量，它可能只包括矩陣或張量元素的部分索引，因此需要指定出來。一般而言，我們可以用plate在貝葉斯網絡中進行標注，標注的方法是在plate命令中羅列需要覆蓋的變量。以第一個plate為例，我們可以將{(obs) (ui) (m) (phi)}作為所需要覆蓋的集合。

documentclass[tikz, border = 0.1cm]{standalone}
usepackage{tikz}
usetikzlibrary{bayesnet}
usepackage{amsmath, amsthm, amssymb, amsfonts}
tikzset{>=latex}begin{document}
begin{tikzpicture}node[circle, draw = black, fill = gray!20, inner sep = 0pt, minimum size = 0.65cm] (obs) at (0, 0) {{$y_{ijt}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (ui) at (-0.9, 0.9) {{$boldsymbol{u}_{i}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (vj) at (0, 1.8) {{$boldsymbol{v}_{j}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (xt) at (0.9, 0.95) {{$boldsymbol{x}_{t}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (phi) at (-0.9, -0.7) {{$phi_{i}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (theta) at (0, -2) {{$theta_{j}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (eta) at (0.9, -0.75) {{$eta_{t}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.55cm] (tau) at (2, 0) {{$tau$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.55cm] (mu) at (-2, 0) {{$mu$}};path [draw, ->] (ui) edge (obs);
path [draw, ->] (vj) edge (obs);
path [draw, ->] (xt) edge (obs);
path [draw, ->] (tau) edge (obs);
path [draw, ->] (mu) edge (obs);
path [draw, ->] (phi) edge (obs);
path [draw, ->] (theta) edge (obs);
path [draw, ->] (eta) edge (obs);node [text width = 0.2cm] (m) at (-1.1, 0.3) {small{$m$}};
plate[] {plate1} {(obs) (ui) (m) (phi)} { };
node [text width = 0.6cm] (n) at (0, -1.55) {small{$n$}};
plate[] {plate2} {(obs) (vj) (n) (theta)} { };
node [text width = 0.2cm] (f) at (1.1, 0.3) {small{$f$}};
plate[] {plate3} {(obs) (xt) (f) (eta)} { };end{tikzpicture}
end{document}

將這里的代碼復制并粘貼到所創建的overleaf項目中，即可得到部分觀測變量的元素集合示意圖。

1d74afd2e797be094670a71ed8c4189f.png
圖: 新增貝葉斯模型部分觀測變量的元素集合

5) 繪制超參數節點及其有向邊

在這里，超參數分為待估計超參數和底層超參數，待估計超參數顧名思義是一個變量，而底層超參數則是常量。對于待估計超參數，我們仍要像繪制模型參數一樣繪制它，而底層超參數則不需要帶有“圓圈”，不過需要注意的是，兩者都可以用node命令進行繪制。

documentclass[tikz, border = 0.1cm]{standalone}
usepackage{tikz}
usetikzlibrary{bayesnet}
usepackage{amsmath, amsthm, amssymb, amsfonts}
tikzset{>=latex}begin{document}
begin{tikzpicture}node[circle, draw = black, fill = gray!20, inner sep = 0pt, minimum size = 0.65cm] (obs) at (0, 0) {{$y_{ijt}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (ui) at (-0.9, 0.9) {{$boldsymbol{u}_{i}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (vj) at (0, 1.8) {{$boldsymbol{v}_{j}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (xt) at (0.9, 0.95) {{$boldsymbol{x}_{t}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (phi) at (-0.9, -0.7) {{$phi_{i}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (theta) at (0, -2) {{$theta_{j}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (eta) at (0.9, -0.75) {{$eta_{t}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.55cm] (tau) at (2, 0) {{$tau$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.55cm] (mu) at (-2, 0) {{$mu$}};path [draw, ->] (ui) edge (obs);
path [draw, ->] (vj) edge (obs);
path [draw, ->] (xt) edge (obs);
path [draw, ->] (tau) edge (obs);
path [draw, ->] (mu) edge (obs);
path [draw, ->] (phi) edge (obs);
path [draw, ->] (theta) edge (obs);
path [draw, ->] (eta) edge (obs);node [text width = 0.2cm] (m) at (-1.1, 0.3) {small{$m$}};
plate[] {plate1} {(obs) (ui) (m) (phi)} { };
node [text width = 0.6cm] (n) at (0, -1.55) {small{$n$}};
plate[] {plate2} {(obs) (vj) (n) (theta)} { };
node [text width = 0.2cm] (f) at (1.1, 0.3) {small{$f$}};
plate[] {plate3} {(obs) (xt) (f) (eta)} { };node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (muv) at (-0.6, 2.8) {small{$boldsymbol{mu}_{v}$}};
node[circle, draw = black, inner sep = 0pt, minimum size = 0.6cm] (lambdav) at (0.6, 2.8) {small{$Lambda_{v}$}};
node[text width = 0.8cm] (gamma) at (2, 0.8) {small{$a_0,b_0$}};
node[text width = 0.8cm] (hyper1) at (-2, 0.8) {small{$mu_{0},tau_{0}$}};
node[text width = 0.8cm] (hyper2) at (1.2, -2) {small{$mu_{0},tau_{0}$}};
node[text width = 0.8cm] (hyper3) at (2.1, -0.75) {small{$mu_{0},tau_{0}$}};
node[text width = 0.8cm] (hyper4) at (-2.1, -0.7) {small{$mu_{0},tau_{0}$}};
node[text width = 0.4cm] (mu0) at (-0.6, 3.6) {small{$boldsymbol{mu}_{0}$}};
node[text width = 0.9cm] (wnu0) at (0.6, 3.6) {small{$W_{0},nu_{0}$}};
node[text width = 0.6cm] (cdots1) at (-1, 1.6) {Largecolor{gray}{$cdots$}};
node[text width = 0.6cm] (cdots2) at (1, 1.6) {Largecolor{gray}{$cdots$}};path [draw, ->] (muv) edge (vj);
path [draw, ->] (lambdav) edge (vj);
path [draw, ->] (lambdav) edge (muv);
path [draw, ->] (mu0) edge (muv);
path [draw, ->] (wnu0) edge (lambdav);
path [draw, ->] (gamma) edge (tau);
path [draw, ->] (hyper1) edge (mu);
path [draw, ->] (hyper2) edge (theta);
path [draw, ->] (hyper3) edge (eta);
path [draw, ->] (hyper4) edge (phi);end{tikzpicture}
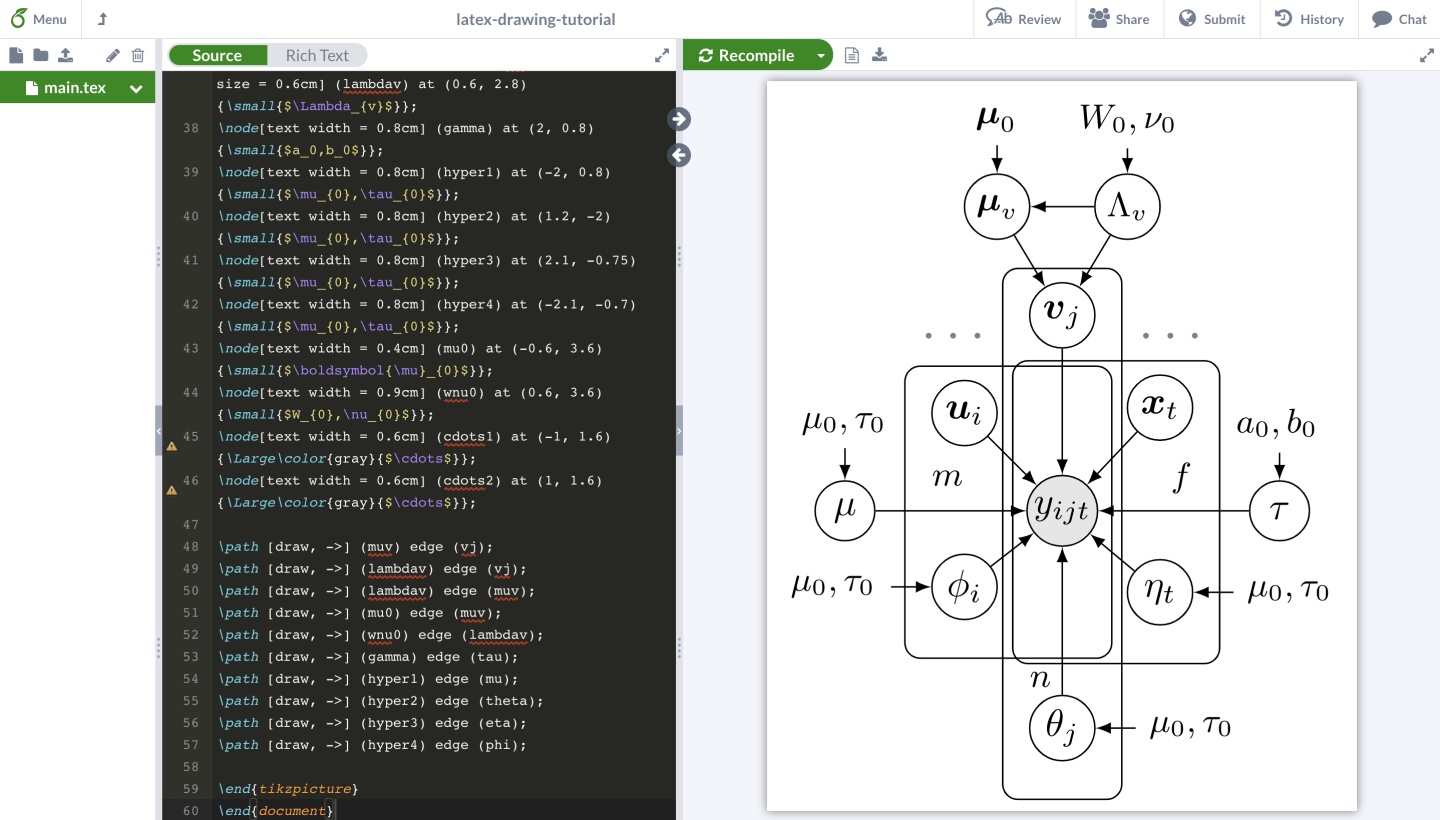
end{document}

將這里的代碼復制并粘貼到所創建的overleaf項目中，即可得到我們希望得到的包含了超參數節點及其有向邊的貝葉斯網絡結構圖。

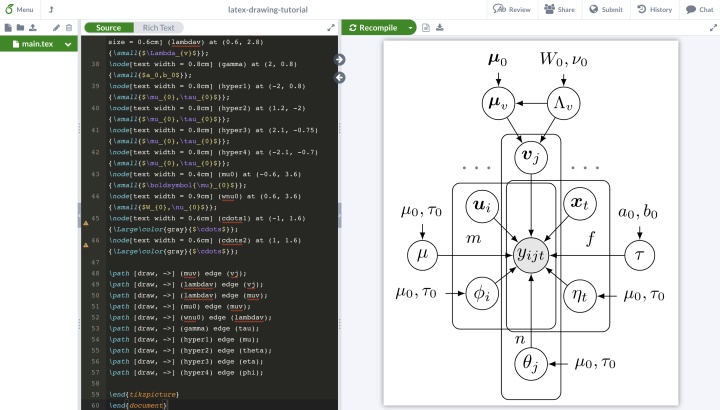
bf77bbd2b1513797de5acc8c6dbe992f.png
圖: 新增貝葉斯模型的超參數及其有向邊

到這里，我們便完成了完整的貝葉斯網絡繪制。

LaTeX相關入門學習材料：

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/532071.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/532071.shtml
英文地址，請注明出處：http://en.pswp.cn/news/532071.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

python123動物重量排序_python進階

python123動物重量排序_python進階

面向對象oopclass Student(object):def __init__(self,name,score)self.name nameself.score scoredef print_score(self)print(%s: %s % (self.name,self.score))給對象發消息實際上就是調用對象對應的關聯函數，我們稱之為對象的方法(Method)。面向對象的程序寫出…
閱讀更多...
mysql中的生日應該是什么類型_MySQL中的定點數類型

mysql中的生日應該是什么類型_MySQL中的定點數類型

上一篇文章我們嘮叨了浮點數，知道了浮點數存儲小數是不精確的。本篇繼續嘮叨一下MySQL中的另一種存儲小數的方式 —— 定點數。浮點數文章閃現：什么, 0.3 - 0.2 ≠ 0.1 ? 什么鬼定點數類型正因為用浮點數表示小數可能會有不精確的情況，在一些…
閱讀更多...
python怎么制作圖像_python數字圖像處理（5）：圖像的繪制

python怎么制作圖像_python數字圖像處理（5）：圖像的繪制

實際上前面我們就已經用到了圖像的繪制，如：io.imshow(img)這一行代碼的實質是利用matplotlib包對圖片進行繪制，繪制成功后，返回一個matplotlib類型的數據。因此，我們也可以這樣寫：importmatplotlib.pyplot …
閱讀更多...
axios代理跨域 cli4_vuecli 3.0之跨域請求代理配置及axios路徑配置 莫小龍

axios代理跨域 cli4_vuecli 3.0之跨域請求代理配置及axios路徑配置 莫小龍

vue-cli 3.0之跨域請求代理配置及axios路徑配置問題：在前后端分離的跨域請求中，報跨域問題配置：vue.config.js：module.exports {runtimeCompiler: true,publicPath: /, // 設置打包文件相對路徑devServer: {// open: process.pla…
閱讀更多...
string轉為char數組_StringBuilder的區別是什么？String是不可變？一點課堂(多岸學院)...

string轉為char數組_StringBuilder的區別是什么？String是不可變？一點課堂(多岸學院)...

String和StringBuffer、StringBuilder的區別可變性簡單的來說：String 類中使用 final 關鍵字字符數組保存字符串，private　final　char　value[]，所以 String 對象是不可變的。而StringBuilder 與 StringBuffer 都繼承自 AbstractStringBuild…
閱讀更多...
python去年軟件排行_2017年編程語言排行榜,Python位居榜首(C語言需求最大)

python去年軟件排行_2017年編程語言排行榜,Python位居榜首(C語言需求最大)

最近IEEE Spectrum 發布了編程語言交互式排行榜，為很多學習代碼的朋友們詳解各類代碼語言的需求和占有率。為學習代碼的朋友們能更加重視哪一種編程語言而有一個明確的方向。下面排行榜123網為你公布2017年編程語言排行榜,Python位居榜首(C語言需求最大)。2017年編程…
閱讀更多...
mysql test數據庫_mysql數據庫test

mysql test數據庫_mysql數據庫test

Re介紹一下CentOS下MySQL數據庫的安裝與配置方法MySQL數據庫配置的具體步驟：1、編輯MySQL的配置文件，使用vi /etc/my.cnf[rootsample ~]# vi /etc/my.cnf　 ← 編輯MySQL的配置文件[mysqld]datadir/var/lib/mysqlsocket/var/lib/mysql/mysql.sock# Defau…
閱讀更多...
mysql 升級 openssl_【1分鐘教程】LNMP架構應用實戰 Openssl升級操作

mysql 升級 openssl_【1分鐘教程】LNMP架構應用實戰 Openssl升級操作

由于實際生產環境需求，需要將LNMP環境中的openssl版本升級至目前最新版本openssl-1.1.0c，這玩意升級還真的不是一般的麻煩，由于它與系統各種服務都有相關的聯系，比如ssh服務等，因此，升級非常的繁瑣,所以今天…
閱讀更多...
miui秒解bl鎖_MIUI12解鎖bl篇（原諒我的過失，接上篇文章）

miui秒解bl鎖_MIUI12解鎖bl篇（原諒我的過失，接上篇文章）

求原諒真心求原諒由于我的疏忽，上期教程不完整，對大家造成不便在這里給大家真誠道歉！對不起！請收下我的膝蓋！！！我的上個教程小米手機MIUI系統降級任意版本通用教程，MIUI12→MIUI9因為…
閱讀更多...
腐蝕rust服務器命令_【使用 Rust 寫 Parser】2. 解析Redis協議

腐蝕rust服務器命令_【使用 Rust 寫 Parser】2. 解析Redis協議

系列所有文章https://zhuanlan.zhihu.com/p/115017849?zhuanlan.zhihu.comhttps://zhuanlan.zhihu.com/p/139387293?zhuanlan.zhihu.comhttps://zhuanlan.zhihu.com/p/146455601?zhuanlan.zhihu.comhttps://zhuanlan.zhihu.com/p/186217695?zhuanlan.zhihu.com在基本熟悉 n…
閱讀更多...
python中dic_python之dic {字典}(重要指數*****)

python中dic_python之dic {字典}(重要指數*****)

1. 什么是字典{name: 汪峰, age: 18} 鍵:值 別的語言鍵值對數據鍵: 必須是可哈希(不可變的數據類型),并且是唯一的值: 任意可以保存任意類型的數據字典是無序的python3.6版本以上,默認定義了順序,python3.5以下是隨機顯示不能進?切片?作. 它只能通過key來獲取dict中的數據字典…
閱讀更多...
python裝飾器帶參數函數二階導數公式_一文搞定Python裝飾器，看完面試不再慌

python裝飾器帶參數函數二階導數公式_一文搞定Python裝飾器，看完面試不再慌

本文始發于個人公眾號：TechFlow，原創不易，求個關注今天是Python專題的第12篇文章，我們來看看Python裝飾器。一段囧事差不多五年前面試的時候，我就領教過它的重要性。那時候我Python剛剛初學乍練，看完了廖雪…
閱讀更多...
centos7源碼安裝mysql報錯_CentOS7 下源碼安裝MySQL數據庫 8.0.11

centos7源碼安裝mysql報錯_CentOS7 下源碼安裝MySQL數據庫 8.0.11

本文主要向大家介紹了CentOS7 下源碼安裝MySQL數據庫 8.0.11，通過具體的內容向大家展現，希望對大家學習MySQL數據庫有所幫助。CentOS7 下源碼安裝MySQL 8.0.11系統環境：CentOS7， 內核：Linux 3.10.0-862.el7.x86_64如果…
閱讀更多...
python全排列問題_Python基于回溯法子集樹模板解決全排列問題示例

python全排列問題_Python基于回溯法子集樹模板解決全排列問題示例

本文實例講述了Python基于回溯法子集樹模板解決全排列問題。分享給大家供大家參考，具體如下：問題實現 a, b, c, d 四個元素的全排列。分析這個問題可以直接套用排列樹模板。不過本文使用子集樹模板。分析如下：一個解x就是n個元素的一種排列&a…
閱讀更多...
file js new 傳到后臺_js 圖片上傳傳給后臺的3種格式

file js new 傳到后臺_js 圖片上傳傳給后臺的3種格式

$("#imgfile").change(function () {var formData new FormData();$.each($(#imgfile)[0].files, function (i, file) {formData.set(idcard, file); //idcard 字段 根據自己后端接口定});//processData: false, contentType: false,多用來處理異步上傳二進制文件。…
閱讀更多...
usbserialcontroller驅動安裝不了_win10-有NVIDIA獨顯提示未安裝控制面板的離線安裝方式...

usbserialcontroller驅動安裝不了_win10-有NVIDIA獨顯提示未安裝控制面板的離線安裝方式...

最近越來越多的用戶反映NVIDIA顯卡驅動設置不了啦，找不到NVIDIA顯卡的控制面板。 也不知道NVIDIA在什么版本開始驅動安裝包就不自帶NVIDIA顯卡控制面板了。 全新安裝的顯卡驅動就沒有控制面板；或者Windows 10自帶更新了顯卡新版驅動后導致沒有。 每次帶N…
閱讀更多...
mysql 多實例 獨立配置文件_三、安裝配置多實例MYSQL5.6-多獨立配置文件方法

mysql 多實例 獨立配置文件_三、安裝配置多實例MYSQL5.6-多獨立配置文件方法

三、安裝配置多實例MYSQL5.6-多獨立配置文件方法1、準備工作檢查操作系統版本、內核版本、selinux是否關閉、防火墻策略、IP地址、主機名配置、host表配置、yum配置上傳cmake、mysql5.6軟件包具體步驟參考源碼安裝mysql-單實例配置文檔2、安裝cmake軟件2.1 安裝編譯軟件環境[[e…
閱讀更多...
python做什么模型_主題模型初學者指南[Python]

python做什么模型_主題模型初學者指南[Python]

引言近年來涌現出越來越多的非結構化數據，我們很難直接利用傳統的分析方法從這些數據中獲得信息。但是新技術的出現使得我們可以從這些輕易地解析非結構化數據，并提取出重要信息。主題模型是處理非結構化數據的一種常用方法，從名字中就可以看…
閱讀更多...
python實現隊列_Python學習教程：用隊列實現棧

python實現隊列_Python學習教程：用隊列實現棧

接著上一期跟大家說的用棧實現隊列，這期的Python學習教程跟大家講用隊列實現棧題目：使用隊列實現棧的下列操作：push(x) – 元素 x 入棧pop() – 移除棧頂元素top() – 獲取棧頂元素empty() – 返回棧是否為空Implement the following operati…
閱讀更多...
vue 點擊li 中的img 怎么不冒泡_Vue全解

vue 點擊li 中的img 怎么不冒泡_Vue全解

一.Vue實例內存圖：1.把Vue的實例命名為vm，vm對象封裝了對視圖的所有操作包括數據讀寫、事件綁定、DOM更新2.vm的構造函數是Vue，按照ES6的說法vm所屬的類是Vue3.options是new Vue的參數一般稱為選項或構造選項1.options里面有什么英文文檔搜op…
閱讀更多...
最新文章

Copyright @ 2022~2023