平衡二叉樹(Balancedbinary tree)是由阿德爾森-維爾斯和蘭迪斯(Adelson-Velskiiand Landis)于1962年首先提出的,所以又稱為AVL樹。
定義:平衡二叉樹或為空樹,或為如下性質的二叉排序樹:
?(1)左右子樹深度之差的絕對值不超過1;
?(2)左右子樹仍然為平衡二叉樹.
??????? 平衡二叉樹可以避免排序二叉樹深度上的極度惡化,使樹的高度維持在O(logn)來提高檢索效率。
?
因為插入節點導致整個二叉樹失去平衡分成如下的四種情況:

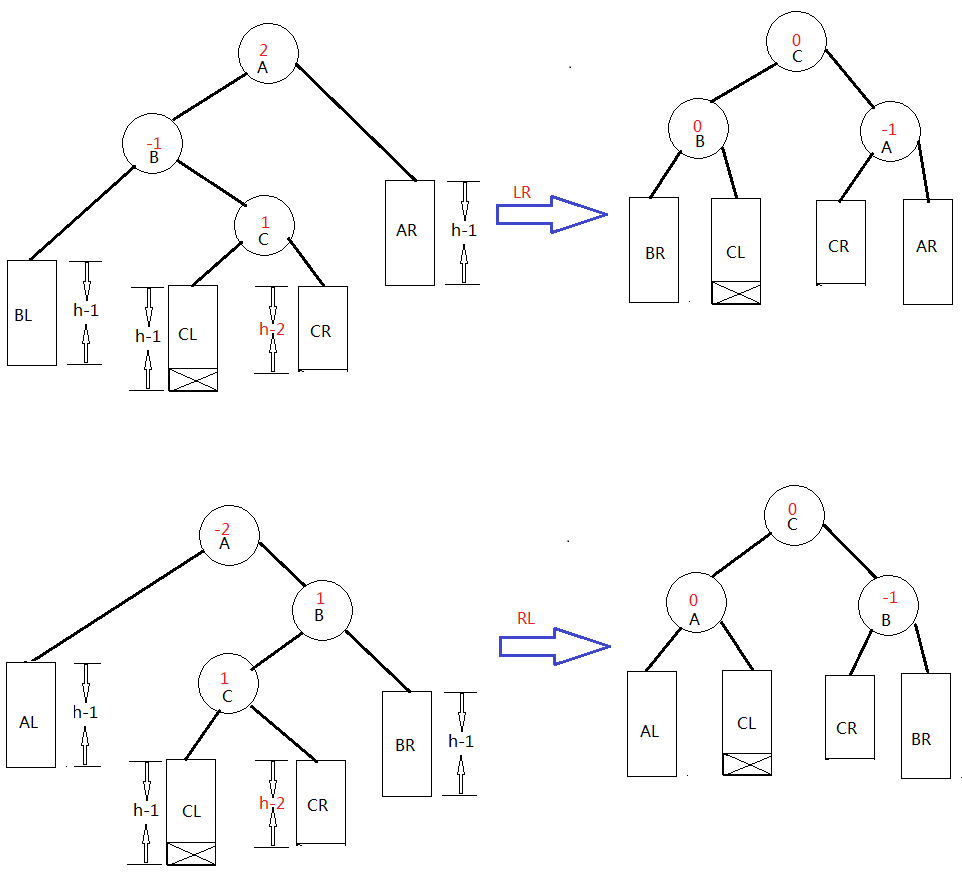
假設由于在二叉排序樹上插入節點而失去平衡的最小子數根節點的指針為a(即a是離插入節點最近,且平衡因子絕對值超過1的祖先節點),則失去平衡后進行調整的規律如下:
1.如上圖LL單向右旋處理:由于在*a的左子樹根節點的左子樹上插入節點,*a的平衡因子由1增至2,致使以*a為根節點的子樹失去平衡,則需要進行一次向右的順時針旋轉操作。
2.如上圖RR單向左旋處理:由于在*a的右子樹根節點的右子樹上插入節點, *a的平衡因子有-1變為-2,致使以*a為根節點的子樹失去平衡,則學要進行一次向左的逆時針旋轉操作。
3.如上圖LR雙向旋轉(先左后右)處理:由于在*a的左子樹根節點的右子樹插入節點,*a的平衡因子有1增至2,致使以*a為根節點的子樹失去平衡,則需要進行兩次旋轉(先左旋后右旋)操作。
4.如上圖RL雙向旋轉(先右后左)處理:由于在*a的右子樹根節點的左子樹上插入節點,*a的平衡因子由-1變為-2,致使以*a為根節點的子樹失去平衡,則需要進行兩次旋轉(先左旋后右旋)操作。
#include<iostream> #include<cstring> #include<string> #include<queue> #include<map> #include<cstdio> #define LH 1 //左高 #define EH 0 //等高 #define RH -1 //右高 using namespace std;template <typename ElemType> class BSTNode{public:ElemType data;//節點的數據 int bf;//節點的平衡因子BSTNode *child[2];BSTNode(){child[0] = NULL;child[1] = NULL;} };typedef BSTNode<string> BSTnode, *BSTree;template <typename ElemType> class AVL{public:BSTNode<ElemType> *T;void buildT();void outT(BSTNode<ElemType> *T);private:bool insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller); void rotateT(BSTNode<ElemType>* &o, int x);//子樹的左旋或者右旋void leftBalance(BSTNode<ElemType>* &o);void rightBalance(BSTNode<ElemType>* &o); };template <typename ElemType> void AVL<ElemType>::rotateT(BSTNode<ElemType>* &o, int x){BSTNode<ElemType>* k = o->child[x^1];o->child[x^1] = k->child[x];k->child[x] = o;o = k; }template <typename ElemType> void AVL<ElemType>::outT(BSTNode<ElemType> *T){if(!T) return;cout<<T->data<<" ";outT(T->child[0]);outT(T->child[1]); }template <typename ElemType> void AVL<ElemType>::buildT(){T = NULL;ElemType key;while(cin>>key){if(key==0) break;bool taller = false;insertAVL(T, key, taller);outT(T);cout<<endl;} }template <typename ElemType> bool AVL<ElemType>::insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller){if(!T){//插入新的節點,taller=true 那么樹的高度增加 T = new BSTNode<ElemType>();T->data = key;T->bf = EH;taller = true;} else {if(T->data == key){taller = false;return false;}if(T->data > key){//向T的左子樹進行搜索并插入 if(!insertAVL(T->child[0], key, taller)) return false;if(taller){// switch(T->bf){case LH://此時左子樹的高度高,左子樹上又插入了一個節點,失衡,需要進行調整 leftBalance(T);taller = false;//調整之后高度平衡 break; case EH:T->bf = LH;taller = true;break; case RH:T->bf = EH;taller = false; break;}}} if(T->data < key) {//向T的右子樹進行搜索并插入 if(!insertAVL(T->child[1], key, taller)) return false;switch(T->bf){case LH:T->bf = EH;taller = false; break; case EH:T->bf = RH;taller = true;break; case RH:rightBalance(T); taller = false; break;}}}return true; }template <typename ElemType> void AVL<ElemType>::leftBalance(BSTNode<ElemType>* &T){BSTNode<ElemType>* lchild = T->child[0];switch(lchild->bf){//檢查T的左子樹的平衡度,并作相應的平衡處理 case LH://新節點 插入到 T的左孩子的左子樹上,需要對T節點做單旋(右旋)處理 T->bf = lchild->bf = EH; rotateT(T, 1);break;case RH://新節點 插入到 T的左孩子的右子樹上,需要做雙旋處理 1.對lchild節點進行左旋,2.對T節點進行右旋 BSTNode<ElemType>* rdchild = lchild->child[1];switch(rdchild->bf){//修改 T 及其左孩子的平衡因子 case LH: T->bf = RH; lchild->bf = EH; break;case EH: T->bf = lchild->bf = EH; break;//發生這種情況只能是 rdchild無孩子節點case RH: T->bf = EH; lchild->bf = LH; break; }rdchild->bf = EH; rotateT(T->child[0], 0);//不要寫成 rotateT(lc, 0);//這樣的話T->lchild不會改變 rotateT(T, 1);break;} }template <typename ElemType> void AVL<ElemType>::rightBalance(BSTNode<ElemType>* &T){BSTNode<ElemType>* rchild = T->child[1];switch(rchild->bf){//檢查T的左子樹的平衡度,并作相應的平衡處理 case RH://新節點 插入到 T的右孩子的右子樹上,需要對T節點做單旋(左旋)處理 T->bf = rchild->bf = EH; rotateT(T, 0);break;case LH://新節點 插入到 T的右孩子的左子樹上,需要做雙旋處理 1.對rchild節點進行右旋,2.對T節點進行左旋 BSTNode<ElemType>* ldchild = rchild->child[0];switch(ldchild->bf){//修改 T 及其右孩子的平衡因子 case LH: T->bf = EH; rchild->bf = RH; break;case EH: T->bf = rchild->bf = EH; break;//發生這種情況只能是 ldchild無孩子節點 case RH: T->bf = LH; rchild->bf = EH; break; }ldchild->bf = EH; rotateT(T->child[1], 1);rotateT(T, 0);break;} }int main(){AVL<int> avl;avl.buildT();avl.outT(avl.T);return 0; } /*13 24 37 90 53 0 */
?
)
C語言之二維數組)

C語言之函數)

C語言之指針)
)
C語言之結構)



)







