數值作業:龍貝格算法計算積分C語言實現
數值作業:龍貝格算法計算積分C語言實現
根據Romberg算法計算定積分,和變步長的Simpson算法的輸入都一樣.算法基本分析:輸入a,b(積分上下限),n為積分區間等分數,eps為計算精度,我這里1e-7,代表0乘以10的負7次方.本題目取的例子為數值書137面的例子2,f(x)= sin(x)/x,下面給出代碼:
/********************************************
> File Name: Dragon.c
> Author:chendiyang
> School:WUST_CST_1501班
> Myblog:www.chendsir.com
> Mail:[email?protected]
> Created Time: 2017年05月6日 星期六 12時33分10秒
************************************************************************/
#include
#include
#define N 20
#define MAX 10 //數組存的最大行數
#define a 0.0000001 //積分下限
#define b 1.0 //積分上限
#define eps 1e-7 //精度
double f(double x)//所求積分公式
{
return sin(x) / x;
}
double computeT(double aa, double bb, long int n)//復化梯形公式
{
int i;
double sum, h = (bb - aa) / n;
for (i = 1; i < n; i++)
sum += f(aa + i * h);
sum += (f(aa) + f(bb)) / 2;
return (h * sum);
}
double f2(double x)
{
return x*x;
}
int main()
{
int i;
long int n = N,m = 0;
double T[MAX + 1][2];
T[0][1]=computeT(a,b,n);
n*= 2;
for (m = 1; m < MAX; m++)
{
for (i = 0; i < m; i++)
{
T[i][0] = T[i][1];
}
T[0][1]=computeT(a,b,n);
n *= 2;
for (i = 1; i <= m; i++) //T的m(h)
T[i][1] = T[i - 1][1] + (T[i - 1][1] - T[i - 1][0]) / (pow(2, 2 * m) - 1);
if ((T[m - 1][1] < T[m][1] + eps) && (T[m - 1][1] > T[m][1] - eps))
{
printf("計算的數為:%lf\n", T[m][1]); //輸出
return 0;
}
}
printf("此題沒有解...\n");
return 0;
}
運行結果:
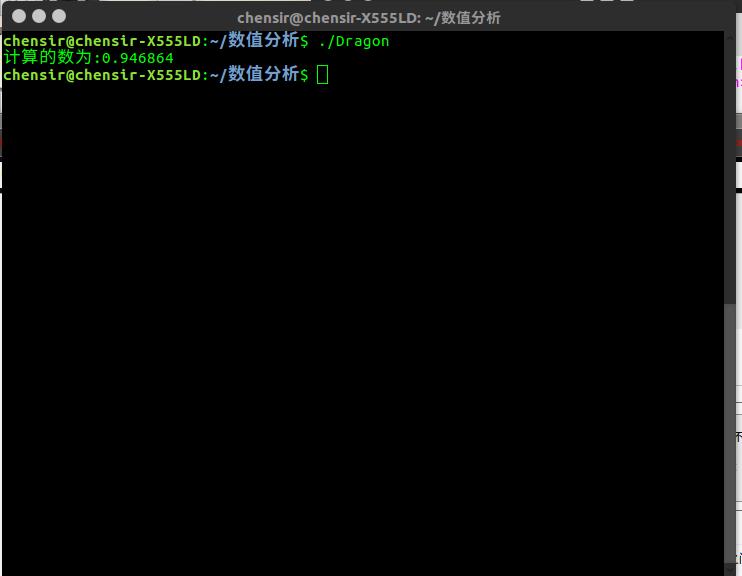
可見計算的結果是正確的,然而中間因為一個小小的中文空格替換問題,調試了整整一小時,等發現錯在哪之后,才拍大腿,恍然大悟,腦子一直在想我TM到底錯在哪了.雖然煩,以前一位學長說程序員們基本都是吾日三省吾身的,每當Debug的時候,感觸最深..
紙上得來終覺淺,絕知此事需躬行.
數值作業:龍貝格算法計算積分C語言實現相關教程









)









中,“:hover”樣式的設置問題?)