from:https://blog.csdn.net/jia20003/article/details/53021614
圖像處理之積分圖應用三(基于NCC快速相似度匹配算法)
基于Normalized cross correlation(NCC)用來比較兩幅圖像的相似程度已經是一個常見的圖像處理手段。在工業生產環節檢測、監控領域對對象檢測與識別均有應用。NCC算法可以有效降低光照對圖像比較結果的影響。而且NCC最終結果在0到1之間,所以特別容易量化比較結果,只要給出一個閾值就可以判斷結果的好與壞。傳統的NCC比較方法比較耗時,雖然可以通過調整窗口大小和每次檢測的步長矩形部分優化,但是對工業生產檢測然后不能達到實時需求,通過積分圖像實現預計算,比較模板圖像與生產出電子版之間的細微差異,可以幫助企業提高產品質量,減少次品出廠率,把控質量。
一:NCC相關的數學知識
什么是NCC - (normalized cross correlation)歸一化的交叉相關性,是數學上統計兩組數據之間是否有關系的判斷方法,貌似搞大數據分析比較流行相關性分析和計算。正常的計算公式如下:
mxn表示窗口大小,這樣的計算復雜度就為O(m x n x M x N)。從上面公式就可以看出其中均值和平方和可以通過積分圖預計算得到,對于模板和目標圖像大小一致的應用場景來說
NCC的計算公式可以表示為如下:
其中根據積分圖像可以提前計算出任意窗口大小和與平方和,這樣就對
上述兩個計算實現了窗口半徑無關的常量時間計算,唯一缺少的是下面計算公式
通過積分圖像建立起來窗口下面的待檢測圖像與模板圖像的和與平方和以及他們的交叉乘積五個積分圖索引之后,這樣就完成了整個預計算生成。依靠索引表查找計算結果,NCC就可以實現線性時間的復雜度計算,而且時間消耗近似常量跟窗口半徑大小無關,完全可以滿足實時對象檢測工業環境工作條件。
?
二:算法步驟
1. 預計算模板圖像和目標圖像的積分圖
2. 根據輸入的窗口半徑大小使用積分圖完成NCC計算
3. 根據閾值得到匹配或者不匹配區域。
4. 輸出結果
為了減小計算量,我們可以要把輸入的圖像轉換為灰度圖像,在灰度圖像的基礎上完成整個NCC計算檢測。我們這個給出的基于RGB圖像的NCC計算完整代碼,讀者可以在此基礎上修改實現單通道圖像檢測。
三: 運行結果:
輸入的模板圖像與待檢測圖像,左邊是模板圖像,右邊是待檢測圖像,左上角有明顯污點。圖像顯示如下:
??
輸入待檢測圖像與模板比較以及檢測計算出NCC的圖像顯示如下:
其中左側是待檢測圖像,上面有黑色污點,右側輸出的非黑色區域表明,程序已經發現此區域與標準模板不同,越白的區域表示周圍跟模板相同位置反差越大,越是可疑的污染點,這樣就可以得到準確定位,最終帶檢測圖像繪制最可疑紅色矩形窗口區域
四:相關代碼實現
1. 計算兩張圖像每個像素交叉乘積的積分圖代碼如下:
public void caculateXYSum(byte[] x, byte[] y, int width, int height) {if(x.length != y.length)return;xysum = new float[width*height];this.width = width;this.height = height;// rowsint px = 0, py = 0;int offset = 0, uprow=0, leftcol=0;float sp2=0, sp3=0, sp4=0;for(int row=0; row<height; row++ ) {offset = row*width;uprow = row-1;for(int col=0; col<width; col++) {leftcol=col-1;px=x[offset]&0xff;py=y[offset]&0xff;int p1 = px*py;// 計算平方查找表sp2=(leftcol<0) ? 0:xysum[offset-1]; // p(x-1, y)sp3=(uprow<0) ? 0:xysum[offset-width]; // p(x, y-1);sp4=(uprow<0||leftcol<0) ? 0:xysum[offset-width-1]; // p(x-1, y-1);xysum[offset]=p1+sp2+sp3-sp4;offset++;}}}
獲取任意窗口大小的交叉乘積的代碼如下:
public float getXYBlockSum(int x, int y, int m, int n) {int swx = x + n/2;int swy = y + m/2;int nex = x-n/2-1;int ney = y-m/2-1;float sum1, sum2, sum3, sum4;if(swx >= width) {swx = width - 1;}if(swy >= height) {swy = height - 1;}if(nex < 0) {nex = 0;}if(ney < 0) {ney = 0;}sum1 = xysum[ney*width+nex];sum4 = xysum[swy*width+swx];sum2 = xysum[swy*width+nex];sum3 = xysum[ney*width+swx];return ((sum1 + sum4) - sum2 - sum3);}
?
其余部分的積分圖計算,參見本人博客《圖像處理之積分圖算法》
2. 預計算建立積分圖索引的代碼如下:
// per-calculate integral image for targetImagebyte[] R = new byte[width * height];byte[] G = new byte[width * height];byte[] B = new byte[width * height];getRGB(width, height, pixels, R, G, B);IntIntegralImage rii = new IntIntegralImage();rii.setImage(R);rii.process(width, height);IntIntegralImage gii = new IntIntegralImage();gii.setImage(G);gii.process(width, height);IntIntegralImage bii = new IntIntegralImage();bii.setImage(B);bii.process(width, height);// setup the refer and target image index sum tablerii.caculateXYSum(R, referRGB[0].getImage(), width, height);gii.caculateXYSum(G, referRGB[1].getImage(), width, height);bii.caculateXYSum(B, referRGB[2].getImage(), width, height);int size = (xr * 2 + 1) * (yr * 2 + 1);
3. 通過積分圖查找實現快速NCC計算的代碼如下:
int r1=0, g1=0, b1=0;int r2=0, g2=0, b2=0;float sr1=0.0f, sg1=0.0f, sb1 = 0.0f;float sr2=0.0f, sg2=0.0f, sb2 = 0.0f;float xyr = 0.0f, xyg = 0.0f, xyb = 0.0f;for (int row = yr; row < height - yr; row++) {for (int col = xr; col < width - xr; col++) {r1 = rii.getBlockSum(col, row, (yr * 2 + 1), (xr * 2 + 1));g1 = gii.getBlockSum(col, row, (yr * 2 + 1), (xr * 2 + 1));b1 = bii.getBlockSum(col, row, (yr * 2 + 1), (xr * 2 + 1));r2 = referRGB[0].getBlockSum(col, row, (yr * 2 + 1), (xr * 2 + 1));g2 = referRGB[1].getBlockSum(col, row, (yr * 2 + 1), (xr * 2 + 1));b2 = referRGB[2].getBlockSum(col, row, (yr * 2 + 1), (xr * 2 + 1));sr1 = rii.getBlockSquareSum(col, row, (yr * 2 + 1), (xr * 2 + 1));sg1 = gii.getBlockSquareSum(col, row, (yr * 2 + 1), (xr * 2 + 1));sb1 = bii.getBlockSquareSum(col, row, (yr * 2 + 1), (xr * 2 + 1));sr2 = referRGB[0].getBlockSquareSum(col, row, (yr * 2 + 1), (xr * 2 + 1));sg2 = referRGB[1].getBlockSquareSum(col, row, (yr * 2 + 1), (xr * 2 + 1));sb2 = referRGB[2].getBlockSquareSum(col, row, (yr * 2 + 1), (xr * 2 + 1));xyr = rii.getXYBlockSum(col, row, (yr * 2 + 1), (xr * 2 + 1));xyg = gii.getXYBlockSum(col, row, (yr * 2 + 1), (xr * 2 + 1));xyb = bii.getXYBlockSum(col, row, (yr * 2 + 1), (xr * 2 + 1));float nccr = calculateNCC(r1, r2, sr1, sr2, xyr, size);float nccg = calculateNCC(g1, g2, sg1, sg2, xyg, size);float nccb = calculateNCC(b1, b2, sb1, sb2, xyb, size);outPixels[row * width + col] = (nccr + nccg + nccb);}}System.out.println("time consum : " + (System.currentTimeMillis() - time));
4. 歸一化輸出NCC圖像與結果代碼如下:
// normalization the datafloat max = 0.0f, min = 100.0f;for(int i=0; i<outPixels.length; i++) {max = Math.max(max, outPixels[i]);min = Math.min(min, outPixels[i]);}// create output image float delta = max - min;BufferedImage bi = new BufferedImage(width, height, BufferedImage.TYPE_INT_ARGB);int ry = -1;int rx = -1;for(int row = 0; row<height; row++) {for(int col=0; col<width; col++) {int gray = (int)(((outPixels[row*width+col]-min) / delta) *255);gray = 255 - gray;if(min == outPixels[row*width+col]) {bi.setRGB(col, row, Color.RED.getRGB());ry = row;rx = col;} else {int color = (0xff << 24) | (gray << 16) | (gray << 8) | gray;bi.setRGB(col, row, color);}}}if(rx > 0 && ry > 0) {Graphics2D g2d = image.createGraphics();g2d.setPaint(Color.RED);g2d.drawRect(rx-xr, ry-yr, xr*2, yr*2);}
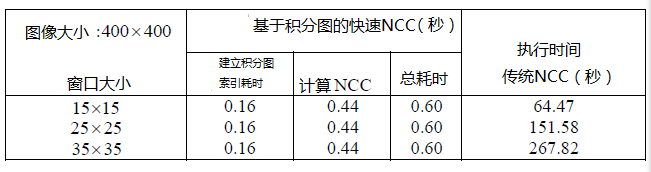
相比傳統的NCC計算方法,此方法的計算效率是傳統方法幾百倍提升,而且窗口越大效率提升越明顯,有人對此作出的統計如下:
可見基于積分圖快速NCC可以極大提升執行效率減少計算時間,實現窗口半徑無關NCC比較。
最后
本文是關于積分圖使用的第三篇文章,可以說積分圖在實際圖像處理中應用十分廣泛,本人會繼續努力深挖與大家分享。希望各位頂下次文以表支持, 謝謝!本人堅持分享有用實用的圖像處理算法!需要大家多多支持。
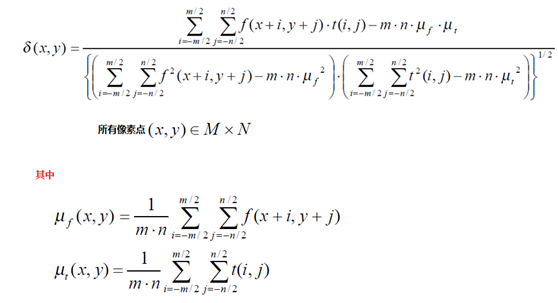

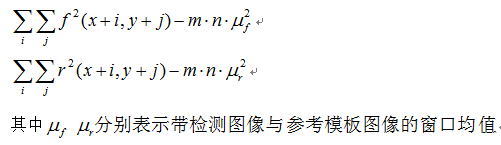
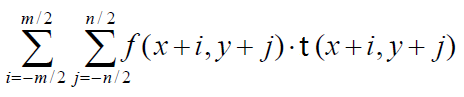





識別與分類)
)







-支持向量機(SVM)基礎)

 和KKT條件)

)


