from:http://www.cnblogs.com/LeftNotEasy/archive/2011/05/18/2034566.html
版權聲明:
??? 本文由LeftNotEasy發布于http://leftnoteasy.cnblogs.com, 本文可以被全部的轉載或者部分使用,但請注明出處,如果有問題,請聯系wheeleast@gmail.com。也可以加我的微博:?@leftnoteasy
?
前言:
??? 又有很長的一段時間沒有更新博客了,距離上次更新已經有兩個月的時間了。其中一個很大的原因是,不知道寫什么好-_-,最近一段時間看了看關于SVM(Support Vector Machine)的文章,覺得SVM是一個非常有趣,而且自成一派的方向,所以今天準備寫一篇關于關于SVM的文章。
??? 關于SVM的論文、書籍都非常的多,引用強哥的話“SVM是讓應用數學家真正得到應用的一種算法”。SVM對于大部分的普通人來說,要完全理解其中的數學是非常困難的,所以要讓這些普通人理解,得要把里面的數學知識用簡單的語言去講解才行。而且想明白了這些數學,對學習其他的內容也是大有裨益的。我就是屬于絕大多數的普通人,為了看明白SVM,看了不少的資料,這里把我的心得分享分享。
??? 其實現在能夠找到的,關于SVM的中文資料已經不少了,不過個人覺得,每個人的理解都不太一樣,所以還是決定寫一寫,一些雷同的地方肯定是不可避免的,不過還是希望能夠寫出一點與別人不一樣的地方吧。另外本文準備不談太多的數學(因為很多文章都談過了),盡量簡單地給出結論,就像題目一樣-機器學習中的算法(之前叫做機器學習中的數學),所以本系列的內容將更偏重應用一些。如果想看更詳細的數學解釋,可以看看參考文獻中的資料。
?
一、線性分類器:
????首先給出一個非常非常簡單的分類問題(線性可分),我們要用一條直線,將下圖中黑色的點和白色的點分開,很顯然,圖上的這條直線就是我們要求的直線之一(可以有無數條這樣的直線)
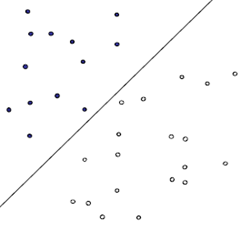 ??? 假如說,我們令黑色的點 = -1, 白色的點 =? +1,直線f(x) = w.x + b,這兒的x、w是向量,其實寫成這種形式也是等價的f(x) = w1x1 + w2x2 … + wnxn + b, 當向量x的維度=2的時候,f(x) 表示二維空間中的一條直線, 當x的維度=3的時候,f(x) 表示3維空間中的一個平面,當x的維度=n > 3的時候,表示n維空間中的n-1維超平面。這些都是比較基礎的內容,如果不太清楚,可能需要復習一下微積分、線性代數的內容。
??? 假如說,我們令黑色的點 = -1, 白色的點 =? +1,直線f(x) = w.x + b,這兒的x、w是向量,其實寫成這種形式也是等價的f(x) = w1x1 + w2x2 … + wnxn + b, 當向量x的維度=2的時候,f(x) 表示二維空間中的一條直線, 當x的維度=3的時候,f(x) 表示3維空間中的一個平面,當x的維度=n > 3的時候,表示n維空間中的n-1維超平面。這些都是比較基礎的內容,如果不太清楚,可能需要復習一下微積分、線性代數的內容。
??? 剛剛說了,我們令黑色白色兩類的點分別為+1, -1,所以當有一個新的點x需要預測屬于哪個分類的時候,我們用sgn(f(x)),就可以預測了,sgn表示符號函數,當f(x) > 0的時候,sgn(f(x)) = +1, 當f(x) < 0的時候sgn(f(x)) = –1。
??? 但是,我們怎樣才能取得一個最優的劃分直線f(x)呢?下圖的直線表示幾條可能的f(x)

??? 一個很直觀的感受是,讓這條直線到給定樣本中最近的點最遠,這句話讀起來比較拗口,下面給出幾個圖,來說明一下:
??? 第一種分法:

??? 第二種分法:

??? 這兩種分法哪種更好呢?從直觀上來說,就是分割的間隙越大越好,把兩個類別的點分得越開越好。就像我們平時判斷一個人是男還是女,就是很難出現分錯的情況,這就是男、女兩個類別之間的間隙非常的大導致的,讓我們可以更準確的進行分類。在SVM中,稱為Maximum Marginal,是SVM的一個理論基礎之一。選擇使得間隙最大的函數作為分割平面是由很多道理的,比如說從概率的角度上來說,就是使得置信度最小的點置信度最大(聽起來很拗口),從實踐的角度來說,這樣的效果非常好,等等。這里就不展開講,作為一個結論就ok了,:)
??? 上圖被紅色和藍色的線圈出來的點就是所謂的支持向量(support vector)。
?? ??? 上圖就是一個對之前說的類別中的間隙的一個描述。Classifier Boundary就是f(x),紅色和藍色的線(plus plane與minus plane)就是support vector所在的面,紅色、藍色線之間的間隙就是我們要最大化的分類間的間隙。
??? 上圖就是一個對之前說的類別中的間隙的一個描述。Classifier Boundary就是f(x),紅色和藍色的線(plus plane與minus plane)就是support vector所在的面,紅色、藍色線之間的間隙就是我們要最大化的分類間的間隙。
??? 這里直接給出M的式子:(從高中的解析幾何就可以很容易的得到了,也可以參考后面Moore的ppt)

??? 另外支持向量位于wx + b = 1與wx + b = -1的直線上,我們在前面乘上一個該點所屬的類別y(還記得嗎?y不是+1就是-1),就可以得到支持向量的表達式為:y(wx + b) = 1,這樣就可以更簡單的將支持向量表示出來了。
??? 當支持向量確定下來的時候,分割函數就確定下來了,兩個問題是等價的。得到支持向量,還有一個作用是,讓支持向量后方那些點就不用參與計算了。這點在后面將會更詳細的講講。
??? 在這個小節的最后,給出我們要優化求解的表達式:
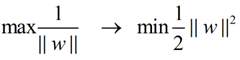
??? ||w||的意思是w的二范數,跟上面的M表達式的分母是一個意思,之前得到,M = 2 / ||w||,最大化這個式子等價于最小化||w||, 另外由于||w||是一個單調函數,我們可以對其加入平方,和前面的系數,熟悉的同學應該很容易就看出來了,這個式子是為了方便求導。
??? 這個式子有還有一些限制條件,完整的寫下來,應該是這樣的:(原問題)
![]()
??? s.t的意思是subject to,也就是在后面這個限制條件下的意思,這個詞在svm的論文里面非常容易見到。這個其實是一個帶約束的二次規劃(quadratic programming, QP)問題,是一個凸問題,凸問題就是指的不會有局部最優解,可以想象一個漏斗,不管我們開始的時候將一個小球放在漏斗的什么位置,這個小球最終一定可以掉出漏斗,也就是得到全局最優解。s.t.后面的限制條件可以看做是一個凸多面體,我們要做的就是在這個凸多面體中找到最優解。這些問題這里不展開,因為展開的話,一本書也寫不完。如果有疑問請看看wikipedia。
?
二、轉化為對偶問題,并優化求解:
??? 這個優化問題可以用拉格朗日乘子法去解,使用了KKT條件的理論,這里直接作出這個式子的拉格朗日目標函數:

??? 求解這個式子的過程需要拉格朗日對偶性的相關知識(另外pluskid也有一篇文章專門講這個問題),并且有一定的公式推導,如果不感興趣,可以直接跳到后面用藍色公式表示的結論,該部分推導主要參考自plukids的文章。
??? 首先讓L關于w,b最小化,分別令L關于w,b的偏導數為0,得到關于原問題的一個表達式
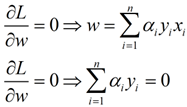
??? 將兩式帶回L(w,b,a)得到對偶問題的表達式

??? 新問題加上其限制條件是(對偶問題):
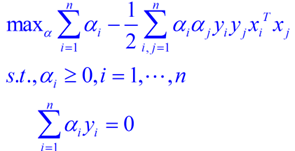
??? 這個就是我們需要最終優化的式子。至此,得到了線性可分問題的優化式子。
??? 求解這個式子,有很多的方法,比如SMO等等,個人認為,求解這樣的一個帶約束的凸優化問題與得到這個凸優化問題是比較獨立的兩件事情,所以在這篇文章中準備完全不涉及如何求解這個話題,如果之后有時間可以補上一篇文章來談談:)。
?
三、線性不可分的情況(軟間隔):
??? 接下來談談線性不可分的情況,因為線性可分這種假設實在是太有局限性了:
??? 下圖就是一個典型的線性不可分的分類圖,我們沒有辦法用一條直線去將其分成兩個區域,每個區域只包含一種顏色的點。
 ???? 要想在這種情況下的分類器,有兩種方式,一種是用曲線去將其完全分開,曲線就是一種非線性的情況,跟之后將談到的核函數有一定的關系:
???? 要想在這種情況下的分類器,有兩種方式,一種是用曲線去將其完全分開,曲線就是一種非線性的情況,跟之后將談到的核函數有一定的關系:
 ?????另外一種還是用直線,不過不用去保證可分性,就是包容那些分錯的情況,不過我們得加入懲罰函數,使得點分錯的情況越合理越好。其實在很多時候,不是在訓練的時候分類函數越完美越好,因為訓練函數中有些數據本來就是噪聲,可能就是在人工加上分類標簽的時候加錯了,如果我們在訓練(學習)的時候把這些錯誤的點學習到了,那么模型在下次碰到這些錯誤情況的時候就難免出錯了(假如老師給你講課的時候,某個知識點講錯了,你還信以為真了,那么在考試的時候就難免出錯)。這種學習的時候學到了“噪聲”的過程就是一個過擬合(over-fitting),這在機器學習中是一個大忌,我們寧愿少學一些內容,也堅決杜絕多學一些錯誤的知識。還是回到主題,用直線怎么去分割線性不可分的點:
?????另外一種還是用直線,不過不用去保證可分性,就是包容那些分錯的情況,不過我們得加入懲罰函數,使得點分錯的情況越合理越好。其實在很多時候,不是在訓練的時候分類函數越完美越好,因為訓練函數中有些數據本來就是噪聲,可能就是在人工加上分類標簽的時候加錯了,如果我們在訓練(學習)的時候把這些錯誤的點學習到了,那么模型在下次碰到這些錯誤情況的時候就難免出錯了(假如老師給你講課的時候,某個知識點講錯了,你還信以為真了,那么在考試的時候就難免出錯)。這種學習的時候學到了“噪聲”的過程就是一個過擬合(over-fitting),這在機器學習中是一個大忌,我們寧愿少學一些內容,也堅決杜絕多學一些錯誤的知識。還是回到主題,用直線怎么去分割線性不可分的點:
???? 我們可以為分錯的點加上一點懲罰,對一個分錯的點的懲罰函數就是這個點到其正確位置的距離:

?
??? 在上圖中,藍色、紅色的直線分別為支持向量所在的邊界,綠色的線為決策函數,那些紫色的線表示分錯的點到其相應的決策面的距離,這樣我們可以在原函數上面加上一個懲罰函數,并且帶上其限制條件為:
![]()
??? 公式中藍色的部分為在線性可分問題的基礎上加上的懲罰函數部分,當xi在正確一邊的時候,ε=0,R為全部的點的數目,C是一個由用戶去指定的系數,表示對分錯的點加入多少的懲罰,當C很大的時候,分錯的點就會更少,但是過擬合的情況可能會比較嚴重,當C很小的時候,分錯的點可能會很多,不過可能由此得到的模型也會不太正確,所以如何選擇C是有很多學問的,不過在大部分情況下就是通過經驗嘗試得到的。
??? 接下來就是同樣的,求解一個拉格朗日對偶問題,得到一個原問題的對偶問題的表達式:
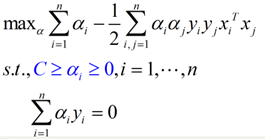
??? 藍色的部分是與線性可分的對偶問題表達式的不同之處。在線性不可分情況下得到的對偶問題,不同的地方就是α的范圍從[0, +∞),變為了[0, C],增加的懲罰ε沒有為對偶問題增加什么復雜度。
?
四、核函數:
??? 剛剛在談不可分的情況下,提了一句,如果使用某些非線性的方法,可以得到將兩個分類完美劃分的曲線,比如接下來將要說的核函數。
????我們可以讓空間從原本的線性空間變成一個更高維的空間,在這個高維的線性空間下,再用一個超平面進行劃分。這兒舉個例子,來理解一下如何利用空間的維度變得更高來幫助我們分類的(例子以及圖片來自pluskid的kernel函數部分):
??? 下圖是一個典型的線性不可分的情況

??? 但是當我們把這兩個類似于橢圓形的點映射到一個高維空間后,映射函數為:
![]() ??? 用這個函數可以將上圖的平面中的點映射到一個三維空間(z1,z2,z3),并且對映射后的坐標加以旋轉之后就可以得到一個線性可分的點集了。
??? 用這個函數可以將上圖的平面中的點映射到一個三維空間(z1,z2,z3),并且對映射后的坐標加以旋轉之后就可以得到一個線性可分的點集了。

?
?
?
?
??? 用另外一個哲學例子來說:世界上本來沒有兩個完全一樣的物體,對于所有的兩個物體,我們可以通過增加維度來讓他們最終有所區別,比如說兩本書,從(顏色,內容)兩個維度來說,可能是一樣的,我們可以加上?作者?這個維度,是在不行我們還可以加入?頁碼,可以加入?擁有者,可以加入?購買地點,可以加入?筆記內容等等。當維度增加到無限維的時候,一定可以讓任意的兩個物體可分了。
??? 回憶剛剛得到的對偶問題表達式:
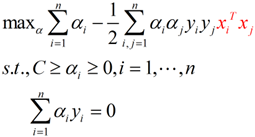
??? 我們可以將紅色這個部分進行改造,令:
![]() ???? 這個式子所做的事情就是將線性的空間映射到高維的空間,k(x, xj)有很多種,下面是比較典型的兩種:
???? 這個式子所做的事情就是將線性的空間映射到高維的空間,k(x, xj)有很多種,下面是比較典型的兩種:
 ??? 上面這個核稱為多項式核,下面這個核稱為高斯核,高斯核甚至是將原始空間映射為無窮維空間,另外核函數有一些比較好的性質,比如說不會比線性條件下增加多少額外的計算量,等等,這里也不再深入。一般對于一個問題,不同的核函數可能會帶來不同的結果,一般是需要嘗試來得到的。
??? 上面這個核稱為多項式核,下面這個核稱為高斯核,高斯核甚至是將原始空間映射為無窮維空間,另外核函數有一些比較好的性質,比如說不會比線性條件下增加多少額外的計算量,等等,這里也不再深入。一般對于一個問題,不同的核函數可能會帶來不同的結果,一般是需要嘗試來得到的。
?
五、一些其他的問題:
???? 1)如何進行多分類問題:
???? 上面所談到的分類都是2分類的情況,當N分類的情況下,主要有兩種方式,一種是1 vs (N – 1)一種是1 vs 1,前一種方法我們需要訓練N個分類器,第i個分類器是看看是屬于分類i還是屬于分類i的補集(出去i的N-1個分類)。
???? 后一種方式我們需要訓練N * (N – 1) / 2個分類器,分類器(i,j)能夠判斷某個點是屬于i還是屬于j。
???? 這種處理方式不僅在SVM中會用到,在很多其他的分類中也是被廣泛用到,從林教授(libsvm的作者)的結論來看,1 vs 1的方式要優于1 vs (N – 1)。
???? 2)SVM會overfitting嗎?
???? SVM避免overfitting,一種是調整之前說的懲罰函數中的C,另一種其實從式子上來看,min ||w||^2這個看起來是不是很眼熟?在最小二乘法回歸的時候,我們看到過這個式子,這個式子可以讓函數更平滑,所以SVM是一種不太容易over-fitting的方法。
?
參考文檔:
??? 主要的參考文檔來自4個地方,wikipedia(在文章中已經給出了超鏈接了),pluskid關于SVM的博文,Andrew moore的ppt(文章中不少圖片都是引用或者改自Andrew Moore的ppt,以及prml

 和KKT條件)

)















