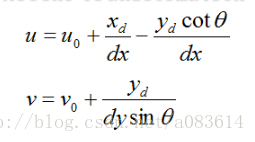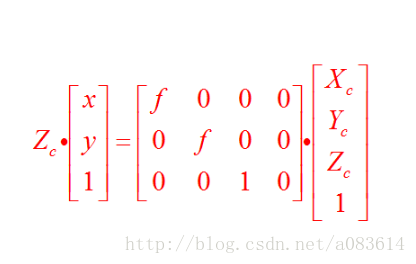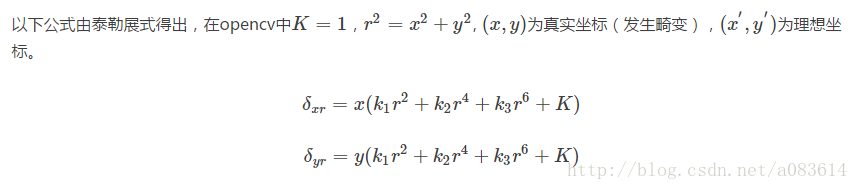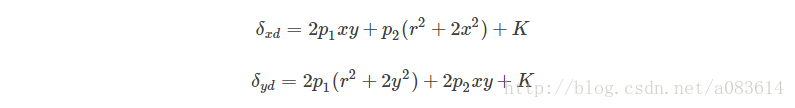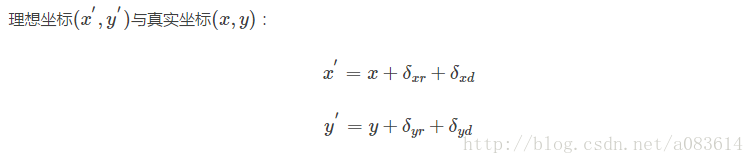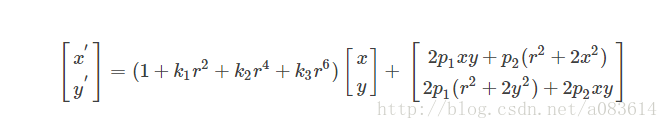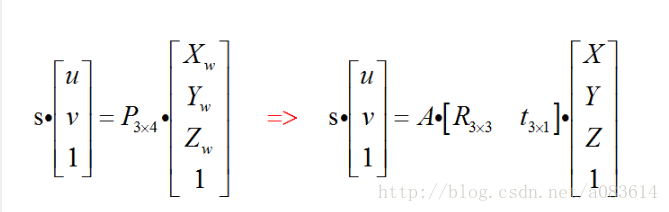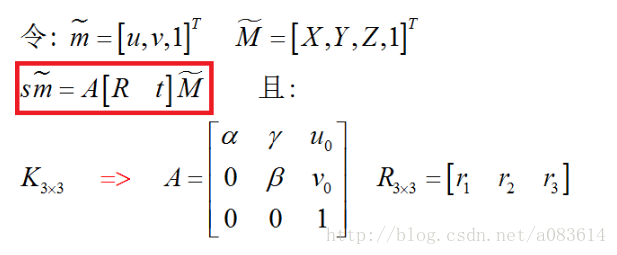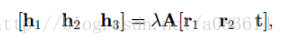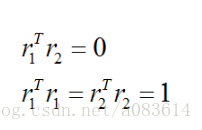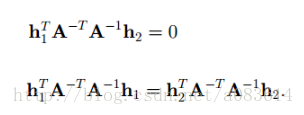相機標定詳解
最近做項目要用到標定,因為是小白,很多東西都不懂,于是查了一堆的博客,但沒有一個博客能讓我完全能看明白整個過程,絕大多數都講的不全面,因此自己總結了一篇博客,給自己理一下思路,也能夠幫助大家。(張正友標定的詳細求解還未完全搞明白,后面再加)
參考博客:?
相機標定(Camera calibration)原理、步驟?
(http://blog.csdn.net/lql0716/article/details/71973318?locationNum=8&fps=1)
相機標定內容詳解?(轉載自祥的博客)?
(http://blog.csdn.net/humanking7/article/details/44756073)
張正友標定介紹?
(http://blog.csdn.net/heroacool/article/details/50286677)
[圖像]攝像機標定(2) 張正友標定推導詳解?
(http://blog.csdn.net/humanking7/article/details/44756235)
MATLAB–相機標定教程?
(http://blog.csdn.net/heroacool/article/details/51023921)
在圖像測量過程以及機器視覺應用中,為確定空間物體表面某點的三維幾何位置與其在圖像中對應點之間的相互關系,必須建立相機成像的幾何模型,這些幾何模型參數就是相機參數。在大多數條件下這些參數必須通過實驗與計算才能得到,這個求解參數(內參、外參、畸變參數)的過程就稱之為相機標定(或攝像機標定)。無論是在圖像測量或者機器視覺應用中,相機參數的標定都是非常關鍵的環節,其標定結果的精度及算法的穩定性直接影響相機工作產生結果的準確性。因此,做好相機標定是做好后續工作的前提,提高標定精度是科研工作的重點所在。?
畸變(distortion)是對直線投影(rectilinear projection)的一種偏移。簡單來說直線投影是場景內的一條直線投影到圖片上也保持為一條直線。畸變簡單來說就是一條直線投影到圖片上不能保持為一條直線了,這是一種光學畸變(optical aberration),可能由于攝像機鏡頭的原因。
坐標轉換基礎
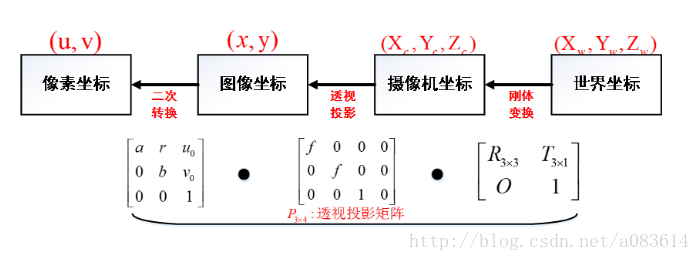
在視覺測量中,需要進行的一個重要預備工作是定義四個坐標系的意義,即?攝像機坐標系?、?圖像物理坐標系、 像素坐標系?和?世界坐標系(參考坐標系)?。
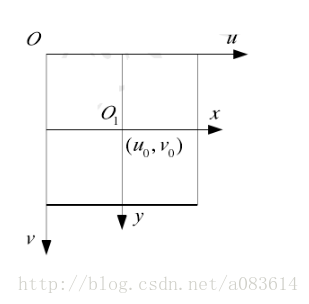
一、圖像坐標系(x,y)至像素坐標系(u,v)
1.兩坐標軸互相垂直
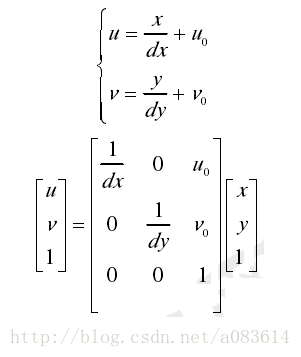
此時有
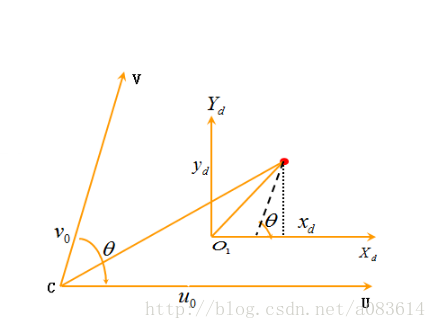
2.一般情況,兩軸不互相垂直(圖像畸變)
此時有
寫成矩陣形式為:
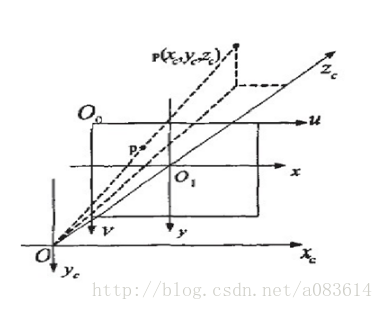
二、相機坐標系(Xc,Yc,Zc)至圖像坐標系(x,y)
(根據小孔成像原理,圖像坐標系應在相機坐標系的另一邊,為倒立反向成像,但為方便理解和計算,故投影至同側。)
根據三角形相似性原理得:
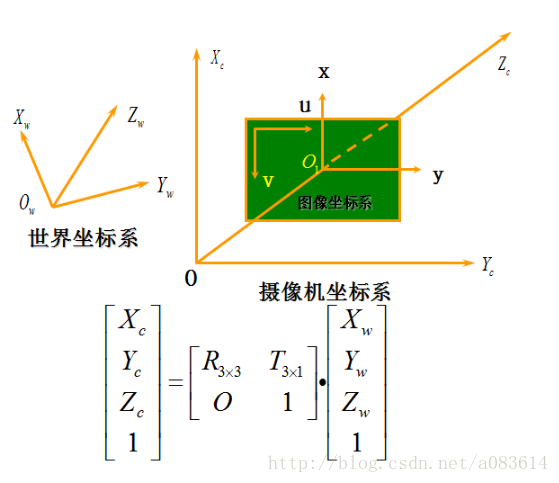
三、世界坐標系(Xw,Yw,Zw)至相機坐標系(Xc,Yc,Zc)
四、合并公式
R、T矩陣為相機的外參矩陣。
畸變
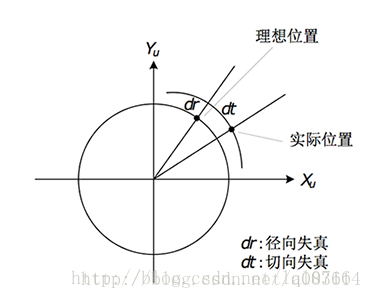
畸變一般可以分為:徑向畸變、切向畸變
徑向畸變來自于透鏡形狀。?
切向畸變來自于整個攝像機的組裝過程。
畸變還有其他類型的畸變,但是沒有徑向畸變、切向畸變顯著,所以忽略不計。
徑向畸變(桶形畸變和枕形畸變):
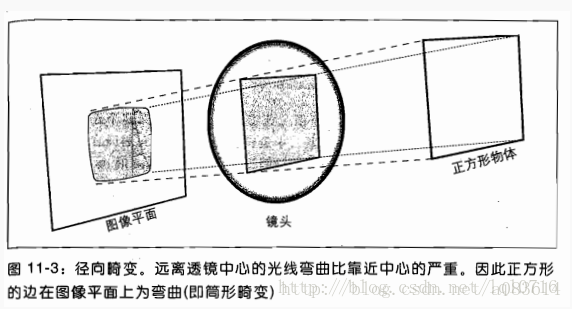
實際攝像機的透鏡總是在成像儀的邊緣產生顯著的畸變,這種現象來源于“筒形”或“魚眼”的影響。?
如下圖,光線在原理透鏡中心的地方比靠近中心的地方更加彎曲。對于常用的普通透鏡來說,這種現象更加嚴重。筒形畸變在便宜的網絡攝像機中非常厲害,但在高端攝像機中不明顯,因為這些透鏡系統做了很多消除徑向畸變的工作。?對于徑向畸變,成像儀中心(光學中心)的畸變為0,隨著向邊緣移動,畸變越來越嚴重。?
對于徑向畸變可以通過下面的泰勒級數展開式進行校正:??
這里的x、y是圖像中的畸變后的位置坐標,通過校正得到真實坐標。r是該點距成像中心的距離。
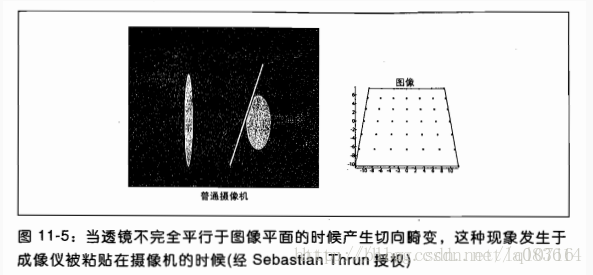
切向畸變(薄透鏡畸變和離心畸變):
切向畸變是由于透鏡制造上的缺陷使得透鏡本身與圖像平面不平行而產生的。
切向畸變可以通過如下公式來矯正:?
?
這里的x、y是圖像中的畸變后的位置坐標,通過校正得到真實坐標。r是該點距成像中心的距離。
opencv畸變模型
徑向畸變模型:
切向畸變模型:
可得:
由公式可得畸變有k1,k2,k3,p1,p2五個參數,對于質量比較好的相機來說,切向畸變很小,可忽略,徑向畸變系數k3也可忽略,只計算k1,k2兩個參數。張正友標定中就默認為p1,p2為0。
張正學標定中的畸變模型:
標定方法
1、傳統相機標定
最簡單的相機標定為線性標定,即不考慮相機的畸變而只考慮空間坐標轉換。?
每個坐標點有X,Y兩個變量,可列兩個方程,相機內參有5個未知數,外參平移和旋轉各3個,共有11個變量,因此至少需要6個特征點來求解。
2、非線性標定
當鏡頭畸變明顯時必須考慮畸變,一般較為便宜的網絡攝像頭畸變特別大,而價格較貴的工業攝像頭則畸變很小,因為其中已經嵌入了許多消除畸變的程序。這時線性模型轉化為非線性模型,需要通過非線性標定方法求解。有最速下降法,遺傳算法,高斯牛頓法和神經網絡算法等。
3、張正友標定介紹
(張正友標定只考慮了徑向畸變,沒有考慮切向畸變)
由上面的坐標轉換可得:
我們把世界坐標系放置在標定板平面上,令Z=0,這時有:
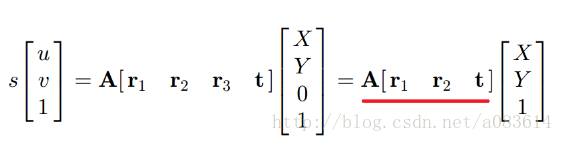
H為3X3矩陣,并且有一個元素作為齊次坐標,則有8個未知元素,一組坐標對應兩個方程,則至少需要四組對應的點即可算出單應性矩陣H。
有
旋轉矩陣為正交矩陣,因此有以下性質:
代入可得
由此可求出單應性矩陣A,因A有5個元素,則至少需要三個單應性矩陣方能求解,那么就需要三張不同的標定圖片,這就是為什么標定需要用至少3張以上的圖片的原因之一(我還不是完全確定是這樣)
3.2.3 標定
相機標定步驟:
1、打印一張棋盤格,把它貼在一個平面上,作為標定物。?
2、通過調整標定物或攝像機的方向,為標定物拍攝一些不同方向的照片。?
3、從照片中提取棋盤格角點。?
4、估算理想無畸變的情況下,五個內參和六個外參。?
5、應用最小二乘法估算實際存在徑向畸變下的畸變系數。?
6、極大似然法,優化估計,提升估計精度。
Matlab工具箱標定:
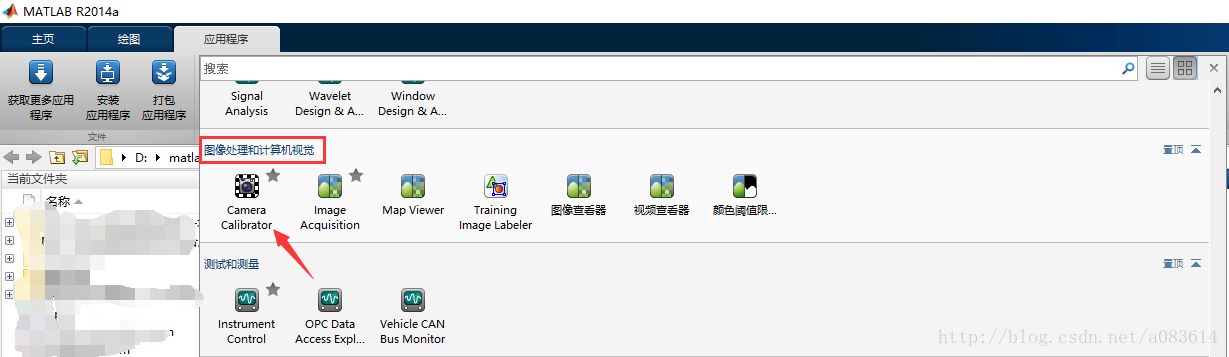
1、應用程序中找到Camera Calibration
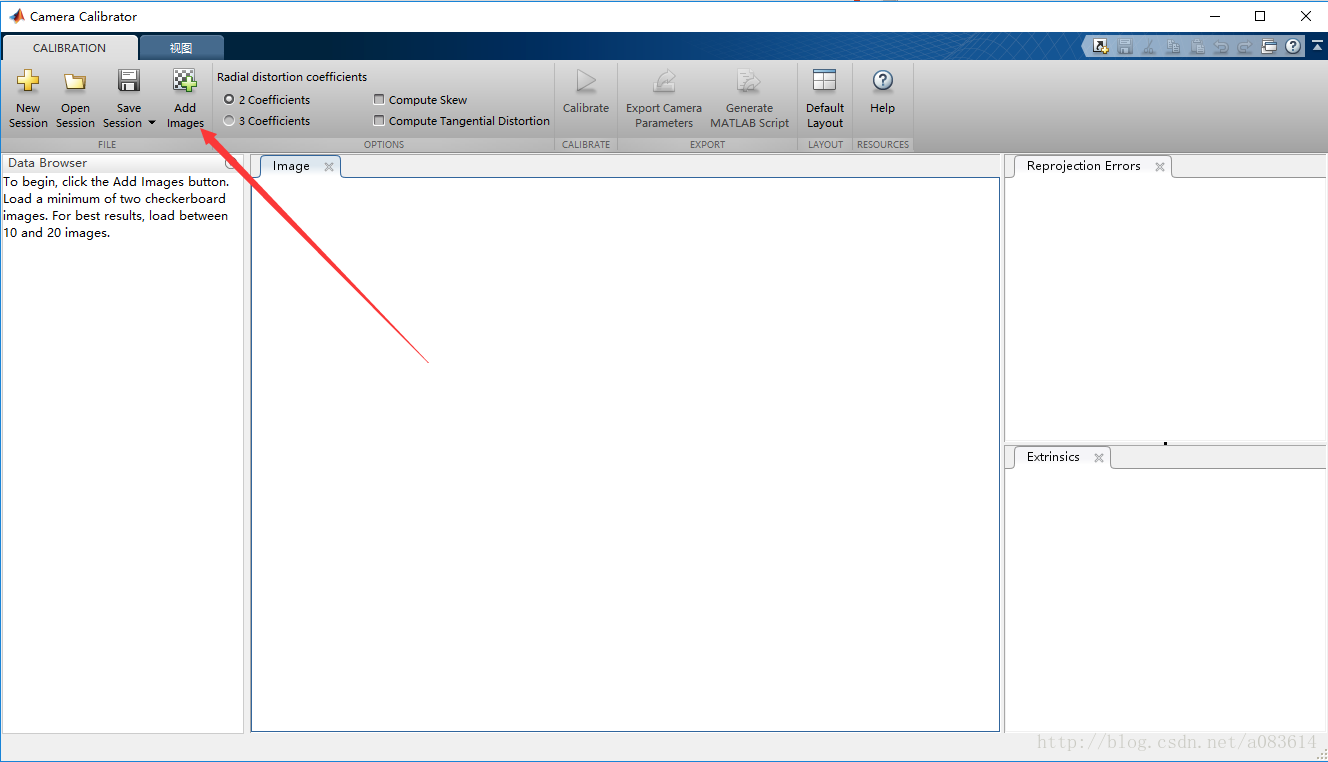
2、添加標定板拍攝圖片(按Ctrl可一次添加多張)
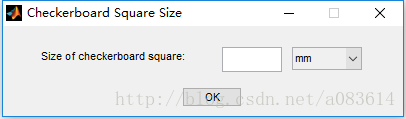
3、輸入棋盤格每格的尺寸大小
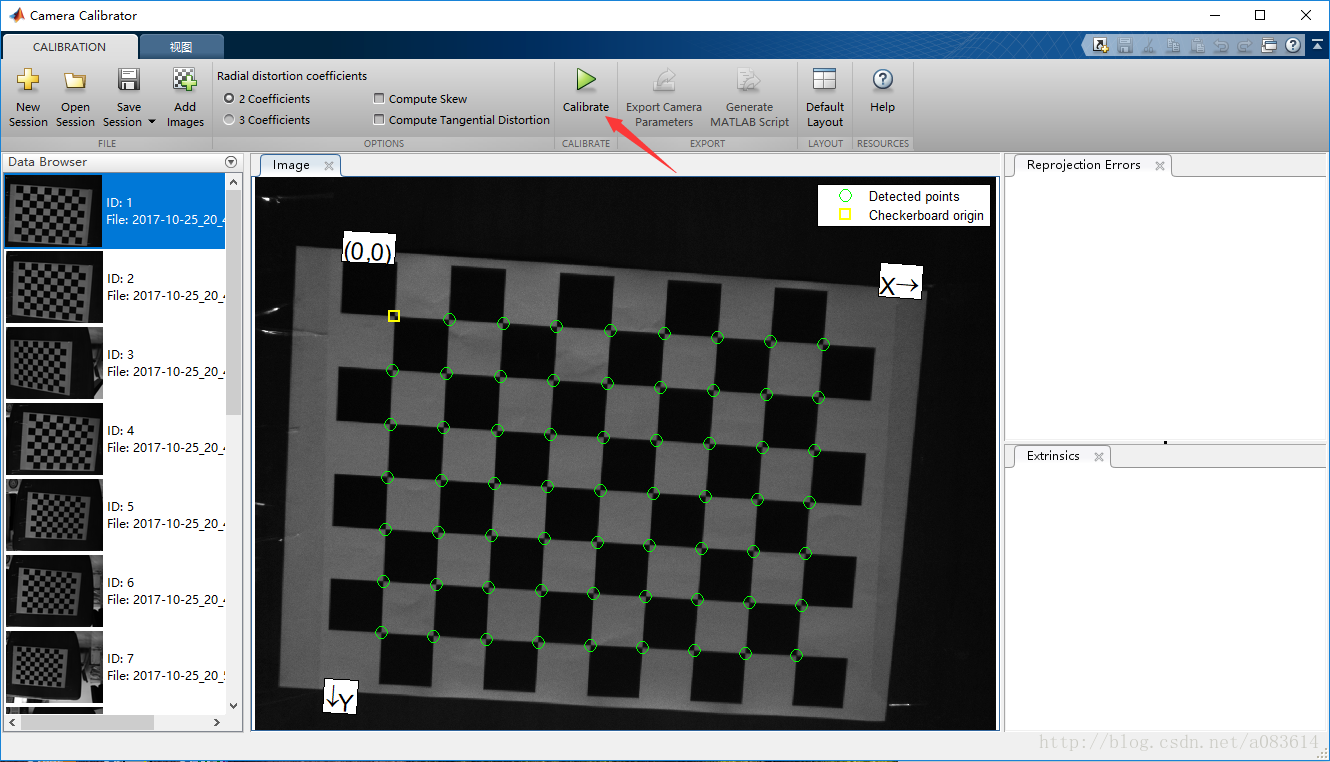
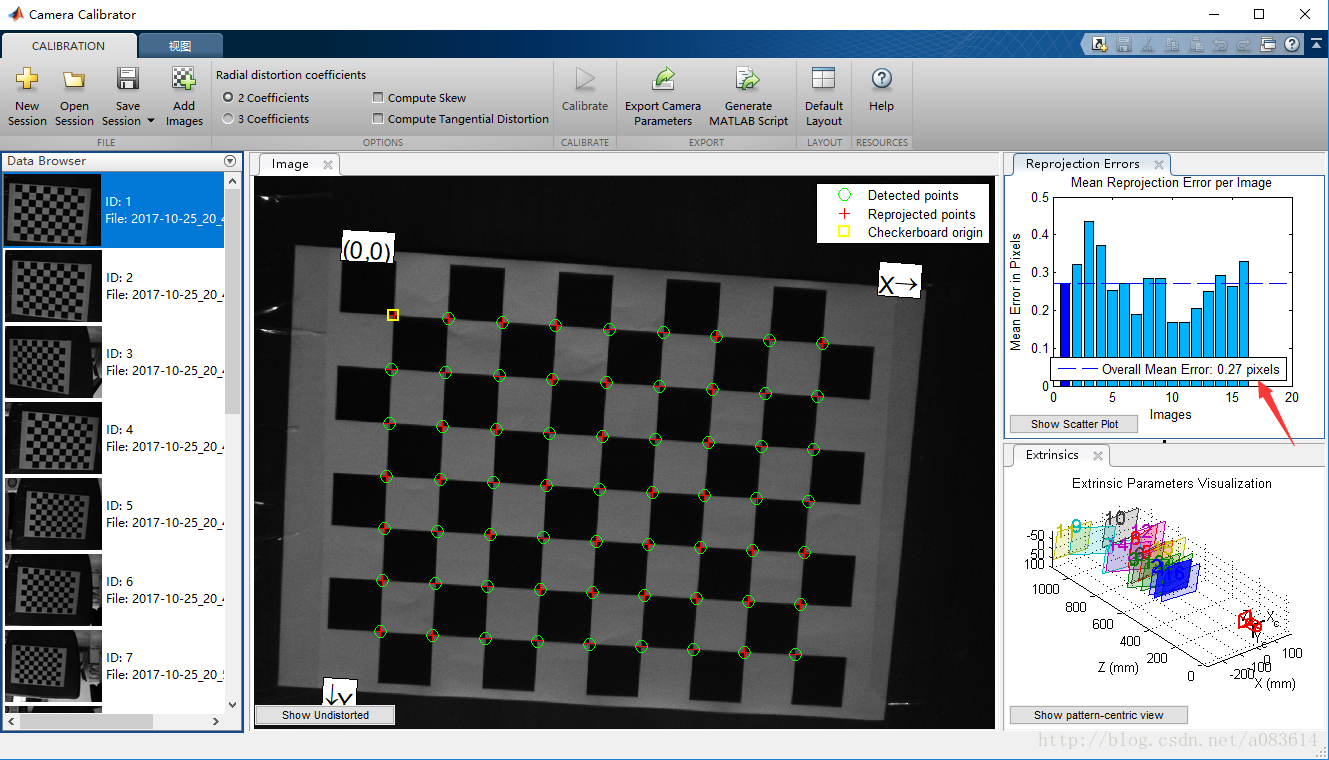
4、顯示已檢測出的棋盤格,點擊Calibration,開始標定。
5、得到標定結果(平均誤差小于0.5即可認為結果可靠,這個地方我還不是很清楚)
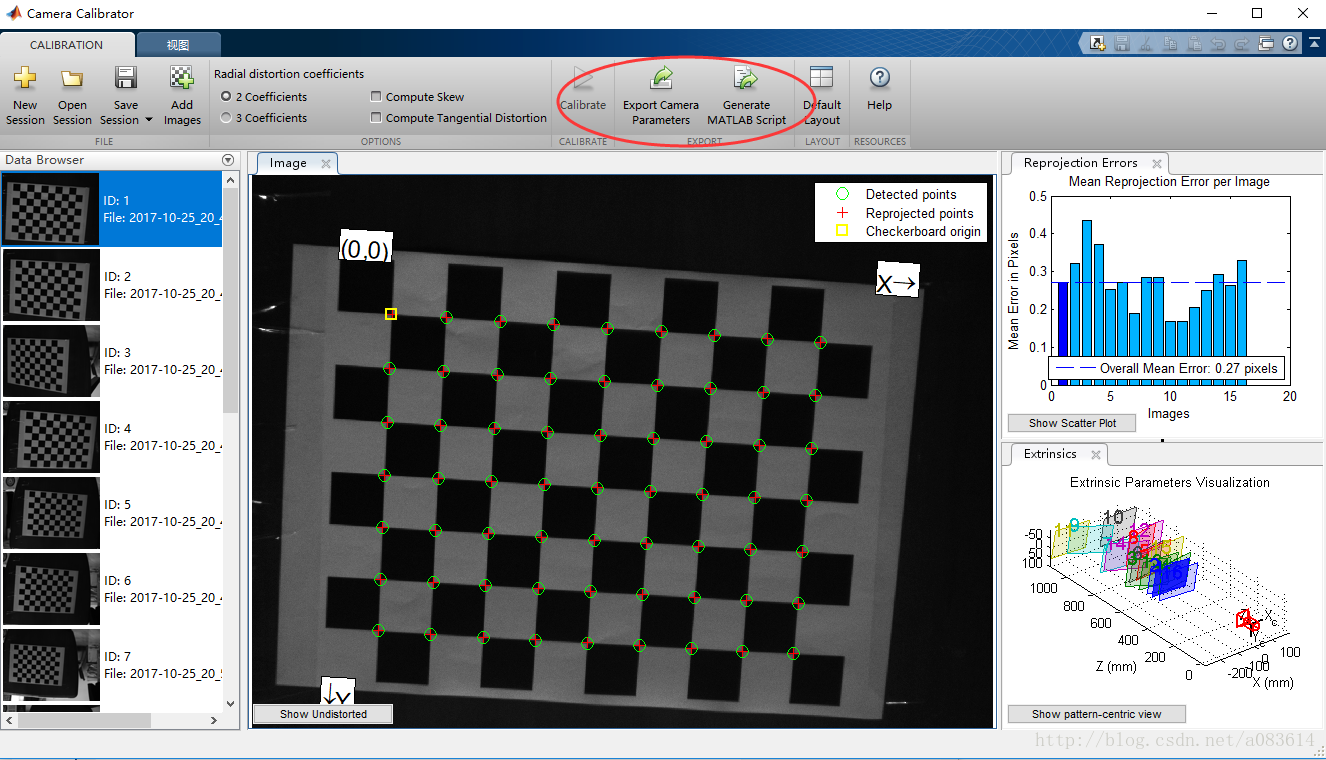
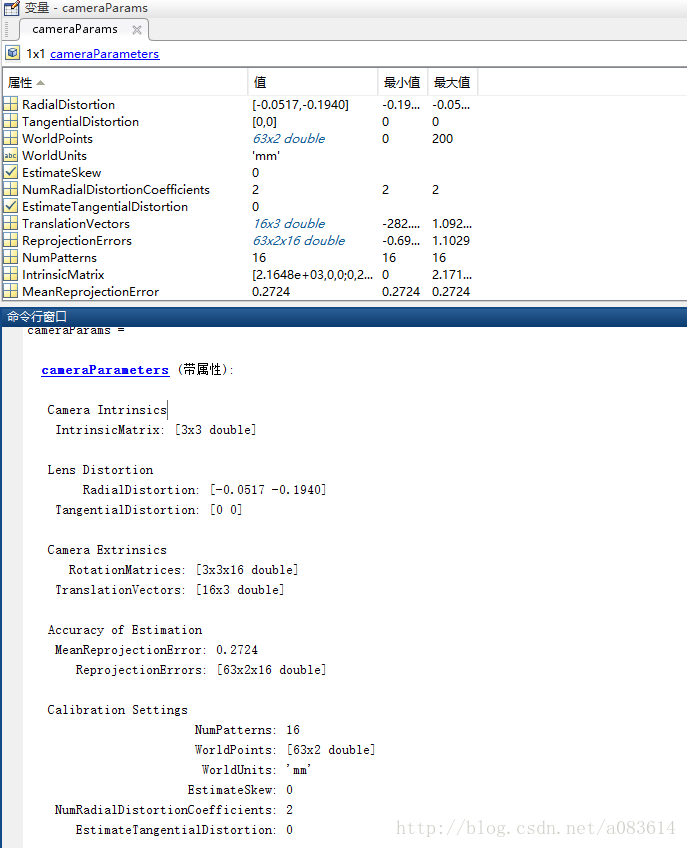
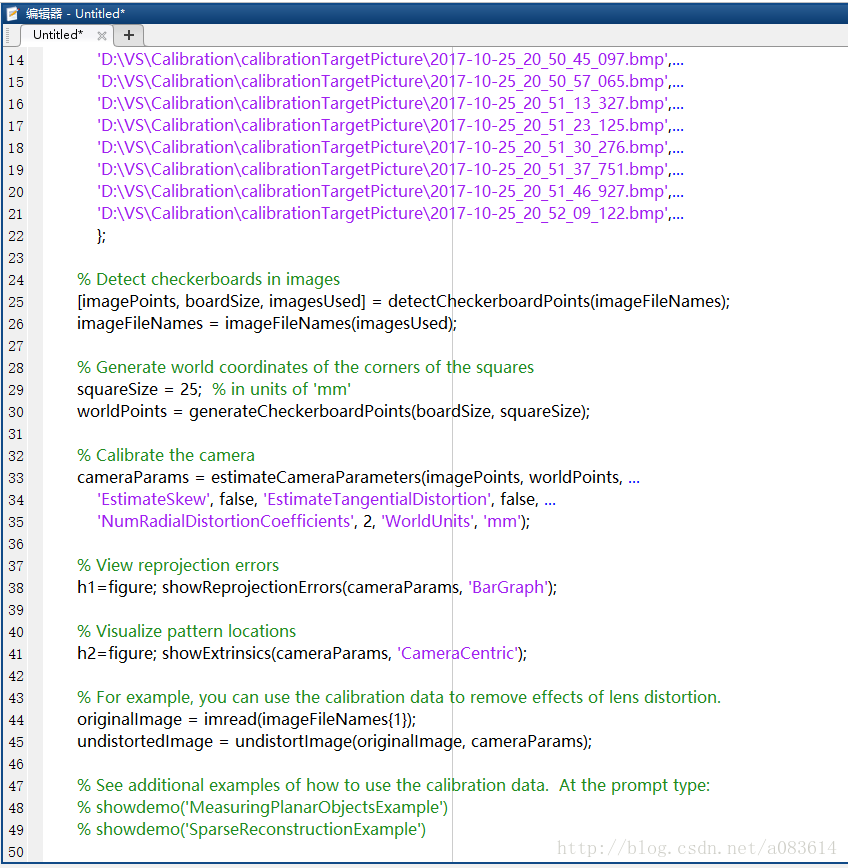
6、可查看標定結果和程序