前言

實際工作中經常會用到一些聚類算法對一些數據進行聚類處理，如何評估每次聚類效果的好壞？可選的方法有1、根據一些聚類效果的指標來評估；2、直接打點。今天就主要總結下這段時間了解的聚類效果評估指標。廢話少說，直接上干貨。

針對數據有類別標簽的情況

Adjusted Rand index (ARI)

優點：
1.1 對任意數量的聚類中心和樣本數，隨機聚類的ARI都非常接近于0；
1.2 取值在［－1，1］之間，負數代表結果不好，越接近于1越好；
1.3 可用于聚類算法之間的比較
缺點：
1.4 ARI需要真實標簽

Mutual Information based scores (MI) 互信息

優點：除取值范圍在［0，1］之間，其他同ARI；可用于聚類模型選擇
缺點：需要先驗知識

針對數據無類別標簽的情況

對于無類標的情況，沒有唯一的評價指標。對于數據凸分布的情況我們只能通過類內聚合度、類間低耦合的原則來作為指導思想。

輪廓系數（Silhouette Coefficient）

定義
輪廓系數（Silhouette Coefficient），是聚類效果好壞的一種評價方式。最早由 Peter J. Rousseeuw 在 1986 提出。它結合內聚度和分離度兩種因素。可以用來在相同原始數據的基礎上用來評價不同算法、或者算法不同運行方式對聚類結果所產生的影響。

原理

（1）計算樣本i到同簇其他樣本的平均距離ai。ai 越小，說明樣本i越應該被聚類到該簇。將ai 稱為樣本i的簇內不相似度。某一個簇C中所有樣本的a i 均值稱為簇C的簇不相似度。

（2）計算樣本i到其他某簇Cj 的所有樣本的平均距離bij，稱為樣本i與簇Cj 的不相似度。定義為樣本i的簇間不相似度：bi =min{bi1, bi2, …, bik}，即某一個樣本的簇間不相似度為該樣本到所有其他簇的所有樣本的平均距離中最小的那一個。
bi越大，說明樣本i越不屬于其他簇。

（3）根據樣本i的簇內不相似度a i 和簇間不相似度b i ，定義某一個樣本樣本i的輪廓系數：
樣例圖：

如上圖所示，最終整個數據的輪廓系數=每個樣本輪廓系數之和/n(即所有樣本輪廓系數的平均值)

（4）判斷：
si接近1，則說明樣本i聚類合理；
si接近-1，則說明樣本i更應該分類到另外的簇；
若si 近似為0，則說明樣本i在兩個簇的邊界上。

（5） 所有樣本的輪廓系數S

所有樣本的s i 的均值稱為聚類結果的輪廓系數，定義為S，是該聚類是否合理、有效的度量。聚類結果的輪廓系數的取值在【-1,1】之間，值越大，說明同類樣本相距約近，不同樣本相距越遠，則聚類效果越好。

優缺點總結
優點：
對于不正確的 clustering （聚類），分數為 -1 ， highly dense clustering （高密度聚類）為 +1 。零點附近的分數表示 overlapping clusters （重疊的聚類）。
當 clusters （簇）密集且分離較好時，分數更高，這與 cluster （簇）的標準概念有關。
缺點：
convex clusters（凸的簇）的 Silhouette Coefficient 通常比其他類型的 cluster （簇）更高，例如通過 DBSCAN 獲得的基于密度的 cluster（簇）。不適用與基于密度的算法。

使用：
sklearn中的接口

輪廓系數以及其他的評價函數都定義在sklearn.metrics模塊中，

在sklearn中函數silhouette_score()計算所有點的平均輪廓系數，而silhouette_samples()返回每個點的輪廓系數。后面會給出具體的例子的。它的定義如下：

def silhouette_score(X, labels, metric='euclidean', sample_size=None,
random_state=None, **kwds):
'''
X：表示要聚類的樣本數據，一般形如（samples，features）的格式
labels：即聚類之后得到的label標簽，形如（samples，）的格式
metric：默認是歐氏距離
'''

CH分數（Calinski Harabasz Score ）

原理：
也稱之為 Calinski-Harabaz Index
分數S被定義為簇間離散與簇內離散的比率，是通過評估類之間方差和類內方差來計算得分。該分值越大說明聚類效果越好

其中k代表聚類類別數，N代表全部數據數目。
n是樣本點數，cq是在聚類q中的樣本點，Cq是在聚類q中的中心點，nq是聚類q中的樣本點數量，c是E的中心（E是所有的數據集）

trace只考慮了矩陣對角上的元素，即類q中所有數據點到類q中心點的歐幾里得距離。

類別內部數據的協方差越小越好，類別之間的協方差越大越好，這樣的Calinski-Harabasz分數會高。 總結起來一句話：CH index的數值越大越好。

在真實的分群label不知道的情況下，可以作為評估模型的一個指標。 同時，數值越小可以理解為：組間協方差很小，組與組之間界限不明顯。
與輪廓系數的對比，最大的優勢：快！相差幾百倍！毫秒級（原因：可能是計算簇間，簇內不相似度對應的數據量和計算復雜度不同。CH有中心點，只需要計算簇內點到中心點的距離即可，簇間有整個樣本的中點，只需要計算各簇中心點到整個樣本的中心點即可；而輪廓系數則需要在簇內計算樣本i到同簇其他所有樣本的平均距離等。一個是固定中心點計算，一個是沒有中心點，計算所有的樣本點距離。）

優缺點總結
優點
當 cluster （簇）密集且分離較好時，分數更高，這與一個標準的 cluster（簇）有關。
得分計算很快。

缺點
凸的簇的 Calinski-Harabaz index（Calinski-Harabaz 指數）通常高于其他類型的 cluster（簇），例如通過 DBSCAN 獲得的基于密度的 cluster（簇）。

使用
在sklearn中的接口

在scikit-learn中， Calinski-Harabasz Index對應的方法是metrics.calinski_harabaz_score. 它的定義如下：

def calinski_harabasz_score(X, labels):
'''
X：表示要聚類的樣本數據，一般形如（samples，features）的格式
labels：即聚類之后得到的label標簽，形如（samples，）的格式

戴維森堡丁指數(DBI)——davies_bouldin_score

定義
戴維森堡丁指數(DBI)，又稱為分類適確性指標，是由大衛L·戴維斯和唐納德·Bouldin提出的一種評估聚類算法優劣的指標

原理
DB計算任意兩類別的類內距離平均距離(CP)之和除以兩聚類中心距離求最大值。DB越小意味著類內距離越小同時類間距離越大
缺點：因使用歐式距離 所以對于環狀分布 聚類評測很差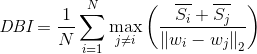
分子：簇內所有點到該簇質心點的平均距離之和
分母d(ci,cj)：兩類別質心間的距離
max()最大值部分：選取每組比例中的最大值（即選取最糟糕的一組）
1/n求和部分：將所選比例加和除以類別數
結果意義：DB值越小表示聚類結果同簇內部緊密，不同簇分離較遠。即類內距離越小，類間距離越大。

實例

具體過程：
step1：計算每個聚類d(A)，d(B)，d?的平均內部距離。
step2：計算任意質心間的距離d(A,B)，d(A,C)和d(B,C)。
step3：返回最大比例（任意內部聚類之和與其質心間距之比）

注意：DBI的值最小是0，值越小，代表聚類效果越好。

使用
DBI的sklearn中的定義：

def davies_bouldin_score(X, labels):
'''
X：表示要聚類的樣本數據，一般形如（samples，features）的格式
labels：即聚類之后得到的label標簽，形如（samples，）的格式

Compactness(緊密性)(CP)

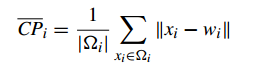
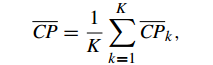
CP計算每一個類各點到聚類中心的平均距離CP越低意味著類內聚類距離越近。著名的 K-Means 聚類算法就是基于此思想提出的。
缺點：沒有考慮類間效果

Separation(間隔性)(SP)

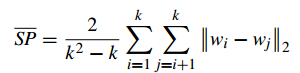
SP計算 各聚類中心兩兩之間平均距離，SP越高意味類間聚類距離越遠
缺點：沒有考慮類內效果

Dunn Validity Index (鄧恩指數)(DVI)

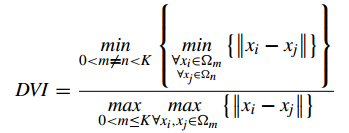
DVI計算任意兩個簇元素的最短距離(類間)除以任意簇中的最大距離(類內)。 DVI越大意味著類間距離越大同時類內距離越小
缺點：對離散點的聚類測評很高、對環狀分布測評效果差

其他

其他的一些指標如：均一性（一個簇中只包含一個類別）和完整性（同類別被分到同簇中）就類似于之前半監督中的準確率和召回率。
V-measure：均一性和完整性的加權平均

兩個指標用來衡量分類效果：即ARI就相當于之前的F1，Fβ

總結

常用的聚類指標可能就是輪廓系數，CH分數，DBI等。針對不同的數據量，這些指標的計算效率會有差距。若數據量小都可以嘗試使用，但要注意各個指標的使用場景。若數據量大則建議使用CH分數，實測該指標的計算效率的確很高，至于原因就如前文所描述的那樣。