前言

KNN一般用于有監督的分類場景，除此之外，KNN在異常檢測場景中也有應用，下面主要介紹下KNN在這兩面的應用原理。

KNN做分類的原理

計算步驟如下：
1）算距離：給定測試對象，計算它與訓練集中的每個對象的距離
2）找鄰居：圈定距離最近的k個訓練對象，作為測試對象的近鄰
3）做分類：根據這k個近鄰歸屬的主要類別，來對測試對象分類
（看未知類別樣本最近的K個樣本的類別，那種類別多，樣本就屬于那種類別！）

優缺點

KNN優點：

理論成熟，思想簡單，既可以用來做分類也可以用來做回歸
可用于非線性分類
訓練時間復雜度比支持向量機之類的算法低，僅為O(n)
和樸素貝葉斯之類的算法比，對數據沒有假設，準確度高，對異常點不敏感
由于KNN方法主要靠周圍有限的鄰近的樣本，而不是靠判別類域的方法來確定所屬類別的，因此對于類域的交叉或重疊較多的待分樣本集來說，KNN方法較其他方法更為適合
該算法比較適用于樣本容量比較大的類域的自動分類，而那些樣本容量較小的類域采用這種算法比較容易產生誤分

KNN 缺點

計算量大，尤其是特征數非常多的時候
樣本不平衡的時候，對稀有類別的預測準確率低
KD樹，球樹之類的模型建立需要大量的內存
使用懶散學習方法，基本上不學習，導致預測時速度比起邏輯回歸之類的算法慢
相比決策樹模型，KNN模型可解釋性不強（雞蛋里挑骨頭了）

適用場景

它的適用面很廣，并且在樣本量足夠大的情況下準確度很高。不適用于特征維度比較多的場景（幾十維即可）。

參數詳解

class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None, **kwargs)

常用參數：algorithm、n_neighbors、weights、p 等超參數
第一個超參數：algorithm（一般設為auto即可）
algorithm 即建立 kNN 模型時采用什么算法去搜索最近的 k 個點，有四個選項：

brute（暴力搜索）
kd_tree（KD樹）
ball_tree（球樹）
auto（默認值，自動選擇上面三種速度最快的）

之前建立模型時沒有設置這個參數，模型默認使用了 auto 方法，不過還是有必要了解一下這幾種方法的區別。
首先，我們知道 KNN 模型的核心思想是計算大量樣本點之間的距離。
第一種算法 brute （暴力搜索）。意思就是計算預測樣本和全部訓練集樣本的距離，最后篩選出前 K 個最近的樣本，這種方法很蠻力，所以叫暴力搜索。當樣本和特征數量很大的時候，每計算一個樣本距離就要遍歷一遍訓練集樣本，很費時間效率低下。有什么方法能夠做到無需遍歷全部訓練集就可以快速找到需要的 k 個近鄰點呢？這就要用到 KD 樹和球樹算法。

第二種算法 KD 樹（K-dimension tree縮寫）。簡單來說 KD 樹是一種「二叉樹」結構，就是把整個空間劃分為特定的幾個子空間，然后在合適的子空間中去搜索待預測的樣本點。采用這種方法不用遍歷全部樣本就可以快速找到最近的 K 個點，速度比暴力搜索快很多（稍后會用實例對比一下）。至于什么是二叉樹，這就涉及到數據結構的知識，稍微有些復雜，就目前來說暫時不用深入了解，sklearn 中可以直接調用 KD 樹，很方便。
假設數據集樣本數為 m，特征數為 n，則當樣本數量 m 大于 2 的 n 次方時，用 KD 樹算法搜索效果會比較好。比如適合 1000 個樣本且特征數不超過 10 個（2 的 10 次方為 1024）的數據集。一旦特征過多，KD 樹的搜索效率就會大幅下降，最終變得和暴力搜索差不多。通常來說 KD 樹適用維數不超過 20 維的數據集，超過這個維數可以用球樹這種算法。

第三種算法是球樹（Ball tree）。對于一些分布不均勻的數據集，KD 樹算法搜索效率并不好，為了優化就產生了球樹這種算法。同樣的，暫時先不用具體深入了解這種算法。
當數據集樣本數量 m > 2 的 n 次方時，kd_tree 和 ball_tree 速度比 brute 暴力搜索快了一個量級，auto 采用其中最快的算法。
我們介紹了第一個超參數 algorithm，就 kNN 算法來說通常只需要設置 auto 即可，讓模型自動為我們選擇合適的算法。

第二個超參數：n_neighbors
n_neighbors 即要選擇最近幾個點，默認值是 5（等效 k )。

k值過大和過小造成的影響：
k值較小，就相當于用較小的領域中的訓練實例進行預測，訓練誤差近似誤差小（偏差小），泛化誤差會增大（方差大），換句話說，K值較小就意味著整體模型變得復雜，容易發生過擬合；

k值較大，就相當于用較大領域中的訓練實例進行預測，泛化誤差小（方差小），但缺點是近似誤差大（偏差大），換句話說，K值較大就意味著整體模型變得簡單，容易發生欠擬合；一個極端是k等于樣本數m，則完全沒有分類，此時無論輸入實例是什么，都只是簡單的預測它屬于在訓練實例中最多的類，模型過于簡單。

對于k值的選擇，沒有一個固定的經驗（sklearn默認為5），一般根據樣本的分布，選擇一個較小的值，可以通過交叉驗證選擇一個合適的k值。

第三個超參數：距離權重 weights
剛才在劃分黃色點分類時，最近的 3 個點中紅綠色點比例是 2:1，所以我們就把黃色點劃分為紅色點了。
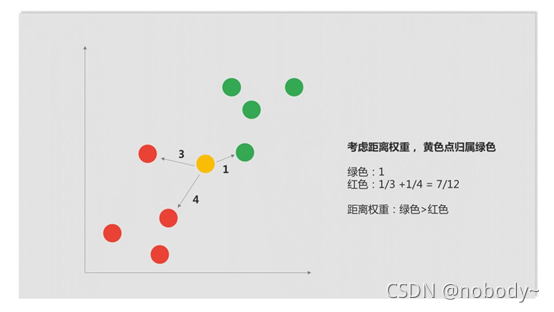
在這里插入圖片描述
這樣做忽略了點與點之間的距離問題：雖然紅點數量多于綠點，但顯然綠點距離黃點更近，把黃點劃分為綠色類可能更合適。因此，之前的模型效果可能并不好。
所以，在建立模型時，還可以從距離出發，將樣本權重與距離掛鉤，近的點權重大，遠的點權重小。怎么考慮權重呢，可以用取倒數這個簡單方法實現。
以上圖為例，綠點距離是 1，取倒數權重還為 1；兩個紅點的距離分別是 3 和 4，去倒數相加后紅點權重和為 7/12。綠點的權重大于紅點，所以黃點屬于綠色類。
在 Sklearn 的 kNN 模型中有專門考慮權重的超參數：weights，它有兩個選項：
Uniform：不考慮距離權重，默認值
Distance：考慮距離權重

第四個超參數：p
說到距離，還有一個重要的超參數 p。
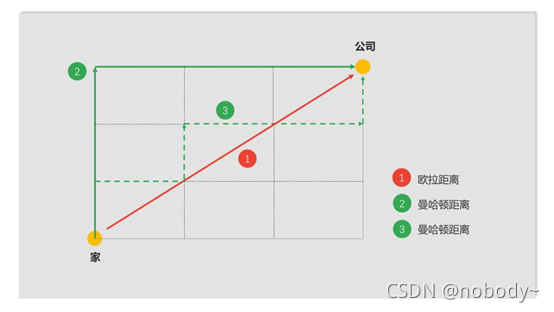
如果還記得的話，之前的模型在計算距離時，采用的是歐拉距離：
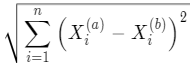
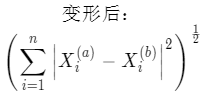
在這里插入圖片描述

除了歐拉距離，還有一種常用的距離，曼哈頓距離：

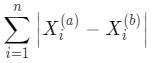
這兩種距離很好理解，舉個例子，從家到公司，歐拉距離就是二者的直線距離，但顯然不可能以直線到公司，而只能按著街道線路過去，這就是曼哈頓距離，俗稱出租車距離。
在這里插入圖片描述
這兩種格式很像，其實他們有一個更通用的公式：

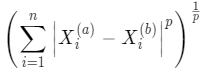
這就是明可夫斯基距離（Minkowski Distance），曼哈頓距離和歐拉距離分別是 p 為 1 和 2 的特殊值。
使用不同的距離計算公式，點的分類很可能不一樣導致模型效果也不一樣。

在 Sklearn 中對應這個距離的超參數是 p，默認值是 2，也就是歐拉距離。

KNN用作異常點檢測的原理

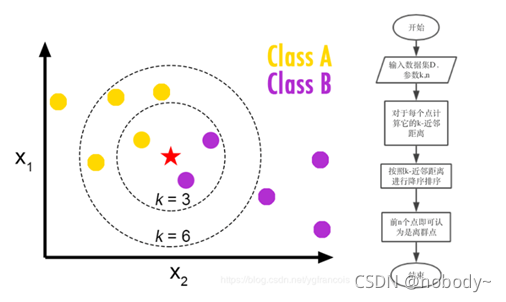
在這里插入圖片描述

比較簡單的做法是計算預測數據點與最近的K個樣本點的距離和，然后根據閾值進行異常樣本的判別(如若假設異常樣本量占總樣本量的1%，那么對數據集中每個數據點得到的距離和進行排序，挑選出Top1%即為異常值)。
K近鄰距離有多種設置：
1.距離第k近的點的距離
2.距離最近的k個點的平均距離
3.距離最近的k個點中的中間距離

PS：
這類方法有一種明顯的缺點，如果異常樣本數據較多，并且單獨成簇的話，最后得到的結果則不太樂觀。