一致性Hash算法

關于一致性Hash算法，在我之前的博文中已經有多次提到了，MemCache超詳細解讀一文中”一致性Hash算法”部分，對于為什么要使用一致性Hash算法、一致性Hash算法的算法原理做了詳細的解讀。

算法的具體原理這里再次貼上：

先構造一個長度為2^32的整數環(這個環被稱為一致性Hash環)，根據節點名稱的Hash值(其分布為[0, 2^32-1])將服務器節點放置在這個Hash環上，然后根據數據的Key值計算得到其Hash值(其分布也為[0, 2^32-1])，接著在Hash環上順時針查找距離這個Key值的Hash值最近的服務器節點，完成Key到服務器的映射查找。

這種算法解決了普通余數Hash算法伸縮性差的問題，可以保證在上線、下線服務器的情況下盡量有多的請求命中原來路由到的服務器。

當然，萬事不可能十全十美，一致性Hash算法比普通的余數Hash算法更具有伸縮性，但是同時其算法實現也更為復雜，本文就來研究一下，如何利用Java代碼實現一致性Hash算法。在開始之前，先對一致性Hash算法中的幾個核心問題進行一些探究。

數據結構的選取

一致性Hash算法最先要考慮的一個問題是：構造出一個長度為2^32的整數環，根據節點名稱的Hash值將服務器節點放置在這個Hash環上。

那么，整數環應該使用何種數據結構，才能使得運行時的時間復雜度最低？首先說明一點，關于時間復雜度，常見的時間復雜度與時間效率的關系有如下的經驗規則：

O(1) < O(log2N) < O(n) < O(N * logN) < O(N^2) < O(N^3) < 2^N < 3^N < N!

一般來說，前四個效率比較高，中間兩個差強人意，后三個比較差(只要N比較大，這個算法就動不了了)。OK，繼續前面的話題，應該如何選取數據結構，我認為有以下幾種可行的解決方案。

1、解決方案一：排序+List

我想到的第一種思路是：算出所有待加入數據結構的節點名稱的Hash值放入一個數組中，然后使用某種排序算法將其從小到大進行排序，最后將排序后的數據放入List中，采用List而不是數組是為了結點的擴展考慮。

之后，待路由的結點，只需要在List中找到第一個Hash值比它大的服務器節點就可以了，比如服務器節點的Hash值是[0,2,4,6,8,10]，帶路由的結點是7，只需要找到第一個比7大的整數，也就是8，就是我們最終需要路由過去的服務器節點。

如果暫時不考慮前面的排序，那么這種解決方案的時間復雜度：

(1)最好的情況是第一次就找到，時間復雜度為O(1)

(2)最壞的情況是最后一次才找到，時間復雜度為O(N)

平均下來時間復雜度為O(0.5N+0.5)，忽略首項系數和常數，時間復雜度為O(N)。

但是如果考慮到之前的排序，我在網上找了張圖，提供了各種排序算法的時間復雜度：

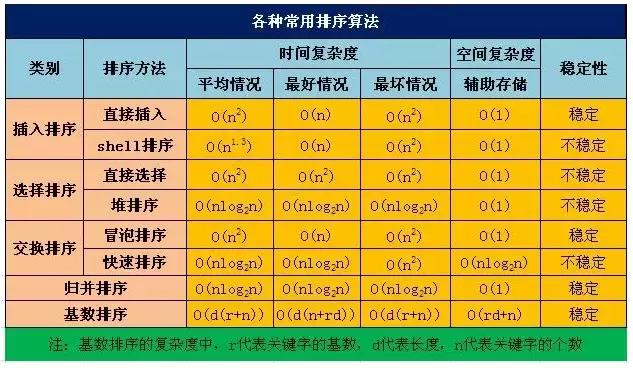
2、解決方案二：遍歷+List

既然排序操作比較耗性能，那么能不能不排序？可以的，所以進一步的，有了第二種解決方案。

解決方案使用List不變，不過可以采用遍歷的方式：

(1)服務器節點不排序，其Hash值全部直接放入一個List中

(2)帶路由的節點，算出其Hash值，由于指明了”順時針”，因此遍歷List，比待路由的節點Hash值大的算出差值并記錄，比待路由節點Hash值小的忽略

(3)算出所有的差值之后，最小的那個，就是最終需要路由過去的節點

在這個算法中，看一下時間復雜度：

1、最好情況是只有一個服務器節點的Hash值大于帶路由結點的Hash值，其時間復雜度是O(N)+O(1)=O(N+1)，忽略常數項，即O(N)

2、最壞情況是所有服務器節點的Hash值都大于帶路由結點的Hash值，其時間復雜度是O(N)+O(N)=O(2N)，忽略首項系數，即O(N)

所以，總的時間復雜度就是O(N)。其實算法還能更改進一些：給一個位置變量X，如果新的差值比原差值小，X替換為新的位置，否則X不變。這樣遍歷就減少了一輪，不過經過改進后的算法時間復雜度仍為O(N)。

總而言之，這個解決方案和解決方案一相比，總體來看，似乎更好了一些。

3、解決方案三：二叉查找樹

拋開List這種數據結構，另一種數據結構則是使用二叉查找樹。

當然我們不能簡單地使用二叉查找樹，因為可能出現不平衡的情況。平衡二叉查找樹有AVL樹、紅黑樹等，這里使用紅黑樹，選用紅黑樹的原因有兩點：

1、紅黑樹主要的作用是用于存儲有序的數據，這其實和第一種解決方案的思路又不謀而合了，但是它的效率非常高

2、JDK里面提供了紅黑樹的代碼實現TreeMap和TreeSet

另外，以TreeMap為例，TreeMap本身提供了一個tailMap(K fromKey)方法，支持從紅黑樹中查找比fromKey大的值的集合，但并不需要遍歷整個數據結構。

使用紅黑樹，可以使得查找的時間復雜度降低為O(logN)，比上面兩種解決方案，效率大大提升。

為了驗證這個說法，我做了一次測試，從大量數據中查找第一個大于其中間值的那個數據，比如10000數據就找第一個大于5000的數據(模擬平均的情況)。看一下O(N)時間復雜度和O(logN)時間復雜度運行效率的對比：

因為再大就內存溢出了，所以只測試到4000000數據。可以看到，數據查找的效率，TreeMap是完勝的，其實再增大數據測試也是一樣的，紅黑樹的數據結構決定了任何一個大于N的最小數據，它都只需要幾次至幾十次查找就可以查到。

當然，明確一點，有利必有弊，根據我另外一次測試得到的結論是，為了維護紅黑樹，數據插入效率TreeMap在三種數據結構里面是最差的，且插入要慢上5~10倍。

Hash值重新計算

服務器節點我們肯定用字符串來表示，比如”192.168.1.1″、”192.168.1.2″，根據字符串得到其Hash值，那么另外一個重要的問題就是Hash值要重新計算，這個問題是我在測試String的hashCode()方法的時候發現的，不妨來看一下為什么要重新計算Hash值：

/*** String的hashCode()方法運算結果查看* @author 嘵嘵**/public class StringHashCodeTest { public static void main(String[] args) { System.out.println("192.168.0.0:111的哈希值：" + "192.168.0.0:1111".hashCode()); System.out.println("192.168.0.1:111的哈希值：" + "192.168.0.1:1111".hashCode()); System.out.println("192.168.0.2:111的哈希值：" + "192.168.0.2:1111".hashCode()); System.out.println("192.168.0.3:111的哈希值：" + "192.168.0.3:1111".hashCode()); System.out.println("192.168.0.4:111的哈希值：" + "192.168.0.4:1111".hashCode()); }}

我們在做集群的時候，集群點的IP以這種連續的形式存在是很正常的。看一下運行結果為：

192.168.0.0:111的哈希值：1845870087192.168.0.1:111的哈希值：1874499238192.168.0.2:111的哈希值：1903128389192.168.0.3:111的哈希值：1931757540192.168.0.4:111的哈希值：1960386691

這個就問題大了，[0,2^32-1]的區間之中，5個HashCode值卻只分布在這么小小的一個區間，什么概念？[0,2^32-1]中有4294967296個數字，而我們的區間只有122516605，從概率學上講這將導致97%待路由的服務器都被路由到”192.168.0.1″這個集群點上，簡直是糟糕透了！

另外還有一個不好的地方：規定的區間是非負數，String的hashCode()方法卻會產生負數(不信用”192.168.1.0:1111″試試看就知道了)。不過這個問題好解決，取絕對值就是一種解決的辦法。

綜上，String重寫的hashCode()方法在一致性Hash算法中沒有任何實用價值，得找個算法重新計算HashCode。這種重新計算Hash值的算法有很多，比如CRC32_HASH、FNV1_32_HASH、KETAMA_HASH等，其中KETAMA_HASH是默認的MemCache推薦的一致性Hash算法，用別的Hash算法也可以，比如FNV1_32_HASH算法的計算效率就會高一些。

一致性Hash算法實現版本1：不帶虛擬節點

使用一致性Hash算法，盡管增強了系統的伸縮性，但是也有可能導致負載分布不均勻，解決辦法就是使用虛擬節點代替真實節點，第一個代碼版本，先來個簡單的，不帶虛擬節點。

下面來看一下不帶虛擬節點的一致性Hash算法的Java代碼實現：

/** * 不帶虛擬結點的一致性Hash算法 * @author 嘵嘵 * */public class ConsistentHashWithoutVN {? /** * 待加入Hash環的服務器列表 */ private static String[] servers = { "192.168.0.0:111