1，什么是算法的時間和空間復雜度

　　算法(Algorithm)是指用來操作數據，解決程序問題的一組方法，對于同一個問題，使用不同的算法，也許最終得到的結果是一樣的，但是在過程中消耗的資源和時間卻會有很大的區別。

　　那么我們應該如何去衡量不同算法之間的優劣呢？

　　主要還是從算法所占用的時間和空間兩個維度取考量。

• 時間維度：是指執行當前算法所消耗的時間，我們通常使用時間復雜度來描述。
• 空間維度：是指執行當前算法需要占用多少內存空間，我們通常用空間復雜度來描述

　　因此，評價一個算法的效率主要是看它的時間復雜度和空間復雜度情況，然而，有的時候時間和空間卻又是魚與熊掌，不可兼得，那么我們就需要從中去取一個平衡點。

　　下面分別學習一下時間復雜度和空間復雜度的計算方式。

1.1 時間復雜度

　　我們想要知道一個算法的時間復雜度，很多人首先想到的方法就是把這個算法程序運行一遍，那么它所消耗的時間就自然而然的知道了。這種方法可以嗎？當然可以，不過它也有很多弊端。

　　這種方式非常容易受運行環境的影響，在性能高的機器上跑出來的結果與在性能低的機器上跑的結果相差會很大。而且對測試時使用的數據規模也有很大關系。再者我們再寫算法的時候，還沒有辦法完整的去運行呢，因此，另一種更為通用的方法就出來了：大O符號表示法，即T(n) = O(f(n))。

　　我們先看一個例子：

for(i=1; i<=n; ++i){???j = i;???j++;}

　　通過大O符合表示法，這段代碼的時間復雜度為O(n)，為什么呢？

　　在大O符號表示法中，時間復雜度的公式是：T(n) = O( f(n) )，其中f(n)表示每行代碼執行次數之和，而O表示正比例關系，這個公式的全稱是：算法的漸進時間復雜度。

　　 我們繼續看上面的例子，假設每行代碼的執行時間都是一樣的，我們用1顆粒時間來表示，那么這個例子的第一行耗時是1個顆粒時間，第三行的執行時間是n個顆粒時間，第四行執行時間也是n個顆粒時間(第二行和第五航是符號，暫時忽略)，那么總時間就是1顆粒時間+n顆粒時間+n顆粒時間，即 T(n) = (1+2n)*顆粒時間，從這個結果可以看出，這個算法的耗時是隨著n的變化而變化，因此，我們可以簡化的將這個算法的時間復雜度表示為：T(n) = O(n)。

　　為什么可以這么去簡化呢，因為大O符號表示法并不是用于來真實代表算法的執行時間的，它是用來表示代碼執行時間的增長變化趨勢的。

　　所以上面的例子中，如果n無限大的時候，T(n) = time(1+2n)中的常量1就沒有意義了，倍數2也意義不大。因此直接簡化為T(n) = O(n) 就可以了。

常用的時間復雜度量級有：

• 常數階O(1)
• 對數階O(N)
• 線性階O(logN)
• 線性對數階O(nlogN)
• 平方階O(n2)
• 立方階O(n3)
• K 次方階O(n^k)
• 指數階(2^n)

　　從上之下依次的時間復雜度越來越大，執行的效率越來越低。

　　下面選取一些較為常用的來說一下。

1，常數階O(1)

　　無論代碼執行了多少行，只要是沒有循環等復雜結構，那這個代碼的時間復雜度就都是O(1)，如：

int?i = 1;int?j = 2;++i;j++;int?m = i + j;

　　上述代碼在執行的時候，它消耗的時候并不隨著某個變量的增長而增長，那么無論這類代碼有多長，即使有幾萬幾十萬行，都可以用O(1)來表示它的時間復雜度。

2，對數階O(N)

for(i=1; i<=n; ++i){???j = i;???j++;}

　　這段代碼，for循環里面的代碼會執行N遍，因此它消耗的時間是隨著n的變化而變化的，因此這類代碼都可以用O(n)來表示它的時間復雜度。

3，線性階O(logN)

　　先看代碼

int?i = 1;while(i

　　從上面代碼可以看到，在while循環里面，每次都將 i 乘以 2，乘完之后，i 距離 n 就越來越近了。我們試著求解一下，假設循環x次之后，i 就大于 2 了，此時這個循環就退出了，也就是說 2 的 x 次方等于 n，那么 x = log2^n　　也就是說當循環 log2^n 次以后，這個代碼就結束了。因此這個代碼的時間復雜度為：O(logn)

4，線性對數階O(nlogN)

　　線性對數階O(nlogN) 其實非常容易理解，將時間復雜度為O(logn)的代碼循環N遍的話，那么它的時間復雜度就是 n * O(logN)，也就是了O(nlogN)。

　　就拿上面的代碼加一點修改來舉例：

for(m=1; m

5，平方階O(n2)

　　平方階O(n2)更容易理解了，如果把 O(n) 的代碼再嵌套循環一遍，它的時間復雜度就是 O(n2) 了。　　舉例：

for(x=1; i<=n; x++){???for(i=1; i<=n; i++)????{???????j = i;???????j++;????}}

　　這段代碼其實就是嵌套了2層n循環，它的時間復雜度就是 O(n*n)，即 O(n2) 　　如果將其中一層循環的n改成m，即：

for(x=1; i<=m; x++){???for(i=1; i<=n; i++)????{???????j = i;???????j++;????}}

　　那它的時間復雜度就變成了 O(m*n)

6，立方階O(n3)及K 次方階O(n^k)

　　參考上面O(n2)去理解就好了，相當于三層n循環，其他的類似。

　　除此之外，其實還有 平均時間復雜度、均攤時間復雜度、最壞時間復雜度、最好時間復雜度 的分析方法，有點復雜，這里就不展開了。

1.2 空間復雜度

　　空間復雜度：用來評估算法內存占用大小的式子。

　　既然時間復雜度不是用來計算程序具體耗時的，那么我們也應該明白，空間復雜度也不是用來計算程序實際占用的空間的。空間復雜度是對一個算法在運行過程中臨時占用存儲空間大小的一個量度，同樣反映的是一個趨勢，我們用S(N)來定義。

　　空間復雜度的表示方式與時間復雜度完全一樣：

1. 算法使用了幾個變量：O(1)
2. 算法使用了長度為 n 的一維列表： O(n)
3. 算法使用了m 行 n 列的二維列表：O(mn)

　　空間復雜度比較常用的有：O(1)，O(n)，O(n2)，我們來看看：

空間復雜度O(1)

　　如果算法執行所需要的臨時空間不隨著某個變量n的大小而變化，即此算法空間復雜度為一個常量，可以表示為O(1)。

　　舉例：

int?i = 1;int?j = 2;++i;j++;int?m = i + j;

　　代碼中的i，j，m所分配的空間都不隨著處理數據量變化，因此他的空間復雜度S(n) = O(1)

空間復雜度O(n)

　　我們先看一個代碼：

int[] m =?new?int[n]for(i=1; i<=n; ++i){???j = i;???j++;}　　

這段代碼中，第一行new了一個數組出來，這個數據占用的大小為n，這段代碼的2~6行，雖然有循環，但是沒有再分配新的空間，因此，這段代碼的空間復雜度主要看第一行即可，即S(n)=O(n)。

空間換時間：常會為了追求時間復雜度而犧牲空間復雜度。

1.3 如何簡單快速的判斷算法復雜度

快速判斷算法復雜度(適用于絕大多數簡單情況)：

1. 確定問題規模 n
2. 循環減半過程 ——> logN
3. k層關于 n 的循環——> nk

復雜情況：根據算法執行過程判斷

2，常用的算法總結

2.1 遞歸

2.1.1 遞歸概念

　　遞歸的兩個特點：1:，調用自身 2，結束條件

　　舉個例子學習下面函數是不是遞歸：

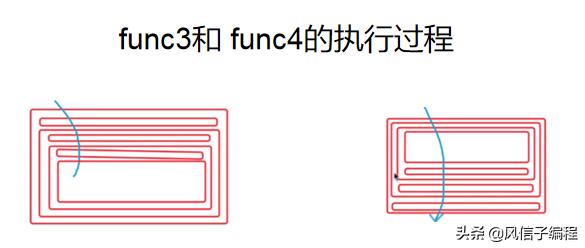
# 這個是一個死遞歸，只調用自身，但是沒有結束條件def func1(x):????print(x)????func1(x-1)?# 這個是一個死遞歸，看似有結束條件，但是卻無法結束def func2(x):????if?x > 0:????????print(x)????????func2(x+1)?# 這是一個遞歸函數,滿足調用自身，并且有結束條件def func3(x):????if?x > 0:????????print(x)????????func3(x-1)??# 這個也是一個遞歸，但是和func3有區別def func4(x):????if?x > 0:????????func4(x-1)????????print(x)

　　func3和func4的區別是什么？

　　假設x為3，那么func3輸出的結果為：3,2,1 而 func4輸出的結果為： 1,2,3。

　　為了方便理解，我們利用如下圖：

2.1.2 遞歸實例：漢諾塔問題

　　問題描述：大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從上往下按照大小順序摞著64片黃金圓盤。大梵天命名婆羅門把圓盤從下面開始按大小順序重新擺放在另一個柱子上。在小圓盤上不能放大圓盤，在三根柱子之間只能移動一個圓盤。64根柱子移動完畢之日，就是世界毀滅之時。

　　問題分析：

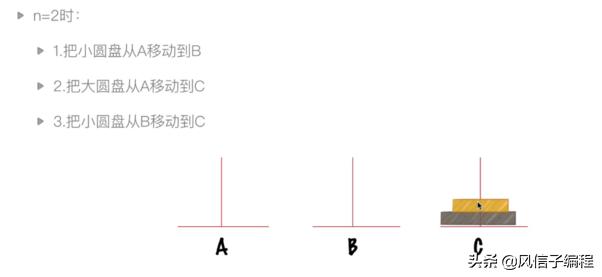
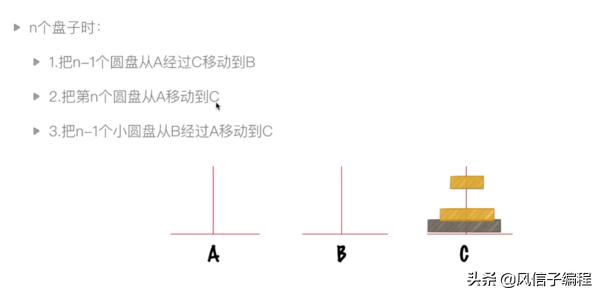
　　代碼實現：

def hanoi(x,a,b,c):????if?x>0:????????# 除了下面最大的盤子，剩下的盤子從a移動到b????????hanoi(x-1,a,c,b)????????# 把最大的盤子從a移到c????????print('%s->%s'%(a,c))????????# 把剩余的盤子從b移到c????????hanoi(x-1,b,a,c)??hanoi(3,'A','B','C')??# 計算次數def cal_times(x):????num = 1????for?i?in?range(x-1):????????# print(i)????????num = 2*num +1????print(num)??cal_times(3)

　　遞歸總結：

• 1，漢諾塔移動次數的遞推式： h(x) = 2h(x-1)+1
• 2，h(64) = 18446744073709551615
• 3，假設婆羅門每秒鐘搬一個盤子，則總共需要 5800億年

　證明：為什么漢諾塔的計算次數是2n+1呢？

　　對于一個單獨的塔，可以進行以下操作：

• 1：將最下方的塔的上方的所有塔移動到過渡柱子
• 2：將底塔移動到目標柱子
• 3：將過渡柱子上的其他塔移動到目標柱子

所以f(3)=f(2)+1+f(2)=7然后以此類推

• f(4)=f(3)+1+f(3)=15
• f(5)=f(4)+1+f(4)=31
• f(6)=f(5)+1+f(5)=63
• f(7)=f(6)+1+f(6)=127
• f(8)=f(7)+1+f(7)=255
• f(9)=f(8)+1+f(8)=511

　　f(x+1)=2*f(x)+1再進一步，可以得到通項公式為　　f(x)=2^x-1

2.2 查找算法

　　查找：在一些數據元素中，通過一定的方法找出與給定關鍵字相同的數據元素的過程。

　　列表查找(線性表查找)：從列表中查找指定元素

1. 輸入：列表，待查找元素
2. 輸出：元素下標(未找到元素時一般返回None或 -1)

內置列表查找函數：index()

2.2.1 順序查找(Linear Search)

　　順序查找：也叫線性查找，從列表第一個元素開始，順序進行搜索，直到找到元素或搜索到列表最后一個元素為止。

　　時間復雜度為：O(n)

def linear_search(data_set, value):????for?i?in?data_set:????????if?value == data_set[i]:????????????return?i????return?None

2.2.2 二分查找(Binary Search)

　　二分查找：又叫折半查找，從有序列表的初始候選區 li[0:n] 開始，通過對待查找的值與候選區中間值得比較，可以使候選區減少一半。

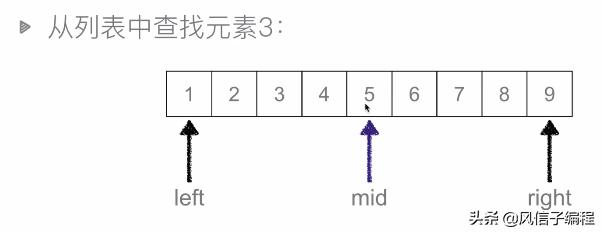
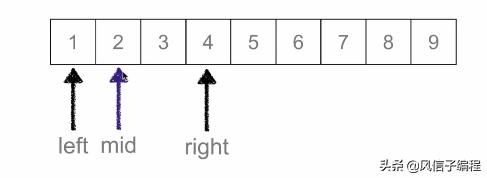
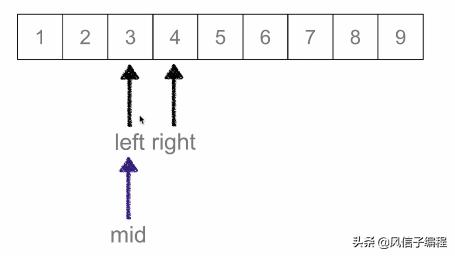
　　時間復雜度：O(logN)

def binary_search(data_list, val):???????low = 0???????????????????????? # 最小數下標???????high = len(data_list) - 1?????? # 最大數下標???????while?low <= high:???????????????mid = (low + high)?// 2???? # 中間數下標???????????????if?data_list[mid] == val:?? # 如果中間數下標等于val, 返回???????????????????????return?mid???????????????elif data_list[mid] > val:? # 如果val在中間數左邊, 移動high下標???????????????????????high = mid - 1???????????????else:?????????????????????? # 如果val在中間數右邊, 移動low下標???????????????????????low = mid + 1????else:???????????return?None??? # val不存在, 返回None?ret = binary_search(list(range(1, 10)), 3)print(ret)

2.3 列表排序算法

　　排序：將一組“無序”的記錄序列調整為“有序” 的記錄序列。

　　列表排序：將無序列表變為有序列表

• 輸入：列表
• 輸出：有序列表

　　升序與降序

　　內置排序算法：sort()

2.3.1 常見排序算法

　　如下圖所示：

　　部分排序算法的時間復雜度和空間復雜度及其穩定性如下：

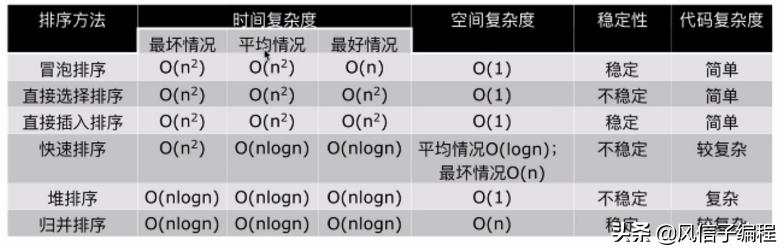
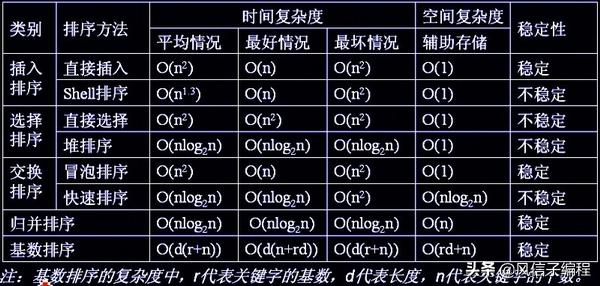
2.3.2 冒泡排序(Bubble Sort)

　　冒泡排序：像開水燒氣泡一樣，把最大的元素冒泡到最上面。一趟就是把最大的冒到最上面。冒到最上面的區域叫有序區。下面叫無序區。

　　列表每兩個相鄰的數，如果前面比后面大，則交換這兩個數。

　　一趟排序完成后，則無序區減少一個數，有序區增加一個數。

　　代碼關鍵點：趟，無序區范圍

　　時間復雜度：O(n2)

def bubble_sort(li):????for?i?in?range(len(li)-1):????????for?j?in?range(len(li)-1-i):????????????if?li[j] > li[j+1]:????????????????li[j], li[j+1] = li[j+1], li[j]????return?li

　　冒泡排序降序排列：

# 降序排列import random?def bubble_sort(li):????for?i?in?range(len(li)-1):? # 第 i 趟????????for?j?in?range(len(li)-1-i):????????????if?li[j] < li[j+1]:????????????????li[j], li[j+1] = li[j+1], li[j]?li = [random.randint(0, 10)?for?i?in?range(10)]print(li)bubble_sort(li)print(li)'''[5, 2, 10, 5, 5, 2, 5, 4, 3, 2][10, 5, 5, 5, 5, 4, 3, 2, 2, 2]'''

　 當然也可以打印每一趟，看看冒泡排序的過程：

# 升序排列，打印每一趟，看看其過程def bubble_sort(li):????for?i?in?range(len(li)-1):? # 第 i 趟????????for?j?in?range(len(li)-1-i):????????????if?li[j] > li[j+1]:????????????????li[j], li[j+1] = li[j+1], li[j]????????print(li)?li = [9,8,7,6,5,4,3,2,1]print('origin:',li)bubble_sort(li)?'''origin: [9, 8, 7, 6, 5, 4, 3, 2, 1][8, 7, 6, 5, 4, 3, 2, 1, 9][7, 6, 5, 4, 3, 2, 1, 8, 9][6, 5, 4, 3, 2, 1, 7, 8, 9][5, 4, 3, 2, 1, 6, 7, 8, 9][4, 3, 2, 1, 5, 6, 7, 8, 9][3, 2, 1, 4, 5, 6, 7, 8, 9][2, 1, 3, 4, 5, 6, 7, 8, 9][1, 2, 3, 4, 5, 6, 7, 8, 9]'''

　　冒泡排序的最差情況，即每次都交互順序的情況下，時間復雜度為O(n**2)。

　　存在一個最好情況就是列表本來就是排好序，所以可以加一個優化，也就是一個標志位，如果沒有出現交換的情況，說明列表已經有序，可以直接結束算法，則直接return。

def optimize_bubble_sort(li):????for?i?in?range(len(li)-1):????????exchange = False????????for?j?in?range(len(li)-1-i):????????????li[j],li[j+1] = li[j+1],li[j]????????????exchange =True????????if?not exchange:????????????return?li????return?li

2.3.3 選擇排序(Select Sort)

　　一趟排序記錄最小的數，放到第一個位置

　　再一趟排序記錄記錄列表無序區最小的數，放到第二個位置。。。。

　　算法的關鍵點：有序區和無序區，無序區最小數的位置。

　　先看一個簡單的選擇排序

def select_sort_simple(li):????li_new = []????for?i?in?range(len(li)):????????min_val = min(li)????????li_new.append(min_val)????????li.remove(min_val)????return?li_newli = [4,3,2,1]print(select_sort_simple(li))# [1, 2, 3, 4]

　　我們會發現首先他生成了兩個列表，那么就占用了兩份內存，而算法的思想則是能省則省，能摳則摳，所以我們需要改進一下。

def select_sort(li):????for?i?in?range(len(li)-1):? # i 是第幾趟????????min_loc = i????????for?j?in?range(i+1, len(li)):????????????if?li[j] < li[min_loc]:????????????????min_loc = j????????li[i], li[min_loc] = li[min_loc], li[i]????return?li?li = [1,2,3,4]print(select_sort(li))# [1, 2, 3, 4]

2.3.4 插入排序(Insertion Sort)

　　原理：把列表分成有序區和無序區兩個部分。最初有序區只有一個元素。然后每次從無序區選擇一個元素，插入到有序區的位置，直到無序區變空。

def insert_sort(li):????for?i?in?range(1, len(li)):? # i表示摸到的牌的下標????????temp = li[i]????????j = i - 1? # j指的時手里的牌的下標????????# if j > 0 and temp < li[j]:? # 找到一個合適地位置插進去????????while?j >= 0 and li[j] > temp:????????????li[j + 1] = li[j]????????????j -= 1????????li[j + 1] = temp????return?li

　　簡單形象的一張圖：

　　時間復雜度是 O(n2)

　　如果目標是 n 個元素的序列升序排列，那么采用插入排序存在最好情況和最壞的情況。最好情況就是，序列已經是升序排列了，在這種情況下，需要進行的比較操作需要(n-1)次即可。最壞的情況就是序列是降序排列，那么此時需要進行的比較共有 n(n-1)/2次。插入排序的賦值操作時比較操作的次數加上 (n-1)次。平均來說插入排序算法的時間復雜度為O(n^2)，因而插入排序不適合對于數據量比較大的排序應用。但是，如果需要排序的數據量很小，例如量級小于千，那么插入排序還是一個不錯的選擇。

2.3.5 快速排序

　　原理：讓指定的元素歸位，所謂歸位，就是放到他應該放的位置(左邊的元素比他小，右邊的元素比他大)，然后對每個元素歸位，就完成了排序。

　　可以參考下面動圖來理解代碼：

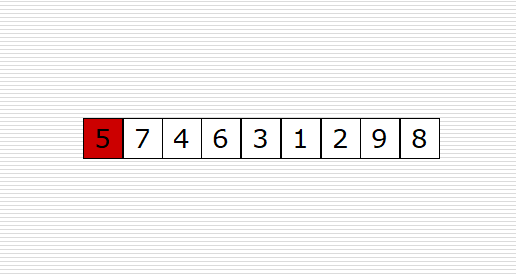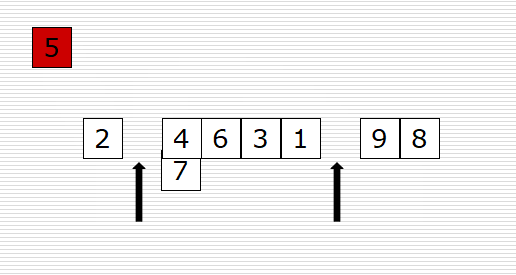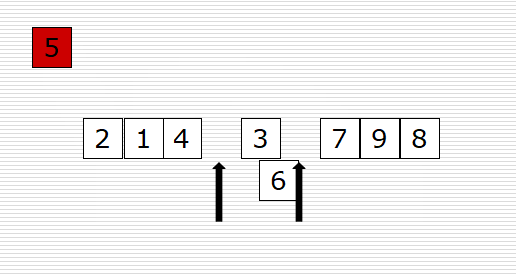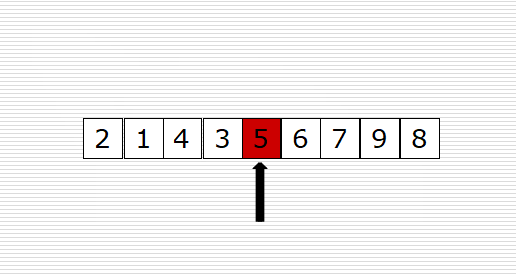
　　左邊空位置，從右邊找，右邊空位置，從左邊找。當左邊和右邊重合的時候，就是mid。

　　　　下圖來自百度百科

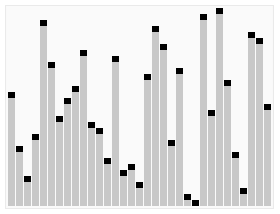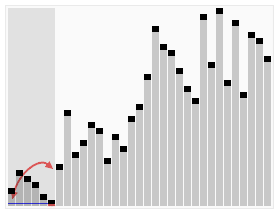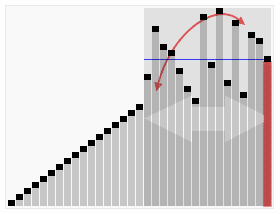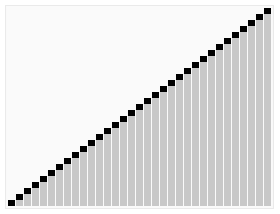
　　快速排序——框架函數

def quick_sort(data, left, right):????if?left < right:????????mid = partition(data, left, right)????????quick_sort(data, left, mid-1)????????quick_sort(data, mid+1, right)

　　完整代碼如下：

def partition(data, left, right):????# 把左邊第一個元素賦值給tmp，此時left指向空????tmp = data[left]????# 如果左右兩個指針不重合，則繼續????while?left < right:????????while?left < right and data[right] >= tmp:????????????right -= 1?? # 右邊的指標往左走一步????????# 如果right指向的元素小于tmp，就放到左邊目前為空的位置????????data[left] = data[right]????????print('left:', li)????????while?left < right and data[left] <= tmp:????????????left += 1????????# 如果left指向的元素大于tmp，就交換到右邊目前為空的位置????????data[right] = data[left]????????print('right:', li)????data[left] = tmp????return?left??# 寫好歸位函數后，就可以遞歸調用這個函數，實現排序def quick_sort(data, left, right):????if?left < right:????????# 找到指定元素的位置????????mid = partition(data, left, right)????????# 對左邊的元素排序????????quick_sort(data, left, mid - 1)????????# 對右邊的元素排序????????quick_sort(data, mid + 1, right)????return?data??li = [5, 7, 4, 6, 3, 1, 2, 9, 8]print('start:', li)partition(li, 0, len(li) - 1)print('end:', li)?'''start: [5, 7, 4, 6, 3, 1, 2, 9, 8]left: [2, 7, 4, 6, 3, 1, 2, 9, 8]right: [2, 7, 4, 6, 3, 1, 7, 9, 8]left: [2, 1, 4, 6, 3, 1, 7, 9, 8]right: [2, 1, 4, 6, 3, 6, 7, 9, 8]left: [2, 1, 4, 3, 3, 6, 7, 9, 8]right: [2, 1, 4, 3, 3, 6, 7, 9, 8]end: [2, 1, 4, 3, 5, 6, 7, 9, 8]'''

　　正常的情況，快排的復雜度是O(nlogn)

　　快排存在一個最壞情況，就是每次歸位，都不能把列表分成兩部分，此時復雜度就是O(n2)了，如果要避免設計成這種最壞情況，可以在取第一個數的時候不要取第一個了，而是取一個列表中的隨機數。

2.3.6 堆排序(Heap Sort)

　　本質是使用大根堆或小根堆來對一個數組進行排序。所以首先要理解樹的概念。

　　關于樹的理解請參考博客：https://www.cnblogs.com/wj-1314/p/11631934.html

　　堆簡單來說：一種特殊的完全二叉樹結構

• 大根堆：一種完全二叉樹，滿足任一節點都比其孩子節點大
• 小根堆：一種完全二叉樹，滿足任一節點都比其孩子節點小

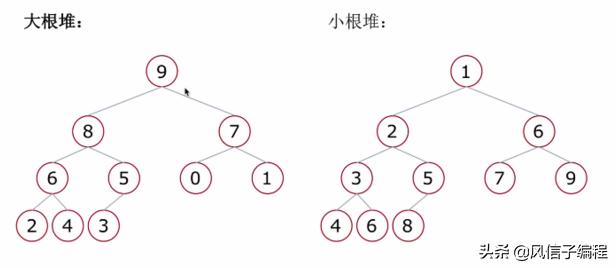
堆排序——堆的向下調整性質

　　假設根節點的左右子樹都是堆，但根節點不滿足堆的性質，可以通過一次向下的調整來將其變成一個堆

　　當根節點的左右子樹都是堆時，可以通過一次向下的調整來將其變換成一個堆。

堆排序過程

1，建立堆

2，得到堆頂元素，為最大元素

3，去掉堆頂，將堆最后一個元素放到堆頂，此時可以通過一次調整重新使堆有序。

4，堆頂元素為第二大元素

5，重復步驟3，直到堆變為空

　　代碼如下：

def sift(data, low, high):????i = low????j = 2*i+1????tmp = data[i]????while?j <=high:????????if?j < high and data[j] < data[j+1]:????????????j+=1????????if?tmp < data[j]:????????????data[i] = data[j]????????????i = j????????????j = 2*i+1????????else:????????????break????data[i] = tmp?def heap_li(li):????n = len(li)????for?i?in?range((n - 2)?// 2, -1, -1):????????# i表示建堆的時候調整的部分的跟的下標????????sift(li, i, n - 1)????# 建堆完成了????print('建堆完成后的列表：',li)????for?i?in?range(n-1, -1, -1):????????# i 指向當前堆的最后一個元素????????li[0], li[i] = li[i], li[0]????????sift(li, 0, i-1)? # i-1是新的high????print(li)?li = [i?for?i?in?range(12)]import randomrandom.shuffle(li)print(li)?heap_li(li)print(li)'''[7, 2, 4, 3, 8, 9, 0, 5, 11, 6, 10, 1]建堆完成后的列表： [11, 10, 9, 5, 8, 4, 0, 2, 3, 6, 7, 1][0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11][0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]'''

堆排序應用——topK問題

　　問題描述：現在有n個數，設計算法得到前k大的數( k

　　解決思路：

1. 排序后切片 時間復雜度為：O(nlogn)
2. 排序(選擇，插入，冒泡) 時間復雜度為：O(mn)
3. 堆排序思路 時間復雜度為：O(mlogn)

　　代碼如下：

def sift(li, low, high):????i = low????j = 2 * i + 1????tmp = li[low]????while?j <= high:????????if?j + 1 <= high and li[j + 1] < li[j]:????????????j = j + 1????????if?li[j] < tmp:????????????li[i] = li[j]????????????i = j????????????j = 2 * j + 1????????else:????????????break????????li[i] = tmp??def topk(li, k):????heap = li[0:k]????for?i?in?range((k - 2)?// 2, -1, -1):????????sift(heap, i, k - 1)????# 1,建堆????for?i?in?range(k, len(li) - 1):????????if?li[i] > heap[0]:????????????heap[0] = li[i]????????????sift(heap, 0, k - 1)????# 2，遍歷????for?i?in?range(k - 1, -1, -1):????????heap[0], heap[i] = heap[i], heap[0]????????sift(heap, 0, i - 1)????# 3，出數????return?heap??import random?li = list(range(1000))random.shuffle(li)print(topk(li, 10))

2.3.7 歸并排序(Merge Sort)

　　歸并：假設現在的列表分兩段有序，如何將其合成為一個有序列表，這種操作叫做一次歸并。

　　如下圖所示：虛線分開，兩個箭頭分別指向列表的第一個元素。然后從左邊開始比較兩邊的元素，小的出列。然后繼續循環，這樣就排出來一個有序列表。

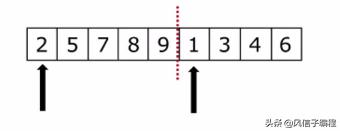
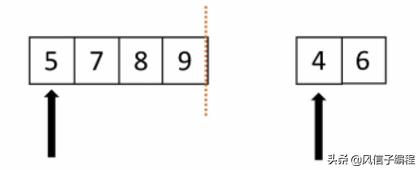
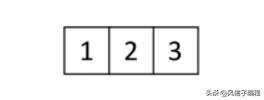
　　應用到排序就是把列表分成一個元素一個元素的，一個元素當然是有序的，將有序列表一個一個合并，列表越來越大，最終合并成一個有序的列表。

　　歸并排序如圖所示：

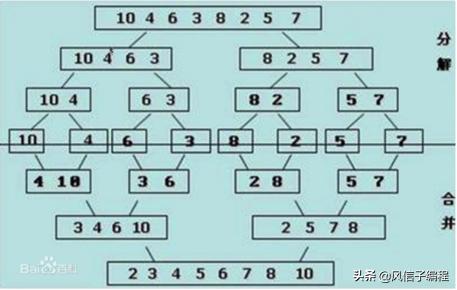
　　歸并排序代碼如下：

def merge(li, low, mid, high):????i = low? # i為左邊列表開頭元素的坐標????j = mid + 1? # j為右邊列表開頭元素的坐標????ltmpd = []? # 臨時列表????# 只要兩邊都有數????while?i <= mid and j <= high:????????if?li[i] < li[j]:????????????ltmpd.append(li[i])????????????i += 1????????else:????????????ltmpd.append(li[j])????????????j += 1????# while執行完，肯定有一部分沒數字了，就是兩個箭頭肯定有一個指向沒數了????while?i <= mid:????????ltmpd.append(li[i])????????i += 1????while?j <= high:????????ltmpd.append(li[j])????????j += 1????li[low:high + 1] = ltmpd????# return ltmpd???def merge_sort(li, low, high):????if?low < high:? # 列表中至少兩個元素，遞歸????????mid = (low + high)?// 2????????merge_sort(li, low, mid)????????merge_sort(li, mid + 1, high)????????merge(li, low, mid, high)?li = list(range(10))import randomrandom.shuffle(li)print(li)merge_sort(li, 0, len(li)-1)print(li)

　　歸并排序的時間復雜度：O(nlogn)

　　歸并排序的空間復雜度：O(n)

2.3.8 快速排序，堆排序，歸并排序三種算法的總結

1，三種排序算法的時間復雜度都是O(nlogn)

2，一般情況下，就運行時間而言：快速排序 < 歸并排序 < 堆排序

3，三種排序算法的缺點

• 快速排序：極端情況下排序效率低
• 歸并排序：需要額外的內存開銷
• 堆排序：在快的排序算法中相對較慢

2.3.9 希爾排序(Shell Sort)

　　希爾排序(Shell Sort)是一種分組插入排序算法。

　　其算法步驟如下：

• 首先取一個整數 d1=n/2，將元素分為 d1個組，每組相鄰量元素之間距離為 d1，在各組內進行直接插入排序；
• 然后取第二個整數 d2=d1/2，重復上述分組排序過程，知道 di=1，即所有元素在同一組內進行直接插入排序；
• 最后希爾排序每趟并不使某些元素有序，而是使整體數據越來越接近有序，最后一趟排序使得所有數據有序

　　圖解如下：

　　1，數組(列表)如下：

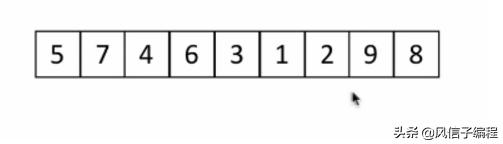
　　 2，d=4(即d=len(li)/2):

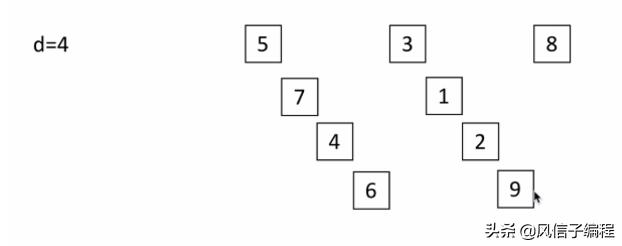
　　3，d=2：

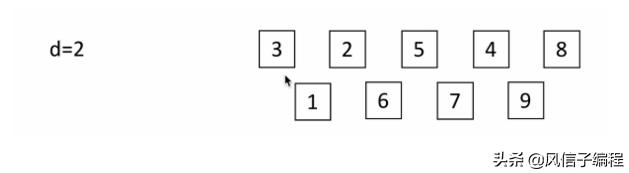
　　 4，d=1：

　　在wiki查找地址如下：https://en.wikipedia.org/wiki/Shellsort#Gap_sequences

　　希爾排序的時間復雜度討論比較復雜，并且和選取的gap序列有關。

2.3.10 計數排序(Count Sort)

　　簡單來說如下圖所示：

　　出現那個數，就給那個數的數量加一。

　　代碼如下：

def count_sort(li, max_count=100):????count = [0?for?_?in?range(max_count+1)]????for?val?in?li:????????count[val] += 1????li.clear()? # 原列表清空，這樣就不用建新列表，省內存????for?ind, val?in?enumerate(count):????????for?i?in?range(val):????????????li.append(ind)?import randomli = [random.randint(0, 19)?for?_?in?range(30)]print(li)count_sort(li)print(li)'''[1, 4, 13, 6, 19, 4, 9, 14, 10, 15, 7, 1, 1, 9, 3, 8, 17, 3, 18, 1, 8, 17, 14, 2, 10, 0, 5, 8, 12, 15][0, 1, 1, 1, 1, 2, 3, 3, 4, 4, 5, 6, 7, 8, 8, 8, 9, 9, 10, 10, 12, 13, 14, 14, 15, 15, 17, 17, 18, 19]'''

　　對列表進行排序，已知列表中的數范圍都在0到100之間，設計時間復雜度為O(n)的算法。就可以使用此算法，即使列表長度大約為100萬，雖然列表長度很大，但是數據量很小，會有大量的重復數據，我們可以考慮對這100個數進行排序。

2.3.11 桶排序(Bucket Sort)

　　桶排序也叫計數排序，簡單來說，就是將數據集里面所有元素按順序列舉出來，然后統計元素出現的次數，最后按照順序輸出數據集里面的元素。

　　在計數排序中，如果元素的范圍比較大(比如在1到1億之間)，如何改造算法？

　　桶排序(Bucket Sort)：首先將元素分在不同的桶中，在對每個桶中的元素排序。

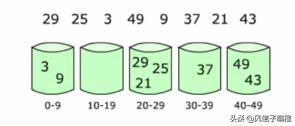
　　如上圖，列表為 [29, 25, 3, 49, 9, 37, 21, 43]排序，我們知道數組的范圍是0~49，我們將其分為5個桶，然后放入數字，一次對桶中的元素排序。

　　桶排序的表現取決于數據的分布。也就是需要對不同數據排序采取不同的分桶策略。

• 平均情況時間復雜度為：O(n+k)
• 最壞情況時間復雜度為：O(n2k)
• 空間復雜度為：O(nk)

　　代碼如下：

#_*_coding:utf-8_*_?def bucket_sort(li, n=100, max_num=10000):????buckets = [[]?for?_?in?range(n)]? # 創建桶????for?var?in?li:????????# 0 -》 0， 86????????i = min(var?// (max_num // n), n-1)? # i表示var放到幾號桶里????????buckets[i].append(var)? # 把var加入到桶里????????# [0, 2, 4]????????# 保持桶內的順序????????for?j?in?range(len(buckets[i])-1, 0, -1):????????????if?buckets[i][j] < buckets[i][j-1]:????????????????buckets[i][j], buckets[i][j-1] = buckets[i][j-1], buckets[i][j]????????????else:????????????????break?????sorted_li = []????for?buc?in?buckets:????????sorted_li.extend(buc)????return?sorted_li?import randomif?__name__ ==?'__main__':????li = [random.randint(0, 10000)?for?i?in?range(10000)]????# print(li)????li = bucket_sort(li)????print(li)

2.3.12 基數排序

　　多關鍵字排序：加入現在有一個員工表，要求按照薪資排序，年齡相同的員工按照年齡排序。

　　方法：先按照年齡進行排序，再按照薪資進行穩定的排序。

　　比如對 [32, 13, 94, 52, 17, 54, 93] 排序是否可以看成多關鍵字排序？

　　實現示例如下：

　　1，首先按照個位分桶：

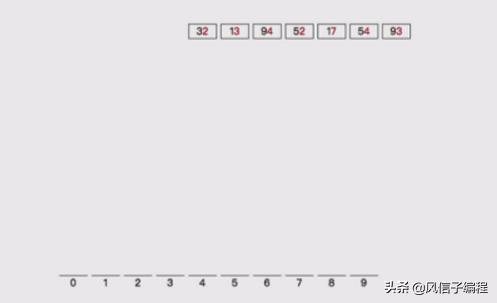
　　2，按照個位數分好,桶，然后擺回原位

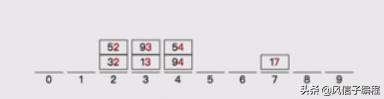
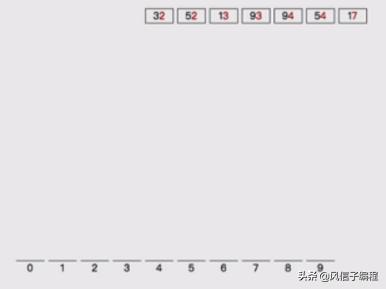
　　3，按照十位數進行分桶，然后將桶里的數排序

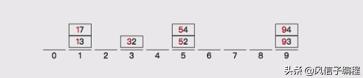
　　基數排序是一種非比較型整數排序算法，其原理是將整數按位數切割成不同的數字，然后按照每個位數分別比較。由于整數也可以表達字符串(比如名稱或日期)和特定格式的浮點數，所以基礎排序也不是只能使用于整數。

　　基數排序的時間復雜度為：O(kn)

　 基數排序的空間復雜度為：O(k+n)

　　基數排序中 k 表示數字位數

　　 　　由于基數排序使用了桶排序，所以空間復雜度和桶排序的空間復雜度是一樣的。

　　代碼如下：

def list_to_buckets(li,?base, iteration):????buckets = [[]?for?_?in?range(base)]????for?number?in?li:????????digit = (number?// (base ** iteration)) % base????????buckets[digit].append(number)????return?buckets?def buckets_to_list(buckets):????return?[x?for?bucket?in?buckets?for?x?in?bucket]?def radix_sort(li,?base=10):????maxval = max(li)????it = 0????while?base?** it <= maxval:????????li = buckets_to_list(list_to_buckets(it,?base, it))????????it += 1????return?li

2.3.13 基數排序 VS 計數排序 VS 桶排序

　　這三種排序算法都利用了桶的概念，但對于桶的使用方法上有明顯差異。

• 基數排序：根據鍵值的每位數字來分配桶
• 計數排序：每個桶只存儲單一鍵值
• 桶排序：每個桶存儲一定范圍內的數值

三，幾道查找排序習題

　　這一節是對前面學習的算法的應用，也就是習題練習。

1，給兩個字符串s和t，判斷 t是否為s的重新排列后組成的單詞

　　s = 'anagram' t='nagaram' return true

　　s='rat', t='car', return false

　　兩種方法一種直接使用Python的list排序，當然這種時間復雜度可能高一些。另一種方法使用字典記錄list中出現字母的次數。代碼如下：

def isAnagram0(s, t):????return?sorted(list(s)) == sorted(list(t))def isAnagram1(s, t):????dict1 = []? # ['a':1,?'b':2]????dict2 = []????for?ch?in?s:????????dict1[ch] = dict1.get(ch, 0) + 1?????for?ch?in?t:????????dict2[ch] = dict2.get(ch, 0) + 1????return?dict1 == dict2

2，給定一個 m*n 的二維列表，查找一個數是否存在，列表有下列特性：

• 每一行的列表從左到右已經排序好
• 每一行第一個數比上一行最后一個數大

　　思路如下：有兩個方法，第一個是暴力遍歷法，但是這種時間復雜度會很高，而相對來說改進的方法是二分查找。

　　實現代碼如下：

def searchMatrix(matrix, target):????for?line?in?matrix:????????if?target?in?line:????????????return?True????return?False??def searchMatrix1(matrix, target):????h = len(matrix)????if?h == 0:????????return?False? # h=0 即為 []????# 當然也出現一種可能就是 [[],[]]????w = len(matrix[0])????if?w == 0:????????return?False????left = 0????right = w * h - 1????# 直接使用二分查找的代碼????while?left <= right:????????mid = (left + right)?// 2????????i = mid?// w????????j = mid % w????????if?matrix[i][j] == target:????????????return?True????????elif matrix[i][j] > target:????????????right = mid - 1????????else:????????????left = mid + 1????else:????????return?False??matrix = [[1, 2, 3], [5, 6, 7], [9, 12, 23]]target = 32res = searchMatrix1(matrix, target)print(res)

3，給定一個列表和一個整數，設計算法找到兩個數的下標，使得兩個數之和為給定的整數。保證肯定僅有一個結果。例如，列表[1,2,5,4] 與目標整數3,1+2=3，結果為(0,1)

　　代碼如下：

def TwoSum(nums, target):????'''?????:param nums:? nums是代表一個list????:param target: target是一個數????:return: 結果返回的時兩個數的下標????'''????for?i?in?range(len(nums)):????????for?j?in?range(i + 1, len(nums)):????????????if?nums[i] + nums[j] == target:????????????????return?(i, j)??def TwoSum1(nums, target):????# 新建一個空字典用來保存數值及在其列表中對應的索引????dict1 = {}????for?i?in?range(len(nums)):????????# 相減得到另一個數值????????num = target - nums[i]????????if?num not?in?dict1:????????????dict1[nums[i]] = i????????# 如果在字典中則返回????????else:????????????return?[dict1[num], i]?def binary_search(li,left, right, val):????while?left <= right: # 候選區有值????????mid = (left + right)?// 2????????if?li[mid] == val:????????????return?mid????????elif li[mid] < val:????????????left = mid +1????????else:????????????right = mid -1????else:????????return?None?def TwoSum2(nums, target):????for?i?in?range(len(nums)):????????a = nums[i]????????b = target - a????????if?b >=a:????????????j = binary_search(nums, i+1, len(nums)-1, a)????????else:????????????j = binary_search(nums, 0, i-1, b)????????return?(i, j)