一、?課題的確定

學生在三年級學過長方形、正方形的面積計算，經歷過從數方格的辦法得出面積計算公式的過程。因此，學生對于面積計算公式的推導有一定的經驗和知識基礎。基于上述考慮，我想完全放手讓學生去研究如何計算平行四邊形的面積。這對學生來說顯然是一個極大挑戰，他們會怎么研究呢？我忐忑不安又充滿期待。

二、?課題的布置與指導

1、第一天

面向全體學生布置研究任務：平行四邊形的面積怎樣計算？(要求學生不能看課本，不能上網查資料，也不能問家長，只能自己研究。)

2、第二天

收集學生的研究成果，發現學生的研究成果有以下幾種：(1)平行四邊形的面積等于兩條鄰邊相乘，這種意見占了一大半；(2)平行四邊形的面積等于底乘高，全班只有5位同學得到這個結果。沒有同學去用數方格的方法去求平行四邊形的面積，大概嫌太麻煩吧。

對于提出平行四邊形的面積=鄰邊×鄰邊的同學，我建議他們不能只猜測，必須證明，讓所有的人信服。

3、第三天

多數同學證明平行四邊形的面積不等于鄰邊×鄰邊，應等于底乘高，有一位同學提出平行四邊形的面積等于高乘高，有一位同學還堅持平行四邊形的面積等于鄰邊×鄰邊。我只好引導他用數方格的方法證明看看。當他數完后果然發現，不能用鄰邊×鄰邊計算平行四邊形面積。我把這位同學留在辦公室里，觀察他的研究思路，他冥思苦想了兩個小時，卻沒有一點眉目，我只好讓他在方格紙上畫了很多底相等，高不同的平行四邊形，讓他反復觀察、數出面積，找到面積與什么有關，又經過3個多小時的努力，終于很疑惑的問我：“平行四邊形的面積是不是與它的高和底有關？”我說：“對，你的猜測很準確，你再畫兩個高和底都相等的長方形和平行四邊形，會發現什么？”只用了半個小時，他就很驚喜的告訴我：高和底都相等，長方形和平行四邊形面積相等，所以平行四邊形面積=底×高。

4、第四天

大多數同學都能證明平行四邊形面積=底×高，他們證明的方法不同，好多方法是在我們正常的40分鐘課堂從來沒有出現過的，任何參考資料上都沒有的。

三、課堂精彩片段

師：孩子們，偉大的科學家牛頓說過，“沒有大膽的猜想，就沒有偉大的發現”。這次，我們研究平行四邊形的面積正是從大膽的猜想啟航的。下面我們請二組的同學展示他們的研究成果。

曹原：大家還記得嗎？長方形的面積等于什么？正方形的面積等于什么？長方形和正方形的面積都是鄰邊×鄰邊。我就想：平行四邊形的面積是否也等于鄰邊×鄰邊？

我把兩根長小棒和兩根短小棒拼在一起，成了一個長方形，再把它稍微拉動了一下，成了一個平行四邊形。它的面積跟原來差不多。“可是，”我又繼續朝著同一個方向拉伸，“可是如果它已經不是原來的樣子，而是這個樣子了，面積都快成一條縫了，怎么會和先前長方形的面積一樣呢？”于是用鄰邊×鄰邊的方法去求平行四邊形的面積是錯誤的。

師：三組的同學對這個問題也做了深入的研究，看他們研究的方法是否一樣。

周冠妤：平行四邊形的面積是否等于鄰邊×鄰邊，我做了一個平行四邊形的框架，這樣它們的邊不變，就可以拉出不同形狀的平行四邊形。

我把長方形描在方格本上，又拉了幾個不同的平行四邊形，也描在方格本上，數了數圖形1的面積是70個方格，圖形2的面積是50個方格，圖形3的面積是38個方格，圖形4的面積是26個方格，平行四邊形的面積越來越小。如圖：

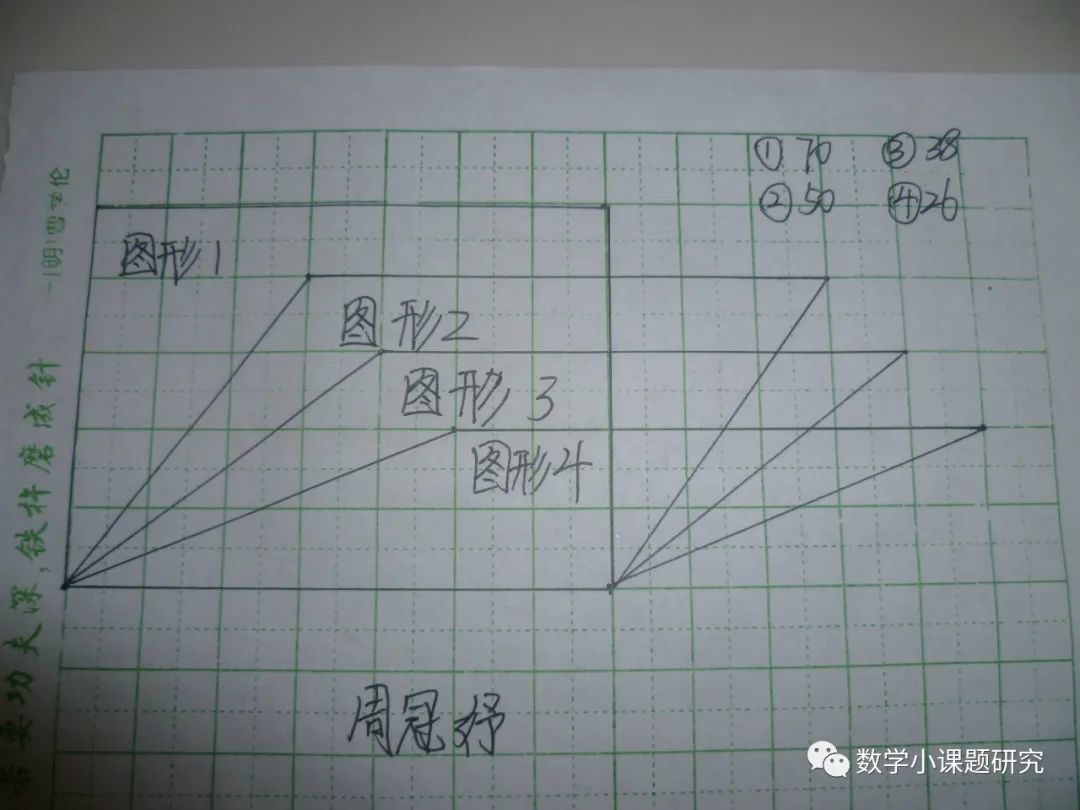
我的結論得出來了，事實證明：計算平行四邊形的面積是不能用鄰邊×鄰邊這種方法的。我的匯報完畢，謝謝大家。

師：孩子們，看來面對同一個問題，每人開啟智慧的方式是不一樣的，一組同學用事實、畫圖說話，而另一組同學用數據說話，這都是我們證明科學問題常用的方法，值得借鑒。

師：有同學猜想：平行四邊形的面積=高×高，是否這樣呢？請一組的同學給我們展示。

呂芃霖：我開始認為平行四邊形的面積應該是高×高，因為長方形的兩條高就是長和寬。于是我就畫了一個以兩條高為邊的長方形數了數，可是只有7.5個格，而我數了數原來平行四邊形有15個格，看來平行四邊形的面積不等于高×高。

師：看來還是不對，研究科學就是這樣，需要我們不斷地猜想、驗證、否定，不斷產生新的想法，不斷前進，于是我們離真理越來越近。有同學猜想：平行四邊形的面積=底×高，先請二組同學展示他們是如何研究這個問題的。

張瑞林：我們用的是“變形法”。昨上，我坐在竹席上思考平行四邊形面積到底怎么計算，我忽然眼前一亮，竹席是由長短、粗細一樣竹條編成的，如果把竹條編成平行四邊形，它的面積會發生變化嗎？我馬上找來小棒代替竹條做實驗。

我先用32根小棒拼成了長方形，又用32根小棒編成了平行四邊形，大家說拼成平行四邊形和長方形的面積有沒有發生變化？

生：沒有發生變化。

張瑞林：大家再仔細觀察，還有什么沒有發生變化？

生：小棒長短沒有變化

張瑞林：小棒長短沒有變化說明底相同，對嗎？

生：小棒的數量沒有發生變化。

張瑞林：小棒疊加起來的高度是平行四邊形的高。

因為長方形的面積=長×寬，所以平行四邊形的面積=底×高。

如果排成別的樣子也會這樣嗎？我又排了很多形狀，如箭頭形、弧形、波浪形，我把它們排在一起，大家看，他們的面積是不是還是沒有發生變化？還有設么沒有發生變化？

生：小棒的長短和數量都沒發生變化。

張瑞林：也就是組成的圖形的底和高沒有發生變化，由此我們可以推斷：底高相等，上下粗細一樣的圖形，都可以用底乘高來計算面積。不管側邊有多長，都與面積沒有關系。如下圖：

張瑞林：還有不明白的地方嗎？

生：可是長方形沒有底和高啊。

張瑞林：長方形的長就是它的底，長方形的寬就是它的高，只不過是換了個說法而已。明白了嗎？

生：我明白了。

師：很好，舉一反三，不但得到一種圖形的面積，還得到一類圖形的面積，同時，這些同學的研究給了我們很好的啟示：面是由線構成的，線是有點構成的，而面疊加起來又可以構成我們周圍的立體世界，如，這本書由許多長方形構成的。以小積大，怪不得古人云：不積跬步，無以至千里，不積小流，無以成江海。希望同學們在生活和學習中積跬步，積小流，成大器。

師：一組也研究出了平行四邊形的面積=底×高，請他們展示研究成果。

李藝瑩：我先畫出平行四邊形，因為我們學過，平行四邊形有兩組對邊平行，既然平行，那我就想它兩個角能否組成和那個平行四邊形長度一樣的長方形呢？我測試了一下，發現可以，那這樣計算平行四邊形的面積就容易多了，下面就是我的研究方法。圖一：先畫出平行四邊形，再畫一條頂點上的高，沿高剪下一個三角形。圖二：把剪下的三角形再拼在另一個三角形旁邊，一個長方形就轉化成了。

韓振：大家看，平行四邊形變成長方形面積有沒有變化？

生：面積不變。

韓振：拼成的長方形的長等于平行四邊形的什么？長方形的寬等于平行四邊形的什么？

生：長方形的長等于平行四邊形的底，長方形的寬等于長方形的高。

韓振：因為長方形的面積=長×寬，那么平行四邊形的面積=底×高。

馬俊：大家對我們的介紹有什么疑問嗎？

張瑞林：非沿頂點剪下來嗎？

成員一：也可以沿別的地方剪下來。

師：你能演示給大家看嗎？

這位同學走到臺前給大家演示。

師：可是你還是沿頂點剪的呀，人家的問題是非沿頂點剪下來嗎？

聽了老師的疑問，學生猶豫了一下說：我認為不可以，因為從別的地方剪不可以和梯形拼成長方形。

張瑞林：可是我認為可以，我來給大家演示。說著便走到了臺前。

看到別組的成員要演示，組員三馬上說：我認為可以沿其它的地方剪下來，拼成長方形。邊說著邊演示給大家看

張瑞林：我就說嘛你為什么非說要沿頂點剪呢。

師：看來不僅可以沿頂點剪，只要怎樣剪就可拼成長方形？

生：只要沿平行線間的垂直往下剪就可以。

師：也就是沿什么剪？

曹原：也就是沿著平行四邊形的任意一條高剪就可以。

師：她概括得怎么樣？

生：非常好。

呂芃霖：那如果平行四邊形很細怎么辦？比如說只有1厘米寬。

張瑞林：很細也可以呀，比如說1毫米。

呂芃霖很疑惑的舉起了手。

師：你還有什么問題嗎？

呂芃霖：我還想證實我的想法。可是我認為這個圖形就不能沿這條高剪，他拿著一個又矮又長的平行四邊形走到臺前形想駁倒大家。如圖：

張瑞林：請問你畫的是高嗎？

呂芃霖：我認為是高。

師：同學們說呢?

眾生：他畫的不是高，根本就不垂直。

可是呂芃霖不相信自己畫的不是高，只好借用三角尺現場量給他看，張瑞林接著在附近畫了一條高，剪下來拼成了長方形，呂芃霖回到了座位，猶豫著接受了大家的意見。

我看出了他還是有點疑惑的，課堂又沒有太多的時間，只好說：“如有疑問，我們課下再研究。”

師：還有哪些同學來展示你們與眾不同的方法？

宋雨虹：我們發現，平行四邊形可以分成兩個相同的三角形，如圖：

三角形的面積公式=底×高÷2，平行四邊形的面積=兩個三角形的面積，所以平行四邊形的面積公式=底×高÷2×2=底×高，我們沒有學過三角形的面積，是怎么得到的呢？下面由陳平同學給大家解答。

陳平：我發現長方形、正方形都可以分成兩個相同的直角三角形。

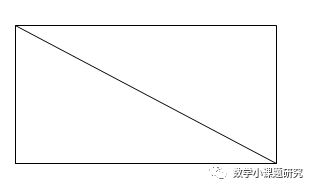
三角形的高=長方形的寬，三角形的底=長方形的長

長方形的面積=長×寬

三角形的面積=長×寬÷2

雨虹：大家還有什么疑問嗎？

生：你們研究的是直角三角形，那如果不是直角三角形怎么辦？

宋雨虹：我們小組的同學也提出過類似的問題。我們發現，無論銳角三角形和鈍角三角形，只要畫出他們的高，都可以分成兩個直角三角形，再把那兩個直角三角形的上方畫出兩個三角形，就拼成了長方形。如圖：

原來三角形的面積等于長方形面積的一半，這個長方形的面積等于底×高，因此，三角形的面積=底×高÷2。

師：平行四邊形轉換成三角形，三角形轉換成直角三角形，直角三角形轉換成長方形，就是在這不斷地地轉換中，讓我們找到了各種圖形之間的聯系，而且我們還有了意外的收獲，三角形的面積=底×高÷2。

呂芃霖：我還有一種方法證明三角形的面積=底×高÷2。可以找到三角形兩條斜邊的中點，做垂線段，沿垂線段剪下，拼到上方，變成長方形，如圖。

長方形的底是三角形底的一半，寬是三角形的高，長方形面積=長×寬，所以三角形面積=底÷2×高

生：我覺得你這種方法真是稀有的，你是怎么想出這種獨特的方法的？

呂芃霖：賀童是用兩個三角形研究的，我就想能不能用三角形自身來研究呢，就想出了這種方法。

生：你的這種研究精神值得我們學習。

生：既然出現了兩個求三角形的面積，肯定有一個是正確的吧？

生：我認為宋雨虹的方法對，因為她研究了多個三角形，而第二種只研究一個三角形。

生：我認為呂芃霖的方法對，他的方法適用于任意的三角形，第一種要找兩個相同的三角形。

生：我用底是10cm,高是6cm的三角形驗證，結果是一樣的！可以將這兩個公式概括為一個：三角形的面積=底×高÷2。

師：學了運算定律，大家就知道為什么都對了！有興趣的同學可以課下繼續研究。

師：孩子們，炎炎烈日，卻擋不住我們小課題研究的腳步，通過這幾日的研究和今天的交流，你有哪些收獲？

生：我們要用自己的方法和見解解決生活中的問題，還從別人的研究中學會許多好的方法。解決問題的方法是多種多樣的。

生：只要努力，沒有解決不了的問題，讓我們一起努力吧。

四、課后研究及成果展示交流

(一)課題：是不是沿平行四邊形的任意一條高剪都能拼成長方形

記起課堂上呂芃霖對沿平行四邊形的任意一條高剪都能拼成長方形問題的爭辯，及其他最后的猶豫，我想畫錯了高不應是他的本意，他是班上數學最好的同學，可能是我忽視了他的想法。課后馬上找到他，果然他說自己的本意是：假如是一個很長很細的平行四邊形，高畫在了外面怎么辦?那就繼續研究吧。當天結論就出來了：如果高畫在了圖形的外面，剪下來的部分是不能直接拼成平行四邊形的，所以課堂上我們說的“沿任意一條高剪下的圖形都能和梯形拼成平行四邊形”這句話是不嚴密的。如圖：

(二)課題：如果平行四邊形面積相等，底相等，周長會有什么變化？

研究人：徐悅鈞

為了研究這個問題，我畫了如下幾個圖形，它們的面積相等，底相等，但圖形1的周長是15厘米，圖形2的周長是15.4厘米，圖形3的周長積是16厘米，圖形4的周長是17.4厘米，我反復研究，得出的結論是：平行四邊形面積相等，底相等，斜邊越斜，周長越長，斜邊越直，周長越短。也就是相鄰的兩個夾角相差越小，周長越短，相鄰的兩個夾角相差越大，周長越長。

五、教學反思

1.每位學生都經歷了探究的過程

以小課題研究的方式進行學習，每位同學都經歷了觀察、猜想、思考、計算、實驗、推理、聯想、概括、爭辯、獲得共識的過程。在研究階段，有的學生用的時間長，幾天都找不到一點眉目；有的學生有的時間少，幾十分鐘就能有初步的想法，真實反映了學生之間的差距。面對多數同學認為平行四邊形的面積等于鄰邊乘鄰邊的慣性思維，教師給了學生充足的探究空間，讓他們自己暴露思維痕跡，自己糾正。這個過程是常規課堂40分鐘所不能給學生的。通過這樣的探究過程，學生找到了平行四邊形面積計算公式的來龍去脈，并獲得了選擇方法來驗證猜想、解決問題的基本經驗。通過這樣的方式，學生經歷了研究過程，能逐步養成獨立思考、善于質疑和自主探究的習慣，達到學習的理想境界。

2.每位學生展示了不一樣的精彩

在常規教學中，由于每節課只有40分鐘，我們很難看到每一位學生對問題的獨特見解，基本上是幾位學習尖子生展現自己的想法，大多數同學當觀眾與聽眾，跟著尖子生走。整堂課下來，雖學會了相關內容，卻往往不是自己思考、探究的成果。這些數學優秀的同學，展現的也并不完全是自己的思維，因為他們善于預習，會發現教材給我們提供的各種思路。而這些思路，很多時候是教材編者的思路，并不一定是孩子的思維方法。我們給了每個孩子真正的思考時間，便發現了每個人與眾不同的思維和方法。

3.每位學生在辯析中有所發展

在課前，每位學生都做了深入的研究，而且他們的研究方法各不相同，所以當他們在課堂上展現出來，出現了一幕幕精彩的質疑爭辯場景。面對別人的研究成果，孩子們不斷質疑，爭辯，討論，直至所有的結論得到所有同學的認可。在這樣的學習過程中，孩子們逐步養成全面考慮問題和善于從別人身上取長補短意識，達到共識、共享、共進的境界。

4.每位學生都提高了學習效率

經過幾天的時間，學生才推導出公式，有的學生甚至走了很多彎路，這樣的學習效率不是很低嗎？教師必須掌握學生研究進程，對他們的研究情況有所了解，并提供有針對性的幫助，這樣教不是很費力嗎？然而，通過幾天的研究，學生的能力卻得到切實的開發，更重要的是增強了學生的學習興趣，他們樂此不疲，各顯神通，累并快樂著。而且，學生不僅推導出平行四邊形的面積計算公式，對公式有了更深刻的理解，也推導出了三角形的面積計算公式，自然而然地探究了后面要學習的內容，建立起這些知識之間的縱橫聯系！隨著對平行四邊形面積計算公式的研究，三角形面積計算公式也一并解決了，可謂是提高了學習效率。更關鍵的是，學生獲得了“能夠帶走”的方法和經驗，這無疑會提高學生學習其他內容時的效率。對教師而言，學生自己能探究得到的，教師也就不用事必躬親，勞神費力了！這不也是一種解放嗎？而且是體現了教學藝術的解放！(作者系日照市慧通小學)

??本文已在《小學數學教師》發表。