機器學習原理與算法（六） 支持向量機

?版權聲明：本系列文章為博主原創文章，轉載請注明出處！謝謝！

---

?本章索引：

從第3章的Logistic回歸算法開始，我們一直在討論分類問題。在各種不同的分類算法中，...，我們一直在討論如何分類，而沒有考慮到分類的效果如何。假設不考慮分類算法本身的思想，運算復雜度等問題，是不是所有的分類效果都是一樣的呢？答案是否定的。本章將帶領大家一起討論這個問題，以及由此引出的一類非常重要的分類算法 -- 支持向量機。在錄制CS229的時候，吳老師不斷強調支持向量機在分類算法問題中的重要性，并認為它在各方面的表現都不比神經網絡遜色。不過目前在在人工智能領域貌似是神經網絡用的更多一些，不太確定是不是因為這些年神經網絡的發展更好，畢竟CS229已經錄完10多年了。在求解支持向量機問題的時候，可以使用核函數來提到計算的效率。本章將設計大量的最優化問題，如果最優化的基本問題遺忘的話，建議回去再看一遍番外篇。

1. 最優分類問題的討論

2. 最優間隔分類器

3. 支持向量機算法

4. 核函數

5. 正規化技術和不可分場景

6. SMO算法

---

?

1. 最優分類問題的討論?

在二分類算法中，我們最終的目的是找到一個超平面來劃分兩類數據。例如，待分類的樣本分布在二維空間，那么超平面就是一條直線；如果是三維空間，那么超平面就是一個平面；一般情況下，對于任意維的空間，我們把這個界限稱為超平面。直覺上，越靠近這個超平面的樣本點，我們認為它和另一類的距離越近，分類的確定性就越低；越遠離超平面的樣本點，它的分類確定性就越高。比如下面的圖：雖然A和C都屬于"X"類，但我們認為A屬于"X"類的確定性要大于C屬于"X"類的確定性。

?

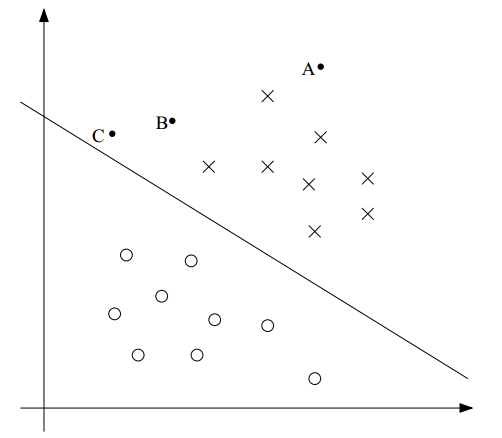
另一方面，如果分界超平面再向右上移動一些，那么有可能C就被分到"O"類中了。很明顯C距離"X"類更近一些，它更應當被分到"X"類。把C分到"O"類的超平面不是一個好的分界超平面。正如本章索引中提到的，我們的確需要關注分類算法的效果，使得分界超平面的位置能更好的區分兩類樣本。什么叫更好的分類的效果呢？之前也提到了，我們對A屬于"X"類非常確信，因為它更遠離分界超平面。因此，直覺上，如果一個分界超平面能盡可能的原理樣本點，那么它的分類效果就非常的好。

?

下面讓我們用數學語言來描述這一結論。

為了更好的表示支持向量機算法，我們需要對之前用在分類算法中的表達式做一些修改：

?(1) 我們用$y\in\{-1,1\}$來表示二分類算法中的標簽，代替了以前的$y\in\{0,1\}$。并用$y=1$表示上圖中的“X"類，用$y=-1$表示"O"類。

?(2) 我們丟棄$x_0=1$的假設和$\theta_0x_0+\theta_1x_1+\theta_2x_2 = \sum_{i=0}^n \theta_ix_i = \theta^Tx$的表示方法，改為$b+\theta_1x_1+\theta_2x_2 = b + \sum_{i=1}^n \theta_ix_i = w^T +b$的形式，其中$w=[\theta_1,\cdots,\theta_n]^T$。也就是說，我們現在把截距單獨的拿出來，表示為$b$，并用$w$代替之前的$\theta$。

因此，分類算法的假設$h_\theta(x)$表示為：

\begin{equation} h_{w,b}(x) = g(w^Tx+b) \end{equation}

其中，當$z\geq 0$時$g(z) = 1$；其他情況下 $g(z) = -1$。

?

下面介紹函數間隔和幾何間隔。這兩個概念是定量描述分類超平面效果好壞的標準，也不斷出現在本章后面的算法中。

對于訓練集合中的訓練樣本$(x^{(i)}, y^{(i)})$，定義$(w,b)$相對于它的函數間隔(Functional Margin)為：

\begin{equation*} \hat{\gamma}^{(i)} = y^{(i)}(w^Tx +b) \end{equation*}

在這個定義下有如下結論：

?(1)?如果$y^{(i)}(w^Tx+b) \ge 0$，那就表明我們對這個訓練樣本的預測是正確的。（對照上面的圖，在二維空間思考下，應該能想明白）

?(2) 如果$y^{(i)} = 1$，為了使函數間隔更大，我們應當讓(w^T+b)是一個較大的正數；反之，如果如果$y^{(i)} = -1$，為了使函數間隔更大，我們應當讓(w^T+b)是一個較大的負數。

結論(2)使得我們不好直接用函數間隔來衡量超平面的分類效果。我們上面講過，對于$g(z)$，當$z\geq 0$時$g(z) = 1$；其他情況下 $g(z) = -1$。只有$z$的正負會影響$g$的取值，因此，我們完全可以任意縮放$(w,b)$而不影響$g$和$h_\theta(x)$的取值，因為$g(w^Tx+b) = g(2w^Tx+2b)$，結果就是我們總可以取到無限大的函數間隔。

這是針對一個訓練樣本的函數間隔的定義。針對整個訓練集合，我們定義函數間隔為；

\begin{equation*} \hat{\gamma} = \mathop{min}\limits_{i=1,\cdots,m}\hat{\gamma}^{(i)} \end{equation*}

對于訓練集合中的訓練樣本$(x^{(i)}, y^{(i)})$，定義$(w,b)$相對于它的幾何間隔(Geometric Margin)為：

\begin{equation*}
\gamma^{(i)} = y^{(i)}((\frac{w}{\Vert w \Vert})^T x^{(i)} + \frac{b}{\Vert w \Vert})
\end{equation*}

我們借助下圖來解釋它的意義：

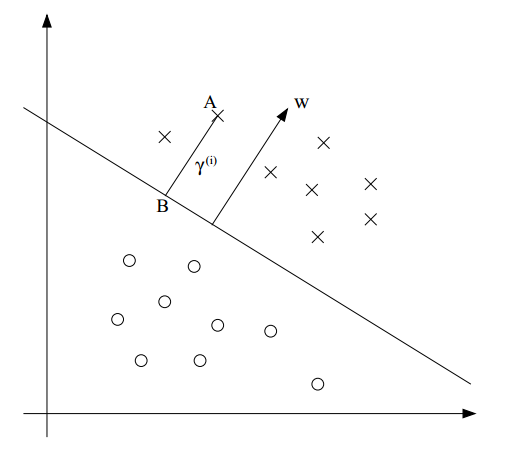
假設我們想計算樣本點A $(x^{(i)}, y^{(i)}$到超平面的幾何距離$\gamma^{(i)}$，也就是線段AB。圖中的分類超平面其實就是$w^Tx+b=0$，這個超平面的法向量是$w$，單位法向量是$w/\Vert w \Vert$。由于點A代表$x^{(i)}$，因此B為: $x^{(i)} - \gamma^{(i)} \cdot w/\Vert w \Vert$。同時，B也在超平面$(w^Tx+b)$上，故帶入，有

\begin{equation*}
w^T(x^{(i)} - \gamma^{(i)} \frac{w}{\Vert w \Vert}) + b =0
\end{equation*}

解出$\gamma^{(i)}$，就可得到：

\begin{equation*}
\gamma^{(i)} = (\frac{w}{\Vert w \Vert})^T x^{(i)} + \frac{b}{\Vert w \Vert}
\end{equation*}

上面只是考慮了$y=1$的情況，如果推廣到一般情況，那么就得到了上面幾何間隔的定義：

\begin{equation*}
\gamma^{(i)} = y^{(i)}((\frac{w}{\Vert w \Vert})^T x^{(i)} + \frac{b}{\Vert w \Vert})
\end{equation*}

從幾何間隔的定義可以得到幾何間隔的重要性質：我們可以任意縮放$w$和$b$，而不改變幾何間隔。

觀察下函數間隔和幾何間隔之間的關系，很明顯，如果$\Vert w \Vert = 1$，那么幾何間隔就等于函數間隔。

最后，把幾何間隔的定義推廣到整個訓練集合的幾何間隔，類似于有函數間隔，我們有：

\begin{equation*} \gamma = \mathop{min}\limits_{i=1,\cdots,m} \gamma^{(i)} \end{equation*}

?

總結：上面的討論告訴我們，分類算法不僅要保證分類的正確性，還要進一步保證對于分類結果的確定程度。我們定義了函數間隔和幾何間隔來定量描述分類的確定程度。

?

2. 最優間隔分類器

在上節的討論中了解到，為了得到最好的分類效果，我們應當尋找一個幾何間隔盡可能大的判決邊界。用最優化的思想來描述這種需求。

假設訓練集合是線性可分的，那么上面的需求等價于下面的最優化問題：

\begin{equation*}
max_{\gamma,w,b}\ \ \gamma
\end{equation*}

\begin{equation*}
s.t.\ \ y^{(i)}(w^T x^{(i)} + b) \geq \gamma, \ i=1,\cdots,m
\end{equation*}

\begin{equation*}
\Vert w \Vert =1
\end{equation*}

目標函數的目的是最大化$\gamma$，使得訓練集合中所有訓練樣本的函數間隔都大于$\gamma$，且$\Vert w \Vert =1$。約束$\Vert w \Vert =1$的目的是使得函數間隔等于集合間隔。如果能求解這個最優化問題，那么最優間隔分類器的就得到了。

事與愿違，問題中的等式約束條件$\Vert w \Vert =1$是一個非常討厭的非凸約束，我們無法對問題進行有效的求解。因此，我們改寫上述問題：

\begin{equation*}
max_{\gamma,w,b}\ \ \frac{\hat{\gamma}}{\Vert w \Vert}
\end{equation*}

\begin{equation*}
s.t.\ \ y^{(i)}(w^T x^{(i)} + b) \geq \hat{\gamma}, \ i=1,\cdots,m
\end{equation*}

這里，我們改為優化$\frac{\hat{\gamma}}{\Vert w \Vert}$。這個問題和上一個問題是等價的，只是擺脫了$\Vert w \Vert =1$這個非凸約束。然而，目標函數$max_{\gamma,w,b}\ \ \frac{\hat{\gamma}}{\Vert w \Vert}$仍然是一個非凸函數，因此這也不是一個凸優化問題（可曾記得，凸優化問題要求目標函數和約束條件都是凸函數？）。

既然還是不行，那我們再進一步。記得之前的結論吧，我們可以任意縮進$w$和$b$，這并不會改變幾何間隔的大小。那就開干，在上面優化問題的基礎上，我們縮進$w$和$b$，直到函數間隔$\hat{\gamma}=1$。現在好了，本來待優化的目標函數是$\frac{\hat{\gamma}}{\Vert w \Vert}$，現在分子被我們縮進成了1，我們優化的目標就變成了最大化$\frac{1}{\Vert w \Vert}$。等價的，我們可以轉化為下列優化問題：

\begin{equation*}
min_{\gamma,w,b}\ \ \frac{1}{2}{\Vert w \Vert}^2
\end{equation*}

\begin{equation*}
s.t.\ \ y^{(i)}(w^T x^{(i)} + b) \geq 1, \ i=1,\cdots,m
\end{equation*}

這下，目標函數和約束條件都是凸函數了，可以用很多軟件直接進行無定制化的求解。

?

3.支持向量機算法

到這里，最優間隔分類器的問題應該是已經結束了，我們還要繼續做什么呢？我們能做的，就是繼續為算法尋找更高效的求解方法。繼續前進需要了解拉格朗日乘數法，這是一種凸優化問題的求解方法，我把它貼在這里。請確保你完全看明白了再繼續。

回到我們的上節最后的優化問題：

\begin{equation*}
min_{\gamma,w,b}\ \ \frac{1}{2}{\Vert w \Vert}^2
\end{equation*}

\begin{equation*}
s.t.\ \ y^{(i)}(w^T x^{(i)} + b) \geq 1, \ i=1,\cdots,m
\end{equation*}

把約束條件寫成函數$g_i(w)$，即

\begin{equation*} g_i(w) = -y^{(i)}(w^T x^{(i)} +b) +1 \leq 0 \end{equation*}

根據KKT對偶補充條件，只有使得$g_i(w)=0$的樣本點，才能有$\alpha_i \ge 0$。$g_i(w)=0$意味著函數間隔$-y^{(i)}(w^T x^{(i)} +b)$取到了最小值1，如下圖虛線上的三個點(兩個"X"和一個"O")。只有這三個訓練樣本對應的的$\alpha_i$是非0的。這三個點就稱為支持向量。一般來講，支持向量的數量是很少的。

正如我們在介紹拉格朗日乘數法的對偶形式時用的內積一樣，現在讓我們把我們的算法也寫成內積的形式，這對我們后面的核函數來說是很重要的一步。

構建拉格朗日算子如下：

\begin{equation*}
\mathcal{L} (w,b,\alpha) = \frac{1}{2} {\Vert w \Vert}^2 - \sum_{i=1}^m \alpha[y^{(i)}(w^T x^{(i)} + b) - 1]
\end{equation*}

讓我們來找到上述問題的對偶形式。為了得到對偶形式，我們需要先找到合適的$w$和$b$，使得$\mathcal{L} (w,b,\alpha) $最小化，并得到$\theta_D$。

對$w$和$b$求偏導即可，然后讓偏導數等于零即可：

\begin{equation*}
\nabla \mathcal{L} (w,b,\alpha) = w - \sum_{i=1}^m \alpha_i y^{(i)} x^{(i)} = 0
\end{equation*}

求解，得到：

\begin{equation*}
w= \sum_{i=1}^m \alpha_i y^{(i)} x^{(i)}
\end{equation*}

我們把w帶入拉格朗日乘數，然后化簡，得到：

\begin{equation*}
\mathcal{L} (w,b,\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j (x^{(i)})^T x^{(j)} - b\sum_{i=1}^m \alpha_i y^{(i)}
\end{equation*}

然后再對$b$求偏導：

\begin{equation*}
\frac{\partial}{\partial b} \mathcal{L} (w,b,\alpha) = \sum_{i=1}^m \alpha_i y^{(i)} = 0
\end{equation*}

對比上一個式子，它的最后一項就是0。所以得到以下結果：

\begin{equation*}
\mathcal{L} (w,b,\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j (x^{(i)})^T x^{(j)}?
\end{equation*}

然后，我們把$\alpha_i \geq 0$和對$b$的偏導的結果放在一起，就有下面的對偶優化問題：

\begin{equation*}
max_\alpha \ \ W(\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle
\end{equation*}

\begin{equation*}
s.t.\ \ \alpha_i \geq 0, \ i=1,\cdots,m
\end{equation*}

\begin{equation*}
\sum_{i=1}^m \alpha_i y^{(i)} = 0
\end{equation*}

我們可以解決這個對偶問題，就等于解決了原問題。在上面這個優化問題中，待優化的參數是$\alpha$，如果我們可以直接求出$\alpha$，那么我們可以用公式9去找到最優的$w$(作為$\alpha$的函數)，然后再用原問題最優的b：

\begin{eqnarray*}
w^T x +b & = & (\sum_{i=1}^m \alpha_i y^{(i)} x^{(i)}) ^T x + b \\
& = & \sum_{i=1}^m \alpha_i y^{(i)} \langle x^{(i)} ,x \rangle + b
\end{eqnarray*}

觀察一下公式(9)，我們發現，$w$的值之和$\alpha$有關。如果已經根據訓練集合建立了模型，那么當我們有新的樣本$x$需要預測時，我們要計算$w^T x +b $，然后如果結果大于0，就斷定$y=1$：

\begin{eqnarray*}
w^T x +b & = & (\sum_{i=1}^m \alpha_i y^{(i)} x^{(i)}) ^T x + b \\
& = & \sum_{i=1}^m \alpha_i y^{(i)} \langle x^{(i)} ,x \rangle + b
\end{eqnarray*}

因此，如果我們能得到$\alpha$，那么我們只需要計算$x$和訓練集合中的其他樣本的內積即可。另外，之前也提到了，除了少量的支持向量，其他的$\alpha$都是0，因此，我們只需要計算$x$和支持向量之間的內積。

總結：我們深入研究原問題的對偶問題，得到了很多有用的結論。最重要的是，我們最終把問題轉化成了特征向量之間的內積形式。這就是支持向量機算法。在下一部分，我們介紹核函數，它可以幫助我們高效的解決支持向量機算法，并且可以求解高維甚至無限維問題。

?

4. 核函數

回想我們在線性回歸課程中的一個例子，我們用住房面積$x$估計房屋價格的時候，曾經用二次曲線$y=\theta_0+\theta_1x+\theta_2x^2$來做擬合。本來只有一個輸入變量$x$的問題轉化成了多個，這里是兩個。某些場景下，我們需要做這種輸入特征的映射，比如訓練集合用三次方曲線建模時更好，我們就定義這樣的映射為$\phi$，$\phi:\? \mathbb{R} \mapsto mathbb{R}^3 $：

\begin{equation*} \phi(x) = \begin{bmatrix} x \\ x^2 \\ x^3 \end{bmatrix} \end{equation*}

在這里，如果我們把回歸問題改成分類問題，例如根據房屋面積判斷房屋在六個月內是否能賣出去，那么我們可以用支持向量機算法來計算。之前我們討論的支持向量機算法中，輸入變量都是標量$x$，現在都替換成了三維向量$\phi(x)$，之前支持向量機算法中的內積$\langle x,z \rangle$也要替換成$\langle \phi(x), \phi(z) \rangle$。一般來講，給定一個映射$\phi$，我們定義相應的核函數為$K(x,z) = \phi(x)^T \phi(x)$。因此，所有內積$\langle x,z \rangle$都可以替換成核函數$K(x,z)$。

此時，給定$\phi$，我們可以很容易的得到$\phi(x)$和$\phi(z)$，然后求內積從而計算出$K(x,z)$。神奇的是，有時候計算$K(x,z)$是很容易的，反而計算$\phi(x)$是很難的，比如映射的維數很高的時候。在這種情況下，我們可以用核函數$K(x,z)$很容易的計算出高維空間的支持向量機，而不用去計算映射$\phi(x)$。

來看一個具體的例子，假設$x, z \in \mathbb{R}^n$，核函數為$K(x,z)$ =(x^Tz)^2,即

\begin{eqnarray*}
K(x,z) & = & (\sum_{i=1}^n x_i z_i)(\sum_{j=1}^n x_j z_j) \\
& = & (\sum_{i=1}^n \sum_{j=1}^n x_i x_j z_i z_j \\
& = & (\sum_{i,j=1}^n (x_i x_j) (z_i z_j) \\
& = & \langle (\phi(x))^T,(\phi(x)) \rangle
\end{eqnarray*}

?因此，$K(x,z)=\phi(x)^T \phi(z)$，其中，$n=3$時的映射$\phi$是：

?\begin{equation*} \phi(x) = \begin{bmatrix} x_1 x_1 \\ x_1 x_2 \\ x_1 x_3 \\ x_2 x_1 \\ x_2 x_2 \\ x_2 x_3 \\ x_3 x_1 \\ x_3 x_2 \\ x_3 x_3 \end{bmatrix} \end{equation*}

我們注意到，計算高維的$\phi(x)$需要$O(n^2)$的時間復雜度，但是計算$K(x,z)$只需要$O(n)$的時間復雜度。

再來看另一個相關的核函數：

\begin{eqnarray*}
K(x,z) & = & (x^T z + c)^2 \\
& = & \sum_{i,j=1}^n(x_i x_j) (z_i z_j) + \sum_{i=1}^n (\sqrt{2c}x_i) (\sqrt{2c} z_i) + c^2
\end{eqnarray*}

$n=3$時的映射是：

\begin{equation*} \phi(x) = \begin{bmatrix} x_1 x_1 \\ x_1 x_2 \\ x_1 x_3 \\ x_2 x_1 \\ x_2 x_2 \\ x_2 x_3 \\ x_3 x_1 \\ x_3 x_2 \\ x_3 x_3 \\ \sqrt{2c}x_1 \\ \sqrt{2c}x_2 \\ \sqrt{2c}x_3 \\ c \end{bmatrix} \end{equation*}

這樣可以用參數$c$控制著$x_i$和$x_i x_j$之間的相對權重。

一般來講，核函數$K(x,z) = (x^T z + c)^d對應著$ \begin{pmatrix} n+d \\ d \end{pmatrix}$維的映射，計算它的時間復雜度是$O(n^d)$，而計算核函數$K(x,z)$的時間復雜度卻仍然是$O(n)$，且完全不涉及高維向量的計算。

?

下面來討論核函數的選擇相關的直覺（不一定完全正確）。如果$\phi(x)$和$\phi(z)$是足夠相近的，那么$K(x,z)=\phi(x)^T \phi(z)$的值應該很大。反之，如果$\phi(x)$和$\phi(z)$不相近，類似于正交關系，那么$K(x,z)=\phi(x)^T \phi(z)$應該接近于0。所以，我們可以認為$K(x,z)$是$\phi(x)$和$\phi(z)$相似程度的大致估計。

我們可以根據上述直覺提出一些靠譜的核函數：

\begin{equation*} K(x,z)=exp(\ \frac{{\Vert x-z \Vert}^2}{2\sigma^2}) \end{equation*}

很容易看出來，如果$x$和$z$比較接近的話，它的值為1；反之，則值為0。這個核函數叫高斯核函數，它對應的映射$\phi$是無限維的。

?

如何判斷是一個核函數是合法的呢？

假設$K$的確是一個合法的核函數，它對應的映射是$\phi$。對于訓練集合$\{ x^{(1)},\cdots, x^{(m)} \}$,定義一個$m \times m$的矩陣K，它的第$(i,j)$個元素的值$K_{i,j} = K(x^{(i)}, x^{(j)} )$。這個矩陣K稱為核矩陣（表示方法有點混亂，都是用K表示，但一個是函數，一個是矩陣）。

根據假設，$K$是一個合法核函數，那么必有?$K_{ij} = K(x^{(i)}, x^{(j)}) = \phi(x^{(i)})^T \phi(x^{(j)}) = \phi(x^{(j)})^T \phi(x^{(i)}) = K(x^{(j)}, x^{(i)}) = K_{ji}$，即$K$是一個對稱矩陣。

用$\phi_k(x)$表示向量$\phi(x)$的第$k$個坐標，對于任意向量$z$，都有：

\begin{eqnarray*}
z^T K z & = & \sum_i \sum_j z_i K_{ij} z_j \\
& = & \sum_i \sum_j z_i \phi(x^{(i)})^T \phi(x^{(j)}) z_j \\
& = & \sum_i \sum_j z_i \sum_k \phi_k(x^{(i)}) \phi_k(x^{(j)}) z_j \\
& = & \sum_k \sum_i \sum_j z_i \phi_k(x^{(i)}) \phi_k(x^{(j)}) z_j \\
& = & \sum_k (\sum_i z_i \phi_k(x^{(i)}))^2 \\
\geq 0
\end{eqnarray*}

也就是說，對于任意的$z$，都有$K \geq 0$。總結成以下結論：

Mercer定理：給定$K: \mathbb{R}^n \times \mathbb{R}^n \mapsto \mathbb{R}$. K是合法核函數的充要條件是對于任意的$\{ x^{(1)},\cdots, x^{(m)} \}, (m \le \infty)$，對應的核矩陣是對稱半正定的。

?

5. 正則化和線性不可分

直到現在，在我們的假設中，訓練集合都是線性可分的。支持向量機算法可以把特征映射到高維，將一些線性不可分的問題轉換為線性可分的問題，但我們很難保證總是這樣。此外，某些情況下，我們也不希望找出精確的分界平面，例如，下圖中的左圖展示了一個最優間隔分類器；但當訓練集合中混入了一些離群點時，我們找到的最優間隔分類器其實很糟糕，它與樣本點之間的間隔很小。

?

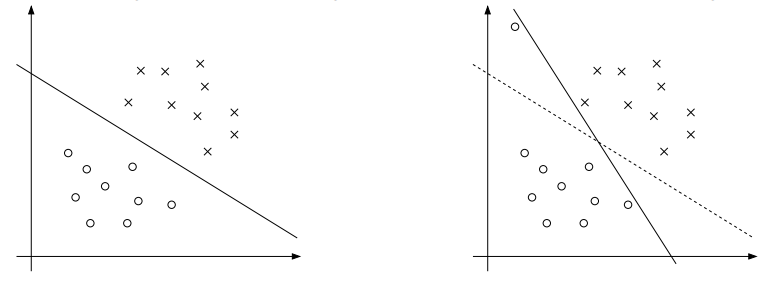
為了解決這類線性不可分問題，我們重構了算法：

\begin{equation*}
min_{\gamma,w,b} \ \ \frac{1}{2} {\Vert w \Vert}^2 + C \sum_{i=1}^m \xi_i
\end{equation*}

\begin{equation*}
s.t. \ \ y^{(i)}(w^T x^{(i)} + b ) \geq 1-\xi_i, \ i=1,\cdots,m
\end{equation*}

\begin{equation*}
\xi_i \geq 0,\ i=1,\cdots,m
\end{equation*}

在函數間隔相關的約束條件上增加了一個懲罰量$\xi_i$ ($L1$正則化)，使得函數間隔有可能小于1了（回想，原版的支持向量機算法中，函數間隔最小只能等于1）。并且，如果懲罰項$\xi_i \ge 1$，函數間隔可能是負數。我們之前提過，如果函數間隔$y^{(i)}(w^T x^{(i)} + b ) \ge 0$則表示分類正確。可能出現小于0的函數間隔也就意味著，我們允許分類錯誤的樣本點出現，這可以很好的應對上圖中的情形。

這是一個凸優化問題，我們用之前講過的對偶問題的方式來求解。寫出拉格朗日算子：

\begin{equation*}
\mathcal{L} (w,b,\xi,\alpha,\gamma) = \frac{1}{2}w^Tw + C\sum_{i=1}^m \xi_i - \sum_{i=1}^m \alpha_i [y^{(i)} (x^Tw+b)-1 + \xi_i] - \sum_{i=1}^m r_i \xi_i
\end{equation*}

推導出它的對偶形式：

\begin{equation*}
max_\alpha W(\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle
\end{equation*}

\begin{equation*}
s.t. \ \ 0 \leq \alpha_i \leq C, \ i=1,\cdots,m
\end{equation*}

\begin{equation*}
\sum_{i=1}^m \alpha_i y^{(i)} = 0
\end{equation*}

注意到，在做了$L1$正則化以后，對偶問題唯一的改變就是約束條件從$0 \leq \alpha$變成了 $0 \leq \alpha \leq C$。KKT對偶補充條件是：

\begin{equation*}
\alpha_i = 0 \Rightarrow y^{(i)} (w^T x^{(i)} + b) \geq 1
\end{equation*}

\begin{equation*}
\alpha_i = C \Rightarrow y^{(i)} (w^T x^{(i)} + b) \leq 1
\end{equation*}

\begin{equation*}
0 \le \alpha_i \le C \Rightarrow y^{(i)} (w^T x^{(i)} + b) = 1
\end{equation*}

?

6. 順序最小優化算法

先介紹坐標上升法：

假設我們要優化一個無約束問題：

\begin{equation*}
\max_\alpha W(\alpha_i, \alpha_2, \cdots, \alpha_m)
\end{equation*}

方法是描述如下：

Loop until convergence: {

? ? For $i=1,\cdots,m,${

? ? ? ? $alpha_i := argmax_{\hat{alpha}_i}\ W(\alpha_i,\cdots,\alpha_{i-1}, \hat{\alpha}_i, \alpha_{i+1},\cdots, \alpha_m)$

? ? }

}

解釋：每次迭代，坐標上升法保持所有$\alpha$固定，除了$\alpha_i$。然后相對于這個參數使函數取最大值。結合下面的圖再直觀的理解一下：

假設只有兩個$\alpha$，用橫坐標表示$\alpha_1$，縱坐標表示$\alpha_2$，因為每次迭代都是只改變一個$\alpha$，故優化的軌跡方向都是與坐標軸平行的。

?

回到上節的優化問題，讓我們來用坐標上升法計算：

\begin{equation*}
max_\alpha W(\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle
\end{equation*}

\begin{equation*}
s.t. \ \ 0 \leq \alpha_i \leq C, \ i=1,\cdots,m
\end{equation*}

\begin{equation*}
\sum_{i=1}^m \alpha_i y^{(i)} = 0
\end{equation*}

注意約束 $\sum_{i=1}^m \alpha_i y^{(i)} = 0$，如果我們直接應用坐標上升法，固定所有的$\alpha$除了$\alpha_i$，只改變$\alpha_i$，那么... 我豈不是連$\alpha_i$都不能改變了？怎么優化啊？所以，要對初始的算法做一些調整，每次改變兩個$\alpha$值。這個算法就稱為序列最小優化算法(Sequential Minimal Optimizaiton, SMO)，最小的意思是我們希望每次該表最小數目的$\alpha$。這個算法的效率非常高，與牛頓法比較的話，它收斂所需的迭代次數會比較多，但每次迭代的計算代價通常比較小。

Repeat till convergence {
1. Select some pair $\alpha_i$ and $\alpha_j$ to update next (using a heuristic that?tries to pick the two that will allow us to make the biggest progress?towards the global maximum).
2. Reoptimize $W(\alpha)$ with respect to $\alpha_i$ and $\alpha_j$, while holding all the?other $\alpha_k’s (k \neq i, j) fixed.
}

我們只要一直運行算法，直到滿足上一節的收斂條件即可。問題是，算法的第2步要求優化$W$，我們應該怎樣做呢？下面以$\alpha_1$和$\alpha2$為例來講解這個過程。

根據約束條件，有

\begin{equation*} \alpha_1 y^{(1)} + \alpha_2 y^{(2)} = -\sum{i=3}^m \alpha_i y^{(i)} \end{equation*}

由于等式右邊是固定的，我們就簡單的把它記為一個常數$\zeta$，即

\begin{equation*}\alpha_1 y^{(1)} + \alpha_2 y^{(2)} = \zeta?\end{equation*}

這是一個約束。還一個約束是

\begin{equation*}
0 \le \alpha_i \le C
\end{equation*}

把可選區域畫成圖，如下：

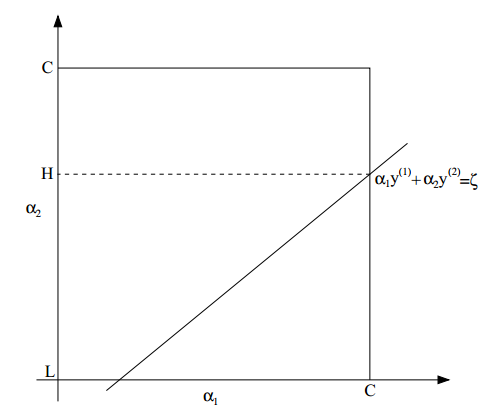
從圖中可以看出，$\alpha_2$的取值范圍是$[L, H]$，否則，$(\alpha_1, alpha_2)不可能同時滿足上面兩個約束$。

根據公式$ \alpha_1 y^{(1)} + \alpha_2 y^{(2)} = \zeta?$，我們可以把$\alpha_1$寫成$\alpha_2$的函數：

\begin{equation*} \alpha_1 = ( \zeta - \alpha_2 y^{(2)}) y^{(1)}. \end{equation*}

然后，有$W(\alpha_1, \alpha_2, \cdots, \alpha_m) = W((\zeta - \alpha_2 y^{(2)}) y^{(1)}, \alpha_2, \cdots, \alpha_m) $。把$\alpha_3,\cdots, \alpha_m$看做常數，可以看出這只是$\alpha_2$的二次函數。如果沒有取值范圍$[L, H]$的限制的話，只要求導數然后讓它為0即可，定義得到的值為$\alpha_2^{new, unclipped}$。再結合取值范圍$[L, H]$的限制，最終的優化結果為：

$$ \alpha_2^{new}=\left\{
\begin{array}{rcl}
H & & {\alpha_2^{new, unclipped} \ge H}\\
\alpha_2^{new, unclipped} & & {L \leq \alpha_2^{new, unclipped} \leq H} \\
L & & {\alpha_2^{new, unclipped} \le L}
\end{array} \right. $$

?