清北學堂Day4

?

（1）第一題

財富(treasure)

Time Limit:1000ms?? Memory Limit:128MB

題目描述

LYK有n個小伙伴。每個小伙伴有一個身高hi。

這個游戲是這樣的，LYK生活的環境是以身高為美的環境，因此在這里的每個人都羨慕比自己身高高的人，而每個人都有一個屬性ai表示它對身高的羨慕值。

這n個小伙伴站成一列，我們用hi來表示它的身高，用ai來表示它的財富。

每個人向它的兩邊望去，在左邊找到一個最近的比自己高的人，然后將ai朵玫瑰給那個人，在右邊也找到一個最近的比自己高的人，再將ai朵玫瑰給那個人。當然如果沒有比自己身高高的人就不需要贈送別人玫瑰了。也就是說一個人會給0,1,2個人玫瑰（這取決于兩邊是否有比自己高的人）。

每個人都會得到若干朵玫瑰（可能是0朵），LYK想知道得了最多的玫瑰的那個人得了多少玫瑰。(然后嫁給他>3<)

輸入格式(treasure.in)

??? 第一行一個數n表示有n個人。

??? 接下來n行，每行兩個數hi,ai。

輸出格式(treasure.out)

??? 一個數表示答案。

輸入樣例

3

4 7

3 5

6 10

輸出樣例

12

樣例解釋

第一個人會收到5朵玫瑰，第二個沒人送他玫瑰，第三個人會收到12朵玫瑰。

數據范圍

對于50%的數據n<=1000,hi<=1000000000。

對于另外20%的數據n<=50000，hi<=10。

對于100%的數據1<=n<=50000,1<=hi<=1000000000。1<=ai<=10000。

這道題從某種程度上來說是道一眼題。因為一眼就能看出O(n^2)的做法。但作為一個有追求的人，我還是認真的思考了一下有沒有O(n)的辦法，畢竟O(n^2)估計不能A。但后來也沒想出來，所以就……嗯。

我的代碼（沒想到竟然拿滿了，大概是數據有點弱）：

#include <iostream>
#include <cmath>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;
long long a[50101],h[50101];
long long sum[50101];
int main()
{
    
    freopen("treasure.in","r",stdin);
    freopen("treasure.out","w",stdout);
    
    int n;
    scanf("%d",&n);
    long long minn=1000000005,maxn=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%lld%lld",&h[i],&a[i]);
        minn=min(minn,h[i]);
        maxn=max(maxn,h[i]);
    }
    for(int i=1;i<=n;i++)
    {
        if(a[i]==maxn) continue;
        if(a[i]==minn) {sum[i-1]+=a[i];sum[i+1]+=a[i];continue;}
        for(int j=i-1;j>0;j--)
        {
            if(h[j]>h[i]) {sum[j]+=a[i];break;}
        }
        for(int j=i+1;j<=n;j++)
        {
            if(h[j]>h[i]) {sum[j]+=a[i];break;}
        }
    }
    long long ans=0;
    for(int i=1;i<=n;i++) ans=max(ans,sum[i]);
    printf("%lld",ans);
    //system("pause");
    return 0;
}

后來老師講了O(n)的做法。然而好像有點沒聽懂……代碼如下 ： ?@周老師

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
int n,s[50002],d[50002],ans[50002],ANS,a[50002],b[50002],r,i;
//b[i]表示第i個人收到的玫瑰數
//s[]單調隊列 
//d[i]在單調的數列中第i個位置是n個人中的哪個人 
int main()
{
    freopen("treasure.in","r",stdin);
    freopen("treasure.out","w",stdout);
    cin>>n;
    for (i=1; i<=n; i++) scanf("%d%d",&a[i],&b[i]);
    s[1]=a[1]; d[1]=1; r=1;
    for (i=2; i<=n; i++)
    {
        while (r!=0 && a[i]>s[r]) {ans[i]+=b[d[r]]; r--; }  
        r++;  //隊列中元素+1 
        s[r]=a[i];//推入單調隊列 
        d[r]=i;
    }
    s[1]=a[n]; d[1]=n; r=1;
    for (i=n-1; i>=1; i--)
    {
        while (r!=0 && a[i]>s[r]) { ans[i]+=b[d[r]]; r--; }
        r++;
        s[r]=a[i];
        d[r]=i;
    }
    for (i=1; i<=n; i++) ANS=max(ANS,ans[i]);
    cout<<ANS;
    return 0;
}

（2）第二題

正方形(square)

Time Limit:1000ms?? Memory Limit:128MB

題目描述

在一個10000*10000的二維平面上，有n顆糖果。

LYK喜歡吃糖果！并且它給自己立了規定，一定要吃其中的至少C顆糖果！

事與愿違，LYK只被允許圈出一個正方形，它只能吃在正方形里面的糖果。并且它需要支付正方形邊長的價錢。

LYK為了滿足自己的求食欲，它不得不花錢來圈一個正方形，但它想花的錢盡可能少，你能幫幫它嗎？

輸入格式(square.in)

??? 第一行兩個數C和n。

??? 接下來n行，每行兩個數xi,yi表示糖果的坐標。

輸出格式(square.out)

??? 一個數表示答案。

輸入樣例

3 4

1 2

2 1

4 1

5 2

輸出樣例

4

樣例解釋

選擇左上角在(1,1)，右下角在(4,4)的正方形，邊長為4。

數據范圍

對于30%的數據n<=10。

對于50%的數據n<=50。

對于80%的數據n<=300。

對于100%的數據n<=1000。1<=xi,yi<=10000。

我就是兩兩的枚舉端點，然后用這兩個端點擴出一個最小的正方形，之后搜一遍里面有多少點。如果點數夠了，就與當前的ans比較，保留小的。但是只過了兩個點，其他的都結果錯誤。可能是因為我默認正方形的左上角（或右上角）有一顆糖框住，但其實不一定。

我的代碼：

#include <iostream>
#include <cmath>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;
int n,C;
int xz,yz,xy,yy;
int maxn;
struct point
{
    int x,y;
    bool operator <(const point&o)const
    {
        if(x<o.x) return true;
        else if(x==o.x && y<o.y) return true;
        else return false;
    }
}a[1010];
void make_square(int i,int j)
{
    maxn=0;
    maxn=max(abs(a[j].y-a[i].y)+1,abs(a[j].x-a[i].x)+1);
    //cout<<maxn<<endl;
    if(a[i].y<=a[j].y) {xz=a[i].x;yz=a[i].y;xy=xz+maxn-1;yy=yz+maxn-1;}
    else
    {
        xz=a[i].x;yz=a[i].y-maxn+1;
        xy=a[i].x+maxn-1;yy=a[i].y;
    }
}
bool check()
{
    int cnt=0;
    for(int i=1;i<=n;i++)
    {
        if(a[i].x>=xz && a[i].x<=xy && a[i].y>=yz && a[i].y<=yy) cnt++;
        if(cnt>=C) break;
    }
    if(cnt>=C) return true;
    else return false;
}

int main()
{
    freopen("square.in","r",stdin);
    freopen("square.out","w",stdout);
    scanf("%d%d",&C,&n);
    for(int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y);
    sort(a+1,a+n+1);
    //for(int i=1;i<=n;i++) cout<<a[i].x<<" "<<a[i].y<<endl;
    int ans=10005;
    for(int i=1;i<n;i++)
    {
        for(int j=i+1;j<=n;j++)
        {
            make_square(i,j);
            if(check()) ans=min(ans,maxn);
        }
    }
    printf("%d",ans);
    //system("pause");
    return 0;
}

正解思路：

1.正方形的上、下、左、右一定有和糖果貼在一起的。不然會浪費。

因此我們可以枚舉上下左，之后找一個合適的右邊。最后再把這個長方形擴成正方形。

------------------------------插播：離散化---------------------------

Struct node{int x,y;}t[10005];
In cmp(node I,node j) {i.y<j.y;}

For(int i=1;i<=n;i++) cin>>a[i];
For(int i=1;i<=n;i++) t[i].x=I,t[i].y=a[i];
Sort(t+1,t+n+1,cmp);
For(int i=1;i<=n;i++)
{
If(t[i].y!=t[i-1].y) now++;
P[now]=a[t[i],x];
A[t[i].x]=now;
}

【例子】：

離散前：3 3 1 5

離散后：2 2 1 3

由此可見，離散化的作用是縮小空間。正好適用于這道題（由原來的10000*10000變為n*n的大小，二維空間大大縮小）

--------------------------------插播結束--------------------------------

算法改進：枚舉上邊和下邊。左邊為1的情況下，右邊是什么隨著左邊向右移動，右邊也一定向右移動。

左邊至多移動n次，右邊也至多移動n次，總共2n次

O（n^3）

繼續改進：

我們發現，本題答案是連續的。即，如果邊長為x可行，邊長為x+1也可行（至少覆蓋C個糖果）；假如x不可行，x-1也不可行。

由此可知，我們可以二分答案。

L,r判斷mid是否可行 --->正常的二分

之后，

枚舉上邊在哪里，下邊的位置是固定的。哪些糖果被夾在這段區間中? O(n)

再之后

左邊為1的情況下，右邊是什么

隨著左邊向右移動，右邊也一定向右移動。

左邊至多移動n次，右邊也至多移動n次，總共2n次?? O(n)

?

P.s:也可以用前綴和來做

標程：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
struct node {int x,y;} a[1005];
int C,n,L,R,mid,b[1005],o,i;
int cmp(node i,node j) {return i.x<j.x;}
int CMP(int i,int j) {return i<j;}
bool WORK(int l,int r)
{
     if (r-l+1<C) return false; o=0;
     for (int i=l; i<=r; i++) b[++o]=a[i].y;
     sort(b+1,b+o+1,CMP);
     for (int i=C; i<=o; i++)
       if (b[i]-b[i-C+1]<=mid) return true;
      return false;
}
bool OK(int x)
{
    int l=1;
    for (int i=1; i<=n; i++)  //枚舉上邊 
    {
        if (a[i].x-a[l].x>x)
        {
            if (WORK(l,i-1)) return true;
            while (a[i].x-a[l].x>x) l++;
        }
    }
    if (WORK(l,n)) return true;
    return false;
}
int main()
{
    freopen("square.in","r",stdin);
    freopen("square.out","w",stdout);
    scanf("%d%d",&C,&n);
    for (i=1; i<=n; i++)
        scanf("%d%d",&a[i].x,&a[i].y);
    sort(a+1,a+n+1,cmp);
    L=0; R=10000; mid=(L+R)/2;
    while (L<=R)  //二分答案 
    {
        if (OK(mid)) {R=mid-1; mid=(L+R)/2;} else
        {
            L=mid+1;
            mid=(L+R)/2;
        }
    }
    cout<<L+1;
    return 0;
}

（3）第三題^{這是不是我第一次決定把第三題也寫下來...}

追逐(chase)

Time Limit:1000ms?? Memory Limit:128MB

題目描述

這次，LYK以一個上帝視角在看豹子賽跑。

在一條無線長的跑道上，有n只豹子站在原點。第i只豹子將在第ti個時刻開始奔跑，它的速度是vi/時刻。

因此在不同的時刻，這n只豹子可能在不同的位置，并且它們兩兩之間的距離也將發生變化。

LYK覺得眼光八方太累了，因此它想找這么一個時刻，使得最遠的兩只豹子的距離盡可能近，當然這不能是第0時刻或者第0.01時刻。它想知道的是最遲出發的豹子出發的那一刻開始，離得最遠的兩只豹子在距離最小的時候這個距離是多少。

當然這個時刻不僅僅可能發生在整數時刻，也就是說可能在1.2345時刻這個距離最小。

輸入格式(chase.in)

??? 第一行一個數n。

??? 接下來n行，每行兩個數分別是ti和vi。

輸出格式(chase.out)

??? 輸出一個數表示答案，你只需保留小數點后兩位有效數字就可以了。

輸入樣例

3

1 4

2 5

3 7

輸出樣例

0.33

樣例解釋

在第5+2/3這個時刻，第一只豹子在18+2/3這個位置，第二只豹子在18+1/3這個位置，第三只豹子在18+2/3這個位置，最遠的兩只豹子相距1/3的距離，因此答案是0.33。

數據范圍

對于20%的數據n=2。

對于20%的數據n=3

對于60%的數據n<=100。

對于80%的數據n<=1000。

對于100%的數據n<=100000，1<=vi,ti<=100000。

這道題本來是棄了，后來發現20%還是很好寫的。然后就寫了一下。結果迷之運行時錯誤。（所以代碼就不放了）

正解思路：

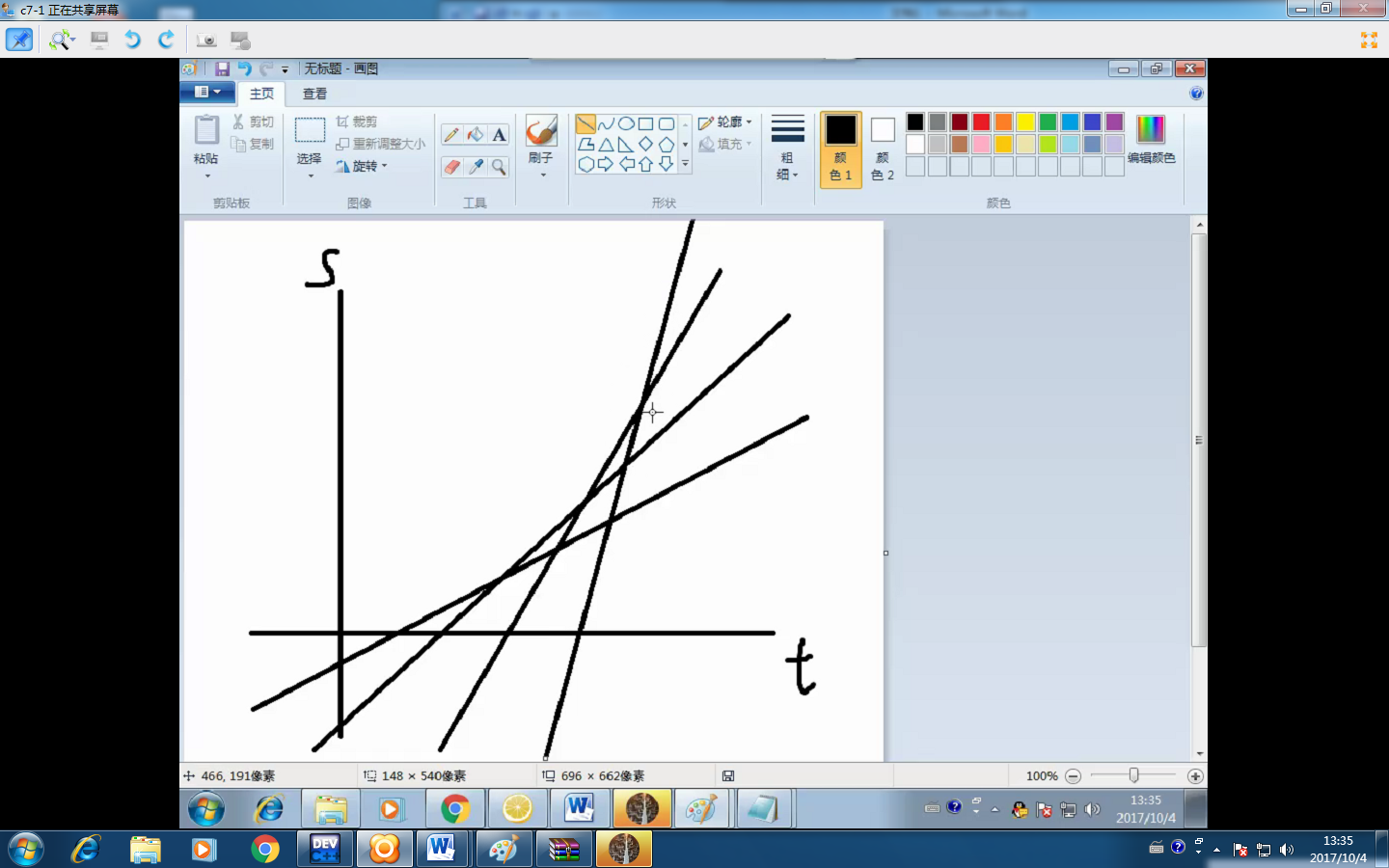
假如一條直線代表一只豹砸

?

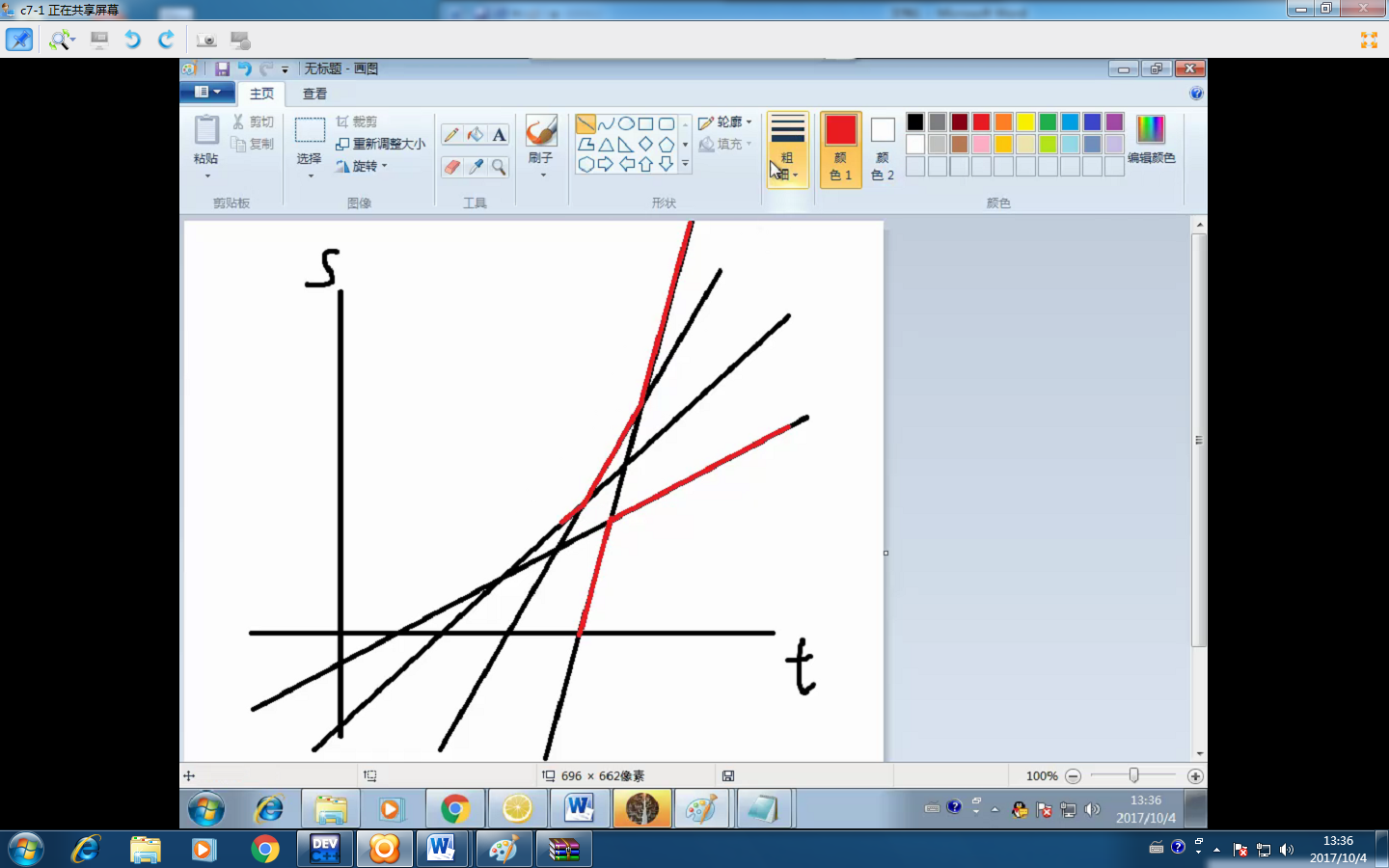
可以分別描出每一時刻離原點最近和最遠的豹砸

?

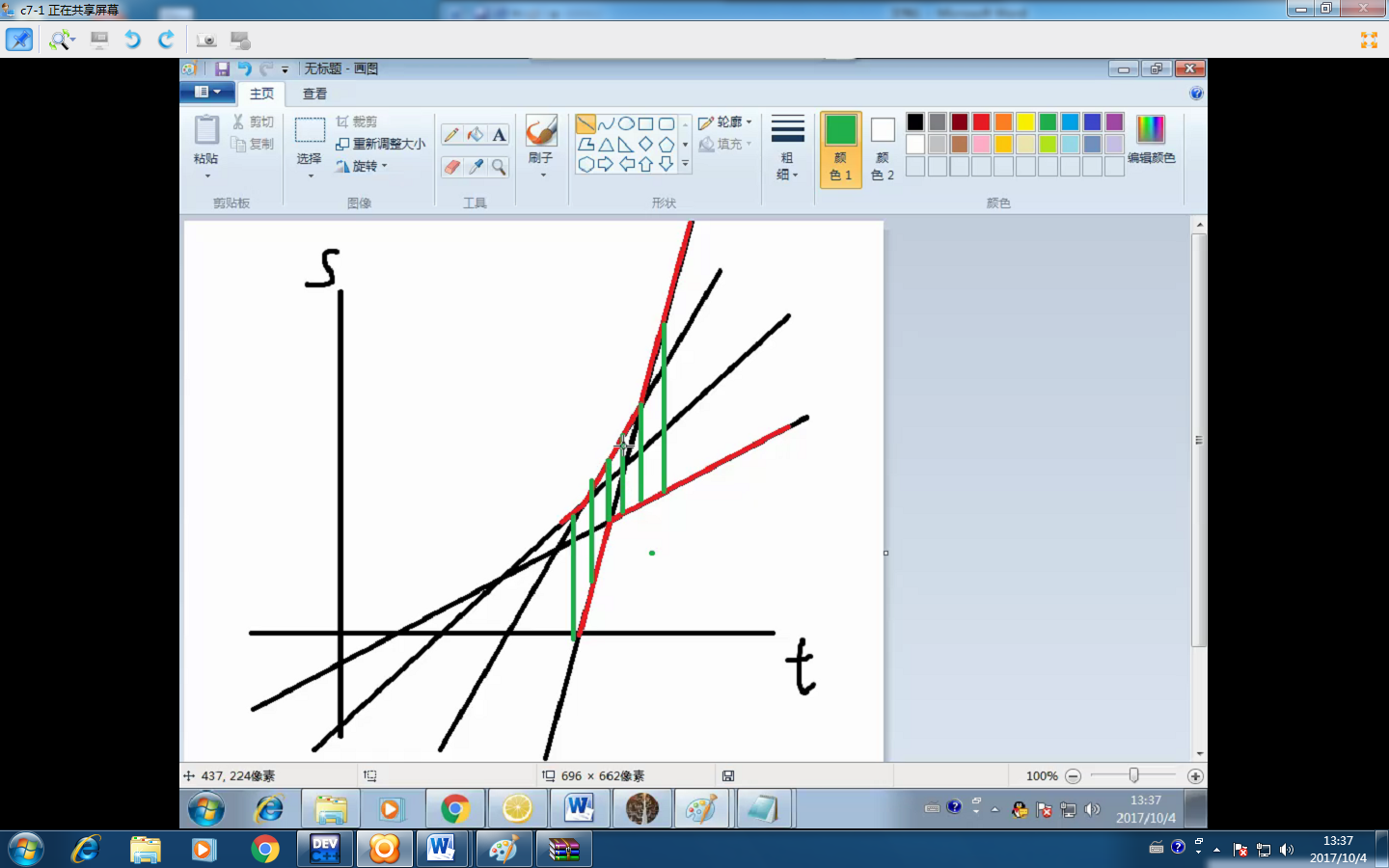
綠色部分就是他們的差，題目要求找的就是最短的綠線。

易證綠色的只會在交點處最小

60分算法:求出所有交點，然后再求每只豹砸

?

?

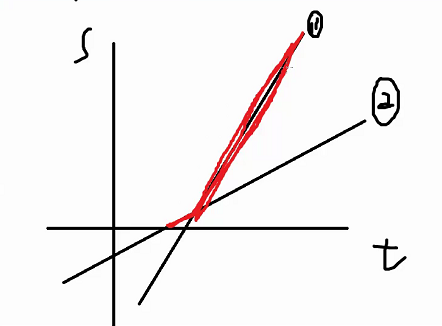
排除掉跑得慢又跑的晚的豹子后，我們發現斜率大的豹子占據右邊一段

用單調棧實現

?

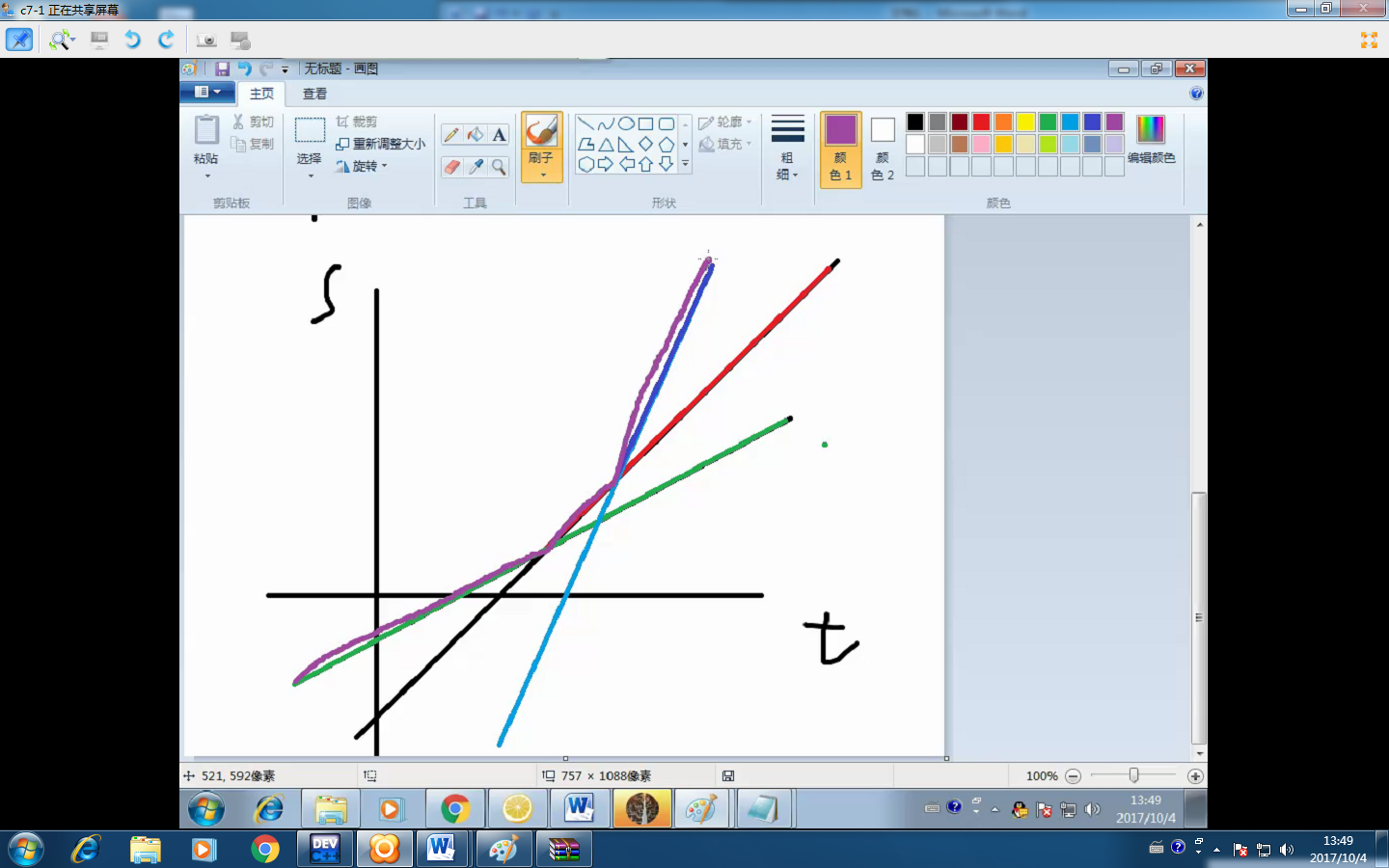
如圖，三條斜率不同的線段最后的上凸殼是紫色部分。也就是說，在這種情況下，每遇到一個交點上凸殼方向就會改變。

?

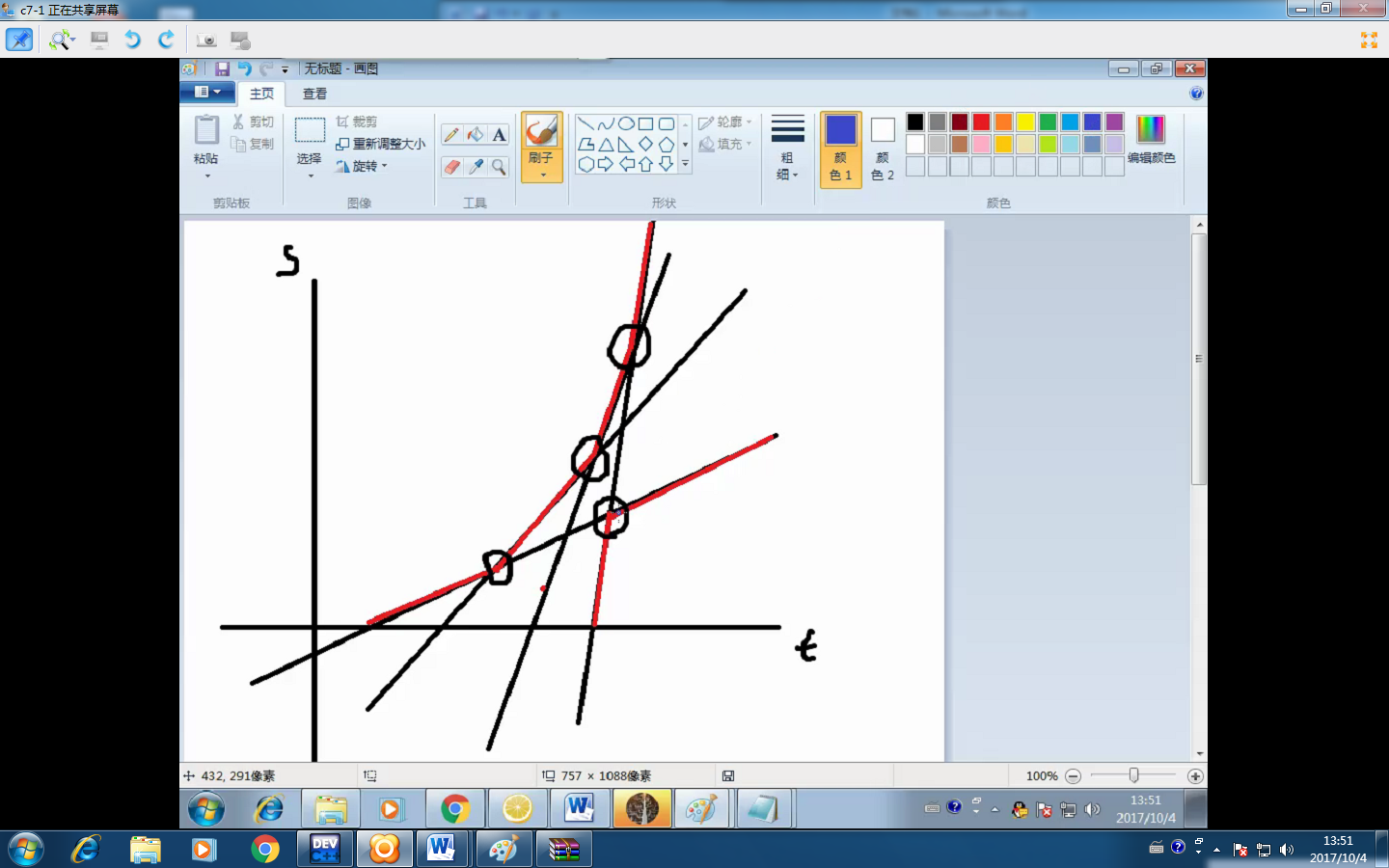
下凸殼同理：對于兩只豹子，一只跑得慢且后跑，一只跑得快一開始就跑。我們保留前面那只。

上凸殼流程：

1. 插入一條線，把所有值都先賦給第一條線；
2. 插入第二條線，把向上拐的那一段交給第二條線保管（也就是縫交點變保管線段）
3. 以此類推…

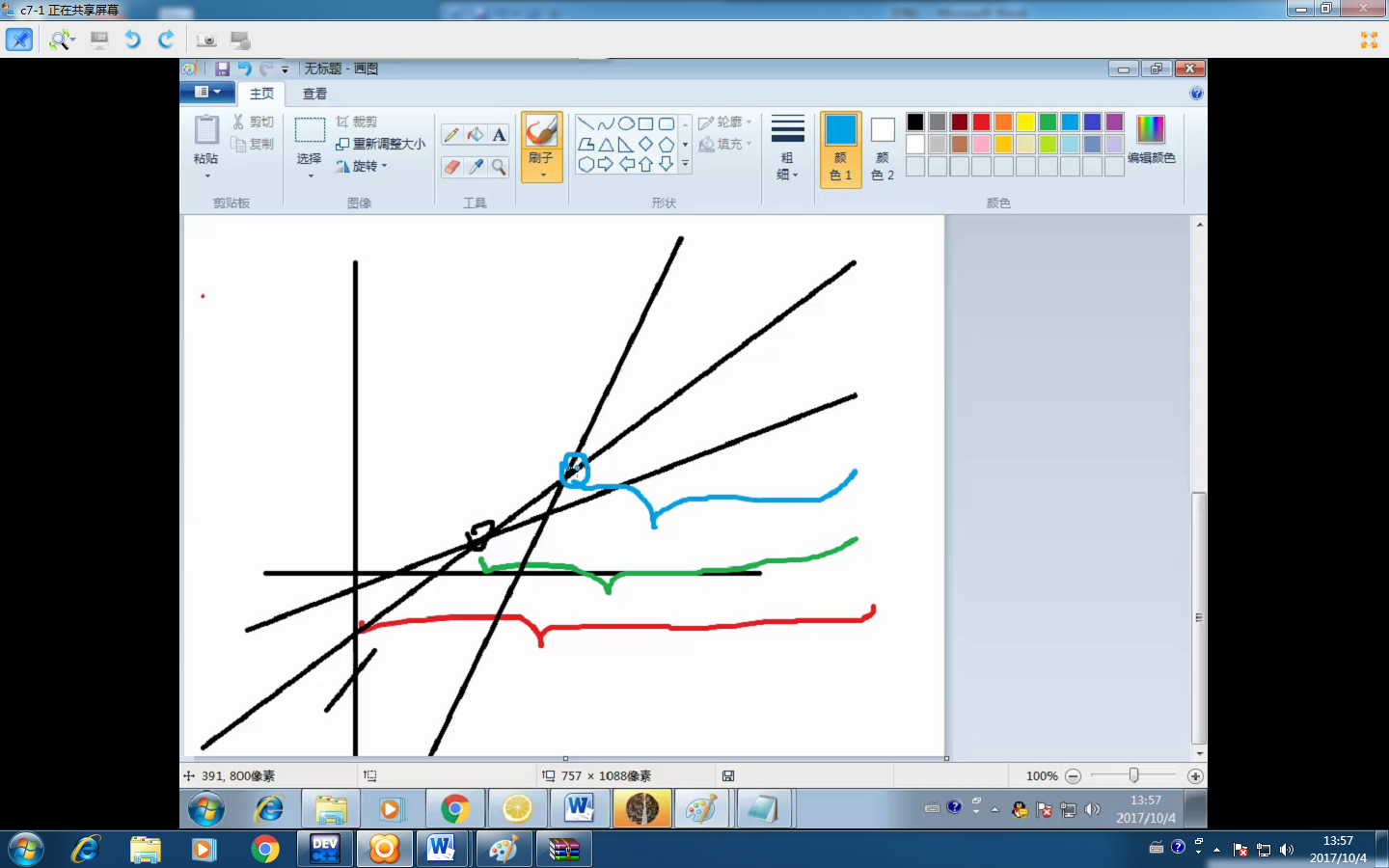
標程（可以說是很可怕了）：

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>

using namespace std;
const long double INF=(long double)1000000000*10;
long double L,R,mid,ans,hh[100005];
int r,rr,i,n,MAX,X,Y,cnt,vv[100005],vv2[100005];
struct node2 {int t; long double l;} s[200005],S[200005];
struct node {int t,v;} t[100005];
int cmp(node i,node j) {return i.v<j.v || i.v==j.v && i.t>j.t;}
struct Node {long double x;int y,z;} p[200005];
int CMP(Node i,Node j) {return i.x<j.x;}
long double work(int x,long double y) {return (long double)t[x].v*y-hh[x];}
int main()
{
    freopen("chase.in","r",stdin);
    freopen("chase.out","w",stdout);
    while (1)
    {
        scanf("%d",&n);
       // if (n==0) return 0;
        MAX=0;
        for (i=1; i<=n; i++)
        {
            scanf("%d%d",&t[i].t,&t[i].v);
            MAX=max(MAX,t[i].t);
        }
        sort(t+1,t+n+1,cmp); int MIN=t[n].t;
        for (i=n-1; i>=2; i--)
        {
            if (t[i].t>MIN) vv[i]=1; else
            MIN=t[i].t,vv[i]=0;
        }
        for (i=1; i<=n; i++) hh[i]=(long double)t[i].t*t[i].v;
        r=1; s[1].l=MAX; s[1].t=1; s[2].l=INF; vv[n]=0;
        for (i=2; i<=n; i++)
        if (!vv[i])
        {
            while (r && work(i,s[r].l)>=work(s[r].t,s[r].l)) r--;
            if (!r) {r=1; s[1].l=MAX; s[1].t=i; continue;}
            L=s[r].l; R=s[r+1].l; mid=(L+R)/2.0;
            for (int I=1; I<=80; I++)
            {
                if (work(i,mid)>=work(s[r].t,mid)) {R=mid; mid=(L+R)/2.0;} else {L=mid; mid=(L+R)/2.0;}
            }
            s[++r].l=mid; s[r].t=i; s[r+1].l=INF;
        }
        rr=1; S[1].l=MAX; S[2].l=INF; S[1].t=n;
        MIN=t[1].t;
        for (i=2; i<n; i++)
          if (t[i].t<MIN) vv2[i]=1; else
            MIN=t[i].t,vv2[i]=0;
        for (i=n-1; i>=1; i--)
        if (!vv2[i])
        {
            while (rr && work(i,S[rr].l)<=work(S[rr].t,S[rr].l)) rr--;
            if (!rr) {rr=1; S[1].l=MAX; S[1].t=i; continue;}
            L=S[rr].l; R=S[rr+1].l; mid=(L+R)/2.0;
            for (int I=1; I<=80; I++)
            {
                if (work(i,mid)<=work(S[rr].t,mid)) {R=mid; mid=(L+R)/2.0;} else {L=mid; mid=(L+R)/2.0;}
            }
            S[++rr].l=mid; S[rr].t=i; S[rr+1].l=INF;
        }
        cnt=0;
        for (i=1; i<=r; i++) {p[++cnt].x=s[i].l; p[cnt].y=1; p[cnt].z=s[i].t;}
        for (i=1; i<=rr; i++) {p[++cnt].x=S[i].l; p[cnt].y=0; p[cnt].z=S[i].t;}
        sort(p+1,p+cnt+1,CMP); X=Y=0; ans=INF;  //X是上凸指針Y是下凸指針 
        for (i=1; i<=cnt; i++)  //遇到上凸X動，遇到下凸Y動 
        {
            if (p[i].y==1) X=p[i].z; else Y=p[i].z;
          //  printf("%.5f\n",(double)p[i].x);
            if (X && Y) ans=min(ans,work(X,p[i].x)-work(Y,p[i].x));
        }
        printf("%.2f\n",fabs((double)ans));
        return 0;
    }
}

---

今日專題——圖論

圖論

??????????????????????????? ——算法簡單，難點在于構圖

l? 競賽圖：任意兩個人（點）打一場比賽，由贏的向輸的連一條邊。

l? 鄰接表的實現：

cin>>u>>v; (u->v)

f[u][++f[u][0]]=v;

?

f[u][0]表示u連出去能到幾個點

f[u][i]表示u連出去第i個點是啥

?

l? 鄰接表的好處：在遍歷一個點能連向哪些點時，復雜度是出度，而不是O(n)

l? 鄰接矩陣的好處：判斷一條邊是否存在，查詢一條邊的權值，復雜度是O(1)

l? 邊表（前向星）：

cin>>u>>v;

o++;

e[o]=v;? (u->v)? 之前u還指向過一些點 head[u]來表示起點為u的邊編號最大的那個編號是多少

next[o]=head[o]?? 當u處理完連向v的這條邊之后，下一次處理的邊編號是多少

head[u]=o;

?

便利u為起點，能連向哪些點

For(int i=head[u];i!=0;)

?

l? 拓撲排序

給定一張拓撲圖，求1號點走到n號點的方案總數

?

令dp[i]表示從1號點走到i號點的方案總數

有dp[i]=xigma(dp[j]) (j->i)

枚舉i時，按照拓撲序進行枚舉

Dp[n]就是答案

?

l? 最短路

1. Dijkstra

（1）令dis[i]表示當前u到i的最短路是多少。

（2）將dis[u]=0,dis[i]=inf(i!=u)。

（3）尋找最小的dis[x]且x曾經沒被找到過。

（4）若x=v，輸出答案并退出。

（5）枚舉x的所有邊，用dis[x]去更新其余dis[]，回到步驟②。

時間復雜度為n^2。

使用范圍：不存在負權邊。

2. SPFA（poj1502）

1. 令dis[i]表示當前u到i的最短路是多少。
2. ①將dis[u]=0,dis[i]=inf(i!=u)，并將u加入隊列中。
3. ②設當前隊首為x，枚舉x。
4. ③枚舉x的所有邊，用dis[x]去更新其余dis[]，若dis[i]此時被更新且i當前不在隊列中，將其加入隊列。
5. ④將x彈出隊列，若此時隊列為空，結束，否則返回步驟②。

?

l? 并查集

?

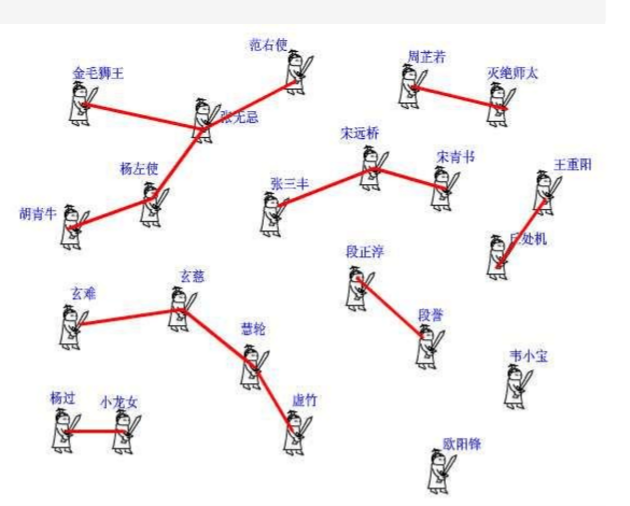
一行并查集(實現了路徑壓縮)：

Int getf(int x) {return f[x]=x?f[x]:f[x]=getf(f[x]);}?? //不斷找father

?

l? 最小生成樹

1.Prim：一開始隨便找一個點當做集合中點，每次找一條最短的邊，要求這條邊鏈接的兩個點，一個在集合中，一個不在集合中。把連接的另一個點和這條邊加入到集合中。

2.kruskal：對邊權進行排序，每次加入后判斷是否存在環，若不存在環，則加入（并查集實現）

?

l? 二分圖（不存在奇環，即有奇數個點的環）

二分圖染色：（col[i]=1->i這個點染成黑色 col[i]=2->i這個點染成白色 col[i]=0->i這個點還未被染色）

Vector <int> v[N];

Void dfs(int x,int y)

{

Col[x]=y;

For(int i=0;i<v[x].size();i++)

{

??? If(!col[v[x][i]]) dfs(v[x][i],3-y);

If(col[v[x][i]]==col[x]) FLAG=true;? //如果一條邊連接的兩個點是同一種顏色，這是不被允許的（判定方法1）

}

}

For(int i=1;i<=n;i++) col[i]=0;

For(int i=1;i<=n;i++) if(!col[i])dfs(i,1);

if(FLAG) cout<<’no’; else cout<<’yes’;

二分圖判定方法2：

• 將每個點A裂成兩個點A與A’。
• 若A與B之間存在邊，則連一條A與B’的邊，A’與B的邊。
• 若此時A與A’連通，或者B與B’連通，則該圖不是二分圖。（若連通則必然出現了奇環）
• 利用并查集實現即可。

?

?

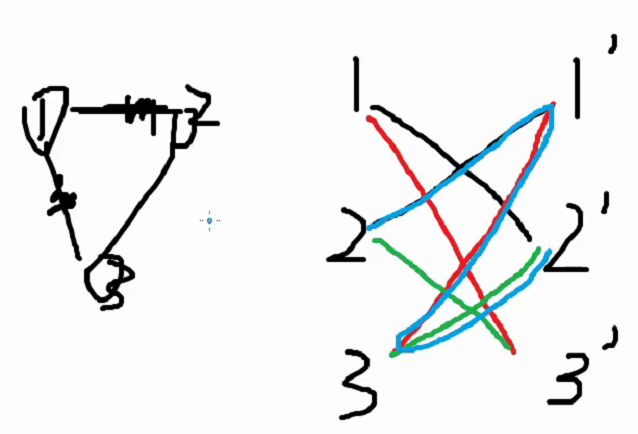
[圖例解釋]標記完成后，若發現2與2`連通了，則不是二分圖（奇環）

可通過染色來理解，會出現矛盾

For(int i=1;i<=n;i++) p[i][0]=++cnt,p[i][1]=++cnt;

For(int i=2;i<=cnt;i++) f[i]=I;

For(int i=1;i<=m;i++)

{

u-v

f[getf(p[u][0])]=getf(p[v][1]);

f[getf(p[u][1])=getf(p[v][0]);

if(getf(p[u][0])==getf(p[u][1])||getf(p[v][0])==getf(p[v][1]))FLAG=true;

}

l? 二分圖最大匹配

匈牙利算法：

?

?

l? 強連通分量：任意兩個點之間相互可達

l? DPN時間戳（第幾次被DFS到）

l? ***LOW LOW[i] i及i的所有子孫能訪問到的最小時間戳

?

求極大強連通分量（Tarjan）：

Void dfs(int x)

{

DFN[x]=++Time;Low[x]=DFN[x];

St[++r]=x; /*壓入棧*/int R=r; V[x]=true;

For(int i=0;i<v[x].size();i++) //枚舉x能連向哪些點

{

?if(!DFN[v[x][i]]){dfs(v[x][i]);LOW[x]=min(LOW[x],LOW[v[x][i]]);}? //如果當前點還沒dfs過，就dfs一遍。同時更新時間戳

???? if(V[v[x][i]])LOW[x]=min(LOW[x],DFN[v[x][i]]);

}

If(LOW[x]==DFN[x])

{

cnt++;

??? For(int i=R;i<=r;i++) p[st[i]]

r=R-1;

}

}

cnt 第cnt個強連通分量??? p[i] i所處的的事哪個極大強連通分量

LOW[x]==DFN[x] 已出現一個極大強連通分量

?

**背代碼最開始每天都要默一遍**

?

今天信息量簡直太大，腦袋要炸掉了。。