Sigmoid函數

Sigmoid函數計算公式

$f(x) = \frac{1}{1+e^{-x}}$

sigmoid：x取值范圍(-∞，+∞)，值域是(0, 1)。

sigmoid函數求導

這是sigmoid函數的一個重要性質。

$\begin{aligned}g(z)&=\frac{1}{1+e^{-z}} \\g'(z)&=(\frac{1}{1+e^{-z}})' \\&=\frac{e^{-z}}{(1+e^{-z})^2} \\&=\frac{1}{1+e^{-z}}\cdot\frac{e^{-z}}{1+e^{-z}} \\&=\frac{1}{1+e^{-z}}\cdot(1-\frac{1}{1+e^{-z}}) \\&=g(z)\cdot(1-g(z))\end{aligned}$

圖像

?¨è?é??￥????è?°

代碼

# -*- coding: utf-8 -*-
"""
@author: tom
"""import numpy
import math
import matplotlib.pyplot as pltdef sigmoid(x):a = []for item in x:a.append(1.0/(1.0 + math.exp(-item)))return ax = numpy.arange(-10, 10, 0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.show()

當x為0時，Sigmoid函數值為0.5。隨著x的增大，對應的Sigmoid值將逼近于1；而隨著x的減小，Sigmoid值將逼近于0。兩種坐標尺度下的Sigmoid函數圖。上圖的橫坐標為-5到5，這時的曲線變化較為平滑；下圖橫坐標的尺度足夠大，可以看到，在x = 0點處Sigmoid函數看起來很像階躍函數，如果橫坐標刻度足夠大（上圖中的下圖），Sigmoid函數看起來很像一個階躍函數。

sigmoid函數的性質

sigmoid函數是一個閥值函數，不管x取什么值，對應的sigmoid函數值總是0<sigmoid(x)<1。
sigmoid函數嚴格單調遞增，而且其反函數也單調遞增
sigmoid函數連續
sigmoid函數光滑
sigmoid函數關于點(0, 0.5)對稱
sigmoid函數的導數是以它本身為因變量的函數，即f(x)' = F(f(x))

sigmoid函數Logistic函數

對于分類問題，需要找到一個單調可微函數將真實值與廣義線性回歸模型的預測值聯系起來，這個函數就是Logistic函數，或者稱Sigmoid函數。（單位階躍函數不連續，且瞬間跳躍的過程很難處理）

原因參考https://zhuanlan.zhihu.com/p/59137998

Logistic/Sigmoid函數是一個常見的S型函數，適合于提供概率的估計以及依據這些估計的二進制響應；由于其單調遞增、反函數單調遞增、任意階可導等性質，且可以將變量映射到(0, 1)之間，在邏輯回歸、神經網絡中有著廣泛的應用。

sigmod作為激活函數優缺點

優點：

Sigmoid的取值范圍在(0, 1)，而且是單調遞增，比較容易優化
Sigmoid求導比較容易，可以直接推導得出。

缺點：

Sigmoid函數收斂比較緩慢
容易飽和（就是梯度消失之后，使用BP算法優化時這個神經元沒有變化）和終止梯度傳遞(“死神經元”)；
Sigmoid函數并不是以（0,0）為中心點
?

tanh函數(雙曲正切函數)

tanh為雙曲正切函數，過（0,0）點。相比Sigmoid函數，更傾向于用tanh函數

$f(x) = tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

x取值范圍(-∞，+∞)，值域是(-1, 1)。

tanh求導

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? $\begin{aligned}\cfrac{?{\rm d}y}{?{\rm d}x} &= \left(\cfrac{e^x-e^{-x}}{e^x+e^{-x}}\right)^\prime \\&= \cfrac{(e^x-e^{-x})^\prime(e^x+e^{-x})-(e^x-e^{-x})(e^x+e^{-x})^\prime}{(e^x+e^{-x})^2} \\&= \cfrac{(e^x+e^{-x})(e^x+e^{-x})-(e^x-e^{-x})(e^x-e^{-x})}{(e^x+e^{-x})^2} \\&= \cfrac{e^{2x}+e^{-2x}+2-(e^{2x}+e^{-2x}-2)}{(e^x+e^{-x})^2} \\&= \cfrac{4}{(e^x+e^{-x})^2} \end{aligned}$

又因為

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? $1 - y = 1 - \cfrac{e^x-e^{-x}}{e^x+e^{-x}} = \cfrac{e^x+e^{-x}-(e^x-e^{-x})}{e^x+e^{-x}} = \cfrac{2e^{-x}}{e^x+e^{-x}}$
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $1 + y = 1 + \cfrac{e^x-e^{-x}}{e^x+e^{-x}} = \cfrac{e^x+e^{-x}+(e^x-e^{-x})}{e^x+e^{-x}} = \cfrac{2e^{x}}{e^x+e^{-x}}$

所以

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? $(1 - y)(1+y) = 1 - y^2 = \cfrac{4}{(e^x+e^{-x})^2} = \cfrac{?{\rm d}y}{?{\rm d}x}$

即： $y = {\rm tanh}^\prime(x)=1-{\rm tanh}^2(x)$

或者

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $f(x)=\frac{sinh(x)}{cosh(x)}=\frac{1-e^{-2x}}{1+e^{-2x}}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}=2sigmoid(2x)-1$

? ? ? ? ? ? ? ? ? ? ? ? ? ?? $f^{'}(x)=tanh{'}(x)=sech^{2}(x)=1-tanh^{2}(x)$

tanh優缺點

優點：

輸出以（0,0）為中心、取值范圍(-1~1)、易理解
收斂速度相對于Sigmoid更快

缺點：

該導數在正負飽和區的梯度都會接近于 0 值，會造成梯度消失。還有其更復雜的冪運算。

圖像

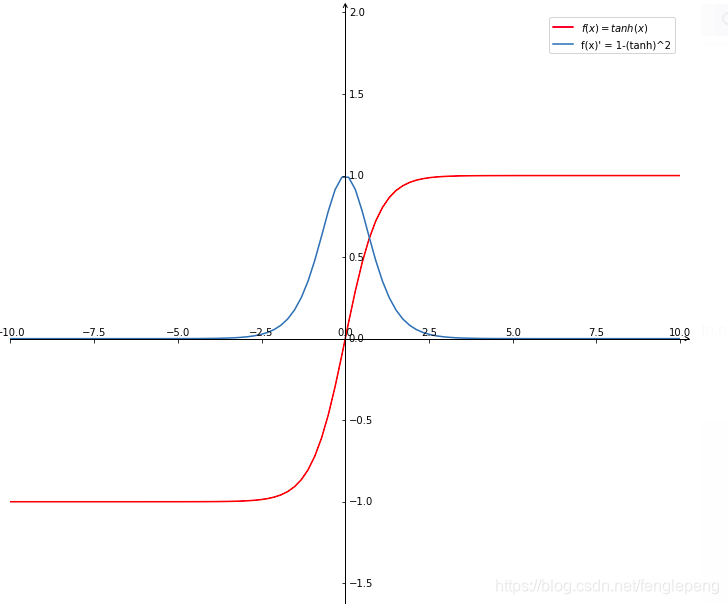
代碼

import math
import matplotlib.pyplot as plt
import numpy as np
import mpl_toolkits.axisartist as axisartist# Tanh 激活函數
class Tanh:       # 原函數 def forward(self, x):return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))# 導數def backward(self, outx):tanh = (np.exp(outx) - np.exp(-outx)) / (np.exp(outx) + np.exp(-outx))return 1 - math.pow(tanh, 2)# 畫圖
def Axis(fig, ax):#將繪圖區對象添加到畫布中fig.add_axes(ax)# 隱藏坐標抽ax.axis[:].set_visible(False)# new_floating_axis 創建新的坐標ax.axis["x"] = ax.new_floating_axis(0, 0)# 給 x 軸創建箭頭線，大小為1.0ax.axis["x"].set_axisline_style("->", size = 1.0)# 給 x 軸箭頭指向方向ax.axis["x"].set_axis_direction("top")# 同理，創建 y 軸ax.axis["y"] = ax.new_floating_axis(1, 0)ax.axis["y"].set_axisline_style("->", size = 1.0)ax.axis["y"].set_axis_direction("right")# 返回間隔均勻的100個樣本，計算間隔為[start, stop]。
x =  np.linspace(-10, 10, 100)
y_forward = []
y_backward = []def get_list_forward(x):for i in range(len(x)):y_forward.append(Tanh().forward(x[i]))return y_forwarddef get_list_backward(x):for i in range(len(x)):y_backward.append(Tanh().backward(x[i]))return y_backwardy_forward = get_list_forward(x)
y_backward = get_list_backward(x)#創建畫布
fig = plt.figure(figsize=(12, 12))#創建繪圖對象ax
ax = axisartist.Subplot(fig, 111)
Axis(fig, ax)# 設置x, y軸范圍
plt.ylim((-2, 2))
plt.xlim((-10, 10))# 原函數，forward function
plt.plot(x, y_forward, color='red', label='$f(x) = tanh(x)$')
plt.legend()# 導數， backward function
plt.plot(x, y_backward, label='f(x)\' = 1-(tanh)^2')
plt.legend()plt.show()

ReLU函數(The Rectified Linear Unit, 修正線性單元函數)

公式如下：

$ReLU = f(x) = max(0,x)=\left\{\begin{matrix} 0,x\leq 0\\x,x>0 \end{matrix}\right.$

${f(x)}' =\left\{\begin{matrix} 0,x\leq 0\\1,x>0 \end{matrix}\right.$

圖形圖像：對于輸入的x以0為分界線，左側的均為0，右側的為y=x這條直線

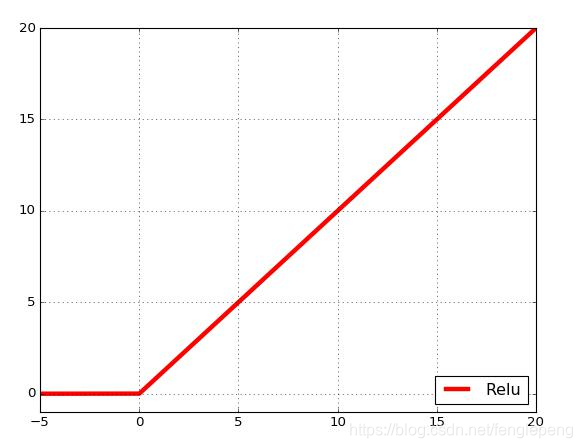
優缺點

優點：

在SGD中收斂速度要比Sigmoid和tanh快很多
梯度求解公式簡單，不會產生梯度消失和梯度爆炸
對神經網絡可以使用稀疏表達
對于無監督學習，也能獲得很好的效果

缺點：

沒有邊界，可以使用變種ReLU: min(max(0,x), 6)
比較脆弱，比較容易陷入出現”死神經元”的情況，比如我們設置一個特別大學習率，經過一次更新權重參數w之后，w對于后續所有的輸入x的結果都小于0，這個時候再進過relu激活，輸出還是0，就會造成這個ReLU神經元對后來來的輸入永遠都不會被激活，同時，在反向傳播時，在計算這個神經元的梯度永遠都會是0，造成不可逆的死亡。（解決方案：較小的學習率）

ReLU函數是從生物學角度，模擬出腦神經元接收信號更加準確的激活模型。相比于Sigmoid函數，具有以下優點：

單側抑制；
相對寬闊的興奮邊界；
稀疏激活性；
更快的收斂速度；

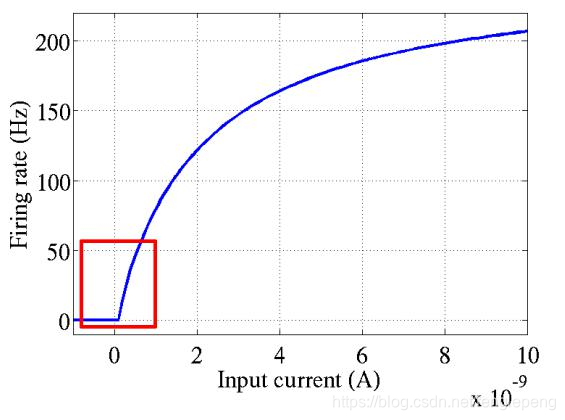
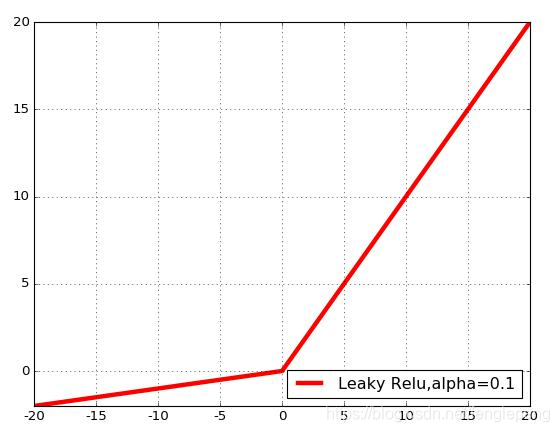
Leaky ReLU激活函數：

在ReLU函數的基礎上，對x≤0的部分進行修正；目的是為了解決ReLU激活函數中容易存在的”死神經元”情況的；不過實際場景中：效果不是太好。

$Leaky ReLU = f(x) = max(0,x)=\left\{\begin{matrix} ax,x\leq 0\\x,x>0 \end{matrix}\right.$

${f(x)}' =\left\{\begin{matrix} a,x\leq 0\\1,x>0 \end{matrix}\right.$

ELU激活函數：

指數線性激活函數，同樣屬于對ReLU激活函數的x≤0部分的轉換進行指數修正，而不是和Leaky ReLU中的線性修正。

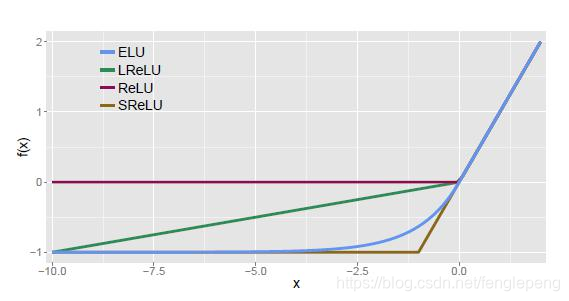
$ELU = f(x) = max(0,x)=\left\{\begin{matrix} a(e^x-1),x\leq 0\\x,x>0 \end{matrix}\right.$

${f(x)}' =\left\{\begin{matrix} f(x)+a,x\leq 0\\1,x>0 \end{matrix}\right.$

Maxout激活函數：

參考：https://arxiv.org/pdf/1302.4389.pdf

$maxout=f(x)=max_{j\in [1,k]}\{w_{j}x+b_{j}\}$

可以看作是在深度學習網絡中加入一層激活函數層，包含一個參數k，擬合能力特別強。特殊在于：增加了k個神經元進行激活，然后輸出激活值最大的值。

優點：

計算簡單，不會出現神經元飽和的情況
不容易出現死神經元的情況

缺點：

參數double，計算量復雜了

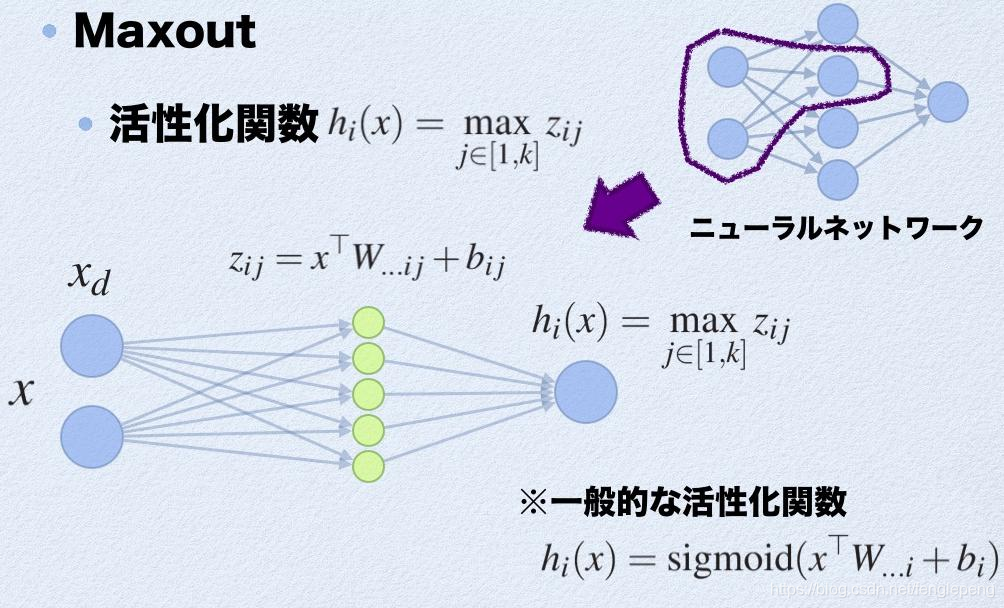
激活值 out = f(W.X+b); f是激活函數。’.’在這里代表內積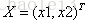這里寫圖片描述 ; W = () ?那么當我們對（i+1）層使用maxout（設定k=5）然后再輸出的時候，情況就發生了改變

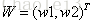
此時網絡形式上就變成上面的樣子，用公式表現出來就是：?

z1 = W1.X+b1;?
z2 = W2.X+b2;?
z3 = W3.X+b3;?
z4 = W4.X+b4;?
z5 = W4.X+b5;?
out = max(z1,z2,z3,z4,z5);?

也就是說第（i+1）層的激活值計算了5次，可我們明明只需要1個激活值，那么我們該怎么辦？其實上面的敘述中已經給出了答案，取這5者的最大值來作為最終的結果。?

總結一下，maxout明顯增加了網絡的計算量，使得應用maxout的層的參數個數成k倍增加，原本只需要1組就可以，采用maxout之后就需要k倍了。?

軟飽和和硬飽和

假設h（x）是一個激活函數。

當我們的n趨近于正無窮，激活函數的導數趨近于0，那么我們稱之為右飽和。
當我們的n趨近于負無窮，激活函數的導數趨近于0，那么我們稱之為左飽和。
當一個函數既滿足左飽和又滿足右飽和的時候我們就稱之為飽和，典型的函數有Sigmoid，Tanh函數。
對于任意的x，如果存在常數c，當x>c時，恒有=0，則稱其為右硬飽和。如果對于任意的x，如果存在常數c，當x<c時，恒有=0,則稱其為左硬飽和。既滿足左硬飽和又滿足右硬飽和的我們稱這種函數為硬飽和。
對于任意的x，如果存在常數c，當x>c時，恒有趨近于0，則稱其為右軟飽和。如果對于任意的x，如果存在常數c，當x<c時，恒有趨近于0,則稱其為左軟飽和。既滿足左軟飽和又滿足右軟飽和的我們稱這種函數為軟飽和。
?