深度學習之邊框回歸(Bounding Box Regression)

從rcnn， fast rcnn, faster rcnn, yolo, r-fcn, ssd，到cvpr的yolo9000。這些paper中損失函數都包含了邊框回歸，除了rcnn詳細介紹了，其他的paper都是一筆帶過，或者直接引用rcnn就把損失函數寫出來了。前三條網上解釋比較多，后面的兩條我看了很多paper，才得出這些結論。

為什么要邊框回歸？
什么是邊框回歸？
邊框回歸怎么做的？
邊框回歸為什么寬高，坐標會設計這種形式？
為什么邊框回歸只能微調，在離Ground Truth近的時候才能生效？

為什么要邊框回歸？

這里引用王斌師兄的理解，如下圖所示：
在這里插入圖片描述

對于上圖，綠色的框表示 Ground Truth, 紅色的框為 Selective Search 提取的 Region Proposal。那么即便紅色的框被分類器識別為飛機，但是由于紅色的框定位不準(IoU<0.5)，那么這張圖相當于沒有正確的檢測出飛機。如果我們能對紅色的框進行微調，使得經過微調后的窗口跟 Ground Truth 更接近，這樣豈不是定位會更準確。確實，Bounding-box regression 就是用來微調這個窗口的。

邊框回歸是什么？

對于窗口一般使用四維向量 $(x, y, w, h)$ 來表示，分別表示窗口的中心點坐標和寬高。對于下圖, 紅色的框 P 代表原始的 Proposal, 綠色的框 G 代表目標的 Ground Truth，我們的目標是尋找一種關系使得輸入原始的窗口 P 經過映射得到一個跟真實窗口 G 更接近的回歸窗口 $G^\hat{G}$ 。

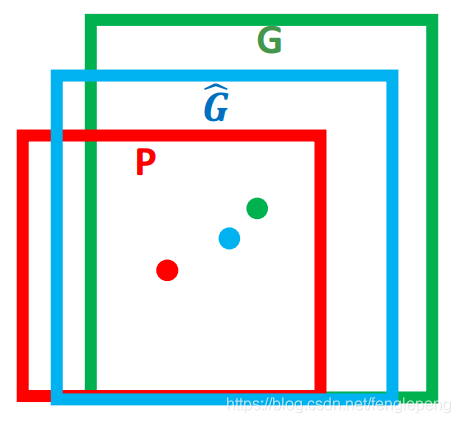
邊框回歸的目的既是：給定 $P_{x},P_{y},P_{w},P_{h})$ 尋找一種映射 $f$ ，使得 $f(Px,Py,Pw,Ph)=(Gx^,Gy^,Gw^,Gh^)f(P_{x},P_{y},P_{w},P_{h}) = (\hat{G_x},\hat{G_y},\hat{G_w},\hat{G_h})$ 并且 $(Gx^,Gy^,Gw^,Gh^)≈(Gx,Gy,Gw,Gh)(\hat{G_x},\hat{G_y},\hat{G_w},\hat{G_h}) \approx (G_{x},G_{y},G_{w},G_{h})$

邊框回歸怎么做的？

RCNN論文：Region-based Convolution Networks for Accurate Object detection and Segmentation

作者在完成了的生成候選區域——CNN提取特征——SVM進行分類以后，為了進一步的提高定位效果，在文章的附錄C中介紹了 Bounding-box Regression 的處理。Bounding-box Regression 訓練的過程中，輸入數據為N個訓練對 ${(P^{i},G^{i})},i=1,2,...,N$ ，其中 $pi=(pxi,pyi,pwi,phi)p^i=(p^i_x,p^i_y,p^i_w,p^i_h)$ 為proposal的位置，前兩個坐標表示proposal的中心坐標，后面兩個坐標分別表示proposal的width和height，而 $G^i=(G_x,G_y,G_w,G_h)$ 表示groundtruth的位置， regression的目標就是學會一種映射將P轉換為G。

那么經過何種變換才能從上圖中的窗口 P 變為窗口 $G^\hat{G}$ 呢？比較簡單的思路就是: 平移+尺度放縮

作者設計了四種坐標映射方法，其中前兩個表示對 proposal 中心坐標的尺度不變的平移變換，后面兩個則是對 proposal 的 width 和 height 的對數空間的變換，

先做平移 $(Δx,Δy)(\Delta x,\Delta y)$ ， $Δx=Pwdx(P),Δy=Phdy(P)\Delta x = P_{w}d_{x}(P),\Delta y = P_{h}d_{y}(P)$ 這是R-CNN論文的：( $d?(P)=w?TΦ5(P)=t?d_{ \ast }(P) = w_{ \ast }^{T}\Phi _{5}(P)=t_{ \ast }$ )

$G^x=Pwdx(P)+Px,(1)\hat{G}_{x} = P_{w}d_{x}(P) + P_{x},\text{(1)}$

$G^y=Phdy(P)+Py,(2)\hat{G}_{y} = P_{h}d_{y}(P) + P_{y},\text{(2)}$

然后再做尺度縮放 $S_{w},S_{h})$ , $S_{w} = exp(d_{w}(P)),S_{h} = exp(d_{h}(P))$ , 對應論文中：

$G^w=Pwexp(dw(P)),(3)\hat{G}_{w} = P_{w}exp(d_{w}(P)),\text{(3)}$

$G^h=Phexp(dh(P)),(4)\hat{G}_{h} = P_{h}exp(d_{h}(P)),\text{(4)}$

觀察(1)-(4)我們發現，邊框回歸學習就是 $d_{x}(P),d_{y}(P),d_{w}(P),d_{h}(P)$ 這四個變換。下一步就是設計算法那得到這四個映射。

線性回歸就是給定輸入的特征向量 X, 學習一組參數 W, 使得經過線性回歸后的值跟真實值 Y(Ground Truth)非常接近. 即 $\approx WX$ 。那么 Bounding-box 中我們的輸入以及輸出分別是什么呢？

Input:

$RegionProposal→P=(Px,Py,Pw,Ph)RegionProposal\rightarrow P = (P_{x},P_{y},P_{w},P_{h})$ ，這個是什么？輸入就是這四個數值嗎？不是，其實真正的輸入是這個窗口對應的 CNN 特征，也就是 R-CNN 中的 Pool5 feature（特征向量）。 (注：訓練階段輸入還包括 Ground Truth，也就是下邊提到的 $t?=(tx,ty,tw,th)t_{ \ast } = (t_{x},t_{y},t_{w},t_{h})$

Output:

outpue 為：需要進行的平移變換和尺度縮放 $d_{x}(P),d_{y}(P),d_{w}(P),d_{h}(P)$ ，或者說是 $Δx,Δy,Sw,Sh\Delta x,\Delta y,S_{w},S_{h}$ 。我們的最終輸出不應該是 Ground Truth 嗎？是的，但是有了這四個變換我們就可以直接得到 Ground Truth。

這里有個問題需要注意，根據(1)~(4)我們可以知道， P 經過 $d_{x}(P),d_{y}(P),d_{w}(P),d_{h}(P)$ 得到的并不是真實值 G，而是預測值 $G^\hat{G}$ 。

在訓練時這四個值 $Δx,Δy,Sw,Sh\Delta x,\Delta y,S_{w},S_{h}$ 的真實值應該是經過 Ground Truth 和 Proposal 計算得到的真正需要的平移量 $t_{x},t_{y})$ 和尺度縮放 $t_{w},t_{h})$ 。這也就是 R-CNN 論文中的(6)~(9)：

$t_{x} = (G_{x}?P_{x})/ P_{w},(6)$

$t_{y} = (G_{y}?P_{y})/ P_{h},(7)$

$t_{w} = \log ?(G_{w}/ P_{w}),(8)$

$t_{h} = \log ?(G_{h}/ P_{h}),(9)$

目標函數

目標函數可以表示為 $d?(P)=w?TΦ5(P)d_{ \ast }(P) = w_{ \ast }^{T}\Phi _{5}(P)$ ， $Φ5(P)\Phi _{5}(P)$ 是輸入 Proposal 的特征向量， $w?w_{ \ast }$ 是要學習的參數（*表示 x,y,w,h，也就是每一個變換對應一個目標函數） , $d?(P)d_{ \ast }(P)$ 是得到的預測值。我們要讓預測值跟真實值 $t?=(tx,ty,tw,th)t_{ \ast } = (t_{x},t_{y},t_{w},t_{h})$ 差距最小，得到損失函數為：

$Loss=∑iN(t?i?w^?T?5(Pi))2.Loss = \sum \limits_{i}^{N}(t_{ \ast }^{i}?\hat{w}_{ \ast }^{T}\phi _{5}(P^{i}))^2.$

函數優化目標為：

$W?=argminw?∑iN(t?i?w^?T?5(Pi))2+λ∣∣w^?∣∣2.W_{ \ast } = argmin_{w_{ \ast }} \sum \limits_{i}^{N}(t_{ \ast }^{i}?\hat{w}_{ \ast }^{T}\phi _{5}(P^{i}))^2 + \lambda ||\hat{w}_{ \ast }||^2.$

利用梯度下降法或者最小二乘法就可以得到 $w?w_{ \ast }$ 。

最終在進行實驗時，lambda = 1000, 同時作者發現同一對中P和G相距過遠時通過上面的變換是不能完成的，而相距過遠實際上也基本不會是同一物體，因此作者在進行實驗室，對于 pair(P,G) 的選擇是選擇離P較近的G進行配對，這里表示較近的方法是需要P和一個G的最大的IoU要大于0.6,否則則拋棄該P。

為什么寬高尺度會設計這種形式？

重點解釋一下為什么設計的 $t_{x},t_{y}$ 為什么除以寬高，為什么 $t_{w},t_{h}$ 會有log形式！！！

首先CNN具有尺度不變性，以下圖為例：
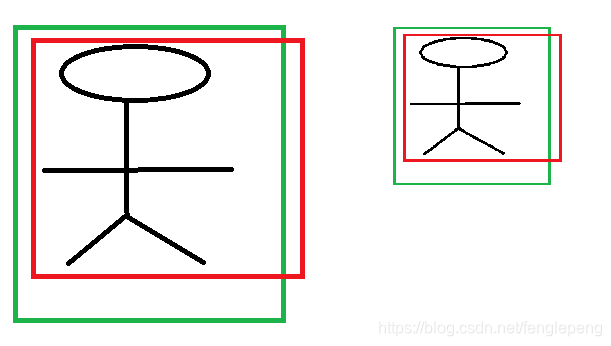
在這里插入圖片描述

x,y 坐標除以寬高

上圖的兩個人具有不同的尺度，因為他都是人，我們得到的特征相同。假設我們得到的特征為 $?1,?2\phi _{1},\phi _{2}$ ，那么一個完好的特征應該具備 $_{1} = \phi$ 。ok，如果我們直接學習坐標差值，以x坐標為例， $x_{i},p_{i}$ 分別代表第i個框的x坐標，學習到的映射為 $f$ , $f(?1)=x1?p1f(\phi _{1}) = x_{1}?p_{1}$ ，同理 $f(?2)=x2?p2f(\phi _{2}) = x_{2}?p_{2}$ 。從上圖顯而易見， $x1?p1≠x2?p1x_{1}?p_{1} \neq x_{2}?p_{1}$ 。也就是說同一個x對應多個y，這明顯不滿足函數的定義。邊框回歸學習的是回歸函數，然而你的目標卻不滿足函數定義，當然學習不到什么。

寬高坐標Log形式

我們想要得到一個放縮的尺度，也就是說這里限制尺度必須大于0。我們學習的 $t_{w},t_{h}$ 怎么保證滿足大于0呢？直觀的想法就是EXP函數，如公式(3), (4)所示，那么反過來推導就是Log函數的來源了。

為什么IoU較大，認為是線性變換？

當輸入的 Proposal 與 Ground Truth 相差較小時(RCNN 設置的是 IoU>0.6)，可以認為這種變換是一種線性變換，那么我們就可以用線性回歸來建模對窗口進行微調，否則會導致訓練的回歸模型不 work（當 Proposal跟 GT 離得較遠，就是復雜的非線性問題了，此時用線性回歸建模顯然不合理）。這里我來解釋：

Log函數明顯不滿足線性函數，但是為什么當Proposal 和Ground Truth相差較小的時候，就可以認為是一種線性變換呢？大家還記得這個公式不？參看高數1。

$lim_{x = 0}log(1 + x) = x$

現在回過來看公式(8):

$tw=log??(Gw/Pw)=log(Gw+Pw?PwPw)=log(1+Gw?PwPw)t_{w} = \log ?(G_{w}/ P_{w}) = log(\frac{G_{w} + P_{w}?P_{w}}{P_{w}}) = log(1 + \frac{G_{w}?P_{w}}{P_{w}})$