Johnson 全源最短路徑算法

解決單源最短路徑問題（Single Source Shortest Paths Problem）的算法包括：

Dijkstra 單源最短路徑算法：時間復雜度為 O(E + VlogV)，要求權值非負；
Bellman-Ford 單源最短路徑算法：時間復雜度為 O(VE)，適用于帶負權值情況；

對于全源最短路徑問題（All-Pairs Shortest Paths Problem），可以認為是單源最短路徑問題的推廣，即分別以每個頂點作為源頂點并求其至其它頂點的最短距離。例如，對每個頂點應用?Bellman-Ford 算法，則可得到所有頂點間的最短路徑的運行時間為?O(V²E)，由于圖中頂點都是連通的，而邊的數量可能會比頂點更多，這個時間沒有比?Floyd-Warshall?全源最短路徑算法?O(V³) 更優。那么，再試下對每個頂點應用?Dijkstra 算法，則可得到所有頂點間的最短路徑的運行時間為?O(VE + V²logV)，看起來優于 Floyd-Warshall 算法的 O(V³)，所以看起來使用基于?Dijkstra 算法的改進方案好像更好，但問題是?Dijkstra 算法要求圖中所有邊的權值非負，不適合通用的情況。

在 1977 年，Donald B. Johnson?提出了對所有邊的權值進行 "re-weight" 的算法，使得邊的權值非負，進而可以使用?Dijkstra 算法進行最短路徑的計算。

我們先自己思考下如何進行?"re-weight" 操作，比如，簡單地對每條邊的權值加上一個較大的正數，使其非負，是否可行？

   1     1     1
s-----a-----b-----c\              /\          /\______/4

比如上面的圖中，共 4 條邊，權值分別為 1,1,1,4。當前 s --> c 的最短路徑是 {s-a, a-b, b-c} 即 1+1+1=3。而如果將所有邊的權值加 1，則最短路徑就會變成 {s-c} 的 5，因為 2+2+2=6，實際上導致了最短路徑的變化，顯然是錯誤的。

那么，Johnson 算法是如何對邊的權值進行?"re-weight" 的呢？以下面的圖 G 為例，有 4 個頂點和 5 條邊。

首先，新增一個源頂點 4，并使其與所有頂點連通，新邊賦權值為 0，如下圖所示。

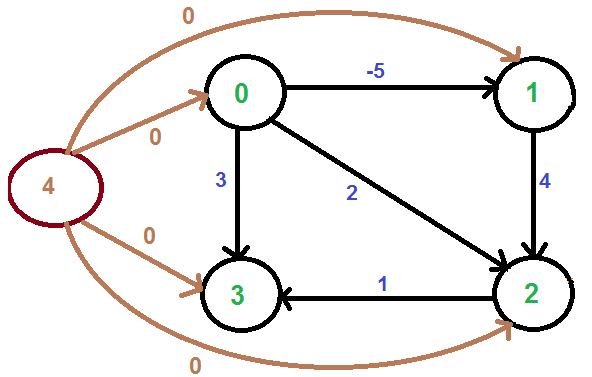
使用?Bellman-Ford 算法?計算新的頂點到所有其它頂點的最短路徑，則從 4 至 {0, 1, 2, 3} 的最短路徑分別是 {0, -5, -1, 0}。即有 h[] =?{0, -5, -1, 0}。當得到這個 h[] 信息后，將新增的頂點 4 移除，然后使用如下公式對所有邊的權值進行 "re-weight"：

w(u, v) = w(u, v) + (h[u] - h[v]).

則可得到下圖中的結果：

此時，所有邊的權值已經被 "re-weight" 為非負。此時，就可以利用?Dijkstra 算法對每個頂點分別進行最短路徑的計算了。

Johnson 算法描述如下：

給定圖 G = (V, E)，增加一個新的頂點 s，使 s 指向圖 G 中的所有頂點都建立連接，設新的圖為 G’；
對圖 G’ 中頂點 s?使用?Bellman-Ford 算法計算單源最短路徑，得到結果 h[] = {h[0], h[1], .. h[V-1]}；
對原圖 G 中的所有邊進行 "re-weight"，即對于每個邊 (u, v)，其新的權值為?w(u, v) + (h[u] - h[v])；
移除新增的頂點 s，對每個頂點運行?Dijkstra 算法求得最短路徑；

Johnson 算法的運行時間為?O(V²logV + VE)。

Johnson 算法偽碼實現如下：

Johnson 算法?C# 代碼實現如下：

  1 using System;
  2 using System.Collections.Generic;
  3 using System.Linq;
  4 
  5 namespace GraphAlgorithmTesting
  6 {
  7   class Program
  8   {
  9     static void Main(string[] args)
 10     {
 11       // build a directed and negative weighted graph
 12       Graph directedGraph1 = new Graph(5);
 13       directedGraph1.AddEdge(0, 1, -1);
 14       directedGraph1.AddEdge(0, 2, 4);
 15       directedGraph1.AddEdge(1, 2, 3);
 16       directedGraph1.AddEdge(1, 3, 2);
 17       directedGraph1.AddEdge(1, 4, 2);
 18       directedGraph1.AddEdge(3, 2, 5);
 19       directedGraph1.AddEdge(3, 1, 1);
 20       directedGraph1.AddEdge(4, 3, -3);
 21 
 22       Console.WriteLine();
 23       Console.WriteLine("Graph Vertex Count : {0}", directedGraph1.VertexCount);
 24       Console.WriteLine("Graph Edge Count : {0}", directedGraph1.EdgeCount);
 25       Console.WriteLine();
 26 
 27       int[,] distSet1 = directedGraph1.Johnsons();
 28       PrintSolution(directedGraph1, distSet1);
 29 
 30       // build a directed and positive weighted graph
 31       Graph directedGraph2 = new Graph(4);
 32       directedGraph2.AddEdge(0, 1, 5);
 33       directedGraph2.AddEdge(0, 3, 10);
 34       directedGraph2.AddEdge(1, 2, 3);
 35       directedGraph2.AddEdge(2, 3, 1);
 36 
 37       Console.WriteLine();
 38       Console.WriteLine("Graph Vertex Count : {0}", directedGraph2.VertexCount);
 39       Console.WriteLine("Graph Edge Count : {0}", directedGraph2.EdgeCount);
 40       Console.WriteLine();
 41 
 42       int[,] distSet2 = directedGraph2.Johnsons();
 43       PrintSolution(directedGraph2, distSet2);
 44 
 45       Console.ReadKey();
 46     }
 47 
 48     private static void PrintSolution(Graph g, int[,] distSet)
 49     {
 50       Console.Write("\t");
 51       for (int i = 0; i < g.VertexCount; i++)
 52       {
 53         Console.Write(i + "\t");
 54       }
 55       Console.WriteLine();
 56       Console.Write("\t");
 57       for (int i = 0; i < g.VertexCount; i++)
 58       {
 59         Console.Write("-" + "\t");
 60       }
 61       Console.WriteLine();
 62       for (int i = 0; i < g.VertexCount; i++)
 63       {
 64         Console.Write(i + "|\t");
 65         for (int j = 0; j < g.VertexCount; j++)
 66         {
 67           if (distSet[i, j] == int.MaxValue)
 68           {
 69             Console.Write("INF" + "\t");
 70           }
 71           else
 72           {
 73             Console.Write(distSet[i, j] + "\t");
 74           }
 75         }
 76         Console.WriteLine();
 77       }
 78     }
 79 
 80     class Edge
 81     {
 82       public Edge(int begin, int end, int weight)
 83       {
 84         this.Begin = begin;
 85         this.End = end;
 86         this.Weight = weight;
 87       }
 88 
 89       public int Begin { get; private set; }
 90       public int End { get; private set; }
 91       public int Weight { get; private set; }
 92 
 93       public void Reweight(int newWeight)
 94       {
 95         this.Weight = newWeight;
 96       }
 97 
 98       public override string ToString()
 99       {
100         return string.Format(
101           "Begin[{0}], End[{1}], Weight[{2}]",
102           Begin, End, Weight);
103       }
104     }
105 
106     class Graph
107     {
108       private Dictionary<int, List<Edge>> _adjacentEdges
109         = new Dictionary<int, List<Edge>>();
110 
111       public Graph(int vertexCount)
112       {
113         this.VertexCount = vertexCount;
114       }
115 
116       public int VertexCount { get; private set; }
117 
118       public int EdgeCount
119       {
120         get
121         {
122           return _adjacentEdges.Values.SelectMany(e => e).Count();
123         }
124       }
125 
126       public void AddEdge(int begin, int end, int weight)
127       {
128         if (!_adjacentEdges.ContainsKey(begin))
129         {
130           var edges = new List<Edge>();
131           _adjacentEdges.Add(begin, edges);
132         }
133 
134         _adjacentEdges[begin].Add(new Edge(begin, end, weight));
135       }
136 
137       public void AddEdge(Edge edge)
138       {
139         AddEdge(edge.Begin, edge.End, edge.Weight);
140       }
141 
142       public void AddEdges(IEnumerable<Edge> edges)
143       {
144         foreach (var edge in edges)
145         {
146           AddEdge(edge);
147         }
148       }
149 
150       public IEnumerable<Edge> GetAllEdges()
151       {
152         return _adjacentEdges.Values.SelectMany(e => e);
153       }
154 
155       public int[,] Johnsons()
156       {
157         // distSet[,] will be the output matrix that will finally have the shortest 
158         // distances between every pair of vertices
159         int[,] distSet = new int[VertexCount, VertexCount];
160 
161         for (int i = 0; i < VertexCount; i++)
162         {
163           for (int j = 0; j < VertexCount; j++)
164           {
165             distSet[i, j] = int.MaxValue;
166           }
167         }
168         for (int i = 0; i < VertexCount; i++)
169         {
170           distSet[i, i] = 0;
171         }
172 
173         // step 1: add new vertex s and connect to all vertices
174         Graph g = new Graph(this.VertexCount + 1);
175         g.AddEdges(this.GetAllEdges());
176 
177         int s = this.VertexCount;
178         for (int i = 0; i < this.VertexCount; i++)
179         {
180           g.AddEdge(s, i, 0);
181         }
182 
183         // step 2: use Bellman-Ford to evaluate shortest paths from s
184         int[] h = g.BellmanFord(s);
185 
186         // step 3: re-weighting edges of the original graph
187         //         w(u, v) = w(u, v) + (h[u] - h[v])
188         foreach (var edge in this.GetAllEdges())
189         {
190           edge.Reweight(edge.Weight + (h[edge.Begin] - h[edge.End]));
191         }
192 
193         // step 4: use Dijkstra for each edges
194         for (int begin = 0; begin < this.VertexCount; begin++)
195         {
196           int[] dist = this.Dijkstra(begin);
197           for (int end = 0; end < dist.Length; end++)
198           {
199             if (dist[end] != int.MaxValue)
200             {
201               distSet[begin, end] = dist[end] - (h[begin] - h[end]);
202             }
203           }
204         }
205 
206         return distSet;
207       }
208 
209       public int[,] FloydWarshell()
210       {
211         /* distSet[,] will be the output matrix that will finally have the shortest 
212            distances between every pair of vertices */
213         int[,] distSet = new int[VertexCount, VertexCount];
214 
215         for (int i = 0; i < VertexCount; i++)
216         {
217           for (int j = 0; j < VertexCount; j++)
218           {
219             distSet[i, j] = int.MaxValue;
220           }
221         }
222         for (int i = 0; i < VertexCount; i++)
223         {
224           distSet[i, i] = 0;
225         }
226 
227         /* Initialize the solution matrix same as input graph matrix. Or 
228            we can say the initial values of shortest distances are based
229            on shortest paths considering no intermediate vertex. */
230         foreach (var edge in _adjacentEdges.Values.SelectMany(e => e))
231         {
232           distSet[edge.Begin, edge.End] = edge.Weight;
233         }
234 
235         /* Add all vertices one by one to the set of intermediate vertices.
236           ---> Before start of a iteration, we have shortest distances between all
237           pairs of vertices such that the shortest distances consider only the
238           vertices in set {0, 1, 2, .. k-1} as intermediate vertices.
239           ---> After the end of a iteration, vertex no. k is added to the set of
240           intermediate vertices and the set becomes {0, 1, 2, .. k} */
241         for (int k = 0; k < VertexCount; k++)
242         {
243           // Pick all vertices as source one by one
244           for (int i = 0; i < VertexCount; i++)
245           {
246             // Pick all vertices as destination for the above picked source
247             for (int j = 0; j < VertexCount; j++)
248             {
249               // If vertex k is on the shortest path from
250               // i to j, then update the value of distSet[i,j]
251               if (distSet[i, k] != int.MaxValue
252                 && distSet[k, j] != int.MaxValue
253                 && distSet[i, k] + distSet[k, j] < distSet[i, j])
254               {
255                 distSet[i, j] = distSet[i, k] + distSet[k, j];
256               }
257             }
258           }
259         }
260 
261         return distSet;
262       }
263 
264       public int[] BellmanFord(int source)
265       {
266         // distSet[i] will hold the shortest distance from source to i
267         int[] distSet = new int[VertexCount];
268 
269         // Step 1: Initialize distances from source to all other vertices as INFINITE
270         for (int i = 0; i < VertexCount; i++)
271         {
272           distSet[i] = int.MaxValue;
273         }
274         distSet[source] = 0;
275 
276         // Step 2: Relax all edges |V| - 1 times. A simple shortest path from source
277         // to any other vertex can have at-most |V| - 1 edges
278         for (int i = 1; i <= VertexCount - 1; i++)
279         {
280           foreach (var edge in _adjacentEdges.Values.SelectMany(e => e))
281           {
282             int u = edge.Begin;
283             int v = edge.End;
284             int weight = edge.Weight;
285 
286             if (distSet[u] != int.MaxValue
287               && distSet[u] + weight < distSet[v])
288             {
289               distSet[v] = distSet[u] + weight;
290             }
291           }
292         }
293 
294         // Step 3: check for negative-weight cycles.  The above step guarantees
295         // shortest distances if graph doesn't contain negative weight cycle.
296         // If we get a shorter path, then there is a cycle.
297         foreach (var edge in _adjacentEdges.Values.SelectMany(e => e))
298         {
299           int u = edge.Begin;
300           int v = edge.End;
301           int weight = edge.Weight;
302 
303           if (distSet[u] != int.MaxValue
304             && distSet[u] + weight < distSet[v])
305           {
306             Console.WriteLine("Graph contains negative weight cycle.");
307           }
308         }
309 
310         return distSet;
311       }
312 
313       public int[] Dijkstra(int source)
314       {
315         // dist[i] will hold the shortest distance from source to i
316         int[] distSet = new int[VertexCount];
317 
318         // sptSet[i] will true if vertex i is included in shortest
319         // path tree or shortest distance from source to i is finalized
320         bool[] sptSet = new bool[VertexCount];
321 
322         // initialize all distances as INFINITE and stpSet[] as false
323         for (int i = 0; i < VertexCount; i++)
324         {
325           distSet[i] = int.MaxValue;
326           sptSet[i] = false;
327         }
328 
329         // distance of source vertex from itself is always 0
330         distSet[source] = 0;
331 
332         // find shortest path for all vertices
333         for (int i = 0; i < VertexCount - 1; i++)
334         {
335           // pick the minimum distance vertex from the set of vertices not
336           // yet processed. u is always equal to source in first iteration.
337           int u = CalculateMinDistance(distSet, sptSet);
338 
339           // mark the picked vertex as processed
340           sptSet[u] = true;
341 
342           // update dist value of the adjacent vertices of the picked vertex.
343           for (int v = 0; v < VertexCount; v++)
344           {
345             // update dist[v] only if is not in sptSet, there is an edge from 
346             // u to v, and total weight of path from source to  v through u is 
347             // smaller than current value of dist[v]
348             if (!sptSet[v]
349               && distSet[u] != int.MaxValue
350               && _adjacentEdges.ContainsKey(u)
351               && _adjacentEdges[u].Exists(e => e.End == v))
352             {
353               int d = _adjacentEdges[u].Single(e => e.End == v).Weight;
354               if (distSet[u] + d < distSet[v])
355               {
356                 distSet[v] = distSet[u] + d;
357               }
358             }
359           }
360         }
361 
362         return distSet;
363       }
364 
365       private int CalculateMinDistance(int[] distSet, bool[] sptSet)
366       {
367         int minDistance = int.MaxValue;
368         int minDistanceIndex = -1;
369 
370         for (int v = 0; v < VertexCount; v++)
371         {
372           if (!sptSet[v] && distSet[v] <= minDistance)
373           {
374             minDistance = distSet[v];
375             minDistanceIndex = v;
376           }
377         }
378 
379         return minDistanceIndex;
380       }
381     }
382   }
383 }