目錄

摘要

一、概述

二、SVM算法定義

1.超平?最?間隔介紹

2.硬間隔和軟間隔

1.硬間隔分類

2.?軟間隔分類

三、SVM算法原理

1 定義輸?數據

2 線性可分?持向量機

3 SVM的計算過程與算法步驟

四、核函數

五、SVM算法api介紹

1. 核心參數說明

2. 主要方法

3. 重要屬性

六、SVM支持向量機的優缺點

1、優點

2、缺點

---

摘要

支持向量機(SVM)是一種監督學習算法,用于數據的二元分類。它通過尋找最大邊距超平面實現分類,適用于小樣本和非線性問題。SVM能夠處理線性和非線性數據,通過核函數將低維不可分數據映射到高維空間,實現線性可分。本文介紹了SVM的基本原理、硬間隔和軟間隔概念、核函數以及模型評估方法。

一、概述

支持向量機（SVM）是一類按監督學習方式對數據進行二元分類的廣義線性分類器，其決策邊界是對學習樣本求解的最大邊距超平面，可以將問題化為一個求解凸二次規劃的問題。與邏輯回歸和神經網絡相比，支持向量機，在學習復雜的非線性方程時提供了一種更為清晰，更加強大的方式。

具體來說：在線性可分時，在原空間尋找兩類樣本的最優分類超平面。在線性不可分時，加入松弛變量并通過使用非線性映射將低維度輸入空間的樣本映射到高維度空間使其變為線性可分，這樣就可以在該特征空間中尋找最優分類超平面。

SVM使用準則： n為特征數， m為訓練樣本數。

如果相較于m而言，n要大許多，即訓練集數據量不夠支持我們訓練一個復雜的非線性模型，我們選用邏輯回歸模型或者不帶核函數的支持向量機。
如果?n較小，而且 m 大小中等，例如 n 在 1-1000 之間，而 m 在10-10000之間，使用高斯核函數的支持向量機。
如果 n 較小，而 m 較大，例如 n 在1-1000之間，而 m 大于50000，則使用支持向量機會非常慢，解決方案是創造、增加更多的特征，然后使用邏輯回歸或不帶核函數的支持向量機。

二、SVM算法定義

SVM：SVM全稱是supported vector machine（?持向量機），即尋找到?個超平?使樣本分成兩類，并且間隔最 ?。 SVM能夠執?線性或?線性分類、回歸，甚?是異常值檢測任務。它是機器學習領域最受歡迎的模型之?。SVM特別 適?于中?型復雜數據集的分類。

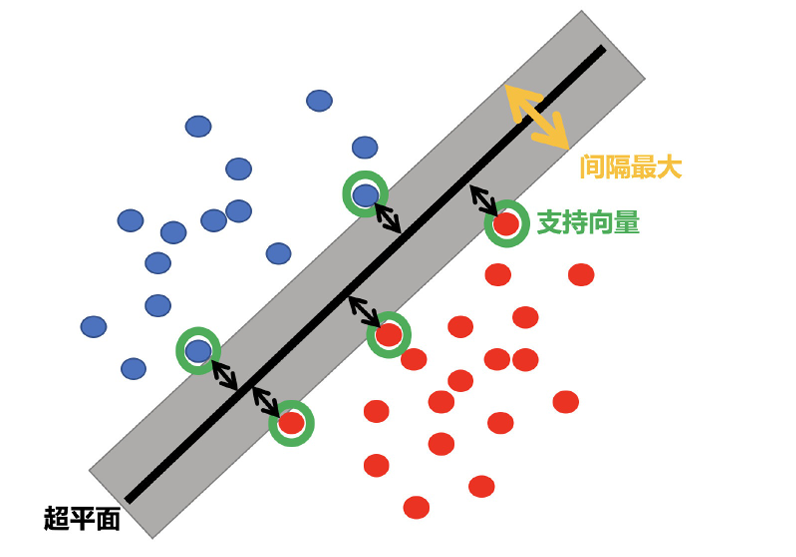
1.超平?最?間隔介紹

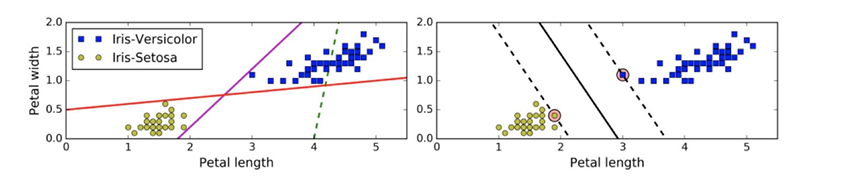上左圖顯示了三種可能的線性分類器的決策邊界：

虛線所代表的模型表現?常糟糕，甚?都?法正確實現分類。其余兩個模型在這個訓練集上表現堪稱完美，但是它們的 決策邊界與實例過于接近，導致在?對新實例時，表現可能不會太好

右圖中的實線代表SVM分類器的決策邊界，不僅分離了兩個類別，且盡可能遠離最近的訓練實例。

2.硬間隔和軟間隔

1.硬間隔分類

在上?我們使?超平?進?分割數據的過程中，如果我們嚴格地讓所有實例都不在最?間隔之間，并且位于正確的? 邊，這就是硬間隔分類。 硬間隔分類有兩個問題，?先，它只在數據是線性可分離的時候才有效；其次，它對異常值?常敏感。 當有?個額外異常值的鳶尾花數據：左圖的數據根本找不出硬間隔，?右圖最終顯示的決策邊界與我們之前所看到的? 異常值時的決策邊界也?不相同，可能?法很好地泛化

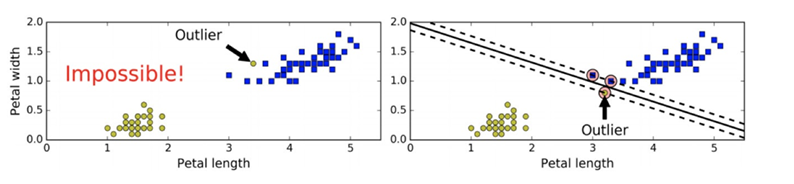
2.?軟間隔分類

要避免這些問題，最好使?更靈活的模型。?標是盡可能在保持最?間隔寬闊和限制間隔違例（即位于最?間隔之上， 甚?在錯誤的?邊的實例）之間找到良好的平衡，這就是軟間隔分類。 要避免這些問題，最好使?更靈活的模型。?標是盡可能在保持間隔寬闊和限制間隔違例之間找到良好的平衡，這就是 軟間隔分類

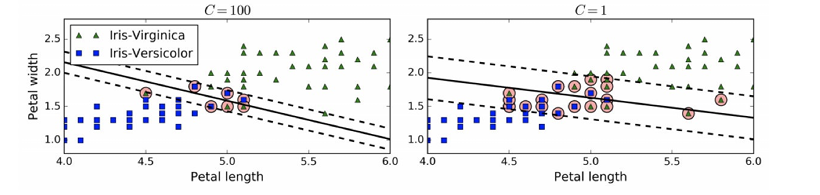
在Scikit-Learn的SVM類中，可以通過超參數C來控制這個平衡：C值越?，則間隔越寬，但是間隔違例也會越多。上圖 顯示了在?個?線性可分離數據集上，兩個軟間隔SVM分類器各?的決策邊界和間隔。

左邊使?了?C值，分類器的錯誤樣本（間隔違例）較少，但是間隔也較?。

右邊使?了低C值，間隔?了很多，但是位于間隔上的實例也更多。

看起來第?個分類器的泛化效果更好，因為?多數 間隔違例實際上都位于決策邊界正確的?邊，所以即便是在該訓練集上，它做出的錯誤預測也會更少。

三、SVM算法原理

1 定義輸?數據

假設給定?個特征空間上的訓練集為：

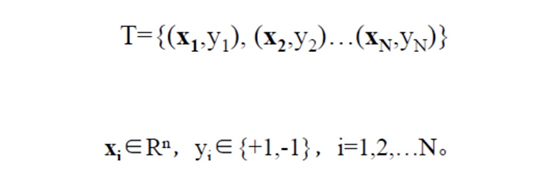
其中，(xi,yi )稱為樣本點。

xi 為第i個實例（樣本）， yi 為xi的標記：當yi =1時，xi為正例 當yi =?1時，xi為負例?

2 線性可分?持向量機

給定了上?提出的線性可分訓練數據集，通過間隔最?化得到分離超平?為 :y(x)=wT Φ(x)+b?T 相應的分類決策函數為： f(x)=sign(wT Φ(x)+b) 以上決策函數就稱為線性可分?持向量機。

這?解釋?下Φ(x)這個東東。 i這是某個確定的特征空間轉換函數，它的作?是將x映射到更?的維度，它有?個以后我們經常會?到的專有稱號”核函 數“。

以上就是線性可分?持向量機的模型表達式。我們要去求出這樣?個模型，或者說這樣?個超平?y(x),它能夠最優地分 離兩個集合。 其實也就是我們要去求?組參數（w,b),使其構建的超平?函數能夠最優地分離兩個集合。 如下就是?個最優超平?:

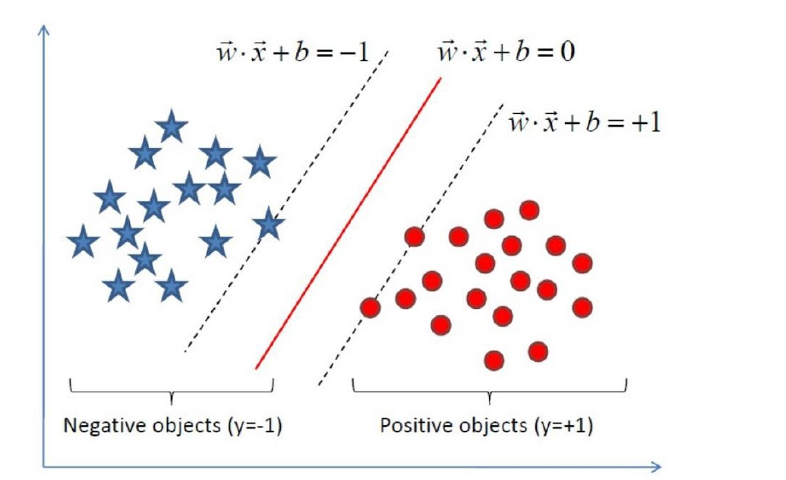
3 SVM的計算過程與算法步驟

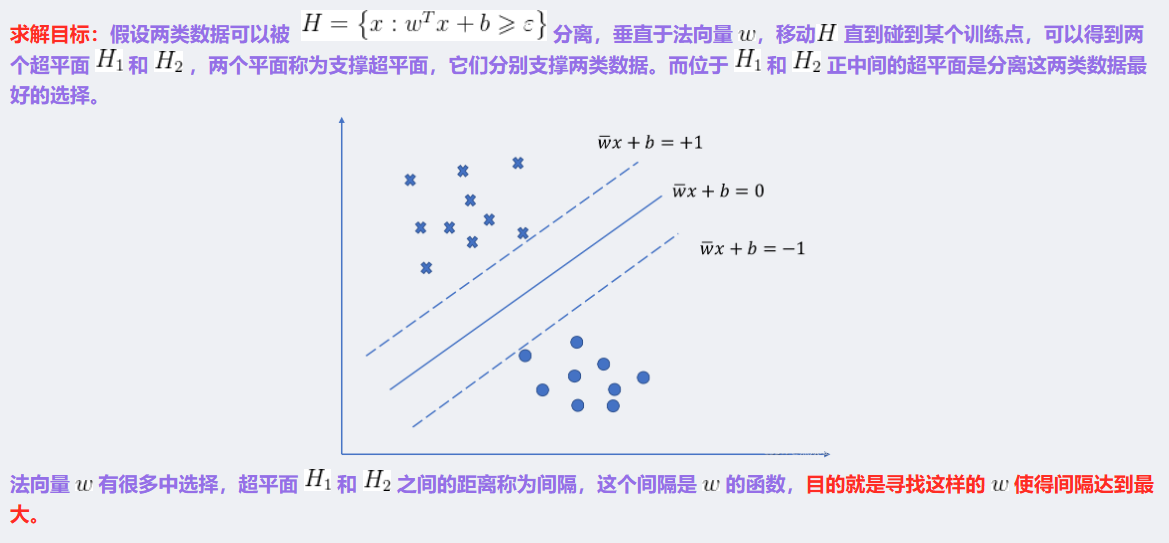
對偶問題

四、核函數

支持向量機算法分類和回歸方法的中都支持線性性和非線性類型的數據類型。非線性類型通常是二維平面不可分，為了使數據可分，需要通過一個函數將原始數據映射到高維空間，從而使得數據在高維空間很容易可分，需要通過一個函數將原始數據映射到高維空間，從而使得數據在高維空間很容易區分，這樣就達到數據分類或回歸的目的，而實現這一目標的函數稱為核函數。

工作原理：當低維空間內線性不可分時，可以通過高位空間實現線性可分。但如果在高維空間內直接進行分類或回歸時，則存在確定非線性映射函數的形式和參數問題，而最大的障礙就是高維空間的運算困難且結果不理想。通過核函數的方法，可以將高維空間內的點積運算，巧妙轉化為低維輸入空間內核函數的運算，從而有效解決這一問題。

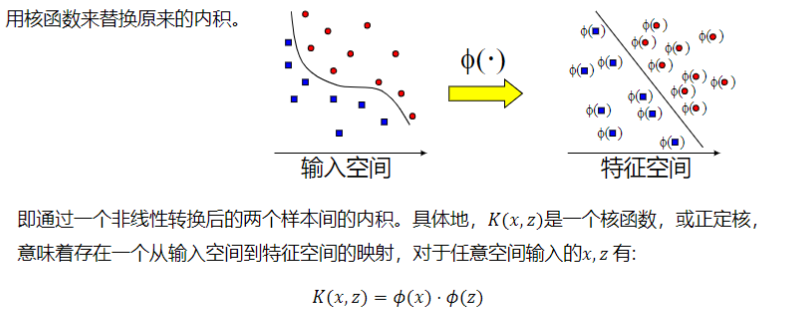
常見的核函數：

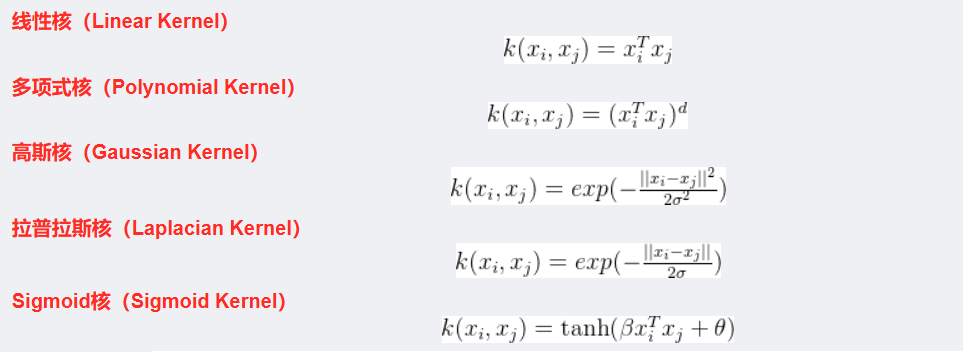
五、SVM算法api介紹

SVC(kernel='rbf', C=1.0, gamma='scale', degree=3, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)

• 1. 核心參數說明

• kernel：核函數類型，決定數據映射到高維空間的方式

  'linear'：線性核（默認用于線性可分數據）
• 'rbf'：徑向基函數（默認值，適用于非線性數據，需配合gamma調整）
• 'poly'：多項式核（參數degree控制階數）
• 'sigmoid'：Sigmoid 核

• C：正則化參數（默認 1.0）

  控制對誤分類的懲罰程度，C越大，模型對訓練集擬合越嚴格（可能過擬合）；C越小，容錯性越強（可能欠擬合）。

• gamma：核系數（僅對rbf、poly、sigmoid有效）

  'scale'（默認）：1/(n_features * X.var())
• 'auto'：1/n_features
• 數值越大，核函數作用范圍越小（可能過擬合）；反之則作用范圍廣（可能欠擬合）。

• degree：多項式核的階數（默認 3），僅當kernel='poly'時有效。

• class_weight：類別權重（用于不平衡數據）

  None（默認）：所有類別權重相同
• 'balanced'：根據訓練樣本比例自動計算權重（n_samples / (n_classes * np.bincount(y))）

2. 主要方法

• fit(X, y)：訓練模型

  X：特征數據（形狀為[n_samples, n_features]）
• y：標簽數據（形狀為[n_samples]）

• predict(X)：預測新樣本類別

  返回預測標簽數組（形狀為[n_samples]）

• predict_proba(X)：預測每個類別的概率（需設置probability=True）

  返回概率矩陣（形狀為[n_samples, n_classes]）

• score(X, y)：計算模型在X和y上的準確率（accuracy）

• decision_function(X)：返回樣本到決策邊界的距離（用于獲取支持向量等）

3. 重要屬性

• support_vectors_：訓練集中的支持向量
• coef_：線性核的權重系數（僅當kernel='linear'時有效）
• intercept_：線性核的偏置項
• n_support_：每個類別的支持向量數量

六、SVM支持向量機的優缺點

1、優點

1. 良好的泛化能力
   SVM 的核心思想是尋找 “最大間隔超平面”，通過最大化類別間的間隔，使模型對未知數據具有較強的泛化能力，尤其在小樣本數據集上表現出色。

2. 適用于高維空間
   即使特征維度高于樣本數量，SVM 仍能有效工作（例如文本分類中，特征維度常遠大于樣本數），因為它無需依賴數據的維度規模，而是通過核函數處理高維映射。

3. 通過核函數處理非線性問題
   借助核函數（如 RBF、多項式核等），SVM 可以將低維非線性可分的數據映射到高維空間，轉化為線性可分問題，靈活處理非線性分類任務。

4. 對噪聲不敏感（一定程度上）
   通過引入正則化參數C，SVM 可以控制對噪聲的容忍度，平衡間隔最大化和分類錯誤最小化，避免過度擬合噪聲數據。

5. 決策邊界清晰
   最終的決策邊界僅由支持向量決定，無需依賴全部樣本，計算復雜度不隨樣本數量激增而大幅上升（尤其在核函數為線性時）。

2、缺點

1. 對大規模數據集效率較低
   SVM 的訓練過程涉及求解凸二次規劃問題，時間復雜度較高（通常為O(n3)，n為樣本數），在百萬級以上樣本的數據集上訓練速度較慢。

2. 對參數和核函數選擇敏感
   模型性能高度依賴于核函數類型（如線性核、RBF 核）和參數（如C、核函數參數γ）的選擇，需要通過交叉驗證等方法調參，過程較繁瑣。

3. 不適用于多類別問題（原生支持二分類）
   SVM 原生僅支持二分類任務，處理多類別問題時需通過 “一對多”（One-vs-Rest）或 “一對一”（One-vs-One）等策略轉換，增加了計算復雜度。

4. 對缺失數據敏感
   SVM 假設數據是完整的，對缺失值較為敏感，需要先對數據進行預處理（如填充缺失值），否則會影響模型性能。

5. 結果解釋性較差
   與決策樹等模型不同，SVM 的決策邊界由支持向量和核函數共同決定，難以直觀解釋特征對分類結果的影響，缺乏可解釋性。