原標題：蒙特·卡羅方法中的數學之美，你一定不想錯過

有方教育——我們致力于為中學生提供學界和業界前沿的學術科研教育內容，幫助學生參加海外科研項目，在提升申請競爭力的同時，獲得領跑優勢。

一、概述

蒙特·卡羅方法(Monte Carlo method)，也稱統計模擬方法，是二十世紀四十年代中期由于科學技術的發展和電子計算機的發明，而被提出的一種以概率統計理論為指導的一類非常重要的數值計算方法。是指使用隨機數(或更常見的偽隨機數)來解決很多計算問題的方法。與它對應的是確定性算法。蒙特·卡羅方法在金融工程學，宏觀經濟學，計算物理學(如粒子輸運計算、量子熱力學計算、空氣動力學計算)等領域應用廣泛。

它誕生于上個世紀40年代美國的”曼哈頓計劃”，名字來源于賭城蒙特卡羅，象征概率。

當所求解問題是某種隨機事件出現的概率，或者是某個隨機變量的期望值時，通過某種“實驗”的方法，以這種事件出現的頻率估計這一隨機事件的概率，或者得到這個隨機變量的某些數字特征，并將其作為問題的解。、

蒙特卡羅方法的解題過程可以歸結為三個主要步驟：構造或描述概率過程；實現從已知概率分布抽樣；建立各種估計量。

蒙特卡羅方法解題過程的三個主要步驟：

(1)構造或描述概率過程

對于本身就具有隨機性質的問題，如粒子輸運問題，主要是正確描述和模擬這個概率過 程，對于本來不是隨機性質的確定性問題，比如計算定積分，就必須事先構造一個人為的概率過程，它的某些參量正好是所要求問題的解。即要將不具有隨機性質的問題轉化為隨機性質的問題。

(2)實現從已知概率分布抽樣

構造了概率模型以后，由于各種概率模型都可以看作是由各種各樣的概率分布構成的，因此產生已知概率分布的隨機變量(或隨機向量)，就成為實現蒙特卡羅方法模擬實驗的基本手段，這也是蒙特卡羅方法被稱為隨機抽樣的原因。最簡單、最基本、最重要的一個概率分布是(0，1)上的均勻分布(或稱矩形分布)。隨機數就是具有這種均勻分布的隨機變量。隨機數序列就是具有這種分布的總體的一個簡單子樣，也就是一個具有這種分布的相互獨立的隨機變數序列。產生隨機數的問題，就是從這個分布的抽樣問題。在計算機上，可以用物理方法產生隨機數，但價格昂貴，不能重復，使用不便。另一種方法是用數學遞推公式產生。這樣產生的序列，與真正的隨機數序列不同，所以稱為偽隨機數，或偽隨機數序列。不過，經過多種統計檢驗表明，它與真正的隨機數，或隨機數序列具有相近的性質，因此可把它作為真正的隨機數來使用。由已知分布隨機抽樣有各種方法，與從(0,1)上均勻分布抽樣不同，這些方法都是借助于隨機序列來實現的，也就是說，都是以產生隨機數為前提的。由此可見，隨機數是我們實現蒙特卡羅模擬的基本工具。

(3)建立各種估計量

一般說來，構造了概率模型并能從中抽樣后，即實現模擬實驗后，我們就要確定一個隨機變量，作為所要求的問題的解，我們稱它為無偏估計。建立各種估計量，相當于對模擬實驗的結果進行考察和登記，從中得到問題的解。

數學應用：

通常蒙特·卡羅方法通過構造符合一定規則的隨機數來解決數學上的各種問題。對于那些由于計算過于復雜而難以得到解析解或者根本沒有解析解的問題，蒙特·卡羅方法是一種有效的求出數值解的方法。一般蒙特·卡羅方法在數學中最常見的應用就是蒙特·卡羅積分。

從理論上來說，蒙特卡羅方法需要大量的實驗。實驗次數越多，所得到的結果才越精確。

計算機技術的發展，使得蒙特卡羅方法在最近10年得到快速的普及。現代的蒙特卡羅方法，已經不必親自動手做實驗，而是借助計算機的高速運轉能力，使得原本費時費力的實驗過程，變成了快速和輕而易舉的事情。它不但用于解決許多復雜的科學方面的問題，也被項目管理人員經常使用。

借助計算機技術，蒙特卡羅方法實現了兩大優點：

一是簡單，省卻了繁復的數學推導和演算過程，使得一般人也能夠理解和掌握

二是快速。簡單和快速，是蒙特卡羅方法在現代項目管理中獲得應用的技術基礎。

蒙特卡羅方法有很強的適應性，問題的幾何形狀的復雜性對它的影響不大。該方法的收斂性是指概率意義下的收斂，因此問題維數的增加不會影響它的收斂速度，而且存貯單元也很省，這些是用該方法處理大型復雜問題時的優勢。因此，隨著電子計算機的發展和科學技術問題的日趨復雜，蒙特卡羅方法的應用也越來越廣泛。它不僅較好地解決了多重積分計算、微分方程求解、積分方程求解、特征值計算和非線性方程組求解等高難度和復雜的數學計算問題，而且在統計物理、核物理、真空技術、系統科學 、信息科學、公用事業、地質、醫學，可靠性及計算機科學等廣泛的領域都得到成功的應用。

接下來列舉幾個蒙特·卡羅方法的應用實例。

二、π的計算

第一個例子是，如何用蒙特卡羅方法計算圓周率π。

正方形內部有一個相切的圓，它們的面積之比是π/4。

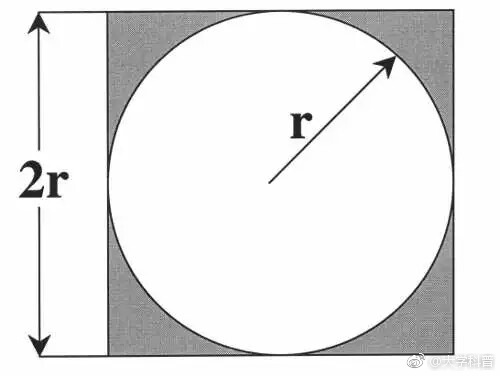
現在，在這個正方形內部，隨機產生10000個點(即10000個坐標對 (x, y))，計算它們與中心點的距離，從而判斷是否落在圓的內部。

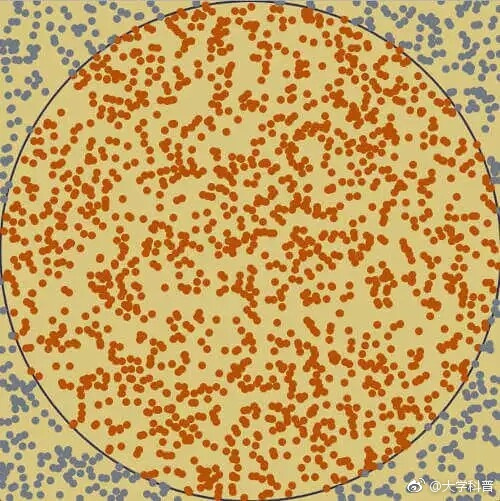
如果這些點均勻分布，那么圓內的點應該占到所有點的 π/4，因此將這個比值乘以4，就是π的值。通過R語言腳本隨機模擬30000個點，π的估算值與真實值相差0.07%。

一直到公元20世紀初期，盡管實驗次數數以千計，利用蒙特卡羅方法所得到的圓周率π值，還是達不到公元5世紀祖沖之的推算精度。這可能是傳統蒙特卡羅方法長期得不到推廣的主要原因。

三、積分的計算

上面的方法加以推廣，就可以計算任意一個積分的值。

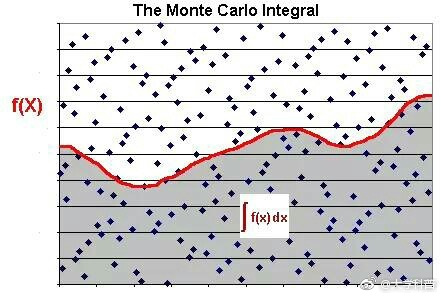
比如，計算函數 y = x2 在 [0, 1] 區間的積分，就是求出下圖紅色部分的面積。

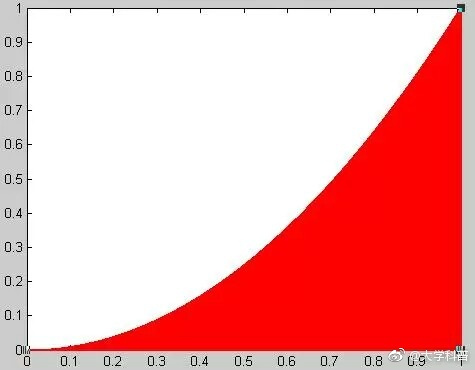
這個函數在 (1,1) 點的取值為1，所以整個紅色區域在一個面積為1的正方形里面。在該正方形內部，產生大量隨機點，可以計算出有多少點落在紅色區域(判斷條件 y < x2)。這個比重就是所要求的積分值。

用Matlab模擬100萬個隨機點，結果為0.3328。

四、交通堵塞

蒙特卡羅方法不僅可以用于計算，還可以用于模擬系統內部的隨機運動。下面的例子模擬單車道的交通堵塞。

根據 Nagel-Schreckenberg 模型，車輛的運動滿足以下規則。

當前速度是 v 。

如果前面沒車，它在下一秒的速度會提高到 v + 1 ，直到達到規定的最高限速。

如果前面有車，距離為d，且 d < v，那么它在下一秒的速度會降低到 d – 1 。

此外，司機還會以概率 p 隨機減速， 將下一秒的速度降低到 v – 1 。

在一條直線上，隨機產生100個點，代表道路上的100輛車，另取概率 p 為 0.3 。

上圖中，橫軸代表距離(從左到右)，縱軸代表時間(從上到下)，因此每一行就表示下一秒的道路情況。

可以看到，該模型會隨機產生交通擁堵(圖形上黑色聚集的部分)。這就證明了，單車道即使沒有任何原因，也會產生交通堵塞。

五、產品厚度

某產品由八個零件堆疊組成。也就是說，這八個零件的厚度總和，等于該產品的厚度。

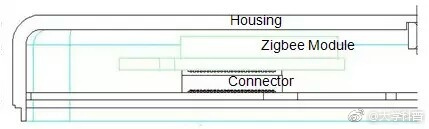
已知該產品的厚度，必須控制在27mm以內，但是每個零件有一定的概率，厚度會超出誤差。請問有多大的概率，產品的厚度會超出27mm？

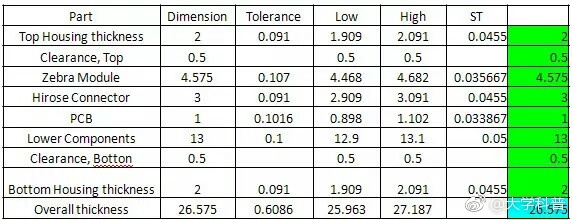
取100000個隨機樣本，每個樣本有8個值，對應8個零件各自的厚度。計算發現，產品的合格率為99.9979%，即百萬分之21的概率，厚度會超出27mm。

六、證券市場

證券市場有時交易活躍，有時交易冷清。下面是你對市場的預測。

如果交易冷清，你會以平均價11元，賣出5萬股。

如果交易活躍，你會以平均價8元，賣出10萬股。

如果交易溫和，你會以平均價10元，賣出7.5萬股。

已知你的成本在每股5.5元到7.5元之間，平均是6.5元。請問接下來的交易，你的凈利潤會是多少？

取1000個隨機樣本，每個樣本有兩個數值：一個是證券的成本(5.5元到7.5元之間的均勻分布)，另一個是當前市場狀態(冷清、活躍、溫和，各有三分之一可能)。

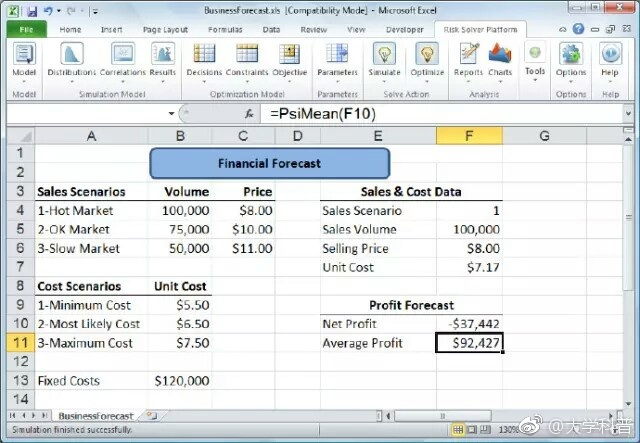
模擬計算得到，平均凈利潤為92, 427美元。

資料來源:妙思數學、百度百科

有方教育——我們的導師來自耶魯大學、麻省理工學院、斯坦福大學等世界頂尖名校，致力為讓中學生提供來自學界業界前沿的學術科研教育內容，旨在讓學生在親身實踐的過程中深入淺出地理解前沿科技。

項目主題——我們聚集頂尖學府導師資源，補足中美教育差距，力求為中國學生搭建連接世界科技的平臺。我們引領學生在世界前沿課題研究中參與科研教育，全面提升學生的自主思考、觀察分析、邏輯思維能力。我們為學生提供參加海外科研項目，幫助學生斬獲國際知名學術驚呆大獎、發表英語敘述論文，讓學生在提升申請競爭力的同事，獲得領跑優勢

責任編輯：