數據挖掘資料

https://blog.csdn.net/baimafujinji/article/details/53269040

在2006年12月召開的 IEEE 數據挖掘國際會議上（ICDM， International Conference on Data Mining），與會的各位專家選出了當時的十大數據挖掘算法（ top 10 data mining algorithms ），可以參見文獻【1】。本博客已經介紹過的位列十大算法之中的算法包括：

• [1]?k-means算法（http://blog.csdn.net/baimafujinji/article/details/50570824）
• [2] 支持向量機SVM（http://blog.csdn.net/baimafujinji/article/details/49885481）
• [3] EM算法（http://blog.csdn.net/baimafujinji/article/details/50626088）
• [4] 樸素貝葉斯算法（http://blog.csdn.net/baimafujinji/article/details/50441927）
• [5]?kkNN算法（http://blog.csdn.net/baimafujinji/article/details/6496222）
• [6] C4.5決策樹算法（http://blog.csdn.net/baimafujinji/article/details/53239581）

決策樹模型是一類算法的集合，在數據挖掘十大算法中，具體的決策樹算法占有兩席位置，即C4.5和CART算法。本文主要介紹分類回歸樹（CART，Classification And Regression Tree）也屬于一種決策樹，希望你在閱讀本文之前已經了解前文已經介紹過之內容：

• 《數據挖掘十大算法之決策樹詳解（1）》
• 《數據挖掘十大算法之決策樹詳解（2）》

歡迎關注白馬負金羈的博客?http://blog.csdn.net/baimafujinji，為保證公式、圖表得以正確顯示，強烈建議你從該地址上查看原版博文。本博客主要關注方向包括：數字圖像處理、算法設計與分析、數據結構、機器學習、數據挖掘、統計分析方法、自然語言處理。

---

CART生成

CART假設決策樹是二叉樹，內部結點特征的取值為“是”和“否”，左分支是取值為“是”的分支，右分支是取值為“否”的分支。這樣的決策樹等價于遞歸地二分每個特征，將輸入空間即特征空間劃分為有限個單元，并在這些單元上確定預測的概率分布，也就是在輸入給定的條件下輸出的條件概率分布。

CART算法由以下兩步組成：

1. 決策樹生成：基于訓練數據集生成決策樹，生成的決策樹要盡量大；
2. 決策樹剪枝：用驗證數據集對已生成的樹進行剪枝并選擇最優子樹，這時損失函數最小作為剪枝的標準。

CART決策樹的生成就是遞歸地構建二叉決策樹的過程。CART決策樹既可以用于分類也可以用于回歸。本文我們僅討論用于分類的CART。對分類樹而言，CART用Gini系數最小化準則來進行特征選擇，生成二叉樹。 CART生成算法如下：

輸入：訓練數據集DD，停止計算的條件：?
輸出：CART決策樹。

根據訓練數據集，從根結點開始，遞歸地對每個結點進行以下操作，構建二叉決策樹：

1. 設結點的訓練數據集為DD，計算現有特征對該數據集的Gini系數。此時，對每一個特征AA，對其可能取的每個值aa，根據樣本點對A=aA=a的測試為“是”或 “否”將DD分割成D1D1和D2D2兩部分，計算A=aA=a時的Gini系數。
2. 在所有可能的特征AA以及它們所有可能的切分點aa中，選擇Gini系數最小的特征及其對應的切分點作為最優特征與最優切分點。依最優特征與最優切分點，從現結點生成兩個子結點，將訓練數據集依特征分配到兩個子結點中去。
3. 對兩個子結點遞歸地調用步驟l~2，直至滿足停止條件。
4. 生成CART決策樹。

算法停止計算的條件是結點中的樣本個數小于預定閾值，或樣本集的Gini系數小于預定閾值（樣本基本屬于同一類），或者沒有更多特征。

---

一個具體的例子

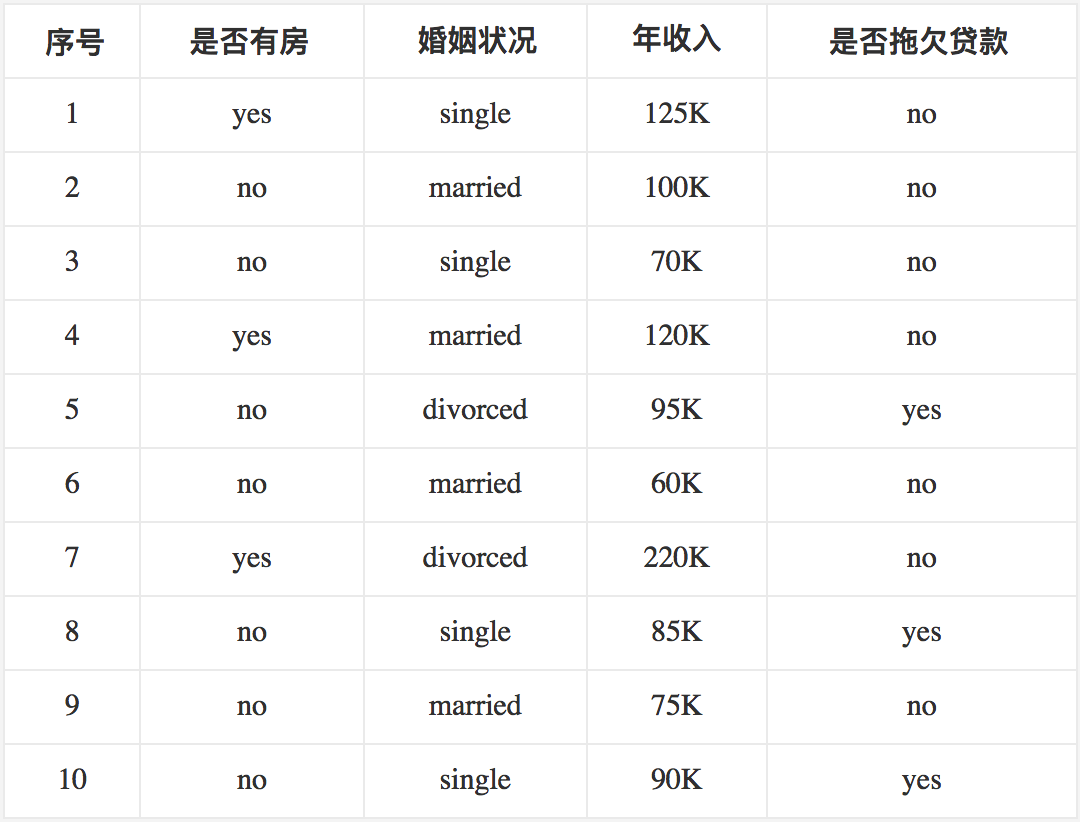
下面來看一個具體的例子。我們使用《數據挖掘十大算法之決策樹詳解（1）》中圖4-6所示的數據集來作為示例，為了便于后面的敘述，我們將其再列出如下：?

?

?

首先對數據集非類標號屬性{是否有房，婚姻狀況，年收入}分別計算它們的Gini系數增益，取Gini系數增益值最大的屬性作為決策樹的根節點屬性。根節點的Gini系數?

Gini(是否拖欠貸款)=1?(310)2?(710)2=0.42Gini(是否拖欠貸款)=1?(310)2?(710)2=0.42

當根據是否有房來進行劃分時，Gini系數增益計算過程為?

?

?

?

Gini(左子節點)=1?(03)2?(33)2=0Gini(右子節點)=1?(37)2?(47)2=0.4898Gini(左子節點)=1?(03)2?(33)2=0Gini(右子節點)=1?(37)2?(47)2=0.4898

?

Δ{是否有房}=0.42?710×0.4898?310×0=0.077Δ{是否有房}=0.42?710×0.4898?310×0=0.077

?

若按婚姻狀況屬性來劃分，屬性婚姻狀況有三個可能的取值{married，single，divorced}，分別計算劃分后的

• {married} | {single,divorced}
• {single} | {married,divorced}
• {divorced} | {single,married}

的Gini系數增益。?
當分組為{married} | {single,divorced}時，SlSl表示婚姻狀況取值為married的分組，SrSr表示婚姻狀況取值為single或者divorced的分組?

Δ{婚姻狀況}=0.42?410×0?610×[1?(36)2?(36)2]=0.12Δ{婚姻狀況}=0.42?410×0?610×[1?(36)2?(36)2]=0.12

當分組為{single} | {married,divorced}時，?

Δ{婚姻狀況}=0.42?410×0.5?610×[1?(16)2?(56)2]=0.053Δ{婚姻狀況}=0.42?410×0.5?610×[1?(16)2?(56)2]=0.053

當分組為{divorced} | {single,married}時，?

Δ{婚姻狀況}=0.42?210×0.5?810×[1?(28)2?(68)2]=0.02Δ{婚姻狀況}=0.42?210×0.5?810×[1?(28)2?(68)2]=0.02

對比計算結果，根據婚姻狀況屬性來劃分根節點時取Gini系數增益最大的分組作為劃分結果，也就是{married} | {single,divorced}。

?

最后考慮年收入屬性，我們發現它是一個連續的數值類型。我們在前面的文章里已經專門介紹過如何應對這種類型的數據劃分了。對此還不是很清楚的朋友可以參考之前的文章，這里不再贅述。

對于年收入屬性為數值型屬性，首先需要對數據按升序排序，然后從小到大依次用相鄰值的中間值作為分隔將樣本劃分為兩組。例如當面對年收入為60和70這兩個值時，我們算得其中間值為65。倘若以中間值65作為分割點。SlSl作為年收入小于65的樣本，SrSr表示年收入大于等于65的樣本，于是則得Gini系數增益為?

Δ(年收入)=0.42?110×0?910×[1?(69)2?(39)2]=0.02Δ(年收入)=0.42?110×0?910×[1?(69)2?(39)2]=0.02

其他值的計算同理可得，我們不再逐一給出計算過程，僅列出結果如下（最終我們取其中使得增益最大化的那個二分準則來作為構建二叉樹的準則）：?

?

注意，這與我們之前在《數據挖掘十大算法之決策樹詳解（1）》中得到的結果是一致的。最大化增益等價于最小化子女結點的不純性度量（Gini系數）的加權平均值，之前的表里我們列出的是Gini系數的加權平均值，現在的表里給出的是Gini系數增益。現在我們希望最大化Gini系數的增益。根據計算知道，三個屬性劃分根節點的增益最大的有兩個：年收入屬性和婚姻狀況，他們的增益都為0.12。此時，選取首先出現的屬性作為第一次劃分。

?

接下來，采用同樣的方法，分別計算剩下屬性，其中根節點的Gini系數為（此時是否拖欠貸款的各有3個records）

Gini(是否拖欠貸款)=1?(36)2?(36)2=0.5Gini(是否拖欠貸款)=1?(36)2?(36)2=0.5

與前面的計算過程類似，對于是否有房屬性，可得?

Δ{是否有房}=0.5?46×[1?(34)2?(14)2]?26×0=0.25Δ{是否有房}=0.5?46×[1?(34)2?(14)2]?26×0=0.25

對于年收入屬性則有：

?

?

?

?

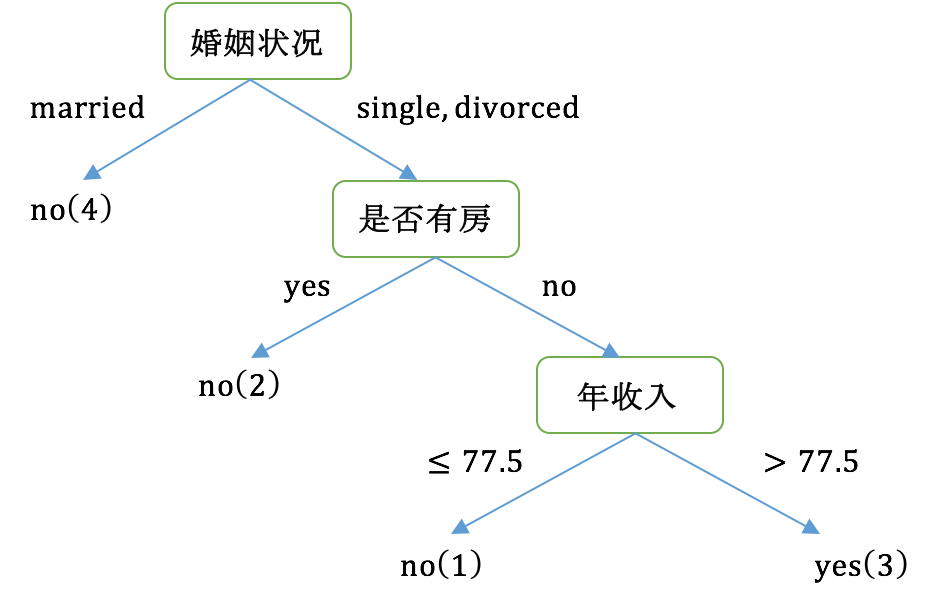
最后我們構建的CART如下圖所示：

?

?

?

最后我們總結一下，CART和C4.5的主要區別：

• C4.5采用信息增益率來作為分支特征的選擇標準，而CART則采用Gini系數；
• C4.5不一定是二叉樹，但CART一定是二叉樹。

---

關于過擬合以及剪枝

決策樹很容易發生過擬合，也就是由于對train數據集適應得太好，反而在test數據集上表現得不好。這個時候我們要么是通過閾值控制終止條件避免樹形結構分支過細，要么就是通過對已經形成的決策樹進行剪枝來避免過擬合。另外一個克服過擬合的手段就是基于Bootstrap的思想建立隨機森林（Random Forest）。關于剪枝的內容可以參考文獻【2】以了解更多，如果有機會我也可能在后續的文章里討論它。

?