（一）紅黑樹

紅黑樹是一種自平衡二叉查找樹，也被稱為"對稱二叉B樹"，它可以在O(logn)時間內利用 O(logn)的空間來完成查找、插入、刪除操作。紅黑樹的讀操作與普通二叉查找樹相同，而插入和刪除操作可能會破壞紅黑樹的規則，需要進行恢復操作。恢復紅黑樹的性質需要少量的顏色變更（實際是非常快速的）和不超過三次樹旋轉（對于插入操作是兩次），雖然插入和刪除很復雜，但操作時間仍可以保持為O(logn)。

紅黑樹的規則：

1.節點是紅色或和黑色
2.根節點是黑色
3.所有的葉子節點都是黑色（葉子節點是NIL節點，實際應用時可以有數據）
4.每個紅色節點必須有兩個黑色的子節點，從葉子節點到根節點不能有兩個連續的紅色節點。
5.從任意節點到每個葉子節點的簡單路徑都包含相同數量的黑色節點。

（二）B+樹

（1）B+樹常用于數據庫和文件系統中，B+樹能夠保持數據穩定有序，其插入與修改擁有較穩定的對數時間復雜度。B+ 樹自底向上插入，這與二叉樹恰好相反。
（2）B+樹與B樹的主要區別：1.B+樹中只有葉子節點會帶有指向記錄的指針，而B樹所有節點都有指針，在內部節點出現的索引項不會再出現在葉子節點中。（B+樹的所有全量數據都在葉子節點，而B樹每個節點都是全量數據）2.B+樹中所有葉子節點都是通過指針連接在一起，而B樹不會。

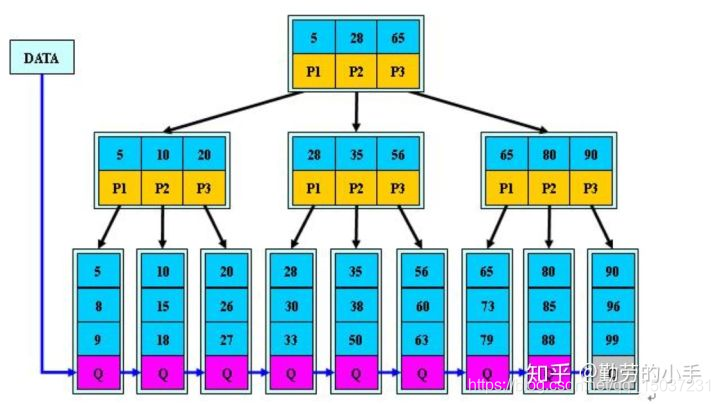
（二）兩種樹的區別

紅黑樹結構的數據常常存在于主存中，主要用于快速查找。樹的每個節點存儲的數據量比較小，cpu通過與主存少量的交互就能獲取樹的全部數據，并快速的查找到所需數據。而B+樹形式的數據常常存在于SSD或磁盤中，由于樹的深度比較小(一般3~4)，能夠減少cpu于磁盤間的交互時間。