文章目錄
- 線性數據結構
- 1. 數組
- 2. 鏈表
- 2.1. 鏈表簡介
- 2.2. 鏈表分類
- 2.2.1. 單鏈表
- 2.2.2. 循環鏈表
- 2.2.3. 雙向鏈表
- 2.2.4. 雙向循環鏈表
- 2.3. 應用場景
- 2.4. 數組 vs 鏈表
- 3. 棧
- 3.1. 棧簡介
- 3.2. 棧的常見應用常見應用場景
- 3.2.1. 實現瀏覽器的回退和前進功能
- 3.2.2. 檢查符號是否成對出現
- 3.2.3. 反轉字符串
- 3.2.4. 維護函數調用
- 3.3. 棧的實現
- 4. 隊列
- 4.1. 隊列簡介
- 4.2. 隊列分類
- 4.2.1. 單隊列
- 4.2.2. 循環隊列
- 4.3. 常見應用場景
- 樹
- 二叉樹的分類
- 滿二叉樹
- 完全二叉樹
- 平衡二叉樹
- 紅黑樹
- 二叉樹的存儲
- 鏈式存儲
- 順序存儲
- 二叉樹的遍歷
- 先序遍歷
- 中序遍歷
- 后序遍歷
- 圖
- 圖的基本概念
- 頂點
- 邊
- 度
- 無向圖和有向圖
- 無權圖和帶權圖
- 圖的存儲
- 鄰接矩陣存儲
- 鄰接表存儲
- 圖的搜索
- 廣度優先搜索
- 深度優先搜索
- 堆
- 什么是堆
- 堆的用途
- 堆的分類
- 堆的存儲
- 堆的操作
- 插入元素
- 刪除堆頂元素
- 自底向上堆化
- 自頂向下堆化
- 堆的操作總結
- 堆排序
- 建堆
- 排序
- 排序
線性數據結構
1. 數組
數組(Array) 是一種很常見的數據結構。它由相同類型的元素(element)組成,并且是使用一塊連續的內存來存儲。
我們直接可以利用元素的索引(index)可以計算出該元素對應的存儲地址。
數組的特點是:提供隨機訪問 并且容量有限。
假如數組的長度為 n。
訪問:O(1)//訪問特定位置的元素
插入:O(n )//最壞的情況發生在插入發生在數組的首部并需要移動所有元素時
刪除:O(n)//最壞的情況發生在刪除數組的開頭發生并需要移動第一元素后面所有的元素時Copy to clipboardErrorCopied

2. 鏈表
2.1. 鏈表簡介
鏈表(LinkedList) 雖然是一種線性表,但是并不會按線性的順序存儲數據,使用的不是連續的內存空間來存儲數據。
鏈表的插入和刪除操作的復雜度為 O(1) ,只需要知道目標位置元素的上一個元素即可。但是,在查找一個節點或者訪問特定位置的節點的時候復雜度為 O(n) 。
使用鏈表結構可以克服數組需要預先知道數據大小的缺點,鏈表結構可以充分利用計算機內存空間,實現靈活的內存動態管理。但鏈表不會節省空間,相比于數組會占用更多的空間,因為鏈表中每個節點存放的還有指向其他節點的指針。除此之外,鏈表不具有數組隨機讀取的優點。
2.2. 鏈表分類
常見鏈表分類:
- 單鏈表
- 雙向鏈表
- 循環鏈表
- 雙向循環鏈表
假如鏈表中有n個元素。
訪問:O(n)//訪問特定位置的元素
插入刪除:O(1)//必須要要知道插入元素的位置Copy to clipboardErrorCopied
2.2.1. 單鏈表
單鏈表 單向鏈表只有一個方向,結點只有一個后繼指針 next 指向后面的節點。因此,鏈表這種數據結構通常在物理內存上是不連續的。我們習慣性地把第一個結點叫作頭結點,鏈表通常有一個不保存任何值的 head 節點(頭結點),通過頭結點我們可以遍歷整個鏈表。尾結點通常指向 null。
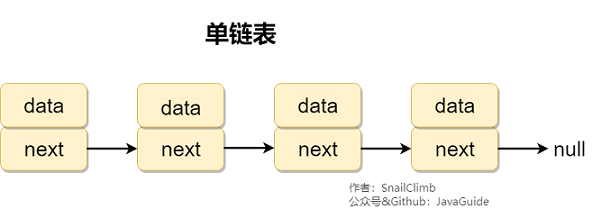
2.2.2. 循環鏈表
循環鏈表 其實是一種特殊的單鏈表,和單鏈表不同的是循環鏈表的尾結點不是指向 null,而是指向鏈表的頭結點。
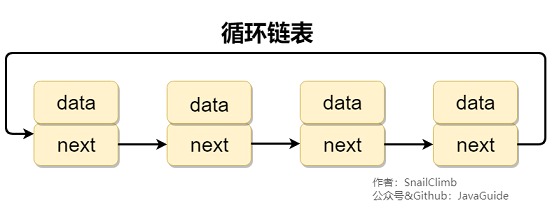
2.2.3. 雙向鏈表
雙向鏈表 包含兩個指針,一個 prev 指向前一個節點,一個 next 指向后一個節點。
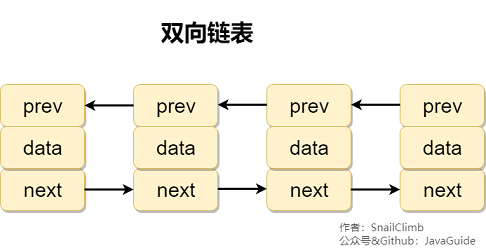
2.2.4. 雙向循環鏈表
雙向循環鏈表 最后一個節點的 next 指向 head,而 head 的 prev 指向最后一個節點,構成一個環。
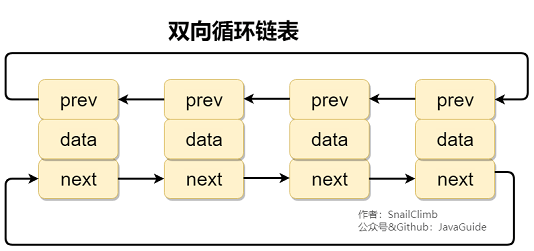
2.3. 應用場景
- 如果需要支持隨機訪問的話,鏈表沒辦法做到。
- 如果需要存儲的數據元素的個數不確定,并且需要經常添加和刪除數據的話,使用鏈表比較合適。
- 如果需要存儲的數據元素的個數確定,并且不需要經常添加和刪除數據的話,使用數組比較合適。
2.4. 數組 vs 鏈表
- 數組支持隨機訪問,而鏈表不支持。
- 數組使用的是連續內存空間對 CPU 的緩存機制友好,鏈表則相反。
- 數組的大小固定,而鏈表則天然支持動態擴容。如果聲明的數組過小,需要另外申請一個更大的內存空間存放數組元素,然后將原數組拷貝進去,這個操作是比較耗時的!
3. 棧
3.1. 棧簡介
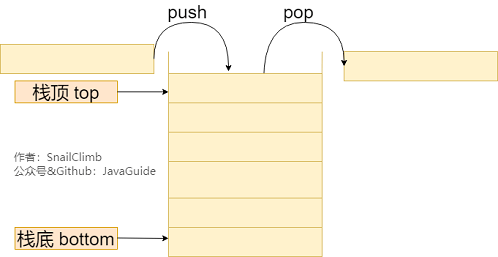
棧 (stack)只允許在有序的線性數據集合的一端(稱為棧頂 top)進行加入數據(push)和移除數據(pop)。因而按照 后進先出(LIFO, Last In First Out) 的原理運作。在棧中,push 和 pop 的操作都發生在棧頂。
棧常用一維數組或鏈表來實現,用數組實現的棧叫作 順序棧 ,用鏈表實現的棧叫作 鏈式棧 。
假設堆棧中有n個元素。
訪問:O(n)//最壞情況
插入刪除:O(1)//頂端插入和刪除元素Copy to clipboardErrorCopied
3.2. 棧的常見應用常見應用場景
當我們我們要處理的數據只涉及在一端插入和刪除數據,并且滿足 后進先出(LIFO, Last In First Out) 的特性時,我們就可以使用棧這個數據結構。
3.2.1. 實現瀏覽器的回退和前進功能
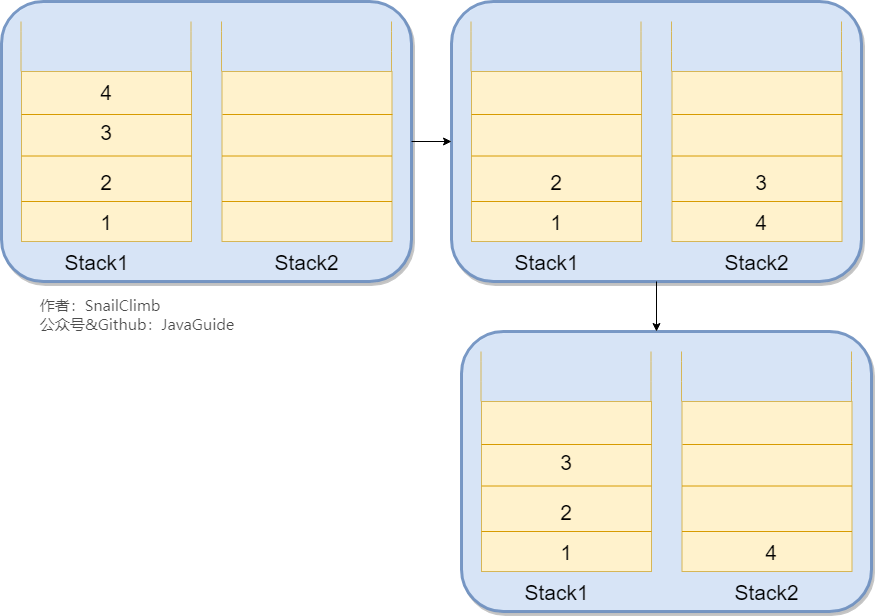
我們只需要使用兩個棧(Stack1 和 Stack2)和就能實現這個功能。比如你按順序查看了 1,2,3,4 這四個頁面,我們依次把 1,2,3,4 這四個頁面壓入 Stack1 中。當你想回頭看 2 這個頁面的時候,你點擊回退按鈕,我們依次把 4,3 這兩個頁面從 Stack1 彈出,然后壓入 Stack2 中。假如你又想回到頁面 3,你點擊前進按鈕,我們將 3 頁面從 Stack2 彈出,然后壓入到 Stack1 中。示例圖如下:
3.2.2. 檢查符號是否成對出現
給定一個只包括
'(',')','{','}','[',']'的字符串,判斷該字符串是否有效。有效字符串需滿足:
- 左括號必須用相同類型的右括號閉合。
- 左括號必須以正確的順序閉合。
比如 “()”、"()[]{}"、"{[]}" 都是有效字符串,而 “(]” 、"([)]" 則不是。
這個問題實際是 Leetcode 的一道題目,我們可以利用棧 Stack 來解決這個問題。
- 首先我們將括號間的對應規則存放在
Map中,這一點應該毋容置疑; - 創建一個棧。遍歷字符串,如果字符是左括號就直接加入
stack中,否則將stack的棧頂元素與這個括號做比較,如果不相等就直接返回 false。遍歷結束,如果stack為空,返回true。
public boolean isValid(String s){// 括號之間的對應規則HashMap<Character, Character> mappings = new HashMap<Character, Character>();mappings.put(')', '(');mappings.put('}', '{');mappings.put(']', '[');Stack<Character> stack = new Stack<Character>();char[] chars = s.toCharArray();for (int i = 0; i < chars.length; i++) {if (mappings.containsKey(chars[i])) {char topElement = stack.empty() ? '#' : stack.pop();if (topElement != mappings.get(chars[i])) {return false;}} else {stack.push(chars[i]);}}return stack.isEmpty();
}Copy to clipboardErrorCopied
3.2.3. 反轉字符串
將字符串中的每個字符先入棧再出棧就可以了。
3.2.4. 維護函數調用
最后一個被調用的函數必須先完成執行,符合棧的 后進先出(LIFO, Last In First Out) 特性。
3.3. 棧的實現
棧既可以通過數組實現,也可以通過鏈表來實現。不管基于數組還是鏈表,入棧、出棧的時間復雜度都為 O(1)。
下面我們使用數組來實現一個棧,并且這個棧具有push()、pop()(返回棧頂元素并出棧)、peek() (返回棧頂元素不出棧)、isEmpty()、size()這些基本的方法。
提示:每次入棧之前先判斷棧的容量是否夠用,如果不夠用就用
Arrays.copyOf()進行擴容;
public class MyStack {private int[] storage;//存放棧中元素的數組private int capacity;//棧的容量private int count;//棧中元素數量private static final int GROW_FACTOR = 2;//不帶初始容量的構造方法。默認容量為8public MyStack() {this.capacity = 8;this.storage=new int[8];this.count = 0;}//帶初始容量的構造方法public MyStack(int initialCapacity) {if (initialCapacity < 1)throw new IllegalArgumentException("Capacity too small.");this.capacity = initialCapacity;this.storage = new int[initialCapacity];this.count = 0;}//入棧public void push(int value) {if (count == capacity) {ensureCapacity();}storage[count++] = value;}//確保容量大小private void ensureCapacity() {int newCapacity = capacity * GROW_FACTOR;storage = Arrays.copyOf(storage, newCapacity);capacity = newCapacity;}//返回棧頂元素并出棧private int pop() {if (count == 0)throw new IllegalArgumentException("Stack is empty.");count--;return storage[count];}//返回棧頂元素不出棧private int peek() {if (count == 0){throw new IllegalArgumentException("Stack is empty.");}else {return storage[count-1];}}//判斷棧是否為空private boolean isEmpty() {return count == 0;}//返回棧中元素的個數private int size() {return count;}}Copy to clipboardErrorCopied
驗證
MyStack myStack = new MyStack(3);
myStack.push(1);
myStack.push(2);
myStack.push(3);
myStack.push(4);
myStack.push(5);
myStack.push(6);
myStack.push(7);
myStack.push(8);
System.out.println(myStack.peek());//8
System.out.println(myStack.size());//8
for (int i = 0; i < 8; i++) {System.out.println(myStack.pop());
}
System.out.println(myStack.isEmpty());//true
myStack.pop();//報錯:java.lang.IllegalArgumentException: Stack is empty.Copy to clipboardErrorCopied
4. 隊列
4.1. 隊列簡介
隊列 是 先進先出( FIFO,First In, First Out) 的線性表。在具體應用中通常用鏈表或者數組來實現,用數組實現的隊列叫作 順序隊列 ,用鏈表實現的隊列叫作 鏈式隊列 。隊列只允許在后端(rear)進行插入操作也就是 入隊 enqueue,在前端(front)進行刪除操作也就是出隊 dequeue
隊列的操作方式和堆棧類似,唯一的區別在于隊列只允許新數據在后端進行添加。
假設隊列中有n個元素。
訪問:O(n)//最壞情況
插入刪除:O(1)//后端插入前端刪除元素Copy to clipboardErrorCopied

4.2. 隊列分類
4.2.1. 單隊列
單隊列就是常見的隊列, 每次添加元素時,都是添加到隊尾。單隊列又分為 順序隊列(數組實現) 和 鏈式隊列(鏈表實現)。
順序隊列存在“假溢出”的問題也就是明明有位置卻不能添加的情況。
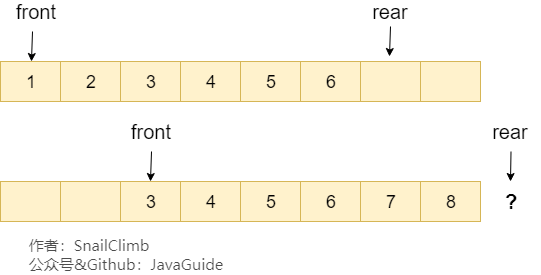
假設下圖是一個順序隊列,我們將前兩個元素 1,2 出隊,并入隊兩個元素 7,8。當進行入隊、出隊操作的時候,front 和 rear 都會持續往后移動,當 rear 移動到最后的時候,我們無法再往隊列中添加數據,即使數組中還有空余空間,這種現象就是 ”假溢出“ 。除了假溢出問題之外,如下圖所示,當添加元素 8 的時候,rear 指針移動到數組之外(越界)。
為了避免當只有一個元素的時候,隊頭和隊尾重合使處理變得麻煩,所以引入兩個指針,front 指針指向對頭元素,rear 指針指向隊列最后一個元素的下一個位置,這樣當 front 等于 rear 時,此隊列不是還剩一個元素,而是空隊列。——From 《大話數據結構》
4.2.2. 循環隊列
循環隊列可以解決順序隊列的假溢出和越界問題。解決辦法就是:從頭開始,這樣也就會形成頭尾相接的循環,這也就是循環隊列名字的由來。
還是用上面的圖,我們將 rear 指針指向數組下標為 0 的位置就不會有越界問題了。當我們再向隊列中添加元素的時候, rear 向后移動。
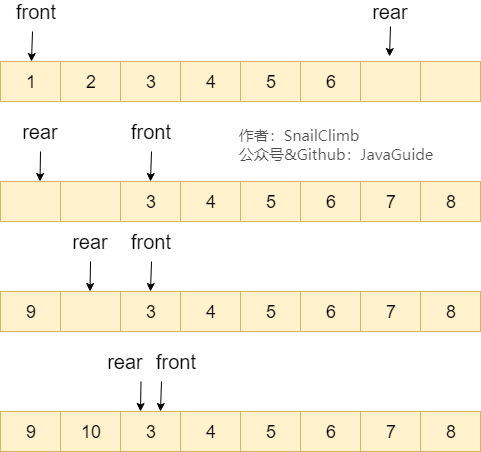
順序隊列中,我們說 front==rear 的時候隊列為空,循環隊列中則不一樣,也可能為滿,如上圖所示。解決辦法有兩種:
- 可以設置一個標志變量
flag,當front==rear并且flag=0的時候隊列為空,當front==rear并且flag=1的時候隊列為滿。 - 隊列為空的時候就是
front==rear,隊列滿的時候,我們保證數組還有一個空閑的位置,rear 就指向這個空閑位置,如下圖所示,那么現在判斷隊列是否為滿的條件就是:(rear+1) % QueueSize= front。

4.3. 常見應用場景
當我們需要按照一定順序來處理數據的時候可以考慮使用隊列這個數據結構。
- 阻塞隊列: 阻塞隊列可以看成在隊列基礎上加了阻塞操作的隊列。當隊列為空的時候,出隊操作阻塞,當隊列滿的時候,入隊操作阻塞。使用阻塞隊列我們可以很容易實現“生產者 - 消費者“模型。
- 線程池中的請求/任務隊列: 線程池中沒有空閑線程時,新的任務請求線程資源時,線程池該如何處理呢?答案是將這些請求放在隊列中,當有空閑線程的時候,會循環中反復從隊列中獲取任務來執行。隊列分為無界隊列(基于鏈表)和有界隊列(基于數組)。無界隊列的特點就是可以一直入列,除非系統資源耗盡,比如 :
FixedThreadPool使用無界隊列LinkedBlockingQueue。但是有界隊列就不一樣了,當隊列滿的話后面再有任務/請求就會拒絕,在 Java 中的體現就是會拋出java.util.concurrent.RejectedExecutionException異常。 - Linux 內核進程隊列(按優先級排隊)
- 現實生活中的派對,播放器上的播放列表;
- 消息隊列
- 等等…
樹
樹就是一種類似現實生活中的樹的數據結構(倒置的樹)。任何一顆非空樹只有一個根節點。
一棵樹具有以下特點:
- 一棵樹中的任意兩個結點有且僅有唯一的一條路徑連通。
- 一棵樹如果有 n 個結點,那么它一定恰好有 n-1 條邊。
- 一棵樹不包含回路。
下圖就是一顆樹,并且是一顆二叉樹。
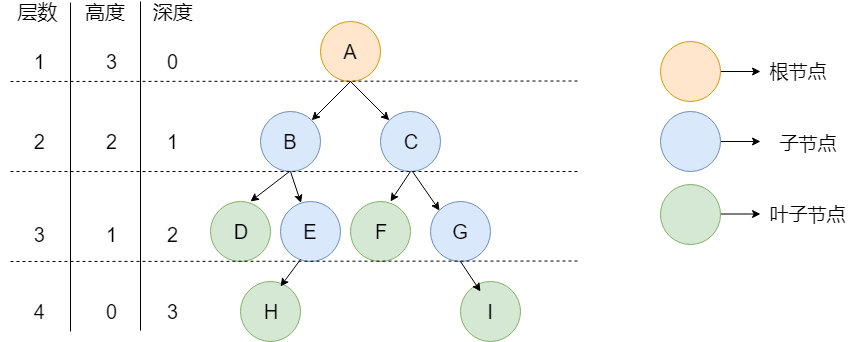
如上圖所示,通過上面這張圖說明一下樹中的常用概念:
- 節點 :樹中的每個元素都可以統稱為節點。
- 根節點 :頂層節點或者說沒有父節點的節點。上圖中 A 節點就是根節點。
- 父節點 :若一個節點含有子節點,則這個節點稱為其子節點的父節點。上圖中的 B 節點是 D 節點、E 節點的父節點。
- 子節點 :一個節點含有的子樹的根節點稱為該節點的子節點。上圖中 D 節點、E 節點是 B 節點的子節點。
- 兄弟節點 :具有相同父節點的節點互稱為兄弟節點。上圖中 D 節點、E 節點的共同父節點是 B 節點,故 D 和 E 為兄弟節點。
- 葉子節點 :沒有子節點的節點。上圖中的 D、F、H、I 都是葉子節點。
- 節點的高度 :該節點到葉子節點的最長路徑所包含的邊數。
- 節點的深度 :根節點到該節點的路徑所包含的邊數
- 節點的層數 :節點的深度+1。
- 樹的高度 :根節點的高度。
二叉樹的分類
二叉樹(Binary tree)是每個節點最多只有兩個分支(即不存在分支度大于 2 的節點)的樹結構。
二叉樹 的分支通常被稱作“左子樹”或“右子樹”。并且,二叉樹 的分支具有左右次序,不能隨意顛倒。
二叉樹 的第 i 層至多擁有 2^(i-1) 個節點,深度為 k 的二叉樹至多總共有 2^k-1 個節點
滿二叉樹
一個二叉樹,如果每一個層的結點數都達到最大值,則這個二叉樹就是 滿二叉樹。也就是說,如果一個二叉樹的層數為 K,且結點總數是(2^k) -1 ,則它就是 滿二叉樹。如下圖所示:
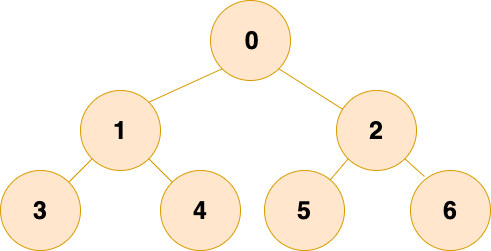
完全二叉樹
除最后一層外,若其余層都是滿的,并且最后一層或者是滿的,或者是在右邊缺少連續若干節點,則這個二叉樹就是 完全二叉樹 。
大家可以想象為一棵樹從根結點開始擴展,擴展完左子節點才能開始擴展右子節點,每擴展完一層,才能繼續擴展下一層。如下圖所示:
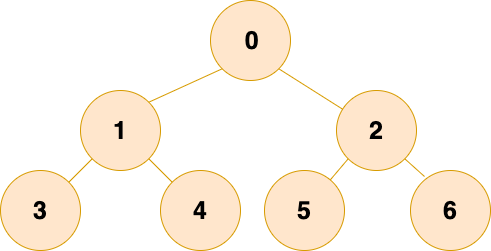
完全二叉樹有一個很好的性質:父結點和子節點的序號有著對應關系。
細心的小伙伴可能發現了,當根節點的值為 1 的情況下,若父結點的序號是 i,那么左子節點的序號就是 2i,右子節點的序號是 2i+1。這個性質使得完全二叉樹利用數組存儲時可以極大地節省空間,以及利用序號找到某個節點的父結點和子節點,后續二叉樹的存儲會詳細介紹。
平衡二叉樹
平衡二叉樹 是一棵二叉排序樹,且具有以下性質:
- 可以是一棵空樹
- 如果不是空樹,它的左右兩個子樹的高度差的絕對值不超過 1,并且左右兩個子樹都是一棵平衡二叉樹。
平衡二叉樹的常用實現方法有 紅黑樹、AVL 樹、替罪羊樹、加權平衡樹、伸展樹 等。
在給大家展示平衡二叉樹之前,先給大家看一棵樹:
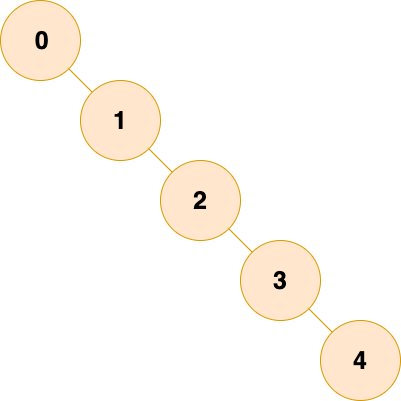
你管這玩意兒叫樹???
沒錯,這玩意兒還真叫樹,只不過這棵樹已經退化為一個鏈表了,我們管它叫 斜樹。
如果這樣,那我為啥不直接用鏈表呢?
誰說不是呢?
二叉樹相比于鏈表,由于父子節點以及兄弟節點之間往往具有某種特殊的關系,這種關系使得我們在樹中對數據進行搜索和修改時,相對于鏈表更加快捷便利。
但是,如果二叉樹退化為一個鏈表了,那么那么樹所具有的優秀性質就難以表現出來,效率也會大打折,為了避免這樣的情況,我們希望每個做 “家長”(父結點) 的,都 一碗水端平,分給左兒子和分給右兒子的盡可能一樣多,相差最多不超過一層,如下圖所示:
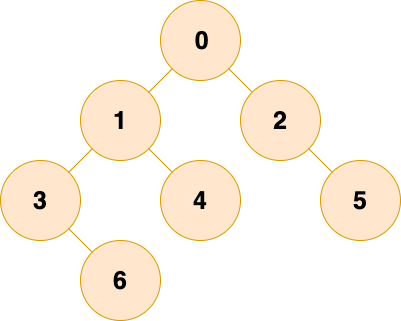
紅黑樹
紅黑樹特點 :
- 每個節點非紅即黑;
- 根節點總是黑色的;
- 每個葉子節點都是黑色的空節點(NIL節點);
- 如果節點是紅色的,則它的子節點必須是黑色的(反之不一定);
- 從根節點到葉節點或空子節點的每條路徑,必須包含相同數目的黑色節點(即相同的黑色高度)。
紅黑樹的應用 :TreeMap、TreeSet以及JDK1.8的HashMap底層都用到了紅黑樹。
為什么要用紅黑樹? 簡單來說紅黑樹就是為了解決二叉查找樹的缺陷,因為二叉查找樹在某些情況下會退化成一個線性結構。詳細了解可以查看 漫畫:什么是紅黑樹?(也介紹到了二叉查找樹,非常推薦)
相關閱讀 :《紅黑樹深入剖析及Java實現》(美團點評技術團隊)
二叉樹的存儲
二叉樹的存儲主要分為 鏈式存儲 和 順序存儲 兩種:
鏈式存儲
和鏈表類似,二叉樹的鏈式存儲依靠指針將各個節點串聯起來,不需要連續的存儲空間。
每個節點包括三個屬性:
- 數據 data。data 不一定是單一的數據,根據不同情況,可以是多個具有不同類型的數據。
- 左節點指針 left
- 右節點指針 right。
可是 JAVA 沒有指針啊!
那就直接引用對象唄(別問我對象哪里找)
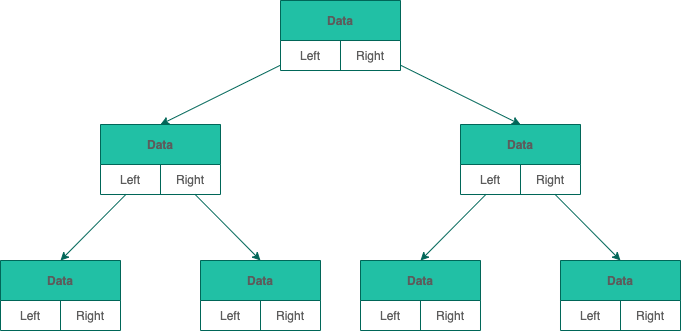
順序存儲
順序存儲就是利用數組進行存儲,數組中的每一個位置僅存儲節點的 data,不存儲左右子節點的指針,子節點的索引通過數組下標完成。根結點的序號為 1,對于每個節點 Node,假設它存儲在數組中下標為 i 的位置,那么它的左子節點就存儲在 2 _ i 的位置,它的右子節點存儲在下標為 2 _ i+1 的位置。
一棵完全二叉樹的數組順序存儲如下圖所示:
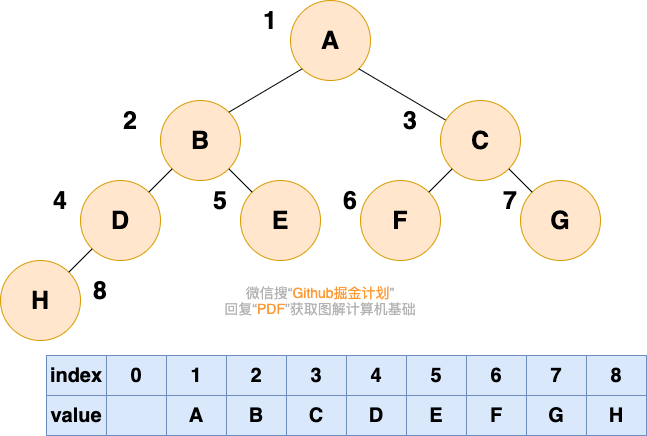
大家可以試著填寫一下存儲如下二叉樹的數組,比較一下和完全二叉樹的順序存儲有何區別:
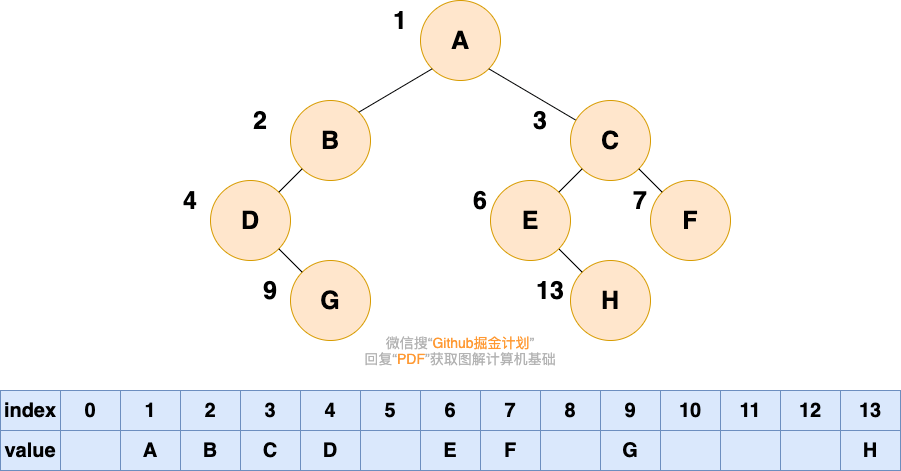
可以看到,如果我們要存儲的二叉樹不是完全二叉樹,在數組中就會出現空隙,導致內存利用率降低
二叉樹的遍歷
先序遍歷
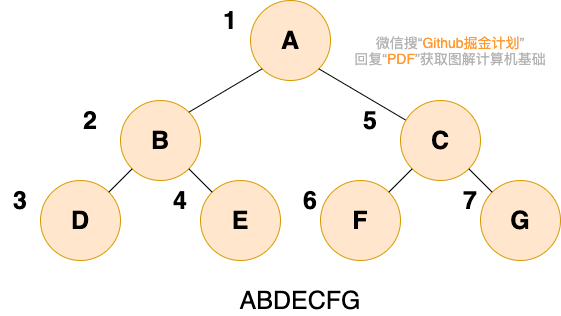
二叉樹的先序遍歷,就是先輸出根結點,再遍歷左子樹,最后遍歷右子樹,遍歷左子樹和右子樹的時候,同樣遵循先序遍歷的規則,也就是說,我們可以遞歸實現先序遍歷。
代碼如下:
public void preOrder(TreeNode root){if(root == null){return;}system.out.println(root.data);preOrder(root.left);preOrder(root.right);
}Copy to clipboardErrorCopied
中序遍歷
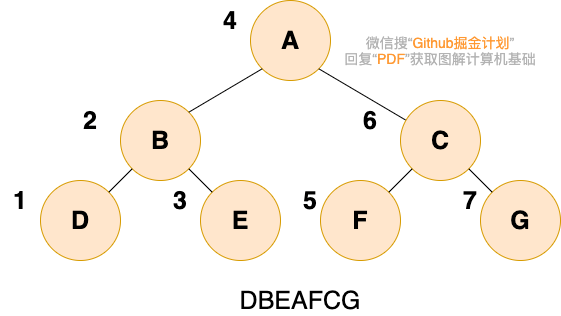
二叉樹的中序遍歷,就是先遞歸中序遍歷左子樹,再輸出根結點的值,再遞歸中序遍歷右子樹,大家可以想象成一巴掌把樹壓扁,父結點被拍到了左子節點和右子節點的中間,如下圖所示:

代碼如下:
public void inOrder(TreeNode root){if(root == null){return;}inOrder(root.left);system.out.println(root.data);inOrder(root.right);
}Copy to clipboardErrorCopied
后序遍歷
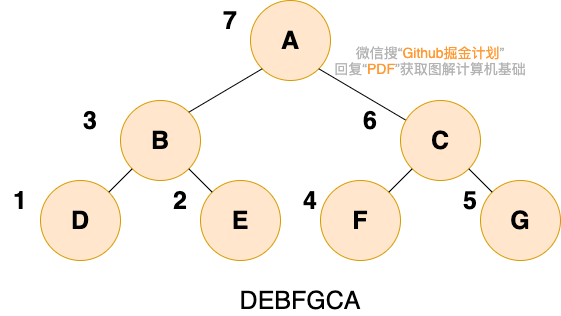
二叉樹的后序遍歷,就是先遞歸后序遍歷左子樹,再遞歸后序遍歷右子樹,最后輸出根結點的值
代碼如下:
public void postOrder(TreeNode root){if(root == null){return;}postOrder(root.left);postOrder(root.right);system.out.println(root.data);
}
圖
圖是一種較為復雜的非線性結構。 為啥說其較為復雜呢?
根據前面的內容,我們知道:
- 線性數據結構的元素滿足唯一的線性關系,每個元素(除第一個和最后一個外)只有一個直接前趨和一個直接后繼。
- 樹形數據結構的元素之間有著明顯的層次關系。
但是,圖形結構的元素之間的關系是任意的。
何為圖呢? 簡單來說,圖就是由頂點的有窮非空集合和頂點之間的邊組成的集合。通常表示為:G(V,E),其中,G表示一個圖,V表示頂點的集合,E表示邊的集合。
下圖所展示的就是圖這種數據結構,并且還是一張有向圖。
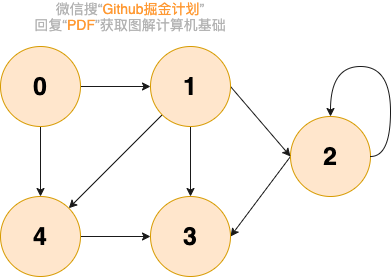
圖在我們日常生活中的例子很多!比如我們在社交軟件上好友關系就可以用圖來表示。
圖的基本概念
頂點
圖中的數據元素,我們稱之為頂點,圖至少有一個頂點(非空有窮集合)
對應到好友關系圖,每一個用戶就代表一個頂點。
邊
頂點之間的關系用邊表示。
對應到好友關系圖,兩個用戶是好友的話,那兩者之間就存在一條邊。
度
度表示一個頂點包含多少條邊,在有向圖中,還分為出度和入度,出度表示從該頂點出去的邊的條數,入度表示進入該頂點的邊的條數。
對應到好友關系圖,度就代表了某個人的好友數量。
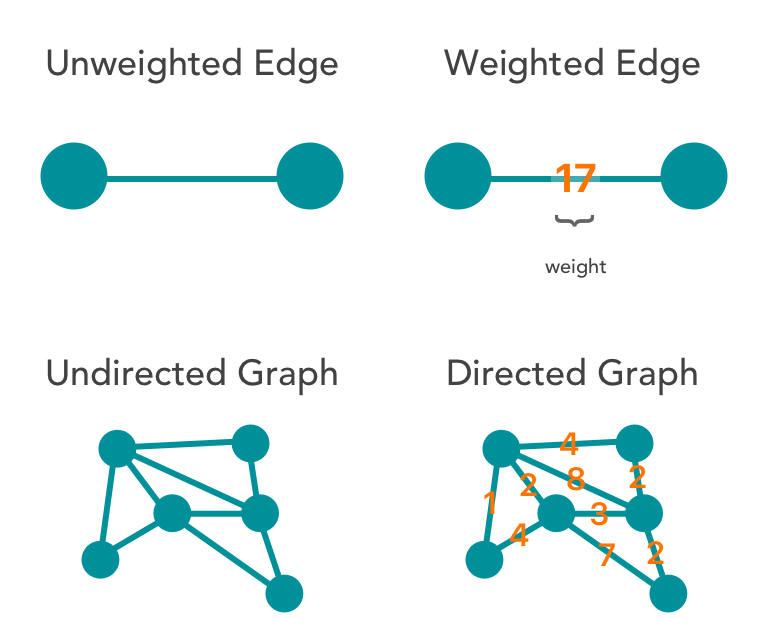
無向圖和有向圖
邊表示的是頂點之間的關系,有的關系是雙向的,比如同學關系,A是B的同學,那么B也肯定是A的同學,那么在表示A和B的關系時,就不用關注方向,用不帶箭頭的邊表示,這樣的圖就是無向圖。
有的關系是有方向的,比如父子關系,師生關系,微博的關注關系,A是B的爸爸,但B肯定不是A的爸爸,A關注B,B不一定關注A。在這種情況下,我們就用帶箭頭的邊表示二者的關系,這樣的圖就是有向圖。
無權圖和帶權圖
對于一個關系,如果我們只關心關系的有無,而不關心關系有多強,那么就可以用無權圖表示二者的關系。
對于一個關系,如果我們既關心關系的有無,也關心關系的強度,比如描述地圖上兩個城市的關系,需要用到距離,那么就用帶權圖來表示,帶權圖中的每一條邊一個數值表示權值,代表關系的強度。
圖的存儲
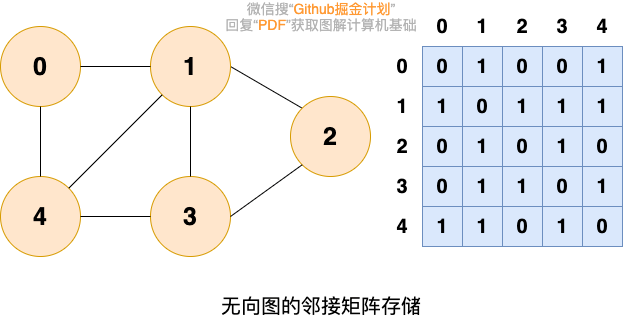
鄰接矩陣存儲
鄰接矩陣將圖用二維矩陣存儲,是一種較為直觀的表示方式。
如果第i個頂點和第j個頂點之間有關系,且關系權值為n,則 A[i][j]=n 。
在無向圖中,我們只關心關系的有無,所以當頂點i和頂點j有關系時,A[i][j]=1,當頂點i和頂點j沒有關系時,A[i][j]=0。如下圖所示:
值得注意的是:無向圖的鄰接矩陣是一個對稱矩陣,因為在無向圖中,頂點i和頂點j有關系,則頂點j和頂點i必有關系。
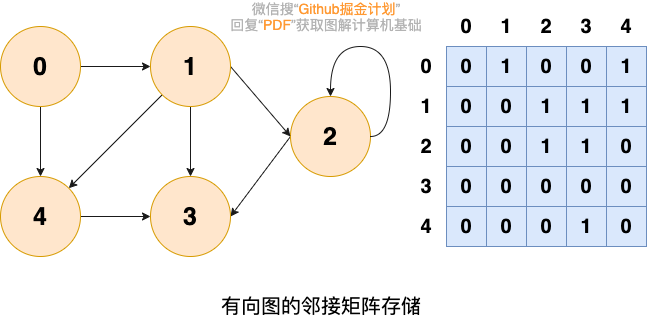
鄰接矩陣存儲的方式優點是簡單直接(直接使用一個二維數組即可),并且,在獲取兩個定點之間的關系的時候也非常高效(直接獲取指定位置的數組元素的值即可)。但是,這種存儲方式的缺點也比較明顯,那就是比較浪費空間,
鄰接表存儲
針對上面鄰接矩陣比較浪費內存空間的問題,誕生了圖的另外一種存儲方法—鄰接表 。
鄰接鏈表使用一個鏈表來存儲某個頂點的所有后繼相鄰頂點。對于圖中每個頂點Vi,把所有鄰接于Vi的頂點Vj鏈成一個單鏈表,這個單鏈表稱為頂點Vi的 鄰接表。如下圖所示:
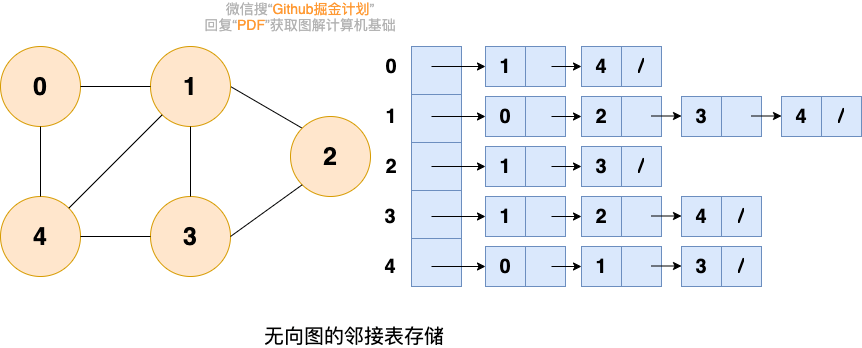
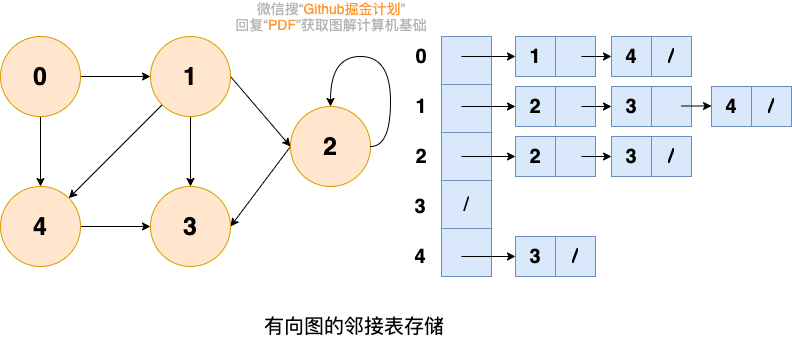
大家可以數一數鄰接表中所存儲的元素的個數以及圖中邊的條數,你會發現:
- 在無向圖中,鄰接表元素個數等于邊的條數的兩倍,如左圖所示的無向圖中,邊的條數為7,鄰接表存儲的元素個數為14。
- 在有向圖中,鄰接表元素個數等于邊的條數,如右圖所示的有向圖中,邊的條數為8,鄰接表存儲的元素個數為8。
圖的搜索
廣度優先搜索
廣度優先搜索就像水面上的波紋一樣一層一層向外擴展,如下圖所示:
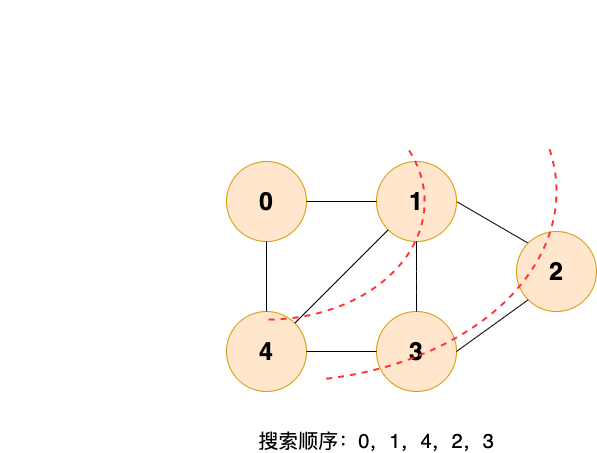
廣度優先搜索的具體實現方式用到了之前所學過的線性數據結構——隊列 。具體過程如下圖所示:
第1步:
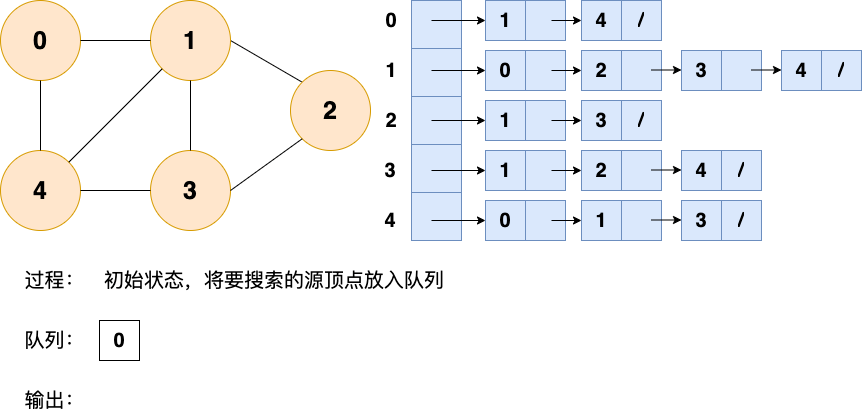
第2步:
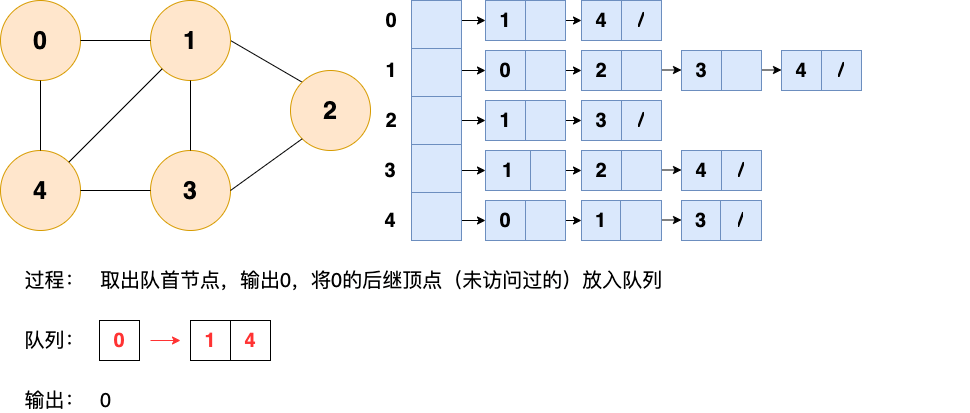
第3步:
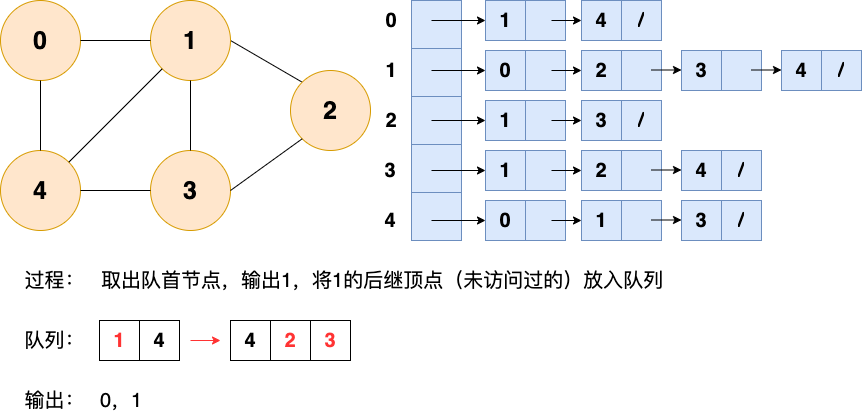
第4步:
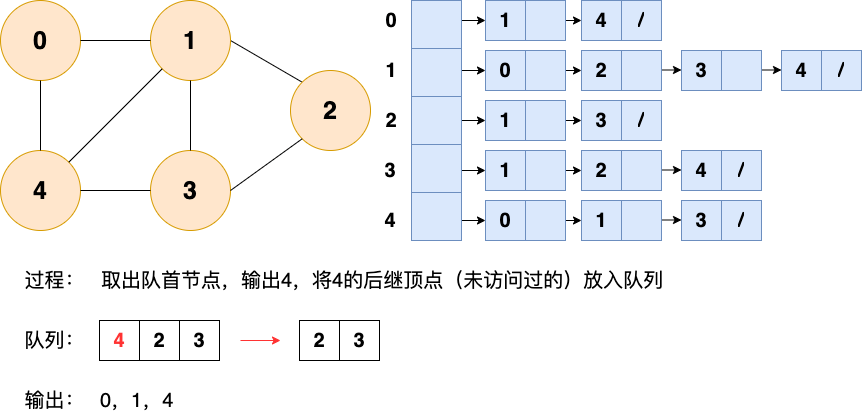
第5步:
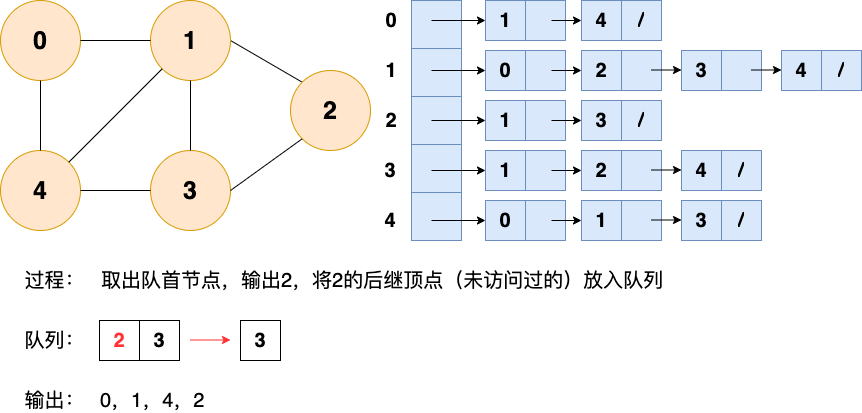
第6步:
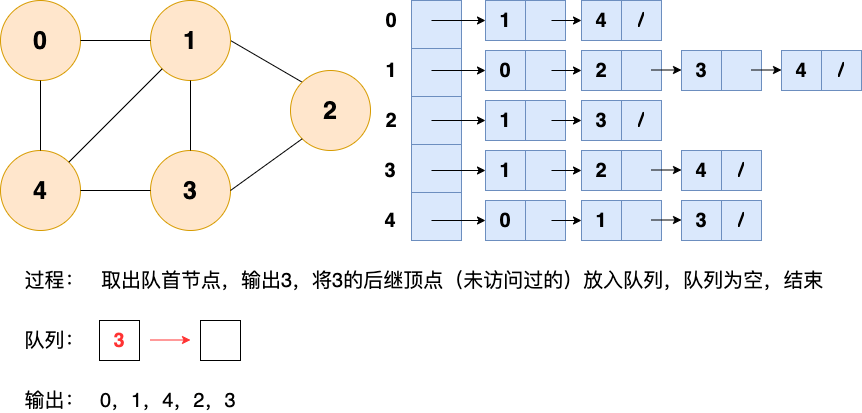
深度優先搜索
深度優先搜索就是“一條路走到黑”,從源頂點開始,一直走到沒有后繼節點,才回溯到上一頂點,然后繼續“一條路走到黑”,如下圖所示:
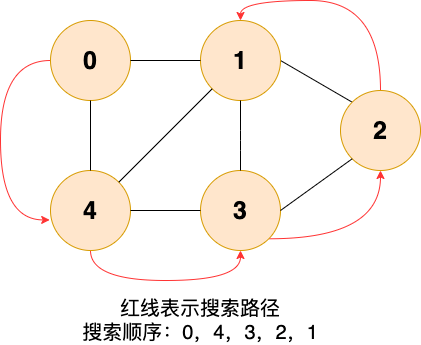
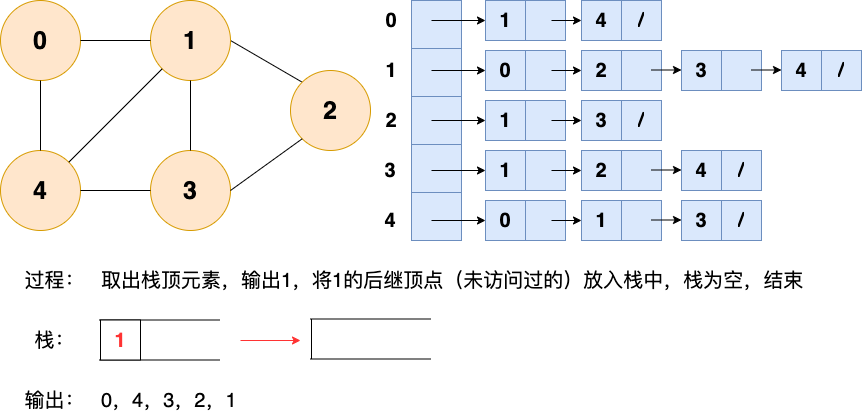
和廣度優先搜索類似,深度優先搜索的具體實現用到了另一種線性數據結構——棧 。具體過程如下圖所示:
第1步:
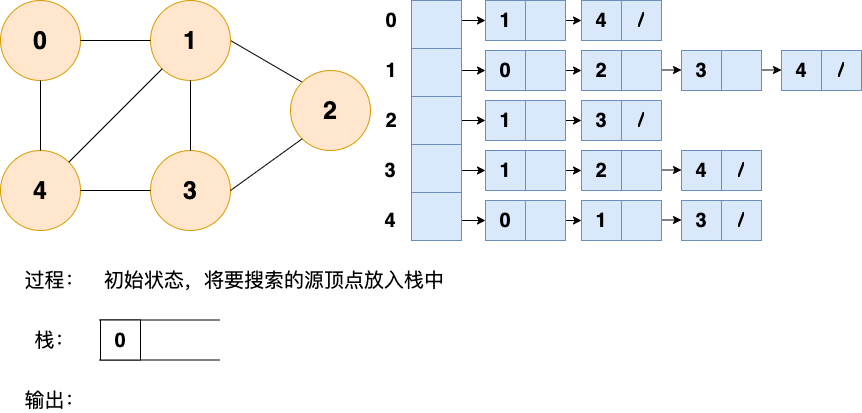
第2步:
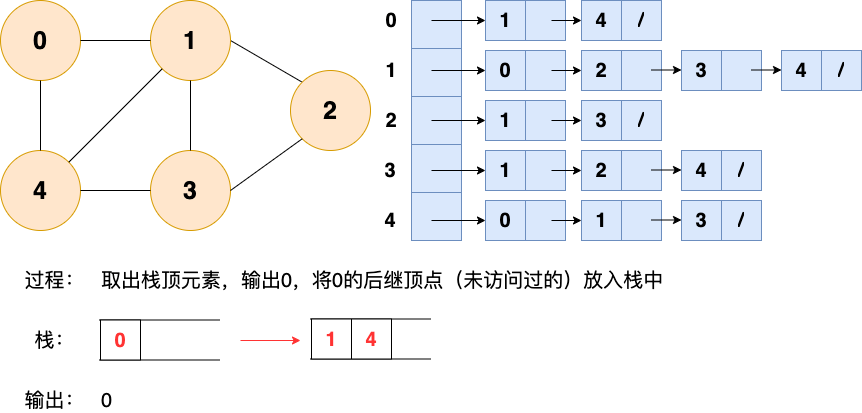
第3步:
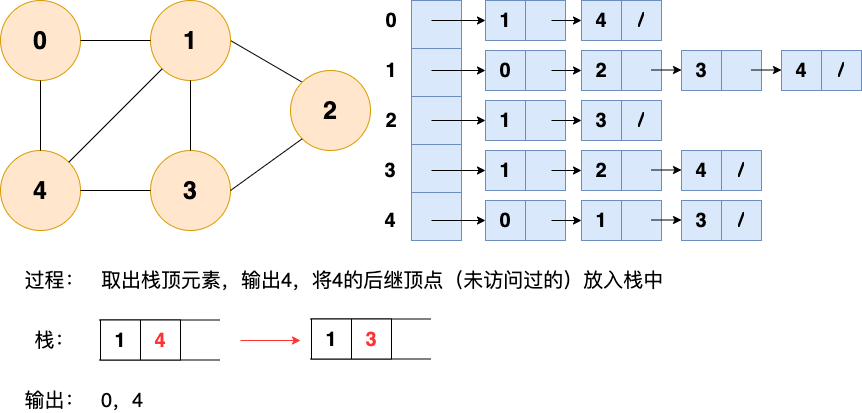
第4步:
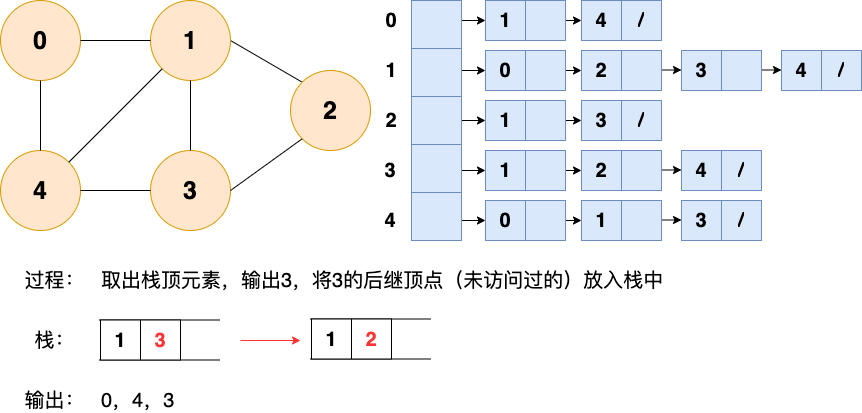
第5步:
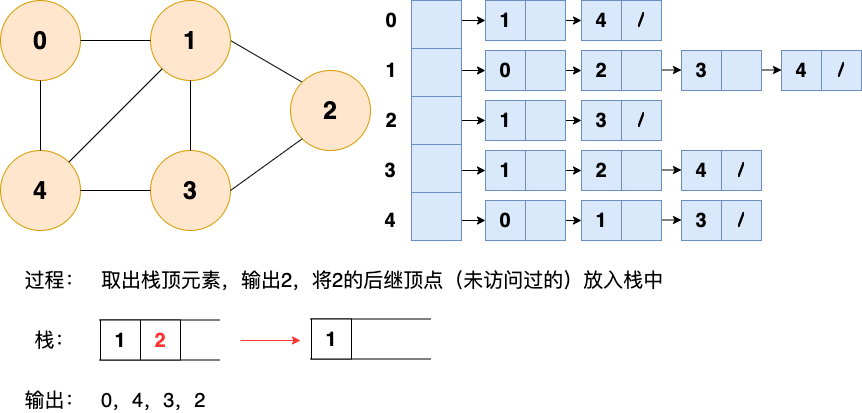
第6步:
堆
什么是堆
堆是一種滿足以下條件的樹:
堆中的每一個節點值都大于等于(或小于等于)子樹中所有節點的值。或者說,任意一個節點的值都大于等于(或小于等于)所有子節點的值。
大家可以把堆(最大堆)理解為一個公司,這個公司很公平,誰能力強誰就當老大,不存在弱的人當老大,老大手底下的人一定不會比他強。這樣有助于理解后續堆的操作。
!!!特別提示:
- 很多博客說堆是完全二叉樹,其實并非如此,堆不一定是完全二叉樹,只是為了方便存儲和索引,我們通常用完全二叉樹的形式來表示堆,事實上,廣為人知的斐波那契堆和二項堆就不是完全二叉樹,它們甚至都不是二叉樹。
- (二叉)堆是一個數組,它可以被看成是一個 近似的完全二叉樹。——《算法導論》第三版
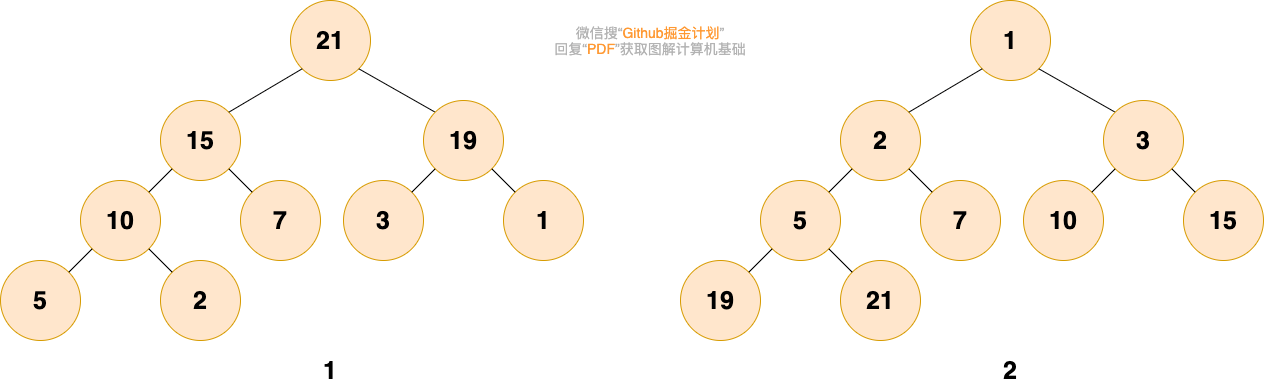
大家可以嘗試判斷下面給出的圖是否是堆?
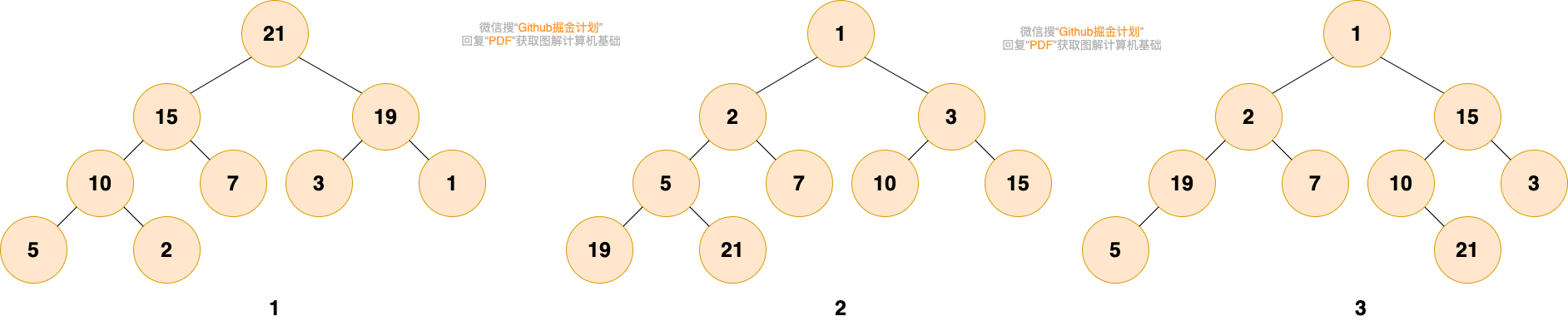
第1個和第2個是堆。第1個是最大堆,每個節點都比子樹中所有節點大。第2個是最小堆,每個節點都比子樹中所有節點小。
第3個不是,第三個中,根結點1比2和15小,而15卻比3大,19比5大,不滿足堆的性質。
堆的用途
當我們只關心所有數據中的最大值或者最小值,存在多次獲取最大值或者最小值,多次插入或刪除數據時,就可以使用堆。
有小伙伴可能會想到用有序數組,初始化一個有序數組時間復雜度是 O(nlog(n)),查找最大值或者最小值時間復雜度都是 O(1),但是,涉及到更新(插入或刪除)數據時,時間復雜度為 O(n),即使是使用復雜度為 O(log(n)) 的二分法找到要插入或者刪除的數據,在移動數據時也需要 O(n) 的時間復雜度。
相對于有序數組而言,堆的主要優勢在于更新數據效率較高。 堆的初始化時間復雜度為 O(nlog(n)),堆可以做到O(1)時間復雜度取出最大值或者最小值,O(log(n))時間復雜度插入或者刪除數據,具體操作在后續章節詳細介紹。
堆的分類
堆分為 最大堆 和 最小堆。二者的區別在于節點的排序方式。
- 最大堆 :堆中的每一個節點的值都大于等于子樹中所有節點的值
- 最小堆 :堆中的每一個節點的值都小于等于子樹中所有節點的值
如下圖所示,圖1是最大堆,圖2是最小堆
堆的存儲
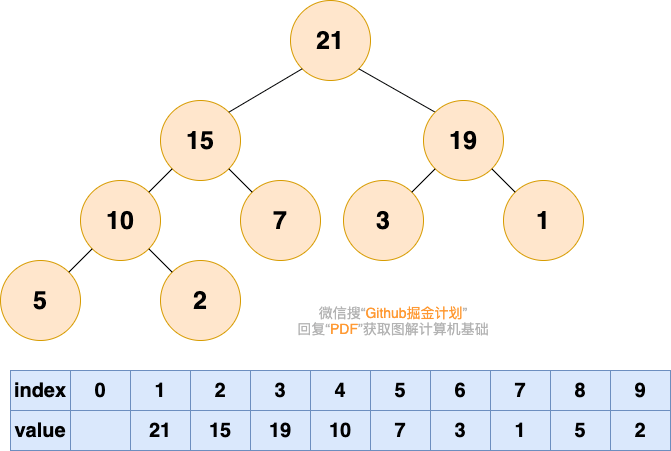
之前介紹樹的時候說過,由于完全二叉樹的優秀性質,利用數組存儲二叉樹即節省空間,又方便索引(若根結點的序號為1,那么對于樹中任意節點i,其左子節點序號為 2*i,右子節點序號為 2*i+1)。
為了方便存儲和索引,(二叉)堆可以用完全二叉樹的形式進行存儲。存儲的方式如下圖所示:
堆的操作
堆的更新操作主要包括兩種 : 插入元素 和 刪除堆頂元素。操作過程需要著重掌握和理解。
在進入正題之前,再重申一遍,堆是一個公平的公司,有能力的人自然會走到與他能力所匹配的位置
插入元素
插入元素,作為一個新入職的員工,初來乍到,這個員工需要從基層做起
1.將要插入的元素放到最后
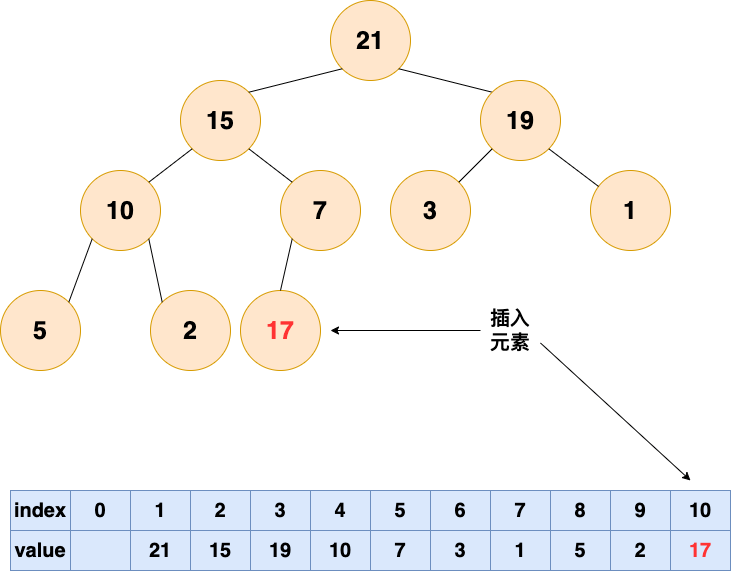
有能力的人會逐漸升職加薪,是金子總會發光的!!!
2.從底向上,如果父結點比該元素大,則該節點和父結點交換,直到無法交換
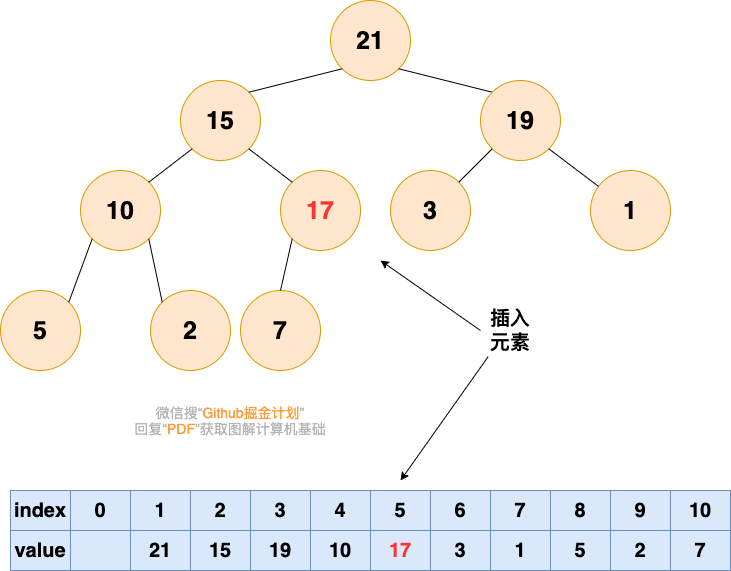
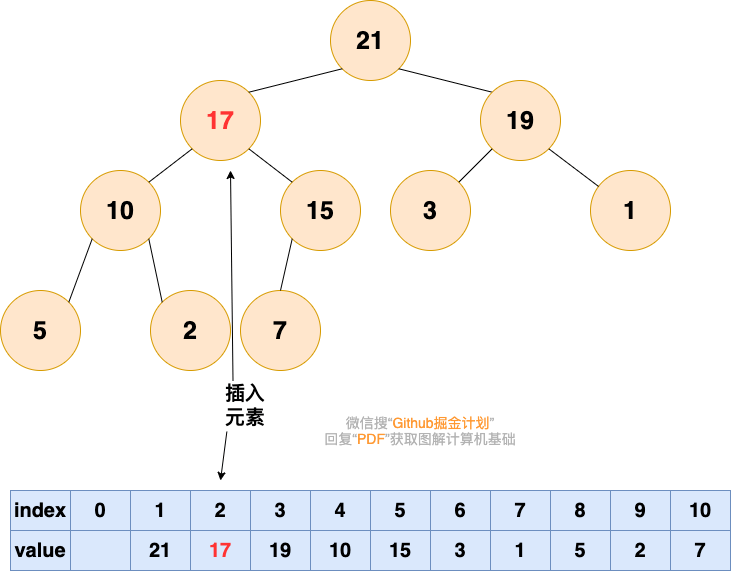
刪除堆頂元素
根據堆的性質可知,最大堆的堆頂元素為所有元素中最大的,最小堆的堆頂元素是所有元素中最小的。當我們需要多次查找最大元素或者最小元素的時候,可以利用堆來實現。
刪除堆頂元素后,為了保持堆的性質,需要對堆的結構進行調整,我們將這個過程稱之為"堆化",堆化的方法分為兩種:
- 一種是自底向上的堆化,上述的插入元素所使用的就是自底向上的堆化,元素從最底部向上移動。
- 另一種是自頂向下堆化,元素由最頂部向下移動。在講解刪除堆頂元素的方法時,我將闡述這兩種操作的過程,大家可以體會一下二者的不同。
自底向上堆化
在堆這個公司中,會出現老大離職的現象,老大離職之后,他的位置就空出來了
首先刪除堆頂元素,使得數組中下標為1的位置空出。
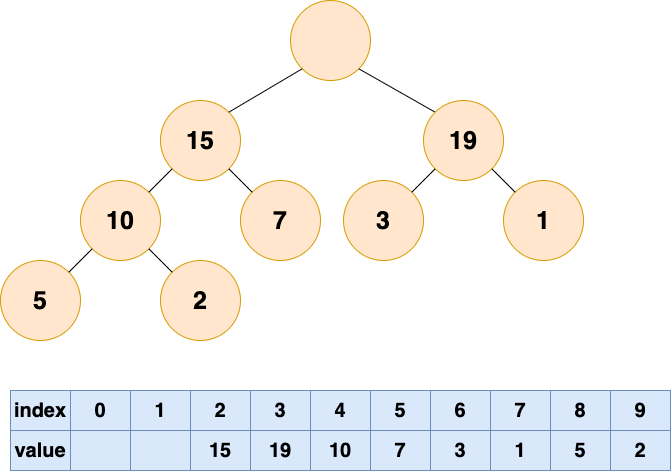
那么他的位置由誰來接替呢,當然是他的直接下屬了,誰能力強就讓誰上唄
比較根結點的左子節點和右子節點,也就是下標為2,3的數組元素,將較大的元素填充到根結點(下標為1)的位置。
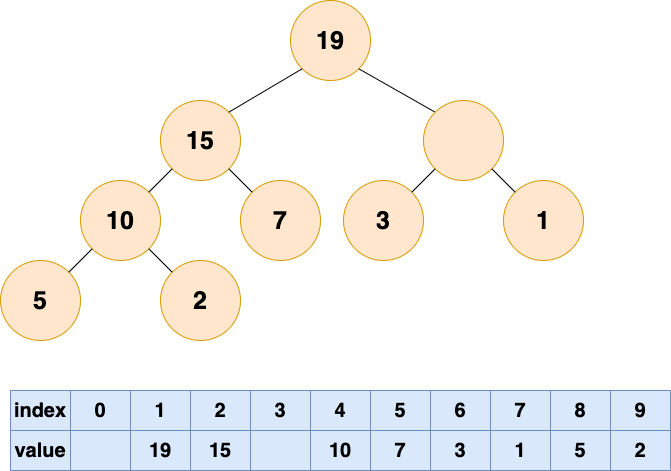
這個時候又空出一個位置了,老規矩,誰有能力誰上
一直循環比較空出位置的左右子節點,并將較大者移至空位,直到堆的最底部
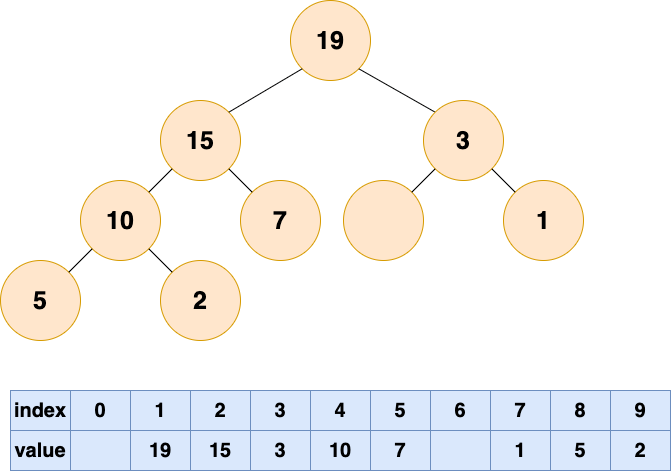
這個時候已經完成了自底向上的堆化,沒有元素可以填補空缺了,但是,我們可以看到數組中出現了“氣泡”,這會導致存儲空間的浪費。接下來我們試試自頂向下堆化。
自頂向下堆化
自頂向下的堆化用一個詞形容就是“石沉大海”,那么第一件事情,就是把石頭抬起來,從海面扔下去。這個石頭就是堆的最后一個元素,我們將最后一個元素移動到堆頂。
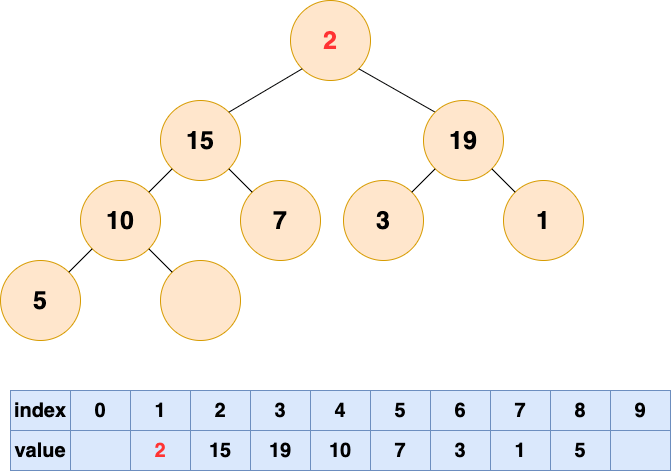
然后開始將這個石頭沉入海底,不停與左右子節點的值進行比較,和較大的子節點交換位置,直到無法交換位置。
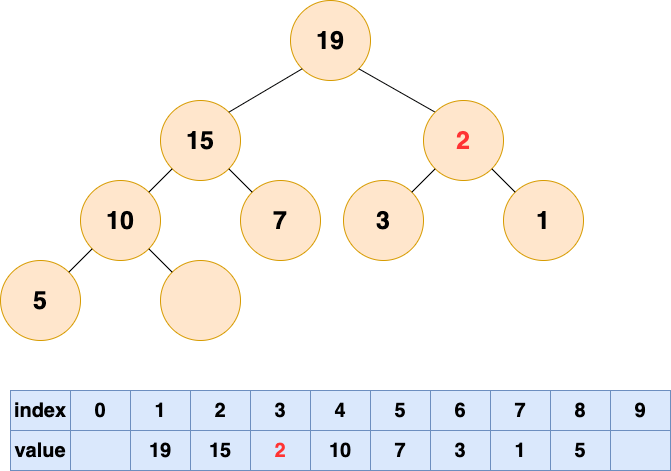
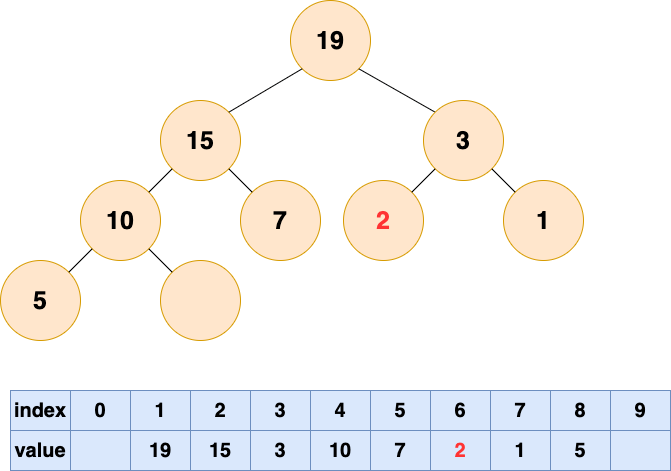
堆的操作總結
- 插入元素 :先將元素放至數組末尾,再自底向上堆化,將末尾元素上浮
- 刪除堆頂元素 :刪除堆頂元素,將末尾元素放至堆頂,再自頂向下堆化,將堆頂元素下沉。也可以自底向上堆化,只是會產生“氣泡”,浪費存儲空間。最好采用自頂向下堆化的方式。
堆排序
堆排序的過程分為兩步:
- 第一步是建堆,將一個無序的數組建立為一個堆
- 第二步是排序,將堆頂元素取出,然后對剩下的元素進行堆化,反復迭代,直到所有元素被取出為止。
建堆
如果你已經足夠了解堆化的過程,那么建堆的過程掌握起來就比較容易了。建堆的過程就是一個對所有非葉節點的自頂向下堆化過程。
首先要了解哪些是非葉節點,最后一個節點的父結點及它之前的元素,都是非葉節點。也就是說,如果節點個數為n,那么我們需要對n/2到1的節點進行自頂向下(沉底)堆化。
具體過程如下圖:
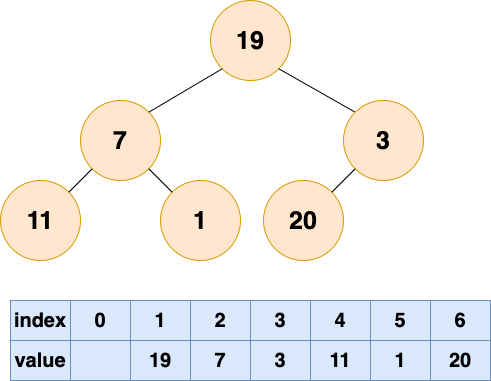
將初始的無序數組抽象為一棵樹,圖中的節點個數為6,所以4,5,6節點為葉節點,1,2,3節點為非葉節點,所以要對1-3號節點進行自頂向下(沉底)堆化,注意,順序是從后往前堆化,從3號節點開始,一直到1號節點。 3號節點堆化結果:
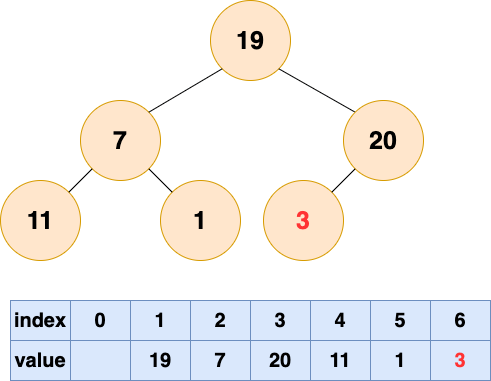
2號節點堆化結果:
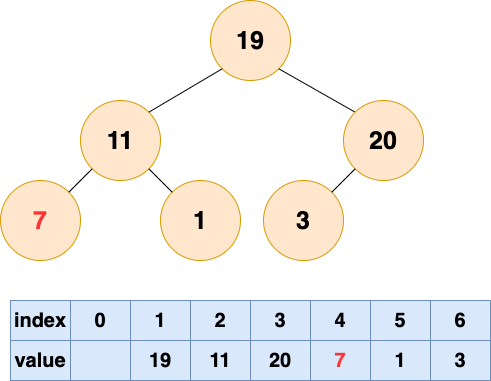
1號節點堆化結果:
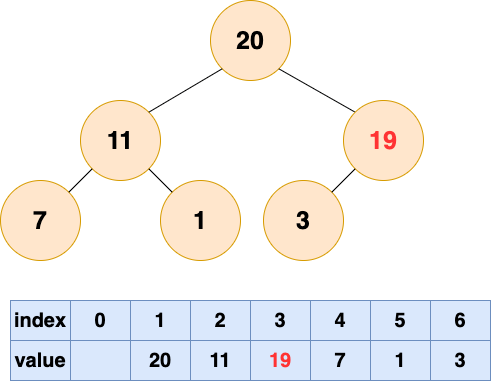
至此,數組所對應的樹已經成為了一個最大堆,建堆完成!
排序
由于堆頂元素是所有元素中最大的,所以我們重復取出堆頂元素,將這個最大的堆頂元素放至數組末尾,并對剩下的元素進行堆化即可。
現在思考兩個問題:
- 刪除堆頂元素后需要執行自頂向下(沉底)堆化還是自底向上(上浮)堆化?
- 取出的堆頂元素存在哪,新建一個數組存?
先回答第一個問題,我們需要執行自頂向下(沉底)堆化,這個堆化一開始要將末尾元素移動至堆頂,這個時候末尾的位置就空出來了,由于堆中元素已經減小,這個位置不會再被使用,所以我們可以將取出的元素放在末尾。
機智的小伙伴已經發現了,這其實是做了一次交換操作,將堆頂和末尾元素調換位置,從而將取出堆頂元素和堆化的第一步(將末尾元素放至根結點位置)進行合并。
詳細過程如下圖所示:
取出第一個元素并堆化:
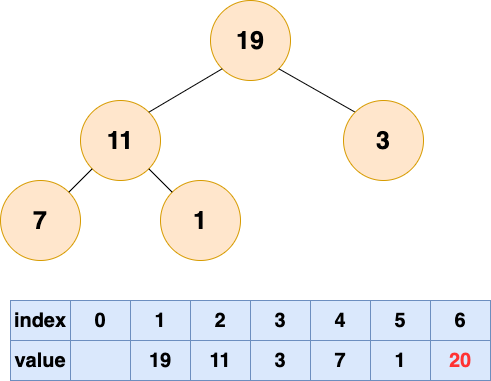
取出第二個元素并堆化:
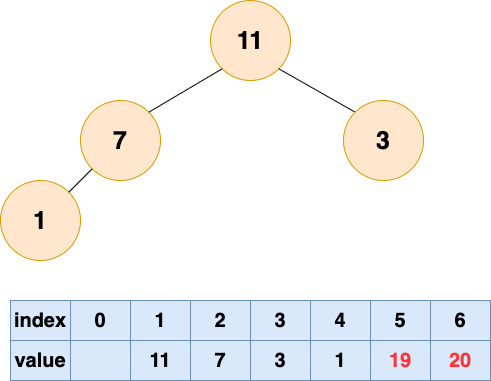
取出第三個元素并堆化:
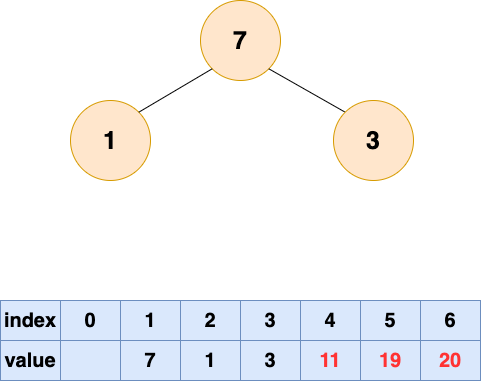
取出第四個元素并堆化:
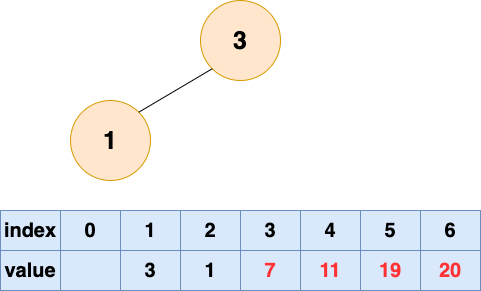
取出第五個元素并堆化:
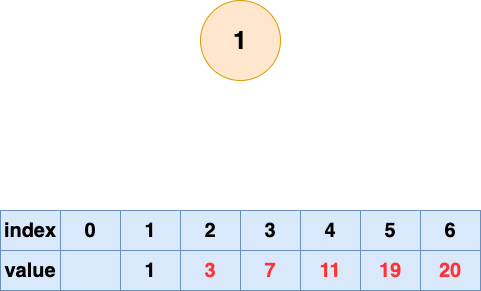
取出第六個元素并堆化:

片轉存中…(img-aSwO5Aie-1640094338369)]
至此,數組所對應的樹已經成為了一個最大堆,建堆完成!
排序
由于堆頂元素是所有元素中最大的,所以我們重復取出堆頂元素,將這個最大的堆頂元素放至數組末尾,并對剩下的元素進行堆化即可。
現在思考兩個問題:
- 刪除堆頂元素后需要執行自頂向下(沉底)堆化還是自底向上(上浮)堆化?
- 取出的堆頂元素存在哪,新建一個數組存?
先回答第一個問題,我們需要執行自頂向下(沉底)堆化,這個堆化一開始要將末尾元素移動至堆頂,這個時候末尾的位置就空出來了,由于堆中元素已經減小,這個位置不會再被使用,所以我們可以將取出的元素放在末尾。
機智的小伙伴已經發現了,這其實是做了一次交換操作,將堆頂和末尾元素調換位置,從而將取出堆頂元素和堆化的第一步(將末尾元素放至根結點位置)進行合并。
詳細過程如下圖所示:
取出第一個元素并堆化:
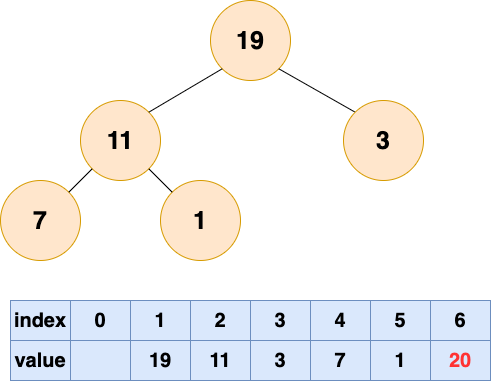
取出第二個元素并堆化:
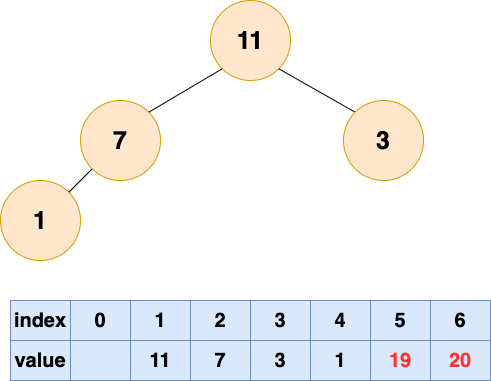
取出第三個元素并堆化:
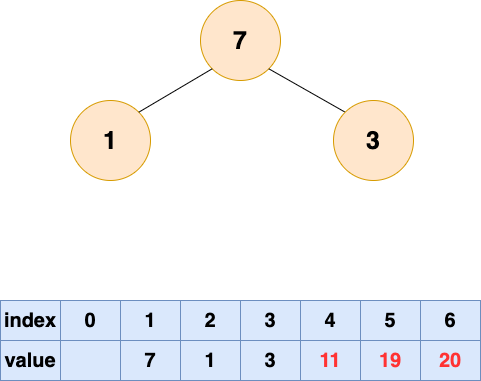
取出第四個元素并堆化:
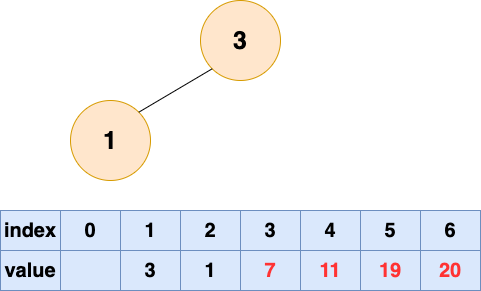
取出第五個元素并堆化:
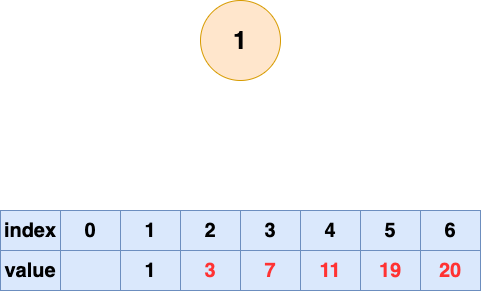
取出第六個元素并堆化:

堆排序完成!




)














