數據結構與算法緒論

基本概念和術語

• 數據

數據是信息的載體，是描述客觀事物屬性的數，字符以及所有能輸入到計算機中并被計算機程序識別和處理的符號的集合。

• 數據元素

數據元素是數據的基本單位，通常作為一個整體進行考慮和處理。一個數據元素可由若干個數據項組成，數據項是構成數據元素的不可分割的最小單位。例如，學生記錄就是一個數據元素，它由學號、姓名、性別等數據項組成。

• 數據對象

數據對象是具有相同性質的數據元素的集合，是數據的一個子集。例如，整數數據對象是集合 \(N = \lbrace 0, \pm 1, \pm 2, \cdots \rbrace\)

• 數據類型

數據類型是一個值的集合和定義在此集合上一組操作的總稱。

（1）原子類型：其值不可再分的數據類型。

（2）結構類型：其值可以再分解為若干成分的數據類型。

（3）抽象數據類型：抽象數據組織和與之相關的操作。

• 抽象數據類型

抽象數據類型是指一個數學模型以及定義在該模型上的一組操作。抽象數據類型的定義僅取決于它的一組邏輯特性，而與其在計算機內部如何表示和實現無關，即不論其內部結構如何變化，只要它的數學特性不變，都有不影響其外部的使用。通常用（數據對象、數據關系、基本操作集）這樣的三元組來表示抽象數據類型。

• 數據結構

在任何問題中，數據元素都不是孤立存在的，而是在它們之間存在著某種關系，這種數據元素相互之間的關系稱為結構。數據結構是相互之間存在的一種或多種特定關系的數據元素集合。數據結構包括三方面的內容：邏輯結構、存儲結構和數據的運算。數據的邏輯結構和存儲結構時密不可分的兩個方面，一個算法的設計取決于所選定的邏輯結構，而算法的實現依賴于所采用的存儲結構。

數據的邏輯結構

邏輯結構是指數據元素之間的邏輯關系，即從邏輯關系上描述數據。它與數據的存儲無關，是獨立于計算機的。

劃分方法一

（1）線性結構

有且僅有一個開始和一個終端結點，并且所有結點都最多只有一個直接前趨和一個后繼。

例如：線性表、棧、隊列、串

（2）非線性結構

一個結點可能有多個直接前趨和直接后繼。

例如：樹、圖

劃分方法二

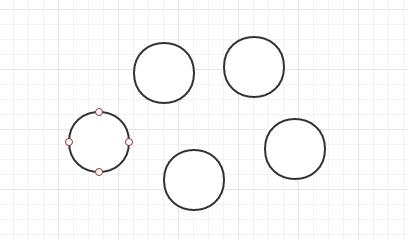
集合

• 數據元素間除“同屬于一個集合”外，無其它關系

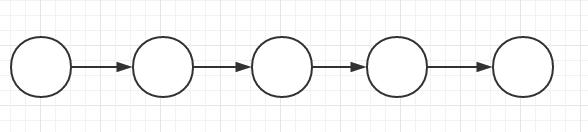
線性結構

• 一個對一個，如線性表、棧、隊列

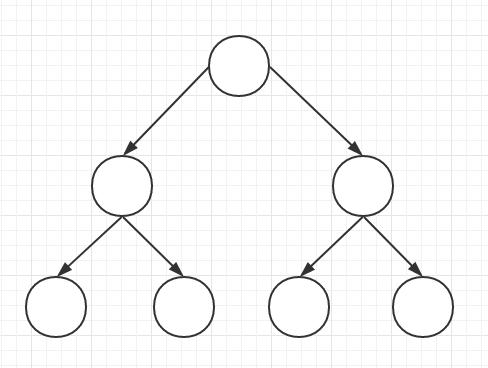
樹形結構

• 一個對多個，如樹

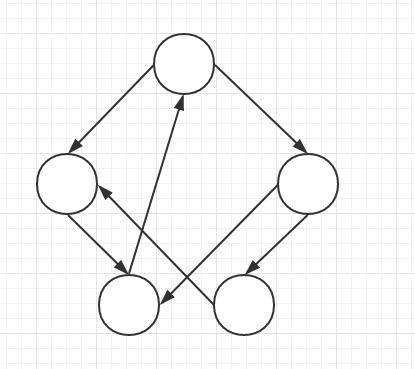
圖形結構

• 多個對多個，如圖

數據的存儲結構

存儲結構是指數據結構在計算機中的表示（又稱映像），也稱物理結構。它包括數據元素的表示和關系的表示。數據的存儲結構是邏輯結構用計算機語言的實現，它依賴于計算機語言。數據的存儲結構主要有：順序存儲、鏈式存儲、索引存儲和散列存儲。

• （1）順序存儲：把邏輯上相鄰的元素存儲在物理位置上也相鄰的存儲單元里，元素之間的關系有存儲單元的鄰接關系來體現。其優點是可以實現隨機存取，每個元素占用最少的存儲空間；缺點是只能使用相鄰的一整塊存儲單元，因此可能產生較多的外部碎片。
• （2）鏈接存儲：不要求邏輯上相鄰的元素在物理位置上也相鄰，借助指示元素存儲地址的指針表示元素之間的邏輯關系。其優點是不會出現碎片現象，充分利用所有存儲單元；缺點是每個元素因存儲指針而占用額外的存儲空間，并且只能實現順序存儲。
• （3）索引存儲：在存儲元素信息的同時，還建立附加的索引表。索引表中的每一項稱為索引項，索引項的一般形式是：（關鍵字，地址）。其優點是檢索速度快；缺點是增加了附加的索引表，會占用較多的存儲空間。另外，在增加和刪除數據時要修改索引表，因而會花費較多額時間。
• （4）散列結構：根據元素的關鍵字直接計算出該元素的存儲地址，又稱為 Hash 存儲。其優點是檢索、增加和刪除結點的操作都很快；缺點是如果散列函數不好可能出現元素存儲單元的沖突，而解決沖突會增加時間和空間開銷。

注：

數據的邏輯結構是以面向實際問題的角度出發的，只采用抽象表達方式，獨立于存儲結構，數據的存儲方式有多種不同的選擇；而數據的存儲結構是邏輯結構在計算機上的映射，它不能獨立于邏輯結構而存在。數據結構包括三要素，缺一不可。

算法的特性

算法是對特定問題求解步驟的一種描述，它是指令的有限序列，其中每一條指令表示一個或多個操作。此外，一個算法還具有下列 5 個重要特性。

（1）有窮性: 一個算法必須總是（對任何合法的輸入值）在執行有窮步之后結束，且每一步都可在有窮時間內完成。

（2）確定性: 算法中每一條指令必須有確切的含義，讀者理解時不會產生二義性。即對于相對的輸入只能得出相同的輸出。

（3）可行性: 一個算法是可行的，即算法中描述的操作都是可以通過已經實現的基本運算執行有限次來實現的。

（4）輸入 : 一個算法有零個或者多個的輸入，這些輸入取自于每個特定的對象的集合。

（5）輸出 : 一個算法有一個或者多個輸出，這些輸出是同輸入有著某種特定關系的量。

通常設計一個“好”的算法應考慮達到以下目標。

（1）正確性：算法應當能夠正確地解決求解問題。

（2）可讀性：算法應當具有良好的可讀性，以助于人民理解。

（3）健壯性：當輸入非法數據時，算法也能適當地做出反應或進行處理，而不會產生莫名其妙的輸出結果。

（4）效率與低存儲量需求：效率是指算法執行的時間，存儲量需求是指算法執行過程中所需要的最大存儲空間，
這兩者都與問題的規模有關。

算法效率的度量

算法效率的度量是通過時間復雜度和空間復雜度來描述的。

1、時間復雜度

一個語句的頻度是指該語句在算法中被重復執行的次數。算法中所有語句的頻度之和記作 \(T(n)\)，它是該算法問題規模 n 的函數，時間復雜度主要分析 \(T(n)\) 的數量級。算法中的基本運算的頻度與\(T(n)\)同數量級，所以通常采用算法中基本運算的頻度 \(f(n)\) 來分析算法的時間復雜度。因此，算法的時間復雜度記為：\(T(n)=O(f(n))\)

上式中 O 的含義是 \(T(n)\) 的數量級，其嚴格的數學定義是：若 \(T(n)\) 和 \(f(n)\) 是定義在正整數集合上的兩個函數，則存在正常數 \(C\) 和 \(n_0\) ，使得\(n>=n_0\)時，都滿足 \(\color{red}{0<=T(n)<=C*f(n)}\) 。其中 \(f(n)\) 是 \(T(n)\) 的一個漸近函數。

算法的時間復雜度不僅依賴于問題的規模 n，也取決于待輸入數據的性質。

例如 在數組 \(A[0, \cdots, n-1]\) 中，查找定值 k 的算法大致如下：

i = n - 1;
while(i>=0 && (A[i] != k))i--;
return i;

此算法中的語句（3）（基本運算）的頻度不僅與問題規模有關，還與輸入實例中 A 的各元素取值及 k 的取值有關：

（1）若 A 中沒有與 k 相等的元素，則語句（3）的頻度\(f(n) =n\)。

（2）若 A 中的最有一個元素等于 k，則語句（3）的頻度\(f(n)\) 是常數 0。

最壞時間復雜度是指在最壞情況下，算法的時間復雜度。

平均時間復雜度是指所有可能輸入實例在等概率出現的情況下，算法的期望運行時間。

最好時間復雜度是指在最好情況下，算法的時間復雜度。

一般總是考慮在最壞情況下的時間復雜度，以保證算法的運行時間不會比它更長。

在分析一個程序的時間復雜性時，有以下兩條規則：

• 加法規則

\(T(n)=T1(n)+T2(n)=O(f(n))+O(g(x))=O(max(f(n),g(n)))\)

• 乘法規則

\(T(n)=T1(n) \times T2(n)=O(f(n)) \times O(g(x))=O(f(n) \times g(n))\)

常見的漸近時間復雜度

• 常量復雜度 \(O(1)\)
• 對數復雜度 \(O(logn)\)
• 線性復雜度 \(O(n)\)
• 平方復雜度 \(O(n^2)\)
• 指數復雜度 \(O(2^n)\)

基本的復雜度如上，基于以上的表達式可以有很多的組合，其中 \(logn\) 默認情況下等同于 \(log_{2}n\)

大小關系：

\(O(1) < O(log_2n) < O(n) < O(nlog_2n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)\)

2、空間復雜度

算法的空間復雜度\(S（n）\)定義為該算法所耗費的存儲空間，它是問題的規模\(n\)的函數。漸進空間復雜度簡稱為空間復雜度，記作\(S（n）=O（g（n））\)。

一個上機程序除了需要存儲空間來存放本身所用指令、常數、變量和輸入數據外，也需要一些對數據進行操作的工作單位和存儲一些為實現計算所需信息的輔助空間，若輸入數據所占空間只取決于問題本身，和算法無關，組只需分析輸入和程序之外的額外空間了。

算法原地工作是指算法所需輔助空間是常量，即\(O（1）\)。

算法復雜的意義

算法復雜度的分級相當于（高等數學）的無窮大的階，反映了在規模\(n\)趨于無窮大的過程中，算法代價增長的速度。算法的復雜度越高，其實施的代價隨著規模增大而增長的速度越快。

\(example\)

\(斐波那契數列的第n項\)

• 遞歸算法

def fib(n):if n < 2:return 1else:return fib(n-1) + fib(n-2)

將參數\(n\)看問題實例的規模，不難看出，計算\(F_n\)的時間代價（考慮求加法操作的次數）大致等于計算\(F_{n-1}\)和\(F_{n-2}\) 的時間代價之和。這一情況說明，計算\(F_n\)的時間代價大致等比于斐波那契數\(F_n\)的值。根據已有的結論：

\[ \mathop {\lim }\limits_{n \to \infty } {F_n} = {(\frac{{\sqrt 5 + 1}}{2})^n}=1.618^n \]

可以看到計算\(F_n\)的時間代價按\(n\)值的指數增長。

• 遞推算法

def fib(n):f1 = f2 = 1for k in range(1,n):f1, f2 = f2, f2 + f1return f2

用這個算法計算\(F_n\)的值，循環的工作只做一次，循環需要做\(n-1\)次。每次循環中只執行了幾個簡單動作，總的工作量（基本操作執行次數）與\(n\)值呈現某種線性關系。

這個例子說明，解決同一問題的不同算法，其計算復雜度的差異很大，甚至具有截然不同的性質。通過分析算法復雜度，可以幫助使用者選擇適用的算法；也可能發現已知算法的缺陷，促使人們設法開發更好的算法 。

Python 內置類型性能分析

timeit 模塊

timeit 模塊可以用來測試一小段 Python 代碼的執行速度。

class timeit.Timer(stmt='pass', setup='pass', timer=<timer function>)

Timer 是測量小段代碼執行速度的類。

stmt 參數是要測試的代碼語句（statment）；

setup 參數是運行代碼時需要的設置；

timer 參數是一個定時器函數，與平臺有關。

timeit.Timer.timeit(number=1000000)

Timer 類中測試語句執行速度的對象方法。number 參數是測試代碼時的測試次數，默認為 1000000 次。方法返回執行代碼的平均耗時，一個 float 類型的秒數。

list 的操作測試

def test1():l = []for i in range(1000):l = l + [i]
def test2():l = []for i in range(1000):l.append(i)
def test3():l = [i for i in range(1000)]
def test4():l = list(range(1000))from timeit import Timert1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "seconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "seconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "seconds")# ('concat ', 1.7890608310699463, 'seconds')
# ('append ', 0.13796091079711914, 'seconds')
# ('comprehension ', 0.05671119689941406, 'seconds')
# ('list range ', 0.014147043228149414, 'seconds')

pop 操作測試

x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")pop_zero = Timer("x.pop(0)","from __main__ import x")pop_zero = Timer("x.pop(0)","from __main__ import x")pop_zero = Timer("x.pop(0)","from __main__ import x")pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')

測試 pop 操作：從結果可以看出，pop 最后一個元素的效率遠遠高于 pop 第一個元素

list 內置操作的時間復雜度

\[ \begin{array}{lc} Op & O \ Efficiency \\ indexx[\ ] & O(1) \\ index \ assignment & O(1) \\ append & O(1) \\ pop() & O(1) \\ pop(i) & O(n) \\ insert(i, item) & O(n) \\ del \ operator & O(n) \\ iteration & O(n) \\ contain(in) & O(n) \\ get \ slice[x:y] & O(k) \\ del \ slice & O(n) \\ set \ slice & O(n+k) \\ reverse & O(n) \\ concatenate & O(k) \\ sort & O(nlogn) \\ multiply & O(nk) \\ \end{array} \]

從上可以看出 list 大概是順序表實現。

dict 內置操作的時間復雜度

\[ \begin{array}{lc} Op & O \ Efficiency \\ copy & O(1) \\ get \ item & O(1) \\ set \ item & O(1) \\ del \ item & O(1) \\ contains(in) & O(1) \\ iteration & O(n) \\ \end{array} \]