數據結構與算法-ADT-Array

Array ADT

一維數組是連續元素的集合，其中的每個元素都可以通過唯一的整數下標來存取。數組的大小在創建后不能修改。

ADT 定義：

Array(size): 創建一個長度為 size 的一維數組，并且將每個元素初始化成 None
length(): 返回數組中的元素個數
getitem(index): 返回指定下標的元素
setitem(index, value): 修改數組中 index 位置的元素值
clearing(value): 將數組中的所有元素值重置成 value
iterator(): 返回迭代器

Array 的實現

ctypes 模塊

Python 中的許多數據類型及類實際上都是基于低層 C 語言中的相關類型實現的。Python 標準庫中的 ctypes 模塊可用來訪問 C 語言中的各種類型及 C 類庫中的功能。使用 ctypes 提供的大多數功能都要求理解一些 C 語言知識。

類似 Python 實現 string, list, tuple 和 dict，我們通過 ctypes 創建一個數組，其中的元素都是 Python 對象引用：

for i in range(5):slots[i] = None

這個數組必須先初始化后才能訪問，不然會拋出異常，如 slots[0] 會拋出異常，初始化如下：

import ctypesclass Array:def __init__( self, size ):assert size > 0, "Array size must be > 0"self._size = sizePyArrayType = ctypes.py_object * sizeself._elements = PyArrayType()self.clear( None )def __len__( self ):return self._sizedef __getitem__( self, index ):assert index >= 0 and index < len(self), "Array subscript out of range"return self._elements[ index ]def __setitem__( self, index, val ):assert index >= 0 and index < len(self), "Array subscript out of range"self._elements[ index ] = valdef clear( self, val ):for i in xrange( self._size ):self._elements[ i ] = valdef __iter__( self ):return _ArrayGenerator( self._elements, self._size )def _ArrayGenerator( elements, size ):for i in range( size ):yield elements[i]

Array 的實現如下：

pyList = [4, 12, 2, 34, 17]

Python List

Python List 也是通過低層的 C 語言類型實現的，它是一個可修改的序列容器，其大小可以隨著元素的添加和刪除自動改變。

創建一個 Python List

pyListA = [34, 12]
pyListB = [4, 6, 31, 9]
pyListA.extend(pyListB)

以上代碼將調用 list() 構造器，構造器將創建一個數組結構用來存儲列表中的元素。實際上初始創建的數組大小會大于所需的容量，這樣便于以后的擴展操作。

用于存儲列表元素的數組實際上是剛才創建的數組中的一個子數組 subarray。len(lst) 返回該子數組的長度，而整個數組的長度為 capacity。用數組實現的 Python List 的抽象和物理視圖如下：

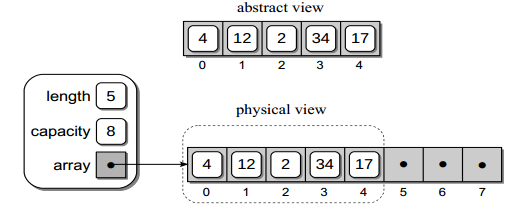
追加元素 append

當數組容量足夠時，新元素將追加到數組中，并且 list 的 length 域也相應增加。

當數組満時，List 會進行自動擴展，即：

新建一個更大容量的數組
將原數組的元素全部復制到新建的數組
將新建的數組設置為 List 的數據結構
銷毀舊的數組

新建數組的大小是根據原數組的大小確定的，比如說，新數組的大小定為原數組大小的 2 倍。擴展后再在數組后追加元素。

擴充列表 extend

比如：

pyList.insert(3, 79)

當 pyListA 中的數組容量不夠時，List 會自動進行如 append 進行的類似數組擴展操作。

插入 insert

比如：

pyList.pop(0) # remove the first item
pyList.pop() # remove the last item

當位置 3 已經有元素時，位置 3 及其后面的所有元素都將后移一個位置，并在位置 3 插入新元素。當數組容器不夠，會進行和上面相似的數組擴展操作。

刪除 pop

比如：

class Array2D:def __init__( self, nrows, ncols ):# Create a 1-D array to store an array reference for each row.self._theRows = Array( nrows )# Create the 1-D arrays for each row of the 2-D array.for i in range( nrows ):self._theRows[i] = Array( ncols )def numRows( self ):return len( self._theRows )def numCols( self ):return len( self._theRows[0] )# Clears the array by setting every element to the given value.def clear( self, val ):for row in range( self.numRows() ):self._theRows[row].clear( val )def __getitem__( self, xy ):assert len( xy ) == 2, "Invalid number of array subscripts."row = xy[0]col = xy[1]assert row >= 0 and row < self.numRows() and \col >= 0 and col < self.numCols(), "Array subscript out of range."the1arr = self._theRows[row]return the1arr[col]def __setitem__( self, xy, val ):assert len( xy ) == 2, "Invalid number of array subscripts."row = xy[0]col = xy[1]assert row >= 0 and row < self.numRows() and \col >= 0 and col < self.numCols(), "Array subscript out of range."the1arr = self._theRows[row]the1arr[col] = val

刪除后，如果后面還有元素，那么被刪除元素后面的所有元素將前移一個位置，以便填充刪除后的空位。

當然，如果刪除后的數組空位過多，也會進行相對應的收縮數組操作。

List Slice

Slice 會創建一個新的 List。

二維數組 two-dimensional array

它將數據組織成行和列，類似于表格。每個元素通過兩個下標來存取。

Array2D ADT

Array2D(nrows, ncols): 創建一個 nrows 行，ncols 列的二維數組，并初始化每個元素為 None
numRows(): 返回行數
numCols(): 返回列數
clear(value): 將所有元素的值設為 value
getitem(row, col): 通過下標法 y=x[1,2] 來訪問元素
setitem(row, col, value): 設置元素值

Array2D 的實現

通常有 2 種數據組織方法：

使用一個一維數組，將行列上的每個元素位置映射到數組的相應位置
使用數組的數組實現

下面的實現采用了數組的數組方法，將二維數組中的每一行存儲在一維數組中，然后再創建一個數組，用來保存行數組（即該數組是數組的數組）。Array2D 的抽象和物理存儲視圖如下：

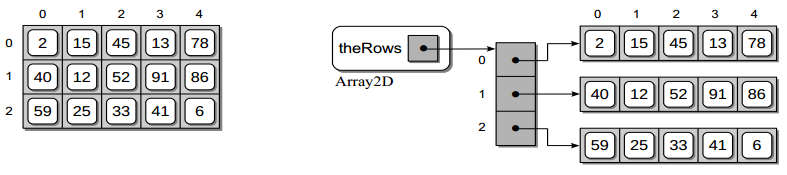
有些語言的實現中，可以存取每個行，從而對每個元素的訪問使用 x[r][c] 進行。為了隱藏實現細節，我們的實現不暴露行數組，從而對每個元素的訪問使用 x[r,c] 進行。

實現如下：

class Array2D:def __init__( self, nrows, ncols ):# Create a 1-D array to store an array reference for each row.self._theRows = Array( nrows )# Create the 1-D arrays for each row of the 2-D array.for i in range( nrows ):self._theRows[i] = Array( ncols )def numRows( self ):return len( self._theRows )def numCols( self ):return len( self._theRows[0] )# Clears the array by setting every element to the given value.def clear( self, val ):for row in range( self.numRows() ):self._theRows[row].clear( val )def __getitem__( self, xy ):assert len( xy ) == 2, "Invalid number of array subscripts."row = xy[0]col = xy[1]assert row >= 0 and row < self.numRows() and \col >= 0 and col < self.numCols(), "Array subscript out of range."the1arr = self._theRows[row]return the1arr[col]def __setitem__( self, xy, val ):assert len( xy ) == 2, "Invalid number of array subscripts."row = xy[0]col = xy[1]assert row >= 0 and row < self.numRows() and \col >= 0 and col < self.numCols(), "Array subscript out of range."the1arr = self._theRows[row]the1arr[col] = val

實現元素的存取

__getitem__(self, index) 和 __setitem__(self, index. value) 這兩個函數定義參數中，只有一個 index 參數，但這不會限制只能使用一個下標。當使用多個下標時，如 y = x[i,j]，多個下標會組合成一個 tuple 作為 index 參數傳入。

Matrix ADT

矩陣是標量值的集合，這些值以行和列的形式組織成一個固定大小的矩形網格中。

Matrix(nrows, ncols): 創建一個 nrows 行和 ncols 列的矩陣
numRows(): 返回行數
numCols(): 返回列數
getitem(row, col): 返回元素
setitem(row, col, scalar): 設置元素值
scaleBy(scalar): 矩陣中的每個元素都乘該值，操作后矩陣本身將被修改
transpose(): 返回一個轉置矩陣
add(rhsMatrix): 創建并返回一個新矩陣。這兩個矩陣大小必須相同
subtract(rhsMatrix): 相減
multiply(rhsMatrix): 相乘。

Matrix 的實現

一般用二維數組來實現矩陣。

實現如下：

from array import Array2Dclass Matrix:def __init__( self, nrow, ncols ):self._theGrid = Array2D( nrow, ncols )self._theGrid.clear( 0 )def numRows( self ):return self._theGrid.numRows()def numCols( self ):return self._theGrid.numCols()def __getitem__( self, xy ):return self._theGrid[ xy[0], xy[1] ]def __setitem__( self, xy, scalar ):self._theGrid[ xy[0], xy[1] ] = scalardef scaleBy( self, scalar ):for r in xrange( self.numRows() ):for c in xrange( self.numCols() ):self[r, c] *= scalardef transpose( self ):newMatrix = Matrix( self.numCols(), self.numRows() )for r in xrange( self.numRows() ):for c in xrange( self.numCols() ):newMatrix[c, r] = self[r, c]return newMatrixdef add( self, rhsMatrix ):assert rhsMatrix.numRows() == self.numRows() and \rhsMatrix.numCols() == self.numCols(), \"Matrix sizes not compatible for the add operation."newMatrix = Matrix( self.numRows(), self.numCols() )for r in xrange( self.numRows() ):for c in xrange( self.numCols() ):newMatrix[r, c] = self[r, c] + rhsMatrix[r, c]return newMatrixdef subtract( self, rhsMatrix ):assert rhsMatrix.numRows() == self.numRows() and \rhsMatrix.numCols() == self.numCols(), \"Matrix sizes not compatible for the add operation."newMatrix = Matrix( self.numRows(), self.numCols() )for r in xrange( self.numRows() ):for c in xrange( self.numCols() ):newMatrix[r, c] = self[r, c] - rhsMatrix[r, c]return newMatrixdef multiple( self, rhsMatrix ):assert self.numCols() == rhsMatrix.numRows(), \"Matrix sizes not compatible for the multiple operation."newMatrix = Matrix( self.numRows(), rhsMatrix.numCols() )for r in xrange( self.numRows() ):for rhsC in xrange ( rhsMatrix.numCols() ):tmp = 0for c in xrange( self.numCols() ):tmp += self[r, c] * rhsMatrix[c, r]newMatrix[r, rhsC] = tmpreturn newMatrix

應用：游戲人生

The game of Life 是由英國數學家 John H. Conway 發明的，它能模擬生物群落的興衰更替。該游戲可用來觀察一個復雜的系統或模式如何能從一組簡單的規則演化而來。

游戲規則

該游戲使用一個不限大小的矩形網格，其中的每個單元格要么是空的，要么被一個有機體占據。被占據的單元格被視作是活的，而空的單元格被視作是死的。游戲的每次演進，都會基于當前的單元格布局，創造新的“一代”。下一代中的每個單元格狀態是根據以下規則確定的：

若某單元格是活的，并且有 2 或 3 個活的鄰居，那么它在下一代也保持活。每個單元格有 8 個鄰居。
若某單元格是活的，但它沒有活的鄰居，或只有一個活鄰居，它在下一代會死于孤立。
一個活單元格，若有 4 個或更多個活鄰居，它在下一代會死于人口過剩。
一個死單元格，當且僅當只有 3 個活鄰居時，會在下一代重生。

用戶先初始化配置，即指定哪些單元格是活的，然后運用以上的規則，生成下一代。可以看到，一些系統可能最終會消亡，而有些最終會進化成 “穩定” 狀態。例如：

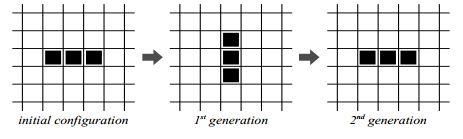
設計方案

一個網格 life grid 用來表示和存儲游戲區。網格包含一組矩形單元格，并分成有限大小的行和列。

LifeGrid(nrows, ncols): 創建一個新的游戲網格。所有單元格設置為空（死）。
numRows(): 返回網格行數。
numCols(): 返回網格列數。
configure(coordList): 配置網格以進行下一代的演化。參數是一個 (row, col) 的序列，每一個元組表示該位置的單元格是活的。
clearCell(row, col): 設置單元格為空（死）。
setCell(row, col): 設置單元格為活。
isLiveCell(row, col): 返回一個布爾值，表示某個單元格是否包含一個活的有機體。
numLiveNeighbors(row, col): 返回某個單元格的所有活鄰居個數。對于邊緣的單元格，落在邊緣外的鄰居都認為是死的。

實現

使用一個二維數組來表示網格。每個單元格的狀態使用 0 和 1 表示，0 表示死，1 表示活。這樣在統計單元格的活鄰居總數時，只需要將鄰居的狀態相加即可。實現時網格的大小是限定的，如果大小超出了，在運行過程中可以重新創建一個新的網格。

# life.py
from array import Array2Dclass LifeGrid:DEAD_CELL = 0LIVE_CELL = 1def __init__( self, nrows, ncols ):self._grid = Array2D( nrows, ncols )self.configure( list() )def numRows( self ):return self._grid.numRows()def numCols( self ):return self._grid.numCols()def configure( self, coordList ):for i in range( self.numRows() ):for j in range( self.numCols() ):self.clearCell(i, j)for coord in coordList:self.setCell( coord[0], coord[1] )def isLiveCell( self, row, col ):return self._grid[ row, col ] == LifeGrid.LIVE_CELLdef clearCell( self, row, col ):self._grid[ row, col ] = LifeGrid.DEAD_CELLdef setCell( self, row, col ):self._grid[ row, col ] = LifeGrid.LIVE_CELLdef numLiveNeighbors( self, row, col ):nrows = self.numRows()ncols = self.numCols()liveNum = 0for i in range( row-1, row+2 ):for j in range( col-1, col+2 ):if ( 0 <= i < nrows ) and ( 0 <= j < ncols ):liveNum += self._grid[i, j]liveNum -= self._grid[ row, col ]return liveNumfrom life import LifeGrid# Define the initial configuration of live cells.
INIT_CONFIG = [ (0, 0), (0, 1), (1, 0), (1, 2), (3, 2), (3, 4), (5, 4), (5, 6), (7, 6), (7, 8), (9, 8), (9, 10), (11, 10), (11, 12), (12, 11), (12, 12)]# Indicate the number of generations
#NUM_GENS = 8def main():GRID_WIDTH = int( raw_input( "Grid width:" ) )GRID_HEIGHT = int( raw_input( "Grid height:" ) )NUM_GENS = int( raw_input( "Nbr of generations to evolve:" ) )grid = LifeGrid( GRID_WIDTH, GRID_HEIGHT )grid.configure( INIT_CONFIG )# Play the game.draw( grid )for i in range( NUM_GENS ):evolve( grid )draw( grid )def evolve( grid ):liveCells = list()for i in range( grid.numRows() ):for j in range( grid.numCols() ):neighbors = grid.numLiveNeighbors( i, j )# 1. If a cell is alive and has either two or three live neighbors, the cell remains alive in the next generation. # The neighbors are the eight cells immediately surrounding a cell: vertically, horizontally, and diagonally.  # 2. A living cell that has no live neighbors or a single live neighbor dies from isolation in the next generation.# 3. A living cell that has four or more live neighbors dies from overpopulation in the next generation.# 4. A dead cell with exactly three live neighbors results in a birth and becomes alive in the next generation.# All other dead cells remain dead in the next generation.if (neighbors == 2 and grid.isLiveCell( i, j )) or \(neighbors == 3):liveCells.append( (i, j) )grid.configure( liveCells )def draw( grid ):printfor i in range( grid.numRows() ):for j in range( grid.numCols() ):if grid.isLiveCell( i, j):print '@',else:print '.',printmain()