遞歸
| 概念與特性 | 函數調?函數?身的編程?式叫做遞歸,調?為”遞“,返回為”歸“ |
| 三個條件 | 1. ?個問題的解可以分解為多個?問題的解; 2. 分解之后的?問題,除了數據規模不同,求解思路跟原問題相同; 3. 存在遞歸終?條件; |
| 編程技巧 | 1. 尋找將?問題分解為?問題求解的規律; 2. 找出遞推公式和終?條件,將其直接翻譯成代碼; 3. 切記不要???層?層的遞歸; 換句話說,也就是:如果?個問題A可以分解為若??問題B、C、D,我們可以假設?問題B、C、D已經解決,在此基礎上思考如何解決問題A。 我們只需要思考問題A與?問題B、C、D兩層之間的關系即可,不需要?層?層往下思考?問題與??問題,??問題與???問題之間的關系。 ? |
| 應?場景 | 遞歸是?種應??常?泛編程技巧,很多數據結構和算法的編碼實現都要 ?到遞歸,?如快排、歸并排序、DFS(深度優先搜索算法)、?叉樹遍歷、回溯等; |
| 其他知識點 | 1. 避免堆棧溢出(限制調?層次;遞歸改為迭代;尾遞歸優化); 2. 避免重復計算(利?備忘錄); |
| 掌握程度 | 1. 熟練編寫斐波那契數列、全排列、?皇后、快速排序;歸并排序、DFS、?叉樹遍歷、鏈表反轉遞歸實現等; |
排序
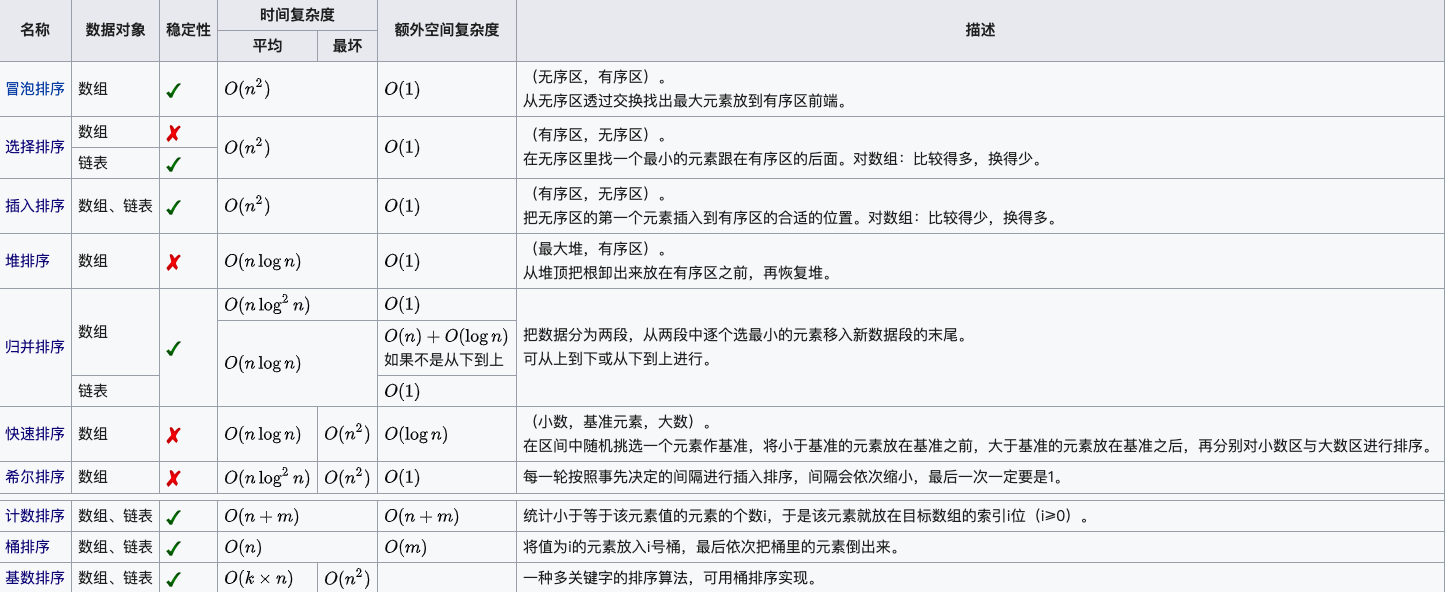
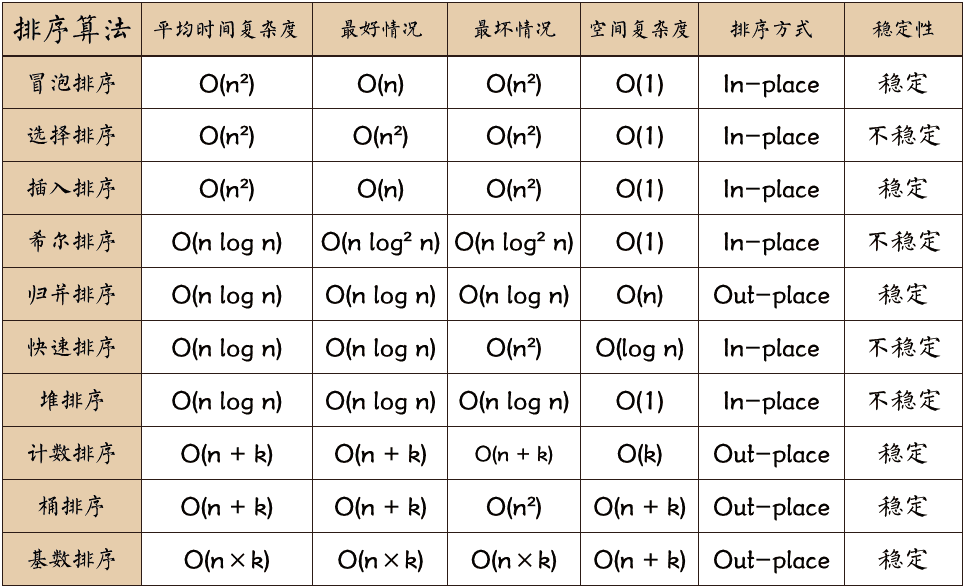
| 概念與特性 | 1. 穩定性:如果待排序的序列中存在值相等的元素,經過排序之后,相等元素之間原有的先后順序不變; 2. 原地:不額外申請?常量級的空間來臨時存儲排序數據;原地排序算法并不?定空間復雜度是O(1),空間復雜度是O(1)的排序算法?定是原地排序算法,?如快速排序是原地排序算法,但因為?到遞歸,函數調?棧會消耗?常量級的空間,所以,空間復雜度并?O(1),是O(logn)。 | |
| O(n^2) | 冒泡排序 | 冒泡排序是穩定原地排序算法。 整個冒泡排序過程包含多遍冒泡操作。每次冒泡操作都會遍歷整個數組,依次對相鄰的元素進??較,看是否滿???關系要求,如果不滿?,就將它們互換位置。?次冒泡操作會讓?少?個元素移動到它應該在的位置,重復n次,就完成了n個數據的 排序?作。 |
| 插?排序 | 插?排序是穩定原地排序算法。?先,我們將數組中的數據分為兩個區間,已排序區間和未排序區間。初始已排序區間只有?個元素,就是數組中的第?個元素。插?算法的核?思想是取未排序區間中的元素,在已排序區間中找到合適的插?位置將其插?,并保證已排序區間數據?直有序。重復這個過程,直到未排序區間中元素為空,算法結束。 | |
| 選擇排序 | 選擇排序算法是?穩定原地排序算法。其實現思路有點類似插?排序,也分已排序區間和未排序區間。 但不同點在于,選擇排序算法每次會從未排序區間中,找到最? 的元素,將其放到已排序區間的末尾。 | |
| O(nlogn) | 快速排序 | 快速排序是?穩定原地排序算法。空間復雜度是O(logn)。 如果要排序數組中下標從p到r之間的?組數據,我們選擇p到r之 間的任意?個數據作為pivot(分區點),然后,遍歷p到r之間 的數據,將?于pivot的放到左邊,將?于pivot的放到右邊,將 pivot放到中間。經過這?步驟之后,p到r之間的數據就被分成 了三個部分。假設pivot現在所在位置的下標是q,那p到q-1之 間數據都?于pivot,中間是pivot,q+1到r之間的數據都?于 pivot。根據分治、遞歸的處理思想,我們遞歸排序下標從p到 q-1之間的數據和下標從q+1到r之間的數據,直到區間縮?為 1,就說明所有的數據都有序了。 遞推公式:quickSort(p…r)=quickSort(p…q-1) & quickSort(q+1…r) |
| 歸并排序 | 歸并排序是穩定?原地排序算法。空間復雜度是O(n)。 如果要排序?個數組,我們先把數組從中間分成前后兩部分,然后,對前后兩部分分別排序,再將排好序的兩部分合并在?起,這樣整個數組就都有序了。遞推公式:mergeSort(p…r)=merge(mergeSort(p…q), mergeSort(q+1… r)) | |
| O(n) | 桶排序 | 桶排序,顧名思義,會?到“桶”,核?思想是將要排序的數據分到?個有序的桶?,每個桶?的數據再單獨進?排序。桶內排完序之后,再把每個桶?的數據按照順序依次取出,組成的序列就是有序的了。要排序的數據需要很容易就能劃分成m個桶,并且,桶與桶之間 有著天然的??順序。這樣每個桶內的數據都排完序之后,桶與桶之間的數據不需要再進?排序。 |
| 計數排序 | 實際上,計數排序是桶排序的?種特殊情況。當要排序的n個數據,所處的范圍并不?的時候,?如最?值是k,我們就可以把數據劃分成k個桶。每個桶內的數據值都是相同的,省掉了桶內排序的時間。 | |
| 基數排序 | 基數排序對要排序的數據也是有要求的,需要可以分割出獨?的“位”來?較,?且位之間有遞進的關系:如果a數據的?位? b數據?,那剩下的低位就不??了。除此之外,每?位的數 據范圍不能太?,可以使?其他線性排序算法來排序,否則,基數排序的時間復雜度就?法做到O(n)了。 | |
| 應?場景 | ?程中的排序函數?般使?O(nlogn)的快排、歸并或者堆排序作為主排序算 法,當數據規模較?時,轉?選擇使?更加簡單的插?排序。 | |
| 其他知識點 | 為了避免快速排序時間復雜度退化為極端情況O(n^2),我們使?更加?級的 分區點選擇?式,?如三數取中法、隨機法等。 | |
| 掌握程度 | 1. 熟練掌握冒泡、插?、選擇、快速、歸并排序的原理、代碼實現; 2. 熟練掌握快速、歸并排序的時間和空間復雜度分析; 3. 掌握桶排序、計數排序、基數排序的原理 | |
?分查找
| 概念與特性 | ?分查找針對的是?個有序的數據集合,查找思想有點類似分治思想。每次都通過跟區間的中間元素對?,將待查找的區間縮?為之前的?半,直到找到要查找的元素,或者區間被縮?為0。 |
| 操作與復雜度 | ?分查找的時間復雜度是O(logn) |
| ?分查找變體 | 變體?:查找第?個值等于給定值的元素 變體?:查找最后?個值等于給定值的元素 變體三:查找第?個?于等于給定值的元素 變體四:查找最后?個?于等于給定值的元素 |
| 掌握程度 | 熟練掌握?分查找、?分查找變體的代碼實現 |
相關圖片
?
參考鏈接
- 菜鳥教程



















