在一大堆數中求其前k大或前k小的問題，簡稱TOP-K問題。而目前解決TOP-K問題最有效的算法即是BFPRT算法，其又稱為中位數的中位數算法，該算法由Blum、Floyd、Pratt、Rivest、Tarjan提出，最壞時間復雜度為O(n)O(n)。

讀者要會快速排序相關知識，如果不會請看這里：

https://blog.csdn.net/hebtu666/article/details/81434236排序，大家在里面找快速排序閱讀即可。

?

我們以前寫過快排的改進求前k大或前k小，但是快排不可避免地存在退化問題，即使我們用了隨機數等優化，最差情況不可避免的退化到了O(N^2），而BFPRT就解決了這個問題，主要的思想精華就是怎么選取劃分值。

我們知道，經典快排是選第一個數進行劃分。而改進快排是隨機選取一個數進行劃分，從概率上避免了基本有序情況的退化。而BFPRT算法選劃分值的規則比較特殊，保證了遞歸最小的縮減規模也會比較大，而不是每次縮小一個數。

這個劃分值如何劃分就是重點。

如何讓選取的點無論如何都不會太差。

1、將n個元素劃分為n/5個組，每組5個元素
2、對每組排序，找到n/5個組中每一組的中位數；?
3、對于找到的所有中位數，調用BFPRT算法求出它們的中位數，作為劃分值。

下面說明為什么這樣找劃分值。

我們先把數每五個分為一組。

同一列為一組。

排序之后，第三行就是各組的中位數。

我們把第三行的數構成一個數列，遞歸找，找到中位數。

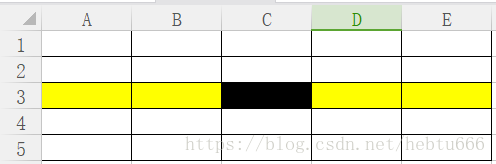
這個黑色框為什么找的很好。

因為他一定比A3、B3大，而A3、B3、C3又在自己的組內比兩個數要大。

我們看最差情況：求算其它的數都比c3大，我們也能在25個數中縮小九個數的規模。大約3/10.

我們就做到了最差情況固定遞減規模，而不是可能縮小的很少。

下面代碼實現：

public class BFPRT {
//前k小public static int[] getMinKNumsByBFPRT(int[] arr, int k) {if (k < 1 || k > arr.length) {return arr;}int minKth = getMinKthByBFPRT(arr, k);int[] res = new int[k];int index = 0;for (int i = 0; i != arr.length; i++) {if (arr[i] < minKth) {res[index++] = arr[i];}}for (; index != res.length; index++) {res[index] = minKth;}return res;}
//第k小public static int getMinKthByBFPRT(int[] arr, int K) {int[] copyArr = copyArray(arr);return select(copyArr, 0, copyArr.length - 1, K - 1);}public static int[] copyArray(int[] arr) {int[] res = new int[arr.length];for (int i = 0; i != res.length; i++) {res[i] = arr[i];}return res;}
//給定一個數組和范圍，求第i小的數public static int select(int[] arr, int begin, int end, int i) {if (begin == end) {return arr[begin];}int pivot = medianOfMedians(arr, begin, end);//劃分值int[] pivotRange = partition(arr, begin, end, pivot);if (i >= pivotRange[0] && i <= pivotRange[1]) {return arr[i];} else if (i < pivotRange[0]) {return select(arr, begin, pivotRange[0] - 1, i);} else {return select(arr, pivotRange[1] + 1, end, i);}}
//在begin end范圍內進行操作public static int medianOfMedians(int[] arr, int begin, int end) {int num = end - begin + 1;int offset = num % 5 == 0 ? 0 : 1;//最后一組的情況int[] mArr = new int[num / 5 + offset];//中位數組成的數組for (int i = 0; i < mArr.length; i++) {int beginI = begin + i * 5;int endI = beginI + 4;mArr[i] = getMedian(arr, beginI, Math.min(end, endI));}return select(mArr, 0, mArr.length - 1, mArr.length / 2);//只不過i等于長度一半，用來求中位數}
//經典partition過程public static int[] partition(int[] arr, int begin, int end, int pivotValue) {int small = begin - 1;int cur = begin;int big = end + 1;while (cur != big) {if (arr[cur] < pivotValue) {swap(arr, ++small, cur++);} else if (arr[cur] > pivotValue) {swap(arr, cur, --big);} else {cur++;}}int[] range = new int[2];range[0] = small + 1;range[1] = big - 1;return range;}
//五個數排序，返回中位數public static int getMedian(int[] arr, int begin, int end) {insertionSort(arr, begin, end);int sum = end + begin;int mid = (sum / 2) + (sum % 2);return arr[mid];}
//手寫排序public static void insertionSort(int[] arr, int begin, int end) {for (int i = begin + 1; i != end + 1; i++) {for (int j = i; j != begin; j--) {if (arr[j - 1] > arr[j]) {swap(arr, j - 1, j);} else {break;}}}}
//交換值public static void swap(int[] arr, int index1, int index2) {int tmp = arr[index1];arr[index1] = arr[index2];arr[index2] = tmp;}
//打印public static void printArray(int[] arr) {for (int i = 0; i != arr.length; i++) {System.out.print(arr[i] + " ");}System.out.println();}public static void main(String[] args) {int[] arr = { 6, 9, 1, 3, 1, 2, 2, 5, 6, 1, 3, 5, 9, 7, 2, 5, 6, 1, 9 };// sorted : { 1, 1, 1, 1, 2, 2, 2, 3, 3, 5, 5, 5, 6, 6, 6, 7, 9, 9, 9 }printArray(getMinKNumsByBFPRT(arr, 10));}
}

?