上次發操作系統筆記，很快瀏覽上萬，這次數據結構比上次硬核的多哦，同樣的會發超硬核代碼，關注吧。

超硬核！操作系統學霸筆記，考試復習面試全靠它

?

第一次筆記（復習c，課程概述）

第一節課復習了c語言的一些知識，并簡單介紹了數據結構這門課程。

1、引用和函數調用：

1.1引用：對一個數據建立一個“引用”，他的作用是為一個變量起一個別名。這是C++對C語言的一個重要補充。

用法很簡單：

int?a = 5;

int?&b = a;

b是a別名，b與a代表的是同一個變量，占內存中同一個存儲單元，具有同一地址。

注意事項：

聲明一個引用，同時必須初始化，及聲明它代表哪一個變量。（作為函數參數時不需要初始化）
?
在聲明一個引用后，不能再作為另一變量的引用。

? ? ?3。不能建立引用數組。

1.2函數調用：

其實還是通過函數來理解了一下引用

void Myswap1(int a,int b)
{int c = a;a = b;b = c;
}void Myswap2(int &a,int &b)
{int c = a;a = b;b = c;
}void Myswap3(int *pa,int *pb)
{int c = *pa;*pa = *pb;*pb = c;
}

這三個函數很簡單，第一個只傳了值進來，不改變全局變量；而第三個也很熟悉，就是傳遞了地址，方便操作。依舊是“值傳遞”的方式，只不過傳遞的是變量的地址而已；那二就徹底改變了這些東西，引用作為函數參數，傳入的實參就是變量，而不是數值，真正意義上的“變量傳遞”。

2、數組和指針：

這一塊講得比較簡單，就是基本知識。

主要內容：

1、函數傳數組就是傳了個指針，這個大家都知道，所以傳的時候你寫arr[],里面寫多少，或者不寫，都是沒關系的，那你后面一定要放一個變量來把數組長度傳進來。

2、還有就是，定義：int arr[5]，你訪問越界是不會報錯的，但是邏輯上肯定就沒有道理了。那用typedef int INTARR[3];訪問越界，在vs上會報錯，要注意。

3、再說一下指針和數組名字到底有什么區別？這本來就是兩個東西，可能大家沒注意罷了。

第一：指針可以自增，數組名不行，因為是常量啊。

第二：地址不同，雖然名字[n]，都可以這樣用，但是數組名地址就是第一個元素地址。指針地址就是那個指針的地址，指針里存的才是第一個元素地址。

第三：sizeof（），空間不一樣，數組是占數組那么大空間。指針是四個字節。

本來就是倆東西，這么多不同都是本質不同的體現。

3、結構體：

也是講的基本操作，基本就是這個東西：

typedef struct Date
{int Year;int Month;int Day;struct Date *pDate;
}Date, *pDate;

1、內部無指向自己的指針才可以第一行先不起名字。

2、內部不能定義自己的，如果能的話那空間不就無限了么。很簡單的邏輯

指針我不習慣，還是寫Date *比較順眼

3、有同學沒注意：訪問結構體里的東西怎么訪問？

Date.這種形式，或者有指向這個節點的指針p可以p->這種形式，別寫錯了。

4、還有就是結構體能直接這么賦值：

?? Date d1 = {2018,9,11};

我竟然不知道，以前還傻乎乎的一個一個賦值呢。

5、還有，想寫一下結構體有什么優點。。

這一塊可能寫的就不好了，因為不是老師講的。。

比如學生成績，如果不用結構體，我們一個學生可能有十幾個信息，那定義變量和操作就很煩瑣了，數據結構有一種松散的感覺。用一個結構體來表示更好，無論是程序的可讀性還是可移植性還是可維護性，都得到提升。還有就是函數調用的時候，傳入相當多的參數，又想操作或者返回，那是很麻煩的事。現在只傳入一個結構體就好了，操作極其簡單。總結一下就是好操作，中看中用，有機地組織了對象的屬性。以修改結構體成員變量的方法代替了函數(入口參數)的重新定義。

基本就這樣吧。

6、還有就是它了：typedef int INTARR[3];這樣直接定義了一個數據類型，長度為3的數組，然后直接這樣用就可以了：

INTARR arr1;

回憶完C語言儲備知識，然后講了數據結構的基本概念

數據結構是一門研究非數值計算的程序設計問題中計算機的操作對象以及他們之間的關系和操作等的學科。

數據：是對客觀事物的符號表示，在計算機中指能輸入到計算機中并被處理的符號總稱。

數據元素：數據的基本單位

數據項：數據的不可分割的最小單位

數據對象：性質相同的數據元素的集合。

舉例：動物是數據，某只動物是數據元素，貓狗是數據對象，顏色可以是數據項。

數據元素之間存在某種關系，這種關系成為結構。

四種基本結構：

集合：除了同屬一個集合無其他關系。

線性結構：一對一的關系

樹形結構：一對多的關系

圖狀結構：多對多的關系

第二次筆記（基本概念，時間空間復雜度）

今天繼續說明了一些基本概念，講解了時間空間復雜度。

（對于概念的掌握也很重要）

元素之間的關系在計算機中有兩種表示方法：順序映像和非順序映像，由此得到兩種不同的儲存結構：

順序存儲結構和鏈式存儲結構。

順序：根據元素在存儲器中的相對位置表示關系

鏈式：借助指針表示關系

數據類型：是一個值的集合和定義在這個值集上的一組操作的總稱。

抽象數據類型：是指一個數學模型以及定義在該模型上的一組操作。（僅僅取決于邏輯特性，與其在計算機內部如何表示和實現無關）

定義抽象數據類型的一種格式：

ADT name{

數據對象：<>

數據關系：<>

基本操作：<>

}ADT name

算法：是對特定問題求解步驟的一種描述。

算法五個特性：

有窮性：有窮的時間內完成，或者可以說是可接受的時間完成
確定性：對于相同的輸入只能得到相同的輸出
可行性：描述的操作都可以執行基本操作有限次來實現
輸入：零個或多個輸入。取自于某個特定對象的集合
輸出：一個或多個輸出

設計要求：正確性、可讀性、健壯性、效率與低存儲量需求。

執行頻度概念：是指通過統計算法的每一條指令的執行次數得到的。

執行頻度=算法中每一條語句執行次數的和

一般認定每條語句執行一次所需時間為單位時間（常數時間）O(1)

幾個小知識和小問題：

1）循環執行次數n+1次，不是n次。第一次執行i=1和判斷i<=n以后執行n次判斷和i++。所以該語句執行了n+1次。在他的控制下，循環體執行了n次。

2）四個并列程序段：分別為O(N),O(N^2),O(N^3),O(N*logN),整個程序時間復雜度為O(N^3)，因為隨著N的增長，其它項都會忽略

3）算法分析的目的是分析算法的效率以求改進

4）對算法分析的前提是算法必須正確

5）原地工作指的不是不需要空間，而是空間復雜度O(1)，可能會需要有限幾個變量。

實現統一功能兩種算法：時間O(2^N),O(N^10)，假設計算機可以運行10^7秒，每秒可執行基本操作10^5次，問可解問題規模各為多少？選哪個更為合適？

計算機一共可執行10^7*10^5=10^12次

第一種：n=log2,(10^12)=12log(2,10)

第二種：n=（10^12）^0.1

顯然1更適用。

雖然一般情況多項式算法比指數階更優

時間空間復雜度概述

找個時間寫一寫時間復雜度和一些問題分類，也普及一下這方面知識。

如何衡量一個算法好壞

很顯然，最重要的兩個指標：需要多久可以解決問題、解決問題耗費了多少資源

那我們首先說第一個問題，要多長時間來解決某個問題。那我們可以在電腦上真實的測試一下嘛，多種方法比一比，用時最少的就是最優的啦。

但是沒必要，我們可以通過分析計算來確定一個方法的好壞，用O()表示，括號內填入N、1，等式子。

這到底是什么意思呢？

簡單來說，就是這個方法，時間隨著數據規模變化而增加的快慢。時間可以當成Y，數據規模是X，y=f(x)，就這樣而已。但是f(x)不是準確的，只是一個大致關系，y=10x,我們也視作x，因為他的增長速度還是n級別的。現在就可以理解了：一般O(N)就是對每個對象訪問優先次數而已。請注意：O(1)它不是每個元素訪問一次，而是Y=1的感覺，y不隨x變化而變化，數據多大它的時間是不變的，有限的常數操作即可完成。

那我們就引入正規概念：

時間復雜度是同一問題可用不同算法解決，而一個算法的質量優劣將影響到算法乃至程序的效率。算法分析的目的在于選擇合適算法和改進算法。

計算機科學中，算法的時間復雜度是一個函數，它定性描述了該算法的運行時間。這是一個關于代表算法輸入值的字符串的長度的函數。時間復雜度常用大O符號表述，不包括這個函數的低階項和首項系數。使用這種方式時，時間復雜度可被稱為是漸近的，它考察當輸入值大小趨近無窮時的情況。

注意：文中提到：不包括這個函數的低階項和首項系數。什么意思呢？就是說10n,100n,哪怕1000000000n,還是算做O(N)，而低階項是什么意思？不知大家有沒有學高等數學1，里面有最高階無窮大，就是這個意思。舉個例子。比如y=n*n*n+n*n+n+1000

就算做o(n*n*n),因為增長速率最大，N*N及其它項增長速率慢，是低階無窮大，n無限大時，忽略不計。

那接著寫：o(n*n*n)的算法一定不如o(n)的算法嗎？也不一定，因為之前說了，時間復雜度忽略了系數，什么意思？o(n)可以是10000000n，當n很小的時候，前者明顯占優。

所以算法要視實際情況而定。

算法的時間復雜度常見的有：
常數階 O(1)，對數階 O(log n)，線性階 O(n)，
線性對數階 O(nlog n)，平方階 O(n^2)，立方階 O(n^3)，…，
k 次方階O(n^k)，指數階 O(2^n)，階乘階 O(n!)。

常見的算法的時間復雜度之間的關系為：
?????? O(1)<O(log n)<O(n)<O(nlog n)<O(n^2)<O(2^n)<O(n!)<O(n^n)?

我們在競賽當中，看見一道題，第一件事就應該是根據數據量估計時間復雜度。

計算機計算速度可以視作10^9,如果數據量是10000，你的算法是O(N*N)，那就很玄，10000*10000=10000 0000，別忘了還有常數項，這種算法只有操作比較簡單才可能通過。你可以想一想O(nlog n)的算法一般就比較穩了。那數據量1000，一般O(N*N)就差不多了，數據量更小就可以用復雜度更高的算法。大概就這樣估算。

當 n 很大時，指數階算法和多項式階算法在所需時間上非常
懸殊。因此，只要有人能將現有指數階算法中的任何一個算法化
簡為多項式階算法，那就取得了一個偉大的成就。

體會一下：

空間復雜度也是一樣，用來描述占空間的多少。

注意時間空間都不能炸。

所以才發明了那么多算法。

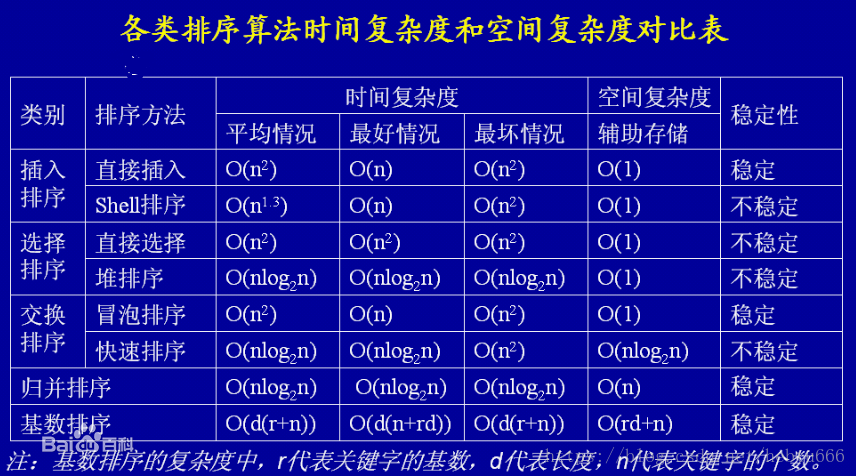
符上排序算法的時間空間表，體會一下：

排序博客：加深對時間空間復雜度理解

https://blog.csdn.net/hebtu666/article/details/81434236

?

引入：算法優化

想寫一系列文章，總結一些題目，看看解決問題、優化方法的過程到底是什么樣子的。

系列問題一：斐波那契數列問題

在數學上，斐波納契數列以如下被以遞歸的方法定義：F(0)=0，F(1)=1, F(n)=F(n-1)+F(n-2)（n>=2，n∈N*）根據定義，前十項為1, 1, 2, 3, 5, 8, 13, 21, 34, 55

問題一：

給定一個正整數n，求出斐波那契數列第n項（這時n較小）

解法一：最笨，效率最低，暴力遞歸，完全是抄定義。請看代碼

def f0(n):if n==1 or n==2:return 1return f(n-1)+f(n-2)

分析一下，為什么說遞歸效率很低呢？咱們來試著運行一下就知道了：

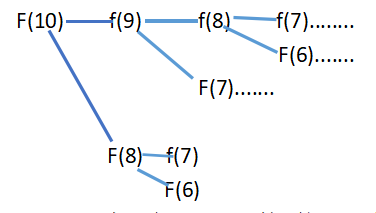
比如想求f(10)，計算機里怎么運行的？

每次要計算的函數量都是指數型增長，時間復雜度O(2^(N/2))<=T(N)<=O(2^N),效率很低。效率低的原因是，進行了大量重復計算，比如圖中的f(8),f(7).....等等，你會發現f(8)其實早就算過了，但是你后來又要算一遍。

如果我們把計算的結果全都保存下來，按照一定的順序推出n項，就可以提升效率，斐波那契（所有的一維）的順序已經很明顯了，就是依次往下求。。

優化1

def f1(n):if n==1 or n==2:return 1l=[0]*nl[0],l[1]=1,1for i in range(2,n):l[i]=l[i-1]+l[i-2]return l[-1]

時間復雜度o(n)，依次往下打表就行，空間o(n).

繼續優化：既然只求第n項，而斐波那契又嚴格依賴前兩項，那我們何必記錄那么多值呢？記錄前兩項就行了

優化2

def f2(n):a,b=1,1for i in range(n-1):a,b=b,a+breturn a

此次優化做到了時間o(n),空間o(1)

附：這道題掌握到這里就可以了，但是其實有時間o(log2n)的方法

優化三：

學習過線性代數的同學們能夠理解：

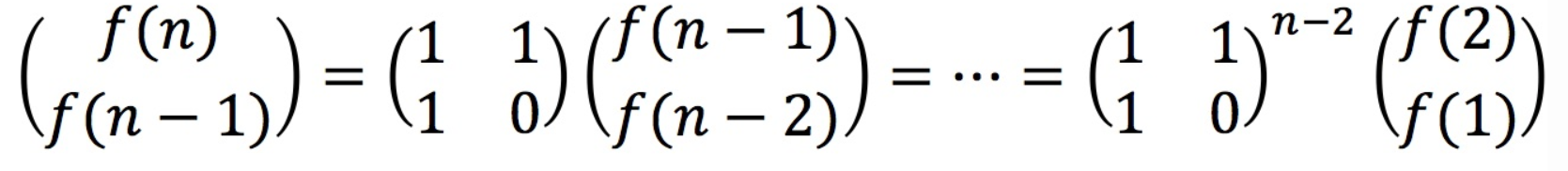
結合快速冪算法，我們可以在o(log2n)內求出某個對象的n次冪。(在其它專題詳細講解)

注意：只有遞歸式不變，才可以用矩陣+快速冪的方法。

注：優化三可能只有在面試上或競賽中用，當然，快速冪還是要掌握的。

經過這個最簡單的斐波那契，大家有沒有一點感覺了？

好，我們繼續往下走

(補充：pat、藍橋杯原題，讓求到一萬多位，結果模一個數。

可以每個結果都對這個數取模，否則爆內存，另：對于有多組輸入并且所求結果類似的題，可以先求出所有結果存起來，然后直接接受每一個元素，在表中查找相應答案)

問題二：

一只青蛙一次可以跳上1級臺階，也可以跳上2級。求該青蛙跳上一個n級的臺階總共有多少種跳法。

依舊是找遞推關系，分析：跳一階，就一種方法，跳兩階，它可以一次跳兩個，也可以一個一個跳，所以有兩種，三個及三個以上，假設為n階，青蛙可以是跳一階來到這里，或者跳兩階來到這里，只有這兩種方法。它跳一階來到這里，說明它上一次跳到n-1階，同理，它也可以從n-2跳過來，f（n）為跳到n的方法數，所以，f(n)=f(n-1)+f(n-2)

和上題的優化二類似。

因為遞推式沒變過，所以可以用優化三

問題三：

我們可以用2*1的小矩形橫著或者豎著去覆蓋更大的矩形。請問用n個2*1的小矩形無重疊地覆蓋一個2*n的大矩形，總共有多少種方法？提示，大矩形看做是長度吧

請讀者自己先思考一下吧。。。仔細看題。。仔細思考

如果n是1，只有一種，豎著放唄；n是2，兩種：

，

n等于3，三種：

題意應該理解了吧？

讀到這里，你們應該能很快想到，依舊是斐波那契式遞歸啊。

對于n>=3:怎么能覆蓋到三？只有兩種辦法，從n-1的地方豎著放了一塊，或者從n-2的位置橫著放了兩塊唄。

和問題二的代碼都不用變。

問題四：

給定一個由0-9組成的字符串，1可以轉化成A，2可以轉化成B。依此類推。。25可以轉化成Y，26可以轉化成z，給一個字符串，返回能轉化的字母串的有幾種？

比如：123，可以轉化成

1 2 3變成ABC，

12 3變成LC，

1 23變成AW，三種，返回三，

99999，就一種：iiiii，返回一。

分析：求i位置及之前字符能轉化多少種。

兩種轉化方法，一，字符i自己轉換成自己對應的字母，二，和前面那個數組成兩位數，然后轉換成對應的字母

假設遍歷到i位置，判斷i-1位置和i位置組成的兩位數是否大于26，大于就沒有第二種方法，f(i)=f(i-1),想反，等于f(i-1)+f(i-2)

注意：遞歸式不確定，不能用矩陣快速冪

(這幾個題放到這里就是為了鍛煉找遞歸關系的能力，不要只會那個爛大街的斐波那契)

'''
斐波那契問題：
斐波納契數列以如下被以遞歸的方法定義：
F(1)=1
F(2)=1
F(n)=F(n-1)+F(n-2)（n>=2，n∈N*）
'''
#暴力抄定義,過多重復計算
def f0(n):if n==1 or n==2:return 1return f(n-1)+f(n-2)
#記錄結果后依次遞推的優化，時間O(N)
def f1(n):if n==1 or n==2:return 1l=[0]*nl[0],l[1]=1,1for i in range(2,n):l[i]=l[i-1]+l[i-2]return l[-1]
#既然嚴格依賴前兩項，不必記錄每一個結果，優化空間到O(1)
def f2(n):a,b=1,1for i in range(n-1):a,b=b,a+breturn a

第三次筆記（線性表結構和順序表示）

?

這節課介紹了線性表結構和順序表示的一部分內容。

操作太多，而且書上有，就不一一介紹分析了。

線性表定義：n個數據元素的有限序列。

特點：

存在唯一一個稱作“第一個”的元素。
存在唯一一個稱作“最后一個”的元素
除最后一個元素外，集合中每一個元素都只有一個直接前趨
除最后一個元素外，集合中每一個元素都只有一個直接后繼

注意1、2條：證明循環的序列不是線性表

注意：

1)線性表從1開始,線性表第一個元素對應到數組中下標是0.

2)函數通過引用對線性表的元素進行修改即可

3)數組比較特別，它即可視為邏輯結構，又可視為存儲結構。

4)每一個表元素都是不可再分的原子數據。一維數組可以視為線性表，二維數組不可以，在邏輯上它最多可以有兩個直接前趨和直接后繼。

5)線性表具有邏輯上的順序性，在序列中各元素有其先后次序，各個數據元素在線性表中的邏輯位置只取決于序號。

順序表：是線性表的循序儲存結構，以物理位置表示邏輯關系，任意元素可以隨機存取。用一組地址連續的存儲單元依次存儲線性表中的元素。邏輯順序和物理順序是一致的。可以順序訪問，也可隨機訪問。

順序表存儲：

這些定式還是很重要的，比如define typedef等，真正實現時最好就這樣寫，不要自己規定個長度和數據類型，這樣以后好維護、修改。

靜態存儲分配：

#define maxSize 100//顯式定義表長

Typedef int DataType;//定義數據類型

Typedef struct{

DataType data[maxSize];//靜態分配存儲表元素向量

Int n;//實際表中個數

}SeqList;

動態存儲分配：

#define maxSize 100//長度初始定義

Typedef int DataType;//定義數據類型

Typedef struct{

DataType *data;//動態分配數組指針

Int maxSize,n;//最大容量和當前個數

}SeqList;

初始動態分配：

Data=(DataType *)malloc(sizeof(DataType)* initSize);

C++:data=new DataType[initSize];

maxSize=initSize;n=0;

動態分配存儲，向量的存儲空間是在程序執行過程中通過動態存儲分配來獲取的。空間滿了就另外分配一塊新的更大的空間，用來代替原來的存儲空間，從而達到擴充的目的。

插入：需要查找，移動元素，概率上1，2，3....n，平均O(N)

刪除：同樣需要移動元素。填充被空出來的存儲單元。

在等概率下平均移動次數分別為n/2,(n-1)/2

?插入注意事項：

需要判斷是否已滿
要從后向前移動，否則會沖掉元素

刪除注意事項：

需要先判斷是否已空
需要把后方元素前移，要從前向后。

注意：線性表的順序存儲借用了一維數組，但是二者不同：

一維數組各非空結點可以不相繼存放，但順序表是相繼存放的
順序表長度是可變的，一維數組長度是確定的，一旦分配就不可變
一維數組只能按下標存取元素，順序表可以有線性表的所有操作。

第四次筆記（鏈表概述）

介紹了鏈表和基本操作

用一組物理位置任意的存儲單元來存放線性表的數據元素。這組存儲單元既可以是連續的，也可以是不連續的，甚至是零散分布在內存中的任意位置上的。因此，鏈表中元素的邏輯次序和物理次序不一定相同。

定義：

typedef  struct  Lnode{  //聲明結點的類型和指向結點的指針類型  ElemType         data;    //數據元素的類型 struct   Lnode  *next;   //指示結點地址的指針  
}Lnode, *LinkList;

struct Student
{ char num[8];   //數據域char name[8];  //數據域int score;          //數據域struct Student *next;  // next 既是 struct Student // 類型中的一個成員，又指 // 向 struct Student 類型的數據。 
}Stu_1, Stu_2, Stu_3, *LL;

頭結點：在單鏈表的第一個結點之前人為地附設的一個結點。

帶頭結點操作會方便很多。

帶和不帶的我都寫過了

下面列出我見過的一些好題

1、

線性表的每個結點只能是一個簡單類型，而鏈表的每個結點可以是一個復雜類型。

```
正確
```
```
錯誤
```

錯，線性表是邏輯結構概念，可以順序存儲或鏈式儲，與元素數據類型無關。鏈表就是線性表的一種 ?前后矛盾

2、

若某線性表中最常用的操作是在最后一個元素之后插入一個元素和刪除第一個元素，則采用( ???)存儲方式最節省運算時間。

```
單鏈表
```
```
僅有頭指針的單循環鏈表
```
```
雙鏈表
```
```
僅有尾指針的單循環鏈表
```
對于A,B，C要想在尾端插入結點，需要遍歷整個鏈表。

對于D，要插入結點，只要改變一下指針即可，要刪除頭結點，只要刪除指針.next的元素即可。

3、注意：線性表是具有n個數據元素的有限序列，而不是數據項

4、

以下關于單向鏈表說法正確的是

如果兩個單向鏈表相交，那他們的尾結點一定相同

快慢指針是判斷一個單向鏈表有沒有環的一種方法

有環的單向鏈表跟無環的單向鏈表不可能相交

如果兩個單向鏈表相交，那這兩個鏈表都一定不存在環

自己多畫畫想想就明白了，關于快慢指針我以后會寫總結。

5、

鏈接線性表是順序存取的線性表?。?(?)

```
正確
```
```
錯誤
```

鏈接線性表可以理解為鏈表
線性表分為順序表和鏈表
順序表是順序存儲結構、隨機存取結構
鏈表是隨機存儲結構、順序存取結構

6、

typedef struct node_s{int item;struct node_s* next;
}node_t;
node_t* reverse_list(node_t* head)
{node_t* n=head;head=NULL;while(n){_________               }return head;}

空白處填入以下哪項能實現該函數的功能？

node_t* m=head; head=n; head->next=m; n=n->next;

node_t* m=n; n=n->next; m->next=head; head=m;

node_t* m=n->next; n->next=head; n=m; head=n;

```
head=n->next; head->next=n; n=n->next;
```

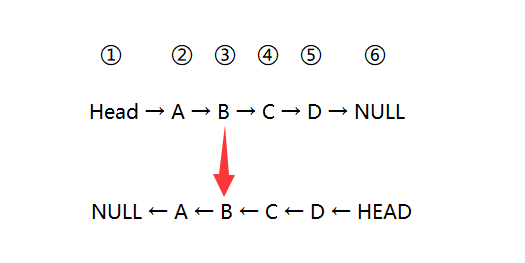
代碼的功能是要實現鏈表的反轉。為了方便闡述，每個結點用①②③④⑤⑥等來標示。

在執行while（n）循環之前，有兩句代碼：

node_t* n=head;

head=NULL;

這兩行代碼的中：第一句的作用是用一個臨時變量n來保存結點①，第二句是把head修改為NULL。

然后就開始遍歷了，我們看到while循環里的那四句代碼：

node_t* m=n; 
n=n->next; 
m->next=head; 
head=m；

先看前兩句，用m來保存n，然后讓n指向n的下一個結點，之所以復制 n 給 m ，是因為 n 的作用其實是? 控制while循環次數? 的作用，每循環一次它就要被修改為指向下一個結點。

再看后兩句，變量head在這里像是一個臨時變量，后兩句讓 m 指向了 head，然后 head 等于 m。

7、

若某表最常用的操作是在最后一個結點之后插入一個節點或刪除最后一二個結點，則采用（）省運算時間。

```
單鏈表
```
```
雙鏈表
```
```
單循環鏈表
```
```
帶頭結點的雙循環鏈表
```

帶頭結點的雙向循環鏈表，頭結點的前驅即可找到最后一個結點，可以快速插入，再向前可以找到最后一二個結點快速刪除

單鏈表找到鏈表尾部需要掃描整個鏈表

雙鏈表找到鏈表尾部也需要掃描整個鏈表

單循環鏈表只有單向指針，找到鏈表尾部也需要掃描整個鏈表

8、

單鏈表的存儲密度（ ?）

```
大于1
```
```
等于1
```
```
小于1
```
```
不能確定
```

全麥白

存儲密度 = 數據項所占空間 / 結點所占空間

9、完成在雙循環鏈表結點p之后插入s的操作是

s->prior=p; s->next=p->next; p->next->prior=s ; p->next=s;

10、用不帶頭結點的單鏈表存儲隊列,其隊頭指針指向隊頭結點,隊尾指針指向隊尾結點,則在進行出隊操作時()

```
僅修改隊頭指針
```
```
僅修改隊尾指針
```
```
隊頭、隊尾指針都可能要修改
```
```
隊頭、隊尾指針都要修改
```

當只有一個元素，出隊列時，要將隊頭和隊尾，指向-1.所以說隊頭和隊尾都需要修改

鏈表刷了幾百道吧，好題還有很多，以后接著更新

第六次筆記（鏈表選講/靜態鏈表）

本節課介紹了單鏈表的操作實現細節，介紹了靜態鏈表。

鏈表帶頭的作用：對鏈表進行操作時，可以對空表、非空表的情況以及對首元結點進行統一處理，編程更方便。

下面給出帶頭的單鏈表實現思路：

按下標查找：

判斷非法輸入，當 1 <?=i <=?n 時，i 的值是合法的。

p = L ->?next; j = 1;

while ( p && j < i ) { ?p = p ?->next; ++j; }

return?

按值查找：

?p = L1 ->?next;

?while ( p && p ->data!=key) ? ? ? ? ?p = p ->?next;

return;

插入：

判斷

查找

創建

插入

刪除：

查找

刪除

釋放內存

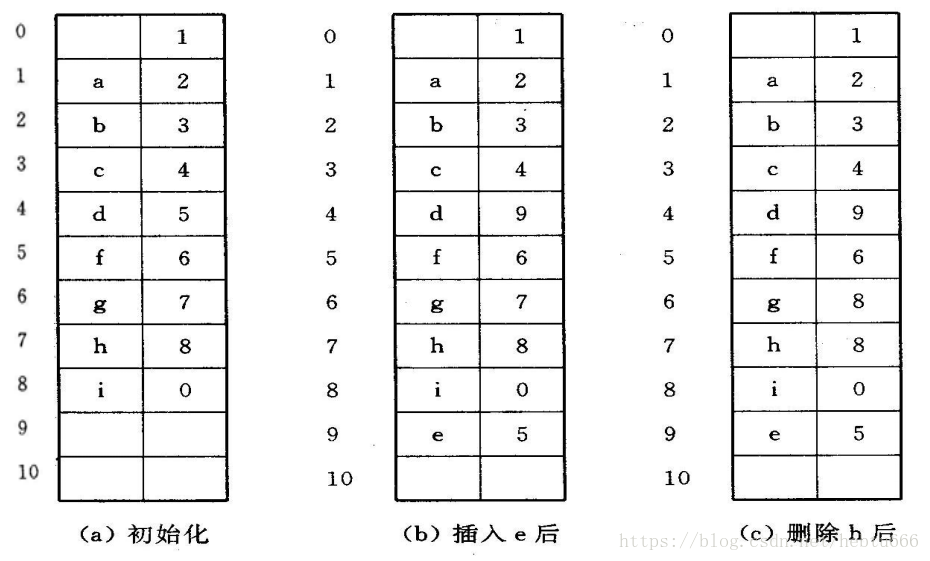
靜態鏈表

對于線性鏈表，也可用一維數組來進行描述。這種描述方法便于在沒有指針類型的高級程序設計語言中使用鏈表結構。

這種存儲結構，仍需要預先分配一個較大的空間，但在作為線性表的插入和刪除操作時不需移動元素，僅需修改指針，故仍具有鏈式存儲結構的主要優點。

表示：

#define MAXSIZE 1000 ? ? ?/ /鏈表的最大長度

typedef ?struct{ ? ? ?

? ? ElemType data； ? ? ? ?

? ? int cur；

}component, ?SLinkList[MAXSIZE]；

過程：

順序存儲線性表實現

在計算機中用一組地址連續的存儲單元依次存儲線性表的各個數據元素,稱作線性表的順序存儲結構。

順序存儲結構的主要優點是節省存儲空間，因為分配給數據的存儲單元全用存放結點的數據（不考慮c/c++語言中數組需指定大小的情況），結點之間的邏輯關系沒有占用額外的存儲空間。采用這種方法時，可實現對結點的隨機存取，即每一個結點對應一個序號，由該序號可以直接計算出來結點的存儲地址。但順序存儲方法的主要缺點是不便于修改，對結點的插入、刪除運算時，可能要移動一系列的結點。

優點：隨機存取表中元素。缺點：插入和刪除操作需要移動元素。

線性表中數據元素之間的關系是一對一的關系，即除了第一個和最后一個數據元素之外，其它數據元素都是首尾相接的（注意，這句話只適用大部分線性表，而不是全部。比如，循環鏈表邏輯層次上也是一種線性表（存儲層次上屬于鏈式存儲），但是把最后一個數據元素的尾指針指向了首位結點）。

給出兩種基本實現：

/*
靜態順序存儲線性表的基本實現
*/#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define LIST_INITSIZE 100
#define ElemType int
#define Status int
#define OK     1
#define ERROR  0typedef struct
{ElemType elem[LIST_INITSIZE];int length;
}SqList;//函數介紹
Status InitList(SqList *L); //初始化
Status ListInsert(SqList *L, int i,ElemType e);//插入
Status ListDelete(SqList *L,int i,ElemType *e);//刪除
void ListPrint(SqList L);//輸出打印
void DisCreat(SqList A,SqList *B,SqList *C);//拆分(按正負)，也可以根據需求改
//雖然思想略簡單，但是要寫的沒有錯誤，還是需要鍛煉coding能力的Status InitList(SqList *L)
{L->length = 0;//長度為0return OK;
}Status ListInsert(SqList *L, int i,ElemType e)
{int j;if(i<1 || i>L->length+1)return ERROR;//判斷非法輸入if(L->length == LIST_INITSIZE)//判滿{printf("表已滿");//提示return ERROR;//返回失敗}for(j = L->length;j > i-1;j--)//從后往前覆蓋，注意i是從1開始L->elem[j] = L->elem[j-1];L->elem[i-1] = e;//在留出的位置賦值(L->length)++;//表長加1return OK;//反回成功
}Status ListDelete(SqList *L,int i,ElemType *e)
{int j;if(i<1 || i>L->length)//非法輸入/表空return ERROR;*e = L->elem[i-1];//為了返回值for(j = i-1;j <= L->length;j++)//從前往后覆蓋L->elem[j] = L->elem[j+1];(L->length)--;//長度減1return OK;//返回刪除值
}void ListPrint(SqList L)
{int i;for(i = 0;i < L.length;i++)printf("%d ",L.elem[i]);printf("\n");//為了美觀
}void DisCreat(SqList A,SqList *B,SqList *C)
{int i;for(i = 0;i < A.length;i++)//依次遍歷A中元素{if(A.elem[i]<0)//判斷ListInsert(B,B->length+1,A.elem[i]);//直接調用插入函數實現尾插elseListInsert(C,C->length+1,A.elem[i]);}
}int main(void)
{//復制的SqList L;SqList B, C;int i;ElemType e;ElemType data[9] = {11,-22,33,-3,-88,21,77,0,-9};InitList(&L);InitList(&B);InitList(&C);for (i = 1; i <= 9; i++)ListInsert(&L,i,data[i-1]);printf("插入完成后L = : ");ListPrint(L);ListDelete(&L,1,&e);printf("刪除第1個后L = : ");ListPrint(L);DisCreat(L , &B, &C);printf("拆分L后B = : ");ListPrint(B);printf("拆分L后C = : ");ListPrint(C);printf("拆分L后L = : ");ListPrint(L);
}

靜態：長度固定

動態：不夠存放可以加空間（搬家）

/*
子任務名任務:1_2 動態順序存儲線性表的基本實現
*/#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
#define Status int
#define OVERFLOW -1
#define OK 1
#define ERROR 0
#define ElemType inttypedef struct
{ElemType * elem;int length;int listsize;
}SqList;
//函數介紹
Status InitList(SqList *L); //初始化
Status ListInsert(SqList *L, int i,ElemType e);//插入
Status ListDelete(SqList *L,int i,ElemType *e);//刪除
void ListPrint(SqList L);//輸出打印
void DeleteMin(SqList *L);//刪除最小Status InitList(SqList *L)
{L->elem = (ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType));//申請100空間if(!L->elem)//申請失敗return ERROR;L->length = 0;//長度0L->listsize = LIST_INIT_SIZE;//容量100return OK;//申請成功
}Status ListInsert(SqList *L,int i,ElemType e)
{int j;ElemType *newbase;if(i<1 || i>L->length+1)return ERROR;//非法輸入if(L->length >= L->listsize)//存滿了，需要更大空間{newbase = (ElemType*)realloc(L->elem,(L->listsize+LISTINCREMENT)*sizeof(ElemType));//大10的空間if(!newbase)//申請失敗return ERROR;L->elem = newbase;//調指針L->listsize+= LISTINCREMENT;//新容量}for(j=L->length;j>i-1;j--)//從后往前覆蓋L->elem[j] = L->elem[j-1];L->elem[i-1] = e;//在留出的位置賦值L->length++;//長度+1return OK;
}Status ListDelete(SqList *L,int i,ElemType *e)
{int j;if(i<1 || i>L->length)//非法輸入/表空return ERROR;*e = L->elem[i-1];//為了返回值for(j = i-1;j <= L->length;j++)//從前往后覆蓋L->elem[j] = L->elem[j+1];(L->length)--;//長度減1return OK;//返回刪除值
}void ListPrint(SqList L)
{int i;for(i=0;i<L.length;i++)printf("%d ",L.elem[i]);printf("\n");//為了美觀
}void DeleteMin(SqList *L)
{//表空在Listdelete函數里判斷int i;int j=0;//最小值下標ElemType *e;for(i=0;i<L->length;i++)//尋找最小{if(L->elem[i] < L->elem[j])j=i;}ListDelete(L,j+1,&e);//調用刪除，注意j要+1
}int main(void)
{SqList L;int i;ElemType e;ElemType data[9] = {11,-22,-33,3,-88,21,77,0,-9};InitList(&L);for (i = 1; i <= 9; i++){ListInsert(&L,i,data[i-1]);}printf("插入完成后 L = : ");ListPrint(L);ListDelete(&L, 2, &e);printf("刪除第 2 個后L = : ");ListPrint(L);DeleteMin(&L);printf("刪除L中最小值后L = : ");ListPrint(L);DeleteMin(&L);printf("刪除L中最小值后L = : ");ListPrint(L);DeleteMin(&L);printf("刪除L中最小值后L = : ");ListPrint(L);
}

單鏈表，不帶頭實現

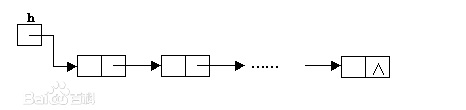
鏈表是一種物理存儲單元上非連續、非順序的存儲結構，數據元素的邏輯順序是通過鏈表中的指針鏈接次序實現的。鏈表由一系列結點（鏈表中每一個元素稱為結點）組成，結點可以在運行時動態生成。每個結點包括兩個部分：一個是存儲數據元素的數據域，另一個是存儲下一個結點地址的指針域。相比于線性表順序結構，操作復雜。由于不必須按順序存儲，鏈表在插入的時候可以達到O(1)的復雜度，比另一種線性表順序表快得多，但是查找一個節點或者訪問特定編號的節點則需要O(n)的時間，而線性表和順序表相應的時間復雜度分別是O(logn)和O(1)。

使用鏈表結構可以克服數組鏈表需要預先知道數據大小的缺點，鏈表結構可以充分利用計算機內存空間，實現靈活的內存動態管理。但是鏈表失去了數組隨機讀取的優點，同時鏈表由于增加了結點的指針域，空間開銷比較大。鏈表最明顯的好處就是，常規數組排列關聯項目的方式可能不同于這些數據項目在記憶體或磁盤上順序，數據的存取往往要在不同的排列順序中轉換。鏈表允許插入和移除表上任意位置上的節點，但是不允許隨機存取。鏈表有很多種不同的類型：單向鏈表，雙向鏈表以及循環鏈表。

下面給出不帶頭的單鏈表標準實現：

定義節點：

typedef struct node 
{ int data;struct node * next;
}Node;

尾插：

void pushBackList(Node ** list, int data) 
{ Node * head = *list;Node * newNode = (Node *)malloc(sizeof(Node));//申請空間newNode->data = data; newNode->next = NULL;if(*list == NULL)//為空*list = newNode;else//非空{while(head ->next != NULL)head = head->next;head->next = newNode;}
}

插入：

int insertList(Node ** list, int index, int data) 
{int n;int size = sizeList(*list); Node * head = *list; Node * newNode, * temp;if(index<0 || index>size) return 0;//非法newNode = (Node *)malloc(sizeof(Node)); //創建新節點newNode->data = data; newNode->next = NULL;if(index == 0) //頭插{newNode->next = head; *list = newNode; return 1; }for(n=1; n<index; n++) //非頭插head = head->next;if(index != size) newNode->next = head->next; //鏈表尾部next不需指定head->next = newNode; return 1;
}

按值刪除：

void deleteList(Node ** list, int data) 
{ Node * head = *list; Node * temp; while(head->next!=NULL) { if(head->next->data != data) { head=head->next; continue; } temp = head->next;if(head->next->next == NULL) //尾節點刪除head->next = NULL; else head->next = temp->next; free(temp);}    head = *list; if(head->data == data) //頭結點刪除{ temp = head; *list = head->next; head = head->next; free(temp); }
}

打印：

void printList(Node * head) 
{ Node * temp = head; for(; temp != NULL; temp=temp->next) printf("%d ", temp->data); printf("\n"); 
}

清空：

void freeList(Node ** list) 
{ Node * head = *list; Node * temp = NULL; while(head != NULL) //依次釋放{ temp = head; head = head->next; free(temp); } *list = NULL; //置空
}

別的也沒啥了，都是基本操作

有些代碼要分情況，很麻煩，可讀性較強吧

看我壓縮代碼：https://blog.csdn.net/hebtu666/article/details/81261043

雙鏈表帶頭實現

以前寫的不帶頭的單鏈表實現，當時也啥也沒學，好多東西不知道，加上一心想壓縮代碼，減少情況，所以寫得不太好。

請教了老師，首先是命名問題和代碼緊湊性等的改進。還有可讀性方面的改進，多寫了一些注釋。并且因為帶頭的比較好寫，好操作，所以標準寫法也不是很長，繁瑣。

下面貼代碼

#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef struct node{int key;//數據struct node * prev;//前驅struct node * next;//后繼
}Node;

初始化（帶頭）?

Node * list;
//初始化，這里·我們list不再是NULL，而是指向了一個節點
//這個改進方便了很多操作，也不用借助二重指針把list和next統一表示了void init(Node * list)//初始化
{list = (Node *)malloc(sizeof(Node));list->next = NULL;list->prev = NULL;
}

查找（不用再判斷一下空不空）

Node * find(int key,Node * list)
{Node * head = list->next;//從頭節點后面開始找while(head != NULL && head->key != key)//找到或空跳出head = head->next;return head;
}

打印

void printList(Node * list)//打印
{Node * temp = list->next;頭節點下一個開始while(temp != NULL){printf("%d ",temp->key);temp = temp->next;}printf("\n");
}

刪除指定結點

void delete(Node * list)//刪除指定結點
{list->prev->next = list->next;前面后面指針改了，再free自己即可list->next->prev = list->prev;free(list);
}

配合一下刪除：

void deleteKey(int key,Node * list)
{delete(find(key,list));
}

頭插：

void insertHead(int key,Node * list)//頭插
{Node * newNode = (Node *)malloc(sizeof(Node));//初始化newNode->key = key;newNode->next = list->next;//賦值后繼if(list->next != NULL)//如果有后繼，賦值后繼的前指針為新結點list->next->prev = newNode;list->next = newNode;//改頭newNode->prev = list;//賦值新結點前指針
}

按下標插入

單鏈表都寫了，我就不寫長度函數和判斷非法了，用的時候注意吧。

void insert(int key,Node * list,int index)
{Node * head=list;//最后指到要插位置的前一個即可Node * newNode = (Node *)malloc(sizeof(Node));//初始化newNode->key = key;while(index--)head = head->next;newNode->next = head->next;//修改指針newNode->prev = head;head->next = newNode;
}

指定某值后插入不寫了，和這個修改指針邏輯一樣，再傳一個find配合一下就行了。

然后簡單測試

int main()
{Node * list = NULL;init(list);insertHead(1,list);insertHead(2,list);insertHead(3,list);printList(list);deleteKey(2,list);printList(list);insert(10,list,0);printList(list);
}

第七次筆記（棧/隊列）

介紹棧和隊列基本概念和用法。

設輸入序列1、2、3、4，則下述序列中（）不可能是出棧序列。【中科院中國科技大學2005】

A. 1、2、3、4 ? ? ? ? ? ? ? ? ? ? ?B. 4、 3、2、1

C. 1、3、4、2 ? ? ? ? ? ? ? ? ? ? ?D.４、1、2、3

選D

我是一個個模擬來做的。

描述棧的基本型性質：

1、集合性：棧是由若干個元素集合而成，沒有元素（空集）成為空棧。

2、線性：除棧頂和棧底之外，任意元素均有唯一前趨和后繼。

3、運算受限：只在一端插入刪除的線性表即為棧

順序存儲和順序存取：順序存取是只能逐個存或取結構中的元素，例如棧。順序存儲是利用一個連續的空間相繼存放，例如棧可基于一維數組存放元素。

一個較早入棧的元素能否在后面元素之前出棧？如果后面元素壓在它上面，就不可以了。如果后面元素未壓入，它可以彈出。在其他元素前面。

棧與遞歸：

? 當在一個函數的運行期間調用另一個函數時，在運行該被調用函數之前，需先完成三件事： ?將實參等傳遞給被調用函數，保存返回地址（入棧）； ?為被調用函數的局部變量分配存儲區； ? ?將控制轉移到被調用函數的入口。 ?

從被調用函數返回調用函數之前，應該完成： ?保存被調函數的計算結果； ?釋放被調函數的數據區； ?按被調函數保存的返回地址（出棧）將控制轉移到調 ? ? ? ?用函數。

多個函數嵌套調用的規則是：后調用先返回。

?此時的內存管理實行“棧式管理”

隊列：

? ? ? ? 在多用戶計算機系統中，各個用戶需要使用 CPU 運行自己的程序，它們分別向操作系統提出使用 CPU 的請求，操作系統按照每個請求在時間上的先后順序，將其排成一個隊列，每次把CPU分配給隊頭用戶使用，當相應的程序運行結束，則令其出隊，再把CPU分配給新的隊頭用戶，直到所有用戶任務處理完畢。

以主機和打印機為例來說明，主機輸出數據給打印機打印，主機輸出數據的速度比打印機打印的速度要快得多，若直接把輸出的數據送給打印機打印，由于速度不匹配，顯然不行。解決的方法是設置一個打印數據緩沖區，主機把要打印的數據依此寫到這個緩沖區中，寫滿后就暫停輸出，繼而去做其它的事情，打印機就從緩沖區中按照先進先出的原則依次取出數據并打印，打印完后再向主機發出請求，主機接到請求后再向緩沖區寫入打印數據，這樣利用隊列既保證了打印數據的正確，又使主機提高了效率。

雙端隊列：

某隊列允許在其兩端進行入隊操作，但僅允許在一端進行出隊操作，若元素a,b,c,d,e依次入隊列后，再進行出隊操作，則不可能得到的順序是（）。?

A. bacde ? ? ? ? ? ? ? ?B. dbace ? ? ? ? ? ? ?C. dbcae ? ? ? ? ? ? ? ?D. ecbad

解析：出隊只能一端，所以abcde一定是這個順序。

反模擬入隊，每次只能在兩邊出元素。

棧/隊列互相模擬實現

用兩個棧來實現一個隊列，完成隊列的Push和Pop操作。隊列中的元素為int類型。

思路：大概這么想：用一個輔助棧把進第一個棧的元素倒一下就好了。

比如進棧1，2，3，4，5

第一個棧：

然后倒到第二個棧里

再倒出來，順序為1，2，3，4，5

實現隊列

然后要注意的事情：

1）棧2非空不能往里面倒數，順序就錯了。棧2沒數再從棧1倒。

2）棧1要倒就一次倒完，不倒完的話，進新數也會循序不對。

import java.util.Stack;public class Solution {Stack<Integer> stack1 = new Stack<Integer>();Stack<Integer> stack2 = new Stack<Integer>();public void push(int node) {stack1.push(node);}public int pop() {if(stack1.empty()&&stack2.empty()){throw new RuntimeException("Queue is empty!");}if(stack2.empty()){while(!stack1.empty()){stack2.push(stack1.pop());}}return stack2.pop();}
}

用兩個隊列實現棧，要求同上：

這其實意義不是很大，有些數據結構書上甚至說兩個隊列不能實現棧。

其實是可以的，只是時間復雜度較高，一個彈出操作時間為O(N)。

思路：兩個隊列，編號為1和2.

進棧操作：進1號隊列

出棧操作：把1號隊列全弄到2號隊列里，剩最后一個別壓入，而是返回。

最后還得把1和2號換一下，因為現在是2號有數，1號空。

僅僅有思考價值，不實用。

比如壓入1，2，3

隊列1：1，2，3

隊列2：空

依次彈出1，2，3：

隊列1里的23進入2號，3彈出

隊列1：空

隊列2：2，3

隊列2中3壓入1號，2彈出

隊列1：3

隊列2：空

隊列1中只有一個元素，彈出。

上代碼：

public class TwoQueueImplStack {Queue<Integer> queue1 = new ArrayDeque<Integer>();Queue<Integer> queue2 = new ArrayDeque<Integer>();
//壓入public void push(Integer element){//都為空，優先1if(queue1.isEmpty() && queue2.isEmpty()){queue1.add(element);return;}//1為空，2有數據，放入2if(queue1.isEmpty()){queue2.add(element);return;}//2為空，1有數據，放入1if(queue2.isEmpty()){queue1.add(element);return;}}
//彈出public Integer pop(){//兩個都空，異常if(queue1.isEmpty() && queue2.isEmpty()){try{throw new Exception("satck is empty!");}catch(Exception e){e.printStackTrace();}}	//1空，2有數據，將2中的數據依次放入1，最后一個元素彈出if(queue1.isEmpty()){while(queue2.size() > 1){queue1.add(queue2.poll());}return queue2.poll();}//2空，1有數據，將1中的數據依次放入2，最后一個元素彈出if(queue2.isEmpty()){while(queue1.size() > 1){queue2.add(queue1.poll());}return queue1.poll();}return (Integer)null;}
//測試public static void main(String[] args) {TwoQueueImplStack qs = new TwoQueueImplStack();qs.push(2);qs.push(4);qs.push(7);qs.push(5);System.out.println(qs.pop());System.out.println(qs.pop());qs.push(1);System.out.println(qs.pop());}
}

第八次筆記?（串）

串的概念：串（字符串）：是由 0 個或多個字符組成的有限序列。通常記為：s =‘ a1 a2 a3 … ai …an ?’ ( n≥0 )。

串的邏輯結構和線性表極為相似。

一些串的類型：

空串：不含任何字符的串，長度 = 0。

空格串：僅由一個或多個空格組成的串。

子串：由串中任意個連續的字符組成的子序列。

主串：包含子串的串。

位置：字符在序列中的序號。

子串在主串中的位置：子串的首字符在主串中的位置。

空串是任意串的子串，任意串是其自身的子串。

串相等的條件：當兩個串的長度相等且各個對應位置的字符都相等時才相等。

實現：

因為串是特殊的線性表，故其存儲結構與線性表的存儲結構類似，只不過組成串的結點是單個字符。

定長順序存儲表示

也稱為靜態存儲分配的順序串。即用一組地址連續的存儲單元依次存放串中的字符序列。

串長：可能首字符記錄（顯式）或\0結尾（隱式）

定長順序存儲表示時串操作的缺點：串的某些操作受限（截尾），如串的聯接、插入、置換

堆分配存儲表示 ?

存儲空間在程序執行過程中動態分配，malloc() 分配一塊實際串長所需要的存儲空間（“堆”）

堆存儲結構的優點：堆存儲結構既有順序存儲結構的特點，處理（隨機取子串）方便，操作中對串長又沒有任何限制，更顯靈活，因此在串處理的應用程序中常被采用。

串的塊鏈存儲表示

為了提高空間利用率，可使每個結點存放多個字符（這是順序串和鏈串的綜合 (折衷) ），稱為塊鏈結構。

?優點：便于插入和刪除 ? ?缺點：空間利用率低?

串的定長表示

思想和代碼都不難，和線性表也差不多，串本來就是數據受限的線性表。

串連接：

#include <stdio.h>
#include <string.h>
//串的定長順序存儲表示
#define MAXSTRLEN 255							//用戶可在255以內定義最大串長
typedef unsigned char SString[MAXSTRLEN + 1];	//0號單元存放串的長度int Concat(SString *T,SString S1,SString S2)//用T返回S1和S2聯接而成的新串。若未截斷返回1，若截斷返回0
{int i = 1,j,uncut = 0;if(S1[0] + S2[0] <= MAXSTRLEN)	//未截斷{for (i = 1; i <= S1[0]; i++)//賦值時等號不可丟(*T)[i] = S1[i];for (j = 1; j <= S2[0]; j++)(*T)[S1[0]+j] = S2[j];	//(*T)[i+j] = S2[j](*T)[0] = S1[0] + S2[0];uncut = 1;}else if(S1[0] < MAXSTRLEN)		//截斷{for (i = 1; i <= S1[0]; i++)//賦值時等號不可丟(*T)[i] = S1[i];for (j = S1[0] + 1; j <= MAXSTRLEN; j++){(*T)[j] = S2[j - S1[0] ];(*T)[0] = MAXSTRLEN;uncut = 0;}}else{for (i = 0; i <= MAXSTRLEN; i++)(*T)[i] = S1[i];/*或者分開賦值，先賦值內容，再賦值長度for (i = 1; i <= MAXSTRLEN; i++)(*T)[i] = S1[i];(*T)[0] = MAXSTRLEN;*/uncut = 0;}return uncut;
}int SubString(SString *Sub,SString S,int pos,int len)//用Sub返回串S的第pos個字符起長度為len的子串//其中，1 ≤ pos ≤ StrLength(S)且0 ≤ len ≤ StrLength(S) - pos + 1(從pos開始到最后有多少字符)//第1個字符的下標為1,因為第0個字符存放字符長度
{int i;if(pos < 1 || pos > S[0] || len < 0 || len > S[0] - pos + 1)return 0;for (i = 1; i <= len; i++){//S中的[pos,len]的元素 -> *Sub中的[1,len](*Sub)[i] = S[pos + i - 1];//下標運算符 > 尋址運算符的優先級}(*Sub)[0] = len;return 1;
}
void PrintStr(SString S)
{int i;for (i = 1; i <= S[0]; i++)printf("%c",S[i]);printf("\n");
}int main(void)
{/*定長順序存儲初始化和打印的方法SString s = {4,'a','b','c','d'};int i;//s = "abc";	//不可直接賦值for (i = 1; i <= s[0]; i++)printf("%c",s[i]);*/SString s1 = {4,'a','b','c','d'};SString s2 = {4,'e','f','g','h'},s3;SString T,Sub;int i;for (i = 1; i <= 255; i++){s3[i] = 'a';if(i >= 248)s3[i] = 'K';}s3[0] = 255;SubString(&Sub,s3,247,8);PrintStr(Sub);return 0;
}

第九次筆記（數組，廣義表）

數組：按一定格式排列起來的具有相同類型的數據元素的集合。

二維數組：若一維數組中的數據元素又是一維數組結構，則稱為二維數組。?

同理，推廣到多維數組。若 n -1 維數組中的元素又是一個一維數組結構，則稱作 n 維數組。?

聲明格式：數據類型 ? 變量名稱[行數] [列數] ；

實現：一般都是采用順序存儲結構來表示數組。

二維數組兩種順序存儲方式：以行序為主序 (低下標優先) 、以列序為主序 (高下標優先)

一個二維數組 A，行下標的范圍是 1 到 6，列下標的范圍是 0 到 7，每個數組元素用相鄰的6 個字節存儲，存儲器按字節編址。那么，這個數組的體積是288個字節。

?廣義表（又稱列表 Lists）是n≥0個元素 a1, a2, …, an 的有限序列，其中每一個ai 或者是原子，或者是一個子表。

表頭：若 LS 非空 (n≥1 )，則其第一個元素 a1 就是表頭。

?表尾：除表頭之外的其它元素組成的表。記作 ?tail(LS) = (a2, ..., an)。?

(( ))?長度為 1，表頭、表尾均為 ( )

(a, (b, c))長度為 2，由原子 a 和子表 (b, c) 構成。表頭為 a ；表尾為 ((b, c))。

廣義表的長度定義為最外層所包含元素的個數

廣義表的深度定義為該廣義表展開后所含括號的重數。

“原子”的深度為 0 ; ?“空表”的深度為 1 。

取表頭運算 GetHead ?和取表尾運算 GetTail

GetHead(LS) = a1 ? ? ? ?GetTail(LS) = (a2, …, an)。

廣義表可看成是線性表的推廣，線性表是廣義表的特例。

廣義表的結構相當靈活，在某種前提下，它可以兼容線性表、數組、樹和有向圖等各種常用的數據結構。

由于廣義表不僅集中了線性表、數組、樹和有向圖等常見數據結構的特點，而且可有效地利用存儲空間，因此在計算機的許多應用領域都有成功使用廣義表的實例。?

第十次筆記（樹和二叉樹）

樹

樹的定義：樹(Tree)是 n(n≥0)個結點的有限集。若 n=0，稱為空樹；若 n > 0，則它滿足如下兩個條件： ?

(1) ?有且僅有一個特定的稱為根 (Root) 的結點； ?

(2) ?其余結點可分為 m (m≥0) 個互不相交的有限集 T1, T2, T3, …, Tm，其中每一個集合本身又是一棵樹，并稱為根的子樹 (SubTree)。

顯然，樹的定義是一個遞歸的定義。

樹的一些術語：

結點的度（Degree）：結點的子樹個數；
樹的度：樹的所有結點中最大的度數；
葉結點（Leaf）：度為0的結點；
父結點（Parent）：有子樹的結點是其子樹的根節點的父結點；
子結點/孩子結點（Child）：若A結點是B結點的父結點，則稱B結點是A結點的子結點；
兄弟結點（Sibling）：具有同一個父結點的各結點彼此是兄弟結點；
路徑和路徑長度：從結點n1到nk的路徑為一個結點序列n1，n2，...，nk。ni是ni+1的父結點。路徑所包含邊的個數為路徑的長度；
祖先結點（Ancestor）：沿樹根到某一結點路徑上的所有結點都是這個結點的祖先結點；
子孫結點（Descendant）：某一結點的子樹中的所有結點是這個結點的子孫；
結點的層次（Level）：規定根結點在1層，其他任一結點的層數是其父結點的層數加1；
樹的深度（Depth）：樹中所有結點中的最大層次是這棵樹的深度；

將樹中節點的各子樹看成從左至右是有次序的（即不能互換），則稱為該樹是有序樹，否則稱為無序樹。

森林(forest)是 m (m≥0) 棵互不相交的樹的集合。

?

二叉樹

在計算機科學中，二叉樹是每個結點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”（left subtree）和“右子樹”（right subtree）。二叉樹常被用于實現二叉查找樹和二叉堆。

雖然二叉樹與樹概念不同，但有關樹的基本術語對二叉樹都適用。

二叉樹結點的子樹要區分左子樹和右子樹，即使只有一棵子樹也要進行區分，說明它是左子樹，還是右子樹。樹當結點只有一個孩子時，就無須區分它是左還是右。

注意：盡管二叉樹與樹有許多相似之處，但二叉樹不是樹的特殊情形。

一些性質：

在二叉樹的第 i 層上至多有? 個結點 (i ≥1)。

證明：每個節點至多兩個孩子，每一層至多比上一層多一倍的結點，根為1.

深度為 k 的二叉樹至多有個結點（k ≥1)。

證明：把每一層最大節點加起來即可

對任何一棵二叉樹 T，如果其葉子數為 n0，度為 2的結點數為 n2，則 n0 = n2 + 1。

證明：對于一個只有根的樹，n0 = n2 + 1成立。1=0+1

我們把一個葉子節點換成度為2的結點：

黑色節點原來為葉子節點

我們發現，度為2的結點數加1（黑色節點）；葉子節點數加1（原來的去掉，新增兩個）；對于式子n0 = n2 + 1沒影響，還是成立。

我們把葉子節點換成度為1的結點，比如沒有右孩子。

我們發現，度為2的結點數沒變。葉子節點數沒變（減了一個加了一個）

所以，不管你怎么換，公式都成立。（佛系證明）

二叉樹概述

各種實現和應用以后放鏈接

一、二叉樹的基本概念

二叉樹：二叉樹是每個節點最多有兩個子樹的樹結構。

根節點：一棵樹最上面的節點稱為根節點。

父節點、子節點：如果一個節點下面連接多個節點，那么該節點稱為父節點，它下面的節點稱為子節點。

葉子節點：沒有任何子節點的節點稱為葉子節點。

兄弟節點：具有相同父節點的節點互稱為兄弟節點。

節點度：節點擁有的子樹數。上圖中，13的度為2，46的度為1，28的度為0。

樹的深度：從根節點開始（其深度為0）自頂向下逐層累加的。上圖中，13的深度是1，30的深度是2，28的深度是3。

樹的高度：從葉子節點開始（其高度為0）自底向上逐層累加的。54的高度是2，根節點23的高度是3。

對于樹中相同深度的每個節點來說，它們的高度不一定相同，這取決于每個節點下面的葉子節點的深度。上圖中，13和54的深度都是1，但是13的高度是1，54的高度是2。

二、二叉樹的類型

類型	定義	圖示
滿二叉樹 Full Binary Tree	除最后一層無任何子節點外，每一層上的所有節點都有兩個子節點，最后一層都是葉子節點。滿足下列性質： 1）一顆樹深度為h，最大層數為k，深度與最大層數相同，k=h； 2）葉子節點數（最后一層）為2k?1； 3）第 i 層的節點數是：2i?1； 4）總節點數是：2k?1，且總節點數一定是奇數。
完全二叉樹 Complete Binary Tree	若設二叉樹的深度為h，除第 h 層外，其它各層 (1～h-1) 的結點數都達到最大個數，第 h 層所有的結點都連續集中在最左邊，這就是完全二叉樹。滿足下列性質： 1）只允許最后一層有空缺結點且空缺在右邊，即葉子節點只能在層次最大的兩層上出現； 2）對任一節點，如果其右子樹的深度為j，則其左子樹的深度必為j或j+1。即度為1的點只有1個或0個； 3）除最后一層，第 i 層的節點數是：2i?1； 4）有n個節點的完全二叉樹，其深度為：log2n+1或為log2n+1； 5）滿二叉樹一定是完全二叉樹，完全二叉樹不一定是滿二叉樹。
平衡二叉樹 Balanced Binary Tree	又被稱為AVL樹，它是一顆空樹或左右兩個子樹的高度差的絕對值不超過 1，并且左右兩個子樹都是一棵平衡二叉樹。
二叉搜索樹 Binary Search Tree	又稱二叉查找樹、二叉排序樹（Binary Sort Tree）。它是一顆空樹或是滿足下列性質的二叉樹： 1）若左子樹不空，則左子樹上所有節點的值均小于或等于它的根節點的值； 2）若右子樹不空，則右子樹上所有節點的值均大于或等于它的根節點的值； 3）左、右子樹也分別為二叉排序樹。
紅黑樹 Red Black Tree	是每個節點都帶有顏色屬性（顏色為紅色或黑色）的自平衡二叉查找樹，滿足下列性質： 1）節點是紅色或黑色； 2）根節點是黑色； 3）所有葉子節點都是黑色； 4）每個紅色節點必須有兩個黑色的子節點。(從每個葉子到根的所有路徑上不能有兩個連續的紅色節點。) 5）從任一節點到其每個葉子的所有簡單路徑都包含相同數目的黑色節點。

啦啦啦

第十一次筆記（滿二叉樹，完全二叉樹）

因為圖片丟失，內容不全，我盡量找一下圖

滿二叉樹 (Full binary tree)

除最后一層無任何子節點外，每一層上的所有結點都有兩個子結點二叉樹。

國內教程定義：一個二叉樹，如果每一個層的結點數都達到最大值，則這個二叉樹就是滿二叉樹。也就是說，如果一個二叉樹的層數為K，且結點總數是(2^k) -1 ，則它就是滿二叉樹。

國外(國際)定義:a binary tree T is full if each node is either a leaf or possesses exactly two childnodes.

大意為：如果一棵二叉樹的結點要么是葉子結點，要么它有兩個子結點，這樣的樹就是滿二叉樹。(一棵滿二叉樹的每一個結點要么是葉子結點，要么它有兩個子結點，但是反過來不成立，因為完全二叉樹也滿足這個要求，但不是滿二叉樹)

從圖形形態上看，滿二叉樹外觀上是一個三角形。

~~這里缺失公式~~

完全二叉樹

完全二叉樹是效率很高的數據結構，完全二叉樹是由滿二叉樹而引出來的。對于深度為K的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。

可以根據公式進行推導，假設n0是度為0的結點總數（即葉子結點數），n1是度為1的結點總數，n2是度為2的結點總數，則：

①n= n0+n1+n2?（其中n為完全二叉樹的結點總數）；又因為一個度為2的結點會有2個子結點，一個度為1的結點會有1個子結點，除根結點外其他結點都有父結點，

②n= 1+n1+2*n2?；由①、②兩式把n2消去得：n= 2*n0+n1-1，由于完全二叉樹中度為1的結點數只有兩種可能0或1，由此得到n0=n/2 或 n0=(n+1)/2。

簡便來算，就是 n0=n/2，其中n為奇數時（n1=0）向上取整；n為偶數時（n1=1）。可根據完全二叉樹的結點總數計算出葉子結點數。

重點：出于簡便起見,完全二叉樹通常采用數組而不是鏈表存儲

對于tree[i]，有如下特點：

（1）若i為奇數且i>1，那么tree的左兄弟為tree[i-1]；

（2）若i為偶數且i<n，那么tree的右兄弟為tree[i+1]；

（3）若i>1，tree的父親節點為tree[i?div?2]；

（4）若2*i<=n，那么tree的左孩子為tree[2*i]；若2*i+1<=n，那么tree的右孩子為tree[2*i+1]；

（5）若i>n div 2,那么tree[i]為葉子結點（對應于（3））；

（6）若i<(n-1) div 2.那么tree[i]必有兩個孩子（對應于（4））。

（7）滿二叉樹一定是完全二叉樹，完全二叉樹不一定是滿二叉樹。

完全二叉樹第i層至多有2^（i-1）個節點，共i層的完全二叉樹最多有2^i-1個節點。

特點：

1）只允許最后一層有空缺結點且空缺在右邊，即葉子結點只能在層次最大的兩層上出現；

2）對任一結點，如果其右子樹的深度為j，則其左子樹的深度必為j或j+1。即度為1的點只有1個或0個

第十二次筆記（二叉樹的存儲和遍歷）

順序存儲結構

完全二叉樹：用一組地址連續的存儲單元依次自上而下、自左至右存儲結點元素，即將編號為 i ?的結點元素存儲在一維數組中下標為 i –1 的分量中。

一般二叉樹：將其每個結點與完全二叉樹上的結點相對照，存儲在一維數組的相應分量中。

最壞情況：樹退化為線性后：

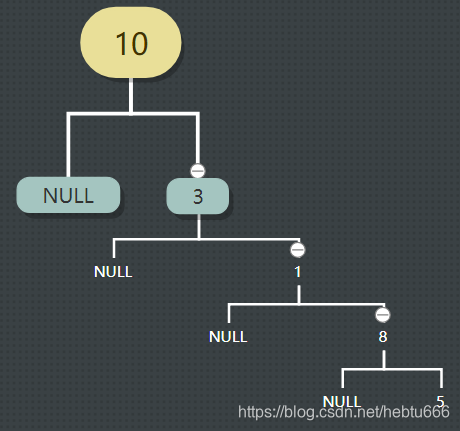
我們要把它“變”成這個大家伙來存了：

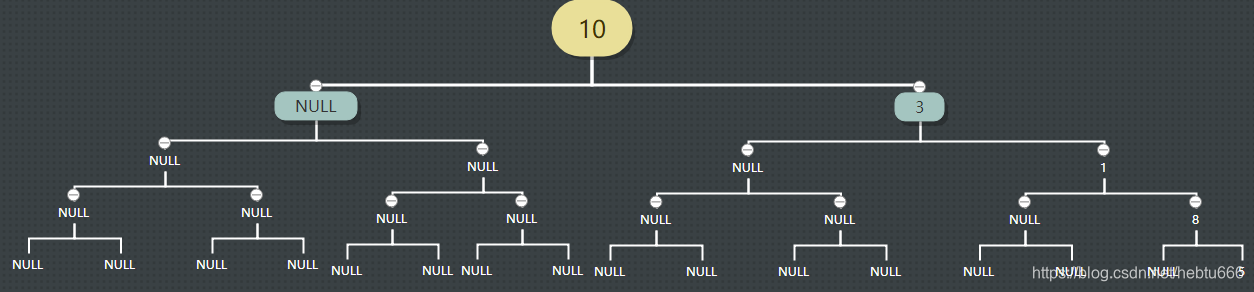
深度為 k 的且只有 k 個結點的右單支樹需要長度為2^k-1 的一維數組。?

鏈式存儲結構

lchild和rchild都是指向相同結構的指針

在 n 個結點的二叉鏈表中有 n + 1 個空指針域。

typedef struct BiTNode { // 結點結構TElemType data;struct BiTNode *lchild,*rchild;// 左右孩子指針
} BiTNode, *BiTree;

可以多一條指向父的指針。

遍歷二叉樹

順著某一條搜索路徑巡訪二叉樹中的結點，使 ? 得每個結點均被訪問一次，而且僅被訪問一次

?“訪問”的含義很廣，可以是對結點作各種處理，如：輸出結點的信息、修改結點的數據值等，但要求這種訪問不破壞原來的數據結構。

（所以有些題目比如morris遍歷、鏈表后半段反轉判斷回文等等必須進行完，解題時就算已經得出答案也要遍歷完，因為我們不能改變原來的數據結構。）

具體遍歷的介紹

https://blog.csdn.net/hebtu666/article/details/82853988

深入理解二叉樹遍歷

二叉樹：二叉樹是每個節點最多有兩個子樹的樹結構。

本文介紹二叉樹的遍歷相關知識。

我們學過的基本遍歷方法，無非那么幾個：前序，中序，后序，還有按層遍歷等等。

設L、D、R分別表示遍歷左子樹、訪問根結點和遍歷右子樹，則對一棵二叉樹的遍歷有三種情況：DLR（稱為先根次序遍歷），LDR（稱為中根次序遍歷），LRD （稱為后根次序遍歷）。

首先我們定義一顆二叉樹

typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{ElementType Data;BinTree Left;BinTree Right;
};

前序

首先訪問根，再先序遍歷左（右）子樹，最后先序遍歷右（左）子樹

思路：

就是利用函數，先打印本個節點，然后對左右子樹重復此過程即可。

void PreorderTraversal( BinTree BT )
{if(BT==NULL)return ;printf(" %c", BT->Data);PreorderTraversal(BT->Left);PreorderTraversal(BT->Right);
}

中序

首先中序遍歷左（右）子樹，再訪問根，最后中序遍歷右（左）子樹

思路：

還是利用函數，先對左邊重復此過程，然后打印根，然后對右子樹重復。

void InorderTraversal( BinTree BT )
{if(BT==NULL)return ;InorderTraversal(BT->Left);printf(" %c", BT->Data);InorderTraversal(BT->Right);
}

后序

首先后序遍歷左（右）子樹，再后序遍歷右（左）子樹，最后訪問根

思路：

先分別對左右子樹重復此過程，然后打印根

void PostorderTraversal(BinTree BT)
{if(BT==NULL)return ;PostorderTraversal(BT->Left);PostorderTraversal(BT->Right);printf(" %c", BT->Data);
}

進一步思考

看似好像很容易地寫出了三種遍歷。。。。。

但是你真的理解為什么這么寫嗎？

比如前序遍歷，我們真的是按照定義里所講的，首先訪問根，再先序遍歷左（右）子樹，最后先序遍歷右（左）子樹。這種過程來遍歷了一遍二叉樹嗎？

仔細想想，其實有一絲不對勁的。。。

再看代碼：

void Traversal(BinTree BT)//遍歷
{
//1111111111111Traversal(BT->Left);
//22222222222222Traversal(BT->Right);
//33333333333333
}

為了敘述清楚，我給三個位置編了號?1，2，3

我們憑什么能前序遍歷，或者中序遍歷，后序遍歷？

我們看，前序中序后序遍歷，實現的代碼其實是類似的，都是上面這種格式，只是我們分別在位置1，2，3打印出了當前節點而已啊。我們憑什么認為，在1打印，就是前序，在2打印，就是中序，在3打印，就是后序呢？不管在位置1，2，3哪里操作，做什么操作，我們利用函數遍歷樹的順序變過嗎？當然沒有啊。。。

都是三次返回到當前節點的過程：先到本個節點，也就是位置1，然后調用了其他函數，最后調用完了，我們開到了位置2。然后又調用別的函數，調用完了，我們來到了位置3.。然后，最后操作完了，這個函數才結束。代碼里的三個位置，每個節點都被訪問了三次。

而且不管位置1，2，3打印了沒有，操作了沒有，這個順序是永遠存在的，不會因為你在位置1打印了，順序就改為前序，你在位置2打印了，順序就成了中序。

為了有更直觀的印象，我們做個試驗：在位置1，2，3全都放入打印操作；

我們會發現，每個節點都被打印了三次。而把每個數第一次出現拿出來，就組成了前序遍歷的序列；所有數字第二次出現拿出來，就組成了中序遍歷的序列。。。。

其實，遍歷是利用了一種數據結構：棧

而我們這種寫法，只是通過函數，來讓系統幫我們壓了棧而已。為什么能實現遍歷？為什么我們訪問完了左子樹，能返回到當前節點？這都是棧的功勞啊。我們把當前節點（對于函數就是當時的現場信息）存到了棧里，記錄下來，后來才能把它拿了出來，能回到以前的節點。

想到這里，可能就有更深刻的理解了。

我們能否不用函數，不用系統幫我們壓棧，而是自己做一個棧，來實現遍歷呢？

先序實現思路：拿到一個節點的指針，先判斷是否為空，不為空就先訪問（打印）該結點，然后直接進棧，接著遍歷左子樹；為空則要從棧中彈出一個節點來，這個時候彈出的結點就是其父親，然后訪問其父親的右子樹，直到當前節點為空且棧為空時，結束。

核心思路代碼實現：

*p=root;
while(p || !st.empty())
{if(p)//非空{//visit(p);進行操作st.push(p);//入棧p = p->lchild;左} else//空{p = st.top();//取出st.pop();p = p->rchild;//右}
}

中序實現思路：和前序遍歷一樣，只不過在訪問節點的時候順序不一樣，訪問節點的時機是從棧中彈出元素時訪問，如果從棧中彈出元素，就意味著當前節點父親的左子樹已經遍歷完成，這時候訪問父親，就是中序遍歷.

（對應遞歸是第二次遇到）

核心代碼實現：

*p=root;
while(p || !st.empty())
{if(p)//非空{st.push(p);//壓入p = p->lchild;}else//空{p = st.top();//取出//visit(p);操作st.pop();p = p->rchild;}
}

后序遍歷是最難的。因為要保證左孩子和右孩子都已被訪問并且左孩子在右孩子前訪問才能訪問根結點，這就為流程的控制帶來了難點。

因為我們原來說了，后序是第三次遇到才進行操作的，所以我們很容易有這種和遞歸函數類似的思路：對于任一結點，將其入棧，然后沿其左子樹一直往下走，一直走到沒有左孩子的結點，此時該結點在棧頂，但是不能出棧訪問，因此右孩子還沒訪問。所以接下來按照相同的規則對其右子樹進行相同的處理。訪問完右孩子，該結點又出現在棧頂，此時可以將其出棧并訪問。這樣就保證了正確的訪問順序。可以看出，在這個過程中，每個結點都兩次出現在棧頂，只有在第二次出現在棧頂時，才能訪問它。因此需要多設置一個變量標識該結點是否是第一次出現在棧頂。

第二種思路：對于任一結點P，先將其入棧。如果P不存在左孩子和右孩子，或者左孩子和右孩子都已被訪問過了，就可以直接訪問該結點。如果有孩子未訪問，將P的右孩子和左孩子依次入棧。

網上的思路大多是第一種，所以我在這里給出第二種的大概實現吧

首先初始化cur，pre兩個指針，代表訪問的當前節點和之前訪問的節點。把根放入，開始執行。

s.push(root);
while(!s.empty())
{cur=s.top();if((cur->lchild==NULL && cur->rchild==NULL)||(pre!=NULL && (pre==cur->lchild||pre==cur->rchild))){//visit(cur);  如果當前結點沒有孩子結點或者孩子節點都已被訪問過 s.pop();//彈出pre=cur; //記錄}else//分別放入右左孩子{if(cur->rchild!=NULL)s.push(cur->rchild);if(cur->lchild!=NULL)    s.push(cur->lchild);}
}

這兩種方法，都是利用棧結構來實現的遍歷，需要一定的棧空間，而其實存在一種時間O(N),空間O(1)的遍歷方式，下次寫了我再放鏈接。

斗個小機靈：后序是LRD，我們其實已經知道先序是DLR，那其實我們可以用先序來實現后序啊，我們只要先序的時候把左右子樹換一下：DRL（這一步很好做到），然后倒過來不就是DRL了嘛。。。。。就把先序代碼改的左右反過來，然后放棧里倒過來就好了，不需要上面介紹的那些復雜的方法。。。。

第十四次筆記（樹的存儲）

父節點表示法

數據域：存放結點本身信息。

雙親域：指示本結點的雙親結點在數組中的位置。

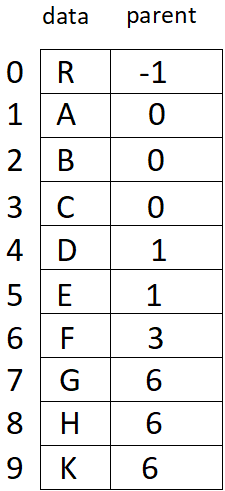
對應的樹：

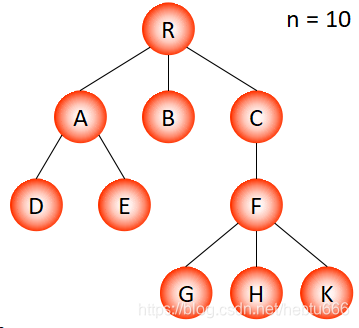
/* 樹節點的定義 */
#define MAX_TREE_SIZE 100typedef struct{TElemType data;int parent; /* 父節點位置域 */
} PTNode;typedef struct{PTNode nodes[MAX_TREE_SIZE];int n; /* 節點數 */
} PTree;

特點：找雙親容易，找孩子難。

孩子表示法（樹的鏈式存儲結構）

childi指向一個結點

可以加上parent。

在有 n 個結點、度為 ?d 的樹的 d 叉鏈表中，有 ?n×(d－1)＋1 個空鏈域

我們可以用degree記錄有幾個孩子，省掉空間，但是結點的指針個數不相等，為該結點的度 degree。

孩子鏈表：

把每個結點的孩子結點排列起來，看成是一個線性表，用單鏈表存儲，則 n 個結點有 n 個孩子鏈表（葉子的孩子鏈表為空表）。而 n 個頭指針又組成一個線性表，用順序表（含 n 個元素的結構數組）存儲。

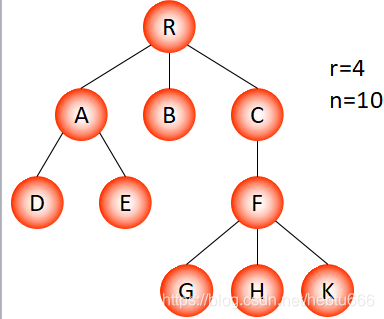
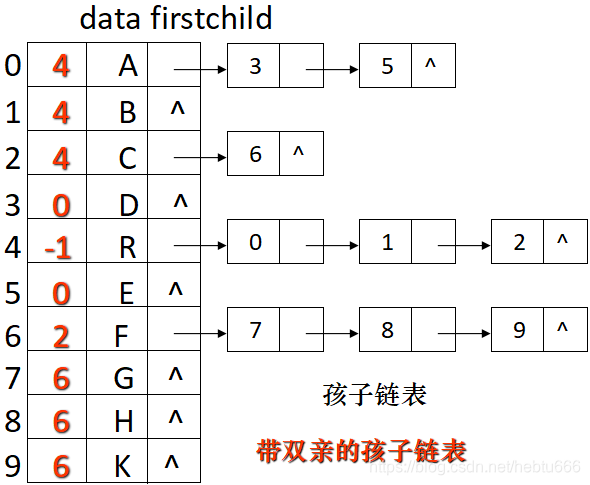
孩子兄弟表示法（二叉樹表示法）

用二叉鏈表作樹的存儲結構，鏈表中每個結點的兩個指針域分別指向其第一個孩子結點和下一個兄弟結點

typedef struct CSNode{ElemType data;struct CSNode *firstchild, *nextsibling;  
} CSNode, *CSTree;

第十五次筆記（圖基礎）

圖是一種： ? 數據元素間存在多對多關系的數據結構 ? 加上一組基本操作構成的抽象數據類型。

圖 (Graph) 是一種復雜的非線性數據結構，由頂點集合及頂點間的關系（也稱弧或邊）集合組成。可以表示為： G＝(V, VR) ?

其中 V 是頂點的有窮非空集合；

VR 是頂點之間 ? 關系的有窮集合，也叫做弧或邊集合。

弧是頂點的有序對，邊是頂點的無序對。

特點：（相對于線性結構）

頂點之間的關系是任意的?

圖中任意兩個頂點之間都可能相關

頂點的前驅和后繼個數無限制

圖的存儲

多重鏈表：完全模擬圖的樣子，每個節點內的指針都指向該指向的節點。

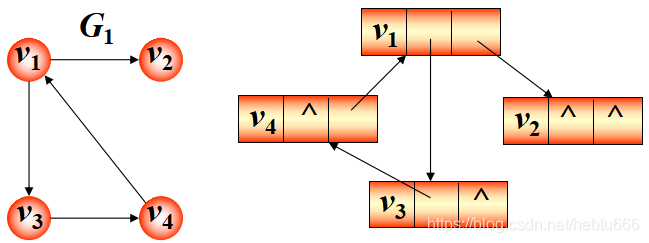
節點結構內指針數為度

缺點：浪費空間、不容易操作

數組表示法（鄰接矩陣表示法）

可用兩個數組存儲。其中一個一維數組存儲數據元素（頂點）的信息，另一個二維數組（鄰接矩陣）存儲數據元素之間的關系（邊或弧）的信息

有向圖：

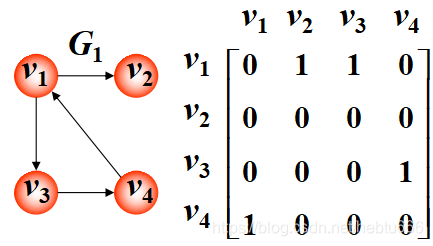
有向網：

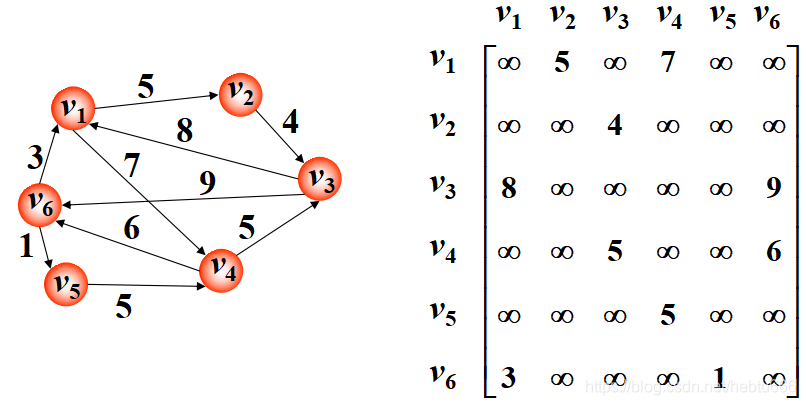
缺點：用于稀疏圖時空間浪費嚴重

優點：操作較容易

鄰接表

指針數組存放每個結點，每個結點后接所有能到達的節點。

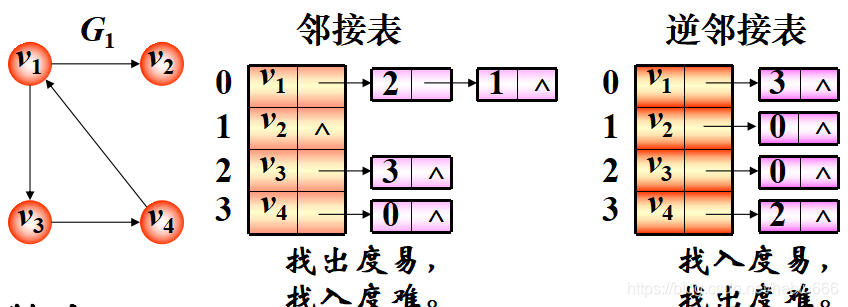
圖的遍歷

從圖的任意指定頂點出發，依照某種規則去訪問圖中所有頂點，且每個頂點僅被訪問一次，這一過程叫做圖的遍歷。

圖的遍歷按照深度優先和廣度優先規則去實施，通常有深度優先遍歷法（Depth_First Search——DFS ）和 ?廣度優先遍歷法（ Breadth_Frist Search——BFS）兩種。

簡單棋盤搜索https://blog.csdn.net/hebtu666/article/details/81483407

別的實現以后再貼

如何判別V的鄰接點是否被訪問？

為每個頂點設立一個“訪問標志”。

最小生成樹

問題提出：
????要在n個城市間建立通信聯絡網。頂點：表示城市，權：城市間通信線路的花費代價。希望此通信網花費代價最小。
問題分析：
????答案只能從生成樹中找，因為要做到任何兩個城市之間有線路可達，通信網必須是連通的；但對長度最小的要求可以知道網中顯然不能有圈，如果有圈，去掉一條邊后，并不破壞連通性，但總代價顯然減少了，這與總代價最小的假設是矛盾的。
結論：
????希望找到一棵生成樹，它的每條邊上的權值之和（即建立該通信網所需花費的總代價）最小 —— 最小代價生成樹。
????構造最小生成樹的算法很多，其中多數算法都利用了一種稱之為 MST 的性質。
????MST 性質：設 N = (V, E) ?是一個連通網，U是頂點集 V的一個非空子集。若邊 (u, v) 是一條具有最小權值的邊，其中u∈U，v∈V-U，則必存在一棵包含邊 (u, v) 的最小生成樹。

（1）普里姆 (Prim) 算法

算法思想：?
????①設 N=(V, E)是連通網，TE是N上最小生成樹中邊的集合。
????②初始令 U={u_0}, (u_0∈V), TE={ }。
????③在所有u∈U，u∈U-V的邊(u,v)∈E中，找一條代價最小的邊(u_0,v_0 )。
????④將(u_0,v_0 )并入集合TE，同時v_0并入U。
????⑤重復上述操作直至U = V為止，則 T=(V,TE)為N的最小生成樹。

?
代碼實現：

void MiniSpanTree_PRIM(MGraph G,VertexType u)//用普里姆算法從第u個頂點出發構造網G的最小生成樹T，輸出T的各條邊。//記錄從頂點集U到V-U的代價最小的邊的輔助數組定義；//closedge[j].lowcost表示在集合U中頂點與第j個頂點對應最小權值
{int k, j, i;k = LocateVex(G,u);for (j = 0; j < G.vexnum; ++j)?? ?//輔助數組的初始化if(j != k){closedge[j].adjvex = u;closedge[j].lowcost = G.arcs[k][j].adj;?? ?
//獲取鄰接矩陣第k行所有元素賦給closedge[j!= k].lowcost}closedge[k].lowcost = 0;?? ??? ?
//初始，U = {u}; ?PrintClosedge(closedge,G.vexnum);for (i = 1; i < G.vexnum; ++i)?? ?\
//選擇其余G.vexnum-1個頂點，因此i從1開始循環{k = minimum(G.vexnum,closedge);?? ??? ?
//求出最小生成樹的下一個結點：第k頂點PrintMiniTree_PRIM(G, closedge, k); ?? ?//輸出生成樹的邊closedge[k].lowcost = 0;?? ??? ??? ??? ?//第k頂點并入U集PrintClosedge(closedge,G.vexnum);for(j = 0;j < G.vexnum; ++j){ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??if(G.arcs[k][j].adj < closedge[j].lowcost)?? ?
//比較第k個頂點和第j個頂點權值是否小于closedge[j].lowcost{closedge[j].adjvex = G.vexs[k];//替換closedge[j]closedge[j].lowcost = G.arcs[k][j].adj;PrintClosedge(closedge,G.vexnum);}}}
}

（2）克魯斯卡爾 (Kruskal) 算法

算法思想：?
????①設連通網 ?N = (V, E )，令最小生成樹初始狀態為只有n個頂點而無邊的非連通圖，T=(V, { })，每個頂點自成一個連通分量。
????②在 E 中選取代價最小的邊，若該邊依附的頂點落在T中不同的連通分量上（即：不能形成環），則將此邊加入到T中；否則，舍去此邊，選取下一條代價最小的邊。
③依此類推，直至 T 中所有頂點都在同一連通分量上為止。
??????
????最小生成樹可能不惟一！

拓撲排序

（1）有向無環圖

????無環的有向圖，簡稱 DAG (Directed Acycline Graph) 圖。
?
有向無環圖在工程計劃和管理方面的應用：除最簡單的情況之外，幾乎所有的工程都可分為若干個稱作“活動”的子工程，并且這些子工程之間通常受著一定條件的約束，例如：其中某些子工程必須在另一些子工程完成之后才能開始。
對整個工程和系統，人們關心的是兩方面的問題：?
①工程能否順利進行；?
②完成整個工程所必須的最短時間。
對應到有向圖即為進行拓撲排序和求關鍵路徑。?
AOV網：?
????用一個有向圖表示一個工程的各子工程及其相互制約的關系，其中以頂點表示活動，弧表示活動之間的優先制約關系，稱這種有向圖為頂點表示活動的網，簡稱AOV網(Activity On Vertex network)。
例如：排課表
??????
AOV網的特點：
①若從i到j有一條有向路徑，則i是j的前驅；j是i的后繼。
②若< i , j >是網中有向邊，則i是j的直接前驅；j是i的直接后繼。
③AOV網中不允許有回路，因為如果有回路存在，則表明某項活動以自己為先決條件，顯然這是荒謬的。

問題： ???
????問題：如何判別 AOV 網中是否存在回路？
????檢測 AOV 網中是否存在環方法：對有向圖構造其頂點的拓撲有序序列，若網中所有頂點都在它的拓撲有序序列中，則該AOV網必定不存在環。

拓撲排序的方法：
????①在有向圖中選一個沒有前驅的頂點且輸出之。
????②從圖中刪除該頂點和所有以它為尾的弧。
????③重復上述兩步，直至全部頂點均已輸出；或者當圖中不存在無前驅的頂點為止。
????????
????一個AOV網的拓撲序列不是唯一的！
代碼實現：

Status TopologicalSort(ALGraph G)//有向圖G采用鄰接表存儲結構。//若G無回路，則輸出G的頂點的一個拓撲序列并返回OK，否則返回ERROR.//輸出次序按照棧的后進先出原則，刪除頂點，輸出遍歷
{SqStack S;int i, count;int *indegree1 = (int *)malloc(sizeof(int) * G.vexnum);int indegree[12] = {0};FindInDegree(G, indegree);?? ?//求個頂點的入度下標從0開始InitStack(&S);PrintStack(S);for(i = 0; i < G.vexnum; ++i)if(!indegree[i])?? ??? ?//建0入度頂點棧Spush(&S,i);?? ??? ?//入度為0者進棧count = 0;?? ??? ??? ??? ?//對輸出頂點計數while (S.base != S.top){ArcNode* p;pop(&S,&i);VisitFunc(G,i);//第i個輸出棧頂元素對應的頂點，也就是最后進來的頂點?? ?++count;?? ??? ? ?//輸出i號頂點并計數for(p = G.vertices[i].firstarc; p; p = p->nextarc){?? ?//通過循環遍歷第i個頂點的表結點，將表結點中入度都減1int k = p->adjvex;?? ?//對i號頂點的每個鄰接點的入度減1if(!(--indegree[k]))push(&S,k);?? ??? ?//若入度減為0，則入棧}//for}//whileif(count < G.vexnum){printf("\n該有向圖有回路!\n");return ERROR;?? ?//該有向圖有回路}else{printf("\n該有向圖沒有回路!\n");return OK;}
}

關鍵路徑

????把工程計劃表示為有向圖，用頂點表示事件，弧表示活動，弧的權表示活動持續時間。每個事件表示在它之前的活動已經完成，在它之后的活動可以開始。稱這種有向圖為邊表示活動的網，簡稱為 AOE網 (Activity On Edge)。
例如：
設一個工程有11項活動，9個事件。
事件v_1——表示整個工程開始（源點）?
事件v_9——表示整個工程結束（匯點）

?
對AOE網，我們關心兩個問題： ?
①完成整項工程至少需要多少時間？?
②哪些活動是影響工程進度的關鍵？
關鍵路徑——路徑長度最長的路徑。
路徑長度——路徑上各活動持續時間之和。
v_i——表示事件v_i的最早發生時間。假設開始點是v_1，從v_1到〖v�i〗的最長路徑長度。?(?)——表示活動a_i的最早發生時間。
l(?)——表示活動a_i最遲發生時間。在不推遲整個工程完成的前提下，活動a_i最遲必須開始進行的時間。
l(?)-?(?)意味著完成活動a_i的時間余量。
我們把l(?)=?(?)的活動叫做關鍵活動。顯然，關鍵路徑上的所有活動都是關鍵活動，因此提前完成非關鍵活動并不能加快工程進度。
????例如上圖中網，從從v_1到v_9的最長路徑是(v_1,v_2,v_5,v_8,ν_9 )，路徑長度是18，即ν_9的最遲發生時間是18。而活動a_6的最早開始時間是5，最遲開始時間是8，這意味著：如果a_6推遲3天或者延遲3天完成，都不會影響整個工程的完成。因此，分析關鍵路徑的目的是辨別哪些是關鍵活動，以便爭取提高關鍵活動的工效，縮短整個工期。
????由上面介紹可知：辨別關鍵活動是要找l(?)=?(?)的活動。為了求?(?)和l(?)，首先應求得事件的最早發生時間v?(j)和最遲發生時間vl(j)。如果活動a_i由弧?j,k?表示，其持續時間記為dut(?j,k?),則有如下關系：
?(?)= v?(j)
l(?)=vl(k)-dut(?j,k?)
????求v?(j)和vl(j)需分兩步進行：
第一步：從v?(0)=0開始向前遞推
v?(j)=Max{v?(i)+dut(?j,k?)} ???i,j?∈T,j=1,2,…,n-1
其中，T是所有以第j個頂點為頭的弧的集合。
第二步：從vl(n-1)=v?(n-1)起向后遞推
vl(i)=Min{vl(j)-dut(?i,j?)} ??i,j?∈S,i=n-2,…,0
其中，S是所有以第i個頂點為尾的弧的集合。
下面我們以上圖AOE網為例，先求每個事件v_i的最早發生時間，再逆向求每個事件對應的最晚發生時間。再求每個活動的最早發生時間和最晚發生時間，如下面表格：
??????????
在活動的統計表中，活動的最早發生時間和最晚發生時間相等的，就是關鍵活動

關鍵路徑的討論：

①若網中有幾條關鍵路徑，則需加快同時在幾條關鍵路徑上的關鍵活動。 ?????如：a11、a10、a8、a7。?
②如果一個活動處于所有的關鍵路徑上，則提高這個活動的速度，就能縮短整個工程的完成時間。如：a1、a4。
③處于所有關鍵路徑上的活動完成時間不能縮短太多，否則會使原關鍵路徑變成非關鍵路徑。這時必須重新尋找關鍵路徑。如：a1由6天變成3天，就會改變關鍵路徑。

關鍵路徑算法實現：

int CriticalPath(ALGraph G)
{?? ?//因為G是有向網，輸出G的各項關鍵活動SqStack T;int i, j;?? ?ArcNode* p;int k , dut;if(!TopologicalOrder(G,T))return 0;int vl[VexNum];for (i = 0; i < VexNum; i++)vl[i] = ve[VexNum - 1];?? ??? ?//初始化頂點事件的最遲發生時間while (T.base != T.top)?? ??? ??? ?//按拓撲逆序求各頂點的vl值{for(pop(&T, &j), p = G.vertices[j].firstarc; p; p = p->nextarc){k = p->adjvex;?? ?dut = *(p->info);?? ?//dut<j, k>if(vl[k] - dut < vl[j])vl[j] = vl[k] - dut;}//for}//whilefor(j = 0; j < G.vexnum; ++j)?? ?//求ee,el和關鍵活動{for (p = G.vertices[j].firstarc; p; p = p->nextarc){int ee, el;?? ??? ?char tag;k = p->adjvex;?? ?dut = *(p->info);ee = ve[j];?? ?el = vl[k] - dut;tag = (ee == el) ? '*' : ' ';PrintCriticalActivity(G,j,k,dut,ee,el,tag);}}return 1;
}

最短路?

最短路

????典型用途：交通網絡的問題——從甲地到乙地之間是否有公路連通？在有多條通路的情況下，哪一條路最短？
?
????交通網絡用有向網來表示：頂點——表示城市，弧——表示兩個城市有路連通，弧上的權值——表示兩城市之間的距離、交通費或途中所花費的時間等。
????如何能夠使一個城市到另一個城市的運輸時間最短或運費最省？這就是一個求兩座城市間的最短路徑問題。
????問題抽象：在有向網中A點（源點）到達B點（終點）的多條路徑中，尋找一條各邊權值之和最小的路徑，即最短路徑。最短路徑與最小生成樹不同，路徑上不一定包含n個頂點，也不一定包含n - 1條邊。
???常見最短路徑問題：單源點最短路徑、所有頂點間的最短路徑
（1）如何求得單源點最短路徑？
????窮舉法：將源點到終點的所有路徑都列出來，然后在其中選最短的一條。但是，當路徑特別多時，特別麻煩；沒有規律可循。
????迪杰斯特拉（Dijkstra）算法：按路徑長度遞增次序產生各頂點的最短路徑。
路徑長度最短的最短路徑的特點：
????在此路徑上，必定只含一條弧 <v_0, v_1>，且其權值最小。由此，只要在所有從源點出發的弧中查找權值最小者。
下一條路徑長度次短的最短路徑的特點：
①、直接從源點到v_2<v_0, v_2>（只含一條弧）；
②、從源點經過頂點v_1，再到達v_2<v_0, v_1>,<v_1, v_2>（由兩條弧組成）
再下一條路徑長度次短的最短路徑的特點：
????有以下四種情況：
????①、直接從源點到v_3<v_0, v_3>（由一條弧組成）；
????②、從源點經過頂點v_1，再到達v_3<v_0, v_1>,<v_1, v_3>（由兩條弧組成）；
????③、從源點經過頂點v_2，再到達v_3<v_0, v_2>,<v_2, v_3>（由兩條弧組成）；
????④、從源點經過頂點v_1 ?,v_2，再到達v_3<v_0, v_1>,<v_1, v_2>,<v_2, v_3>（由三條弧組成）；
其余最短路徑的特點:????
????①、直接從源點到v_i<v_0, v_i>（只含一條弧）；
????②、從源點經過已求得的最短路徑上的頂點，再到達v_i（含有多條弧）。
Dijkstra算法步驟：
????初始時令S={v_0}, ?T={其余頂點}。T中頂點對應的距離值用輔助數組D存放。
????D[i]初值：若<v_0, v_i>存在，則為其權值；否則為∞。?
????從T中選取一個其距離值最小的頂點v_j，加入S。對T中頂點的距離值進行修改：若加進v_j作中間頂點，從v_0到v_i的距離值比不加 vj 的路徑要短，則修改此距離值。
????重復上述步驟，直到 S = V 為止。

算法實現：

void ShortestPath_DIJ(MGraph G,int v0,PathMatrix &P,ShortPathTable &D)
{ // 用Dijkstra算法求有向網 G 的 v0 頂點到其余頂點v的最短路徑P[v]及帶權長度D[v]。// 若P[v][w]為TRUE,則 w 是從 v0 到 v 當前求得最短路徑上的頂點。 ?P是存放最短路徑的矩陣，經過頂點變成TRUE// final[v]為TRUE當且僅當 v∈S,即已經求得從v0到v的最短路徑。int v,w,i,j,min;Status final[MAX_VERTEX_NUM];for(v = 0 ;v < G.vexnum ;++v){final[v] = FALSE;D[v] = G.arcs[v0][v].adj;?? ??? ?//將頂點數組中下標對應是 v0 和 v的距離給了D[v]for(w = 0;w < G.vexnum; ++w)P[v][w] = FALSE;?? ??? ??? ?//設空路徑if(D[v] < INFINITY){P[v][v0] = TRUE;P[v][v] = TRUE;}}D[v0]=0;final[v0]= TRUE; /* 初始化,v0頂點屬于S集 */for(i = 1;i < G.vexnum; ++i) /* 其余G.vexnum-1個頂點 */{ /* 開始主循環,每次求得v0到某個v頂點的最短路徑,并加v到S集 */min = INFINITY; /* 當前所知離v0頂點的最近距離 */for(w = 0;w < G.vexnum; ++w)if(!final[w]) /* w頂點在V-S中 */if(D[w] < min){v = w;min = D[w];} /* w頂點離v0頂點更近 */final[v] = TRUE; /* 離v0頂點最近的v加入S集 */for(w = 0;w < G.vexnum; ++w) /* 更新當前最短路徑及距離 */{if(!final[w] && min < INFINITY && G.arcs[v][w].adj < INFINITY && (min + G.arcs[v][w].adj < D[w])){ /* 修改D[w]和P[w],w∈V-S */D[w] = min + G.arcs[v][w].adj;for(j = 0;j < G.vexnum;++j)P[w][j] = P[v][j];P[w][w] = TRUE;}}}
}

經典二分問題

經典二分問題：給定一個?n?個元素有序的（升序）整型數組?nums 和一個目標值?target? 。

寫一個函數搜索?nums?中的 target，如果目標值存在返回下標，否則返回 -1。
示例 1:

輸入: nums = [-1,0,3,5,9,12], target = 9。輸出: 4
解釋: 9 出現在 nums 中并且下標為 4
示例?2:

輸入: nums = [-1,0,3,5,9,12], target = 2。輸出: -1
解釋: 2 不存在 nums 中因此返回 -1

思路1：我們當然可以一個數一個數的遍歷，但是毫無疑問要被大媽鄙視，這可怎么辦呢？

思路2：二分查找
二分查找是一種基于比較目標值和數組中間元素的教科書式算法。

如果目標值等于中間元素，則找到目標值。
如果目標值較小，證明目標值小于中間元素及右邊的元素，繼續在左側搜索。
如果目標值較大，證明目標值大于中間元素及左邊的元素，繼續在右側搜索。

算法代碼描述：

初始化指針 left = 0, right = n - 1。
當 left <= right：
比較中間元素 nums[pivot] 和目標值 target 。
如果 target = nums[pivot]，返回 pivot。
如果 target < nums[pivot]，則在左側繼續搜索 right = pivot - 1。
如果 target > nums[pivot]，則在右側繼續搜索 left = pivot + 1。

算法實現：照例貼出三種語言的實現，在Java實現中給出了詳細注釋

class Solution {public int search(int[] nums, int target) {//分別準備好左右端點int left = 0, right = nums.length - 1;//循環二分while (left <= right) {//取中點int pivot = left + (right - left) / 2;//找到答案并返回if (nums[pivot] == target) return pivot;//向左繼續找if (target < nums[pivot]) right = pivot - 1;//向右繼續找else left = pivot + 1;}//未找到，返回-1return -1;}
}

class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1while left <= right:pivot = left + (right - left) // 2if nums[pivot] == target:return pivotif target < nums[pivot]:right = pivot - 1else:left = pivot + 1return -1

class Solution {public:int search(vector<int>& nums, int target) {int pivot, left = 0, right = nums.size() - 1;while (left <= right) {pivot = left + (right - left) / 2;if (nums[pivot] == target) return pivot;if (target < nums[pivot]) right = pivot - 1;else left = pivot + 1;}return -1;}
};

?

二叉搜索樹實現

本文給出二叉搜索樹介紹和實現

首先說它的性質：所有的節點都滿足，左子樹上所有的節點都比自己小，右邊的都比自己大。

那這個結構有什么有用呢？

首先可以快速二分查找。還可以中序遍歷得到升序序列，等等。。。

基本操作：

1、插入某個數值

2、查詢是否包含某個數值

3、刪除某個數值

根據實現不同，還可以實現其他很多種操作。

實現思路思路：

前兩個操作很好想，就是不斷比較，大了往左走，小了往右走。到空了插入，或者到空都沒找到。

而刪除稍微復雜一些，有下面這幾種情況：

1、需要刪除的節點沒有左兒子，那就把右兒子提上去就好了。

2、需要刪除的節點有左兒子，這個左兒子沒有右兒子，那么就把左兒子提上去

3、以上都不滿足，就把左兒子子孫中最大節點提上來。

當然，反過來也是成立的，比如右兒子子孫中最小的節點。

下面來敘述為什么可以這么做。

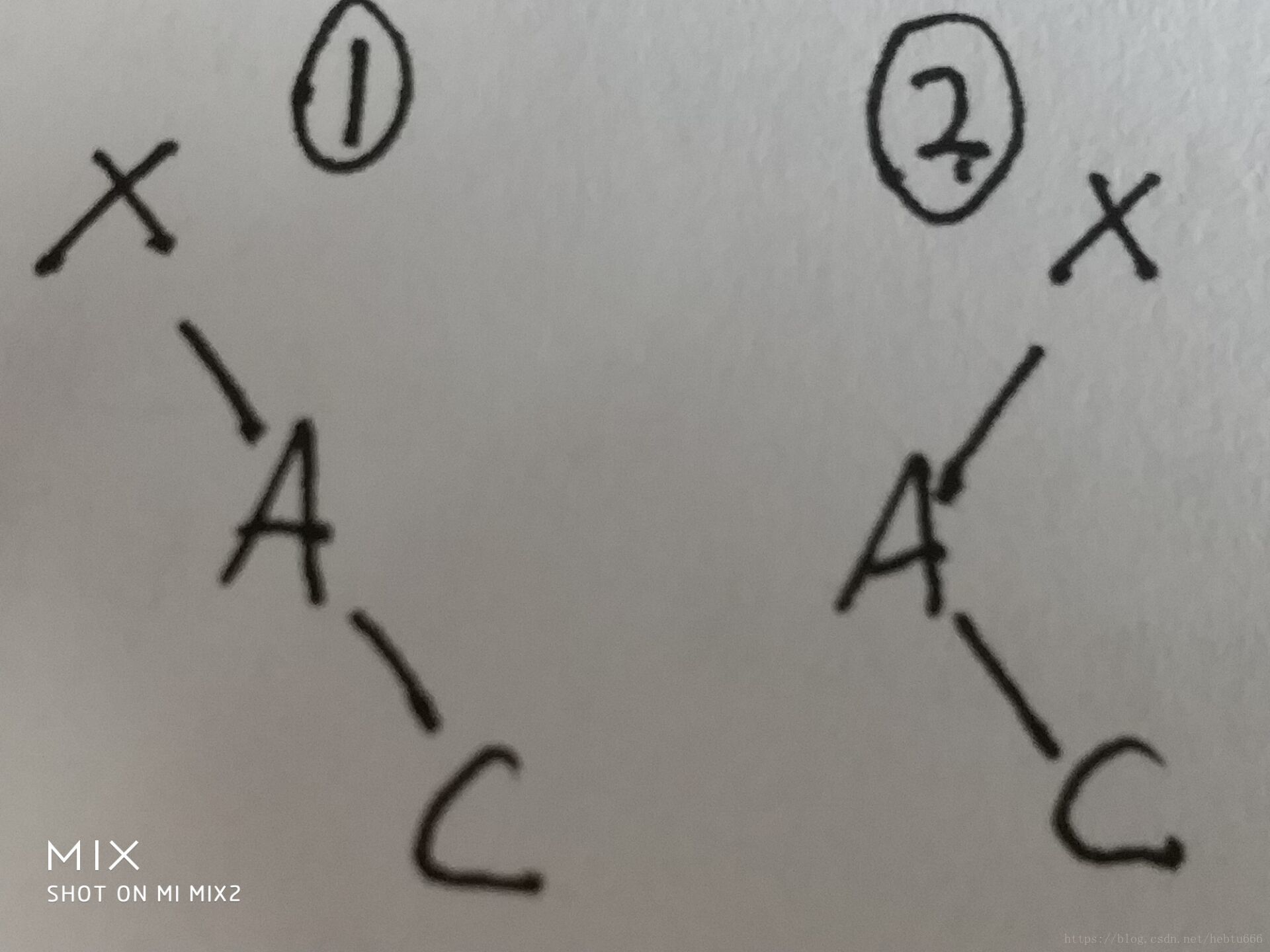
下圖中A為待刪除節點。

第一種情況：

1、去掉A，把c提上來，c也是小于x的沒問題。

2、根據定義可知，x左邊的所有點都小于它，把c提上來不影響規則。

第二種情況

3、B<A<C,所以B<C,根據剛才的敘述，B可以提上去，c可以放在b右邊，不影響規則

4、同理

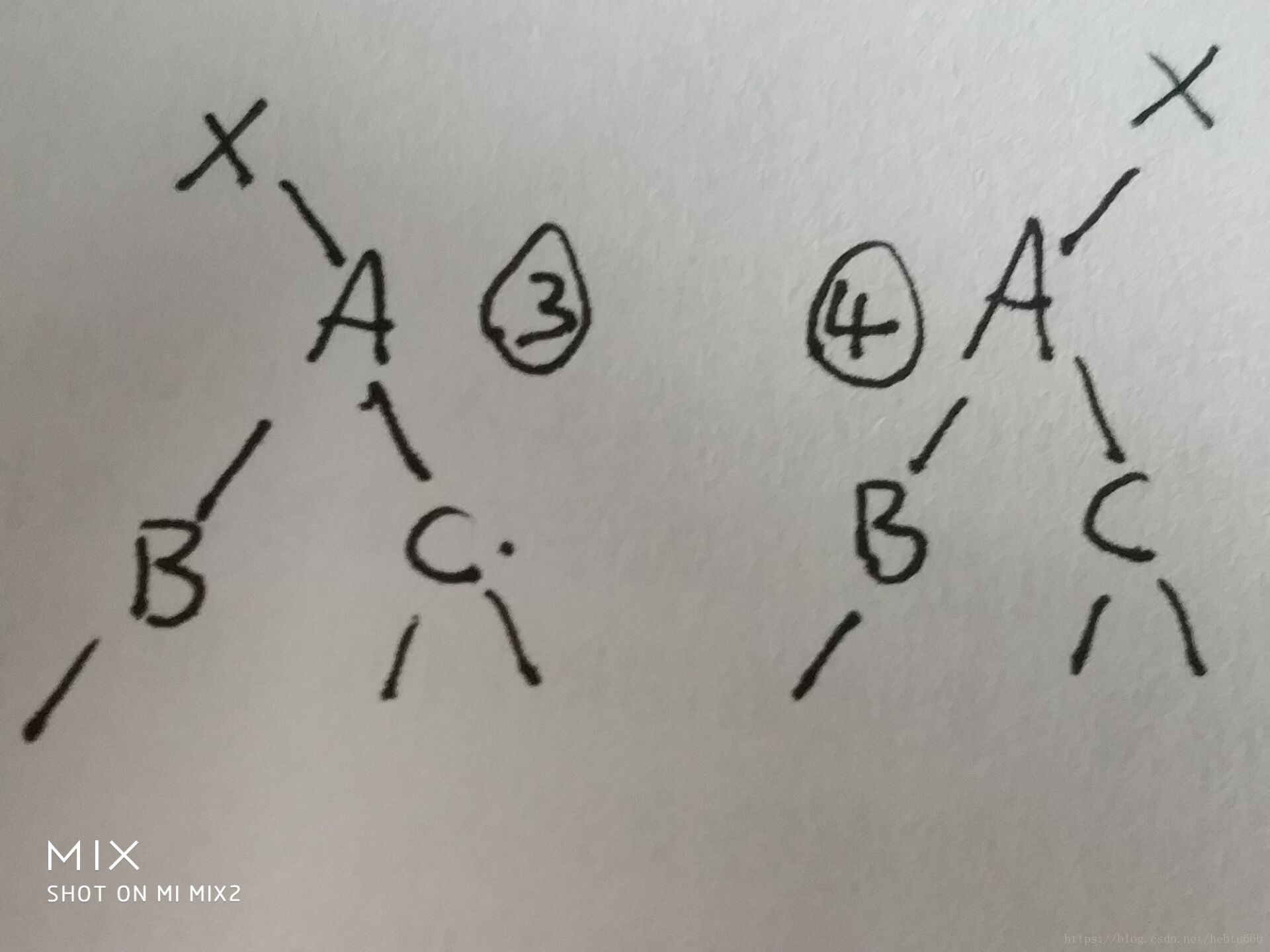
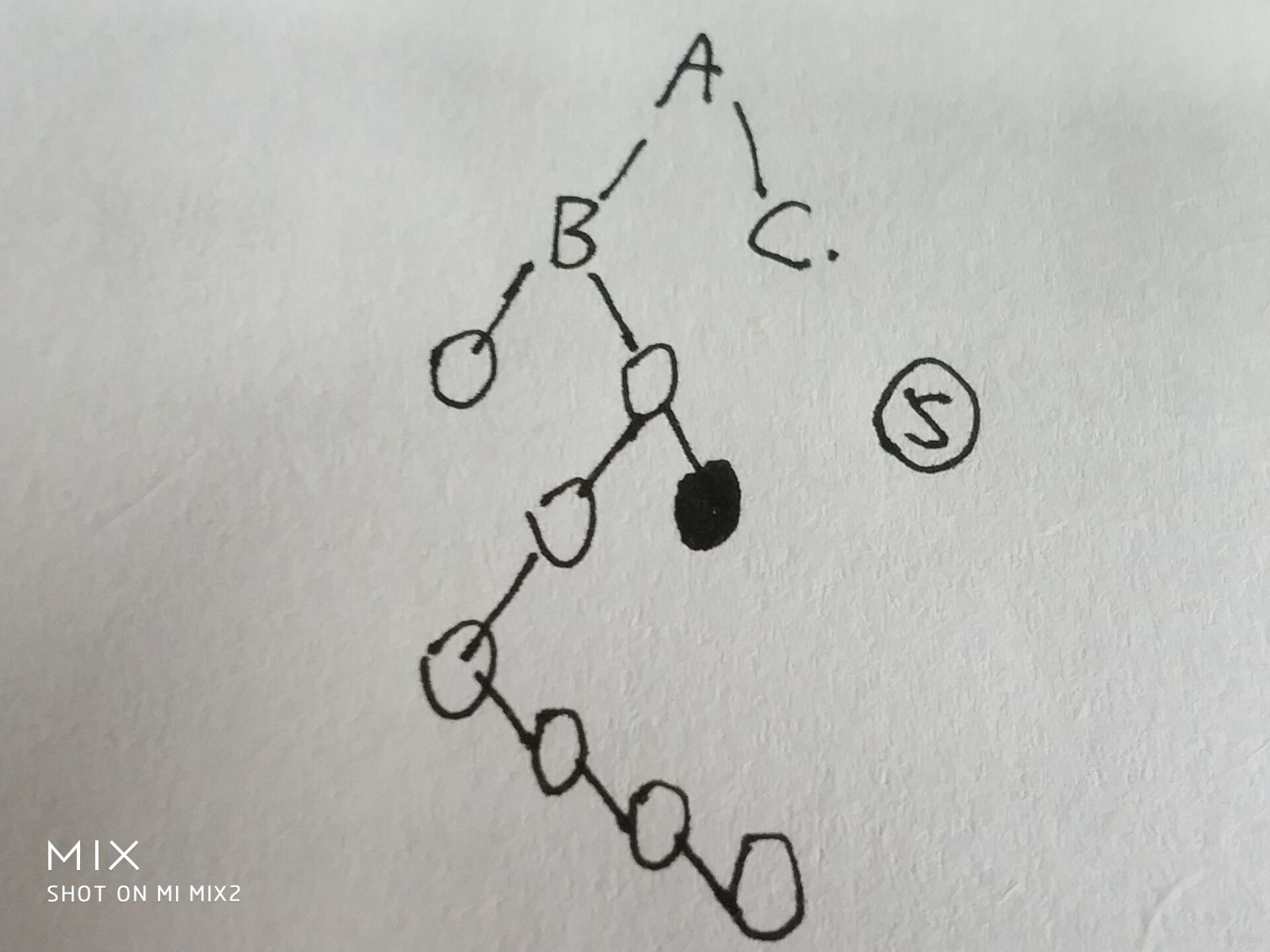
第三種情況

5、注意：是把黑色的提升上來，不是所謂的最右邊的那個，因為當初向左拐了，他一定小。

因為黑色是最大，比B以及B所有的孩子都大，所以讓B當左孩子沒問題

而黑點小于A，也就小于c，所以可以讓c當右孩子

大概證明就這樣。。

下面我們用代碼實現并通過注釋理解

上次鏈表之類的用的c，循環來寫的。這次就c++函數遞歸吧，不同方式練習。

定義

struct node
{int val;//數據node *lch,*rch;//左右孩子
};

插入

 node *insert(node *p,int x){if(p==NULL)//直到空就創建節點{node *q=new node;q->val=x;q->lch=q->rch=NULL;return p;}if(x<p->val)p->lch=insert(p->lch,x);else p->lch=insert(p->rch,x);return p;//依次返回自己，讓上一個函數執行。}

查找

 bool find(node *p,int x){if(p==NULL)return false;else if(x==p->val)return true;else if(x<p->val)return find(p->lch,x);else return find(p->rch,x);}

刪除

 node *remove(node *p,int x){if(p==NULL)return NULL;else if(x<p->val)p->lch=remove(p->lch,x);else if(x>p->val)p->lch=remove(p->rch,x);//以下為找到了之后else if(p->lch==NULL)//情況1{node *q=p->rch;delete p;return q;}else if(p->lch->rch)//情況2{node *q=p->lch;q->rch=p->rch;delete p;return q;}else{node *q;for(q=p->lch;q->rch->rch!=NULL;q=q->rch);//找到最大節點的前一個node *r=q->rch;//最大節點q->rch=r->lch;//最大節點左孩子提到最大節點位置r->lch=p->lch;//調整黑點左孩子為Br->rch=p->rch;//調整黑點右孩子為cdelete p;//刪除return r;//返回給父}return p;}

對數組排序可以說是編程基礎中的基礎，本文對八種排序方法做簡要介紹并用python實現。

代碼中注釋很全，適合復習和萌新學習。這是剛入學自己寫的，可能難免比不上標準的寫法，但是懶得改了。

文末會放和排序相關的基本拓展總結鏈接。

看不明白可以看群里視頻

注意排序實現的具體方式，不要用局部變量，否則占空間太多，和空間復雜度不符。

好，我們開始。

選擇排序

選擇排序（Selection sort）是一種簡單直觀的排序算法。它的工作原理是每一次從待排序的數據元素中選出最小（或最大）的一個元素，存放在待排序序列的起始位置，直到全部待排序的數據元素排完。時間復雜度O(N^2)

for i in range(len(l)):#意義是第i個位置開始挑第i大（小）的元素for j in range(i,len(l)):#和其他待排序的元素比較if l[j]<l[i]:#更大就交換l[j],l[i]=l[i],l[j]

冒泡排序

冒泡排序（Bubble Sort），是一種計算機科學領域的較簡單的排序算法。

它重復地走訪過要排序的元素列，一次比較兩個相鄰的元素，如果他們的順序（如從大到小、首字母從A到Z）錯誤就把他們交換過來。走訪元素的工作是重復地進行直到沒有相鄰元素需要交換(一般進行n次即可，第n次一定會把第n小的元素放到正確位置）。

這個算法的名字由來是因為越大的元素會經由交換慢慢“浮”到數列的頂端（升序或降序排列），就如同碳酸飲料中二氧化碳的氣泡最終會上浮到頂端一樣，故名“冒泡排序”。時間復雜度O(N^2)

for i in range(len(l)-1):#下標和i無關，代表的只是第i次排序，最多需要len（l）-1次排序即可for j in range(len(l)-1):#遍歷每一個元素if l[j]<l[j+1]:#本元素比下一個元素小，就交換l[j],l[j+1]=l[j+1],l[j]

?分析一下其實每次排序都會多一個元素已經確定了位置，不需要再次遍歷。

所以j循環可以改成len(l)-i-1

時間復雜度沒變。

插入排序

有一個已經有序的數據序列，要求在這個已經排好的數據序列中插入一個數，但要求插入后此數據序列仍然有序，這個時候就要用到一種新的排序方法——插入排序法,插入排序的基本操作就是將一個數據插入到已經排好序的有序數據中，從而得到一個新的、個數加一的有序數據，算法適用于少量數據的排序，時間復雜度為O(n^2)。是穩定的排序方法。

for i in range(1,len(l)):#意義是第i個元素開始插入i之前的序列（已經有序）for j in range(i,0,-1):#只要比它之前的元素小就交換if l[j]<l[j-1]:l[j],l[j-1]=l[j-1],l[j]else:break#直到比前一個元素大

歸并排序

速度僅次于快速排序，為穩定排序算法，一般用于對總體無序，但是各子項相對有序的數列

試想：假設已經有兩個有序數列，分別存放在兩個數組s，r中，我們如何把他們有序的合并在一起？

歸并排序就是在重復這樣的過程，首先單個元素合并為含有兩個元素的數組（有序），然后這種數組再和同類數組合并為四元素數組，以此類推，直到整個數組合并完畢。

def gg(l,ll):#合并函數a,b=0,0k=[]#用來合并的列表while a<len(l) and b<len(ll):#兩邊都非空if l[a]<ll[b]:k.append(l[a])a=a+1elif l[a]==ll[b]:a=a+1#實現去重else:k.append(ll[b])b=b+1k=k+l[a:]+ll[b:]#加上剩下的return kdef kk(p):#分到只剩一個元素就開始合并if len(p)<=1:return pa=kk(p[0:len(p)//2])#不止一個元素就切片b=kk(p[len(p)//2:])return gg(a,b)#返回排好序的一部分
l=list(map(int,input().split(" ")))
print(kk(l))

快速排序

快速排序（Quicksort）是對冒泡排序的一種改進。

快速排序由C. A. R. Hoare在1962年提出。它的基本思想是：通過一趟排序將要排序的數據分割成獨立的兩部分，其中一部分的所有數據都比另外一部分的所有數據都要小，然后再按此方法對這兩部分數據分別進行快速排序，整個排序過程可以遞歸進行，以此達到整個數據變成有序序列。

隨機化快排

快速排序的最壞情況基于每次劃分對主元的選擇。基本的快速排序選取第一個元素作為主元。這樣在數組已經有序的情況下，每次劃分將得到最壞的結果。比如1 2 3 4 5，每次取第一個元素，就退化為了O(N^2)。一種比較常見的優化方法是隨機化算法，即隨機選取一個元素作為主元。

這種情況下雖然最壞情況仍然是O(n^2)，但最壞情況不再依賴于輸入數據，而是由于隨機函數取值不佳。實際上，隨機化快速排序得到理論最壞情況的可能性僅為1/(2^n)。所以隨機化快速排序可以對于絕大多數輸入數據達到O(nlogn)的期望時間復雜度。

進一步提升可以分割為三部分，即小于區，等于區，大于區，減小了遞歸規模，并克服了多元素相同的退化。

def gg(a,b):global lif a>=b:#注意停止條件，我以前沒加>卡了半小時returnx,y=a,bimport random#為了避免遇到基本有序序列退化，隨機選點g=random.randint(a,b)l[g],l[y]=l[y],l[g]#交換選中元素和末尾元素while a<b:if l[a]>l[y]:#比目標元素大l[a],l[b-1]=l[b-1],l[a]#交換b=b-1#大于區擴大#注意：換過以后a不要加，因為新換過來的元素并沒有判斷過else:a=a+1#小于區擴大l[y],l[a]=l[a],l[y]#這時a=b#現在解釋a和b：a的意義是小于區下一個元素#b是大于區的第一個元素gg(x,a-1)#左右分別遞歸gg(a+1,y)l=list(map(int,input().split(" ")))
gg(0,len(l)-1)
print(l)

堆排序

堆排序（HeapSort）是一樹形選擇排序。堆排序的特點是：在排序過程中，將R[l..n]看成是一棵完全二叉樹的順序存儲結構，利用完全二叉樹中雙親結點和孩子結點之間的內在關系，在當前無序區中選擇關鍵字最大（或最小）的記錄。

由于建初始堆所需的比較次數較多，所以堆排序不適宜于記錄數較少的文件。

堆排序是就地排序，輔助空間為O(1).

它是不穩定的排序方法。

主要思想：維持一個大根堆（根結點（亦稱為堆頂）的關鍵字是堆里所有結點關鍵字中最大者，稱為大根堆，又稱最大堆。注意：①堆中任一子樹亦是堆。②以上討論的堆實際上是二叉堆（Binary Heap），類似地可定義k叉堆。）

第一步：通過調整原地建立大根堆

第二步：每次交換堆頂和邊界元素，并減枝，然后調整堆頂下沉到正確位置。

def down(i,k):#在表l里的第i元素調整，k為邊界#優先隊列也是通過這種方式實現的global lwhile 2*i+2<k:#右孩子不越界lift,right=2*i+1,2*i+2m=max(l[i],l[lift],l[right])if m==l[i]:#不需要調breakif m==l[lift]:#把最大的換上來l[i],l[lift]=l[lift],l[i]i=lift#目的節點下標更新else:#把最大的換上來l[i],l[right]=l[right],l[i]i=right#目的節點下標更新if 2*i+1<k:#判斷左孩子if l[2*i+1]>l[i]:l[i],l[2*i+1]=l[2*i+1],l[i]def main():global lfor j in range(1,len(l)+1):#調大根堆i=len(l)-jdown(i,len(l))for i in range(len(l)-1,-1,-1):#排序l[i],l[0]=l[0],l[i]#最大和邊界交換，剪枝down(0,i)print(l)l=list(map(int,input().split(" ")))
main()

桶排序

桶排序不是基于比較的排序方法，只需對號入座。將相應的數字放進相應編號的桶即可。

當要被排序的數組內的數值是均勻分配的時候，桶排序使用線性時間o（n）

對于海量有范圍數據十分適合，比如全國高考成績排序，公司年齡排序等等。

l=list(map(int,input().split(" ")))
n=max(l)-min(l)
p=[0]*(n+1)#為了省空間
for i in l:p[i-min(l)]=1#去重排序，做標記即可
for i in range(n):if p[i]==1:#判斷是否出現過print(i+min(l),end=" ")

希爾排序

希爾排序(Shell's Sort)是插入排序的一種又稱“縮小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一種更高效的改進版本。希爾排序是非穩定排序算法。該方法因D.L.Shell于1959年提出而得名。

通過縮小有序步長來實現。

def shell(arr):n=len(arr)#初始化步長h=1while h<n/3:h=3*h+1while h>=1:#判斷，退出后就有序了。for i in range(h,n):j=iwhile j>=h and arr[j]<arr[j-h]:#判斷是否交換arr[j], arr[j-h] = arr[j-h], arr[j]j-=hh=h//3#逐漸縮小步長print arr

穩定性及時間復雜度

排序穩定性概念：假定在待排序的記錄序列中，存在多個具有相同的關鍵字的記錄，若經過排序，這些記錄的相對次序保持不變，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，則稱這種排序算法是穩定的；否則稱為不穩定的。

時間復雜度：時間復雜度是同一問題可用不同算法解決，而一個算法的質量優劣將影響到算法乃至程序的效率。算法分析的目的在于選擇合適算法和改進算法。可以理解為和常數操作所成的一種關系（常數操作為O(1))

空間復雜度類似。

下面給出各類排序的對比圖：