?作為一只超級硬核的兔子，從來不給你說廢話，只有最有用的干貨！這些神級算法送給你

第一節

1.1bogo排序

1.2位運算

1.3打擂臺

1.4morris遍歷

第二節

2.1睡眠排序

2.2會死的兔子

2.3矩陣快速冪

2.4摔手機/摔雞蛋

時空復雜度目錄

二分

嘗試較優的策略

歸納表達式

寫出暴力遞歸

改為動態規劃

壓縮空間

四邊形不等式優化

換一種思路

最優解

測試：

第三節

3.1斐波那契之美

3.2桶排序

3.3快速排序

3.4BFPRT

第四節

4.1防止新手錯誤的神級代碼

4.2不用額外空間交換兩個變量

4.3八皇后問題神操作

4.4馬拉車——字符串神級算法

4.4一、分析枚舉的效率

4.4二、初步優化

4.4三、Manacher原理

假設遍歷到位置i，如何操作呢

4.4四、代碼及復雜度分析

第一節

1.1bogo排序

Bogo排序(Bogo-sort)，又被稱為猴子排序，是一種惡搞排序算法。

將元素隨機打亂，然后檢查其是否符合排列順序，若否，則繼續進行隨機打亂，繼續檢查結果，直到符合排列順序。
Bogo排序的最壞時間復雜度為O(∞)，一輩子也不能輸出排序結果，平均時間復雜度為O(n·n!)。

這讓我想到了另一個理論：猴子理論，只要讓一只猴子一直敲打計算機，理論上會有一天，它能敲出一本圣經出來，但是這個概率小到宇宙毀滅也很難敲出來。。

真的不知道這個排序應該叫做天才還是垃圾哈哈哈，但是閑的沒事的我就把他實現出來了。

public class Main {public static void main(String[] args) {int[] arr = { 9,8,7,6,5,4,3,2,1};System.out.println("排序次數" + bogo(arr));for (int i : arr) {System.out.print(i + " ");}}public static int bogo(int[] arr) {int count = 0;while (!isOrdered(arr)) {shuffle(arr);count++;}return count;}// 判斷是否有序方法public static boolean isOrdered(int[] arr) {for (int i = 1; i < arr.length; i++) {if (arr[i - 1] > arr[i]) {return false;}}return true;}// 隨機排序方法public static void shuffle(int[] arr) {int temp;for (int i = 0; i < arr.length; i++) {int j = (int) (Math.random() * arr.length);temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}}

9是中國最大的數字嘛，我就把數組長度設為9，結果平均排序次數要60萬次，不知道我的運氣怎么樣哈哈，你們也試試吧？

然而，有個看似笑話的方法聲稱可以用O(n)實現Bogo排序，依照量子理論的平行宇宙解釋，使用量子隨機性隨機地重新排列元素，不同的可能性將在不同的宇宙中展開，總有一種可能猴子得到了正確的順序，量子計算機找到了這個宇宙后，就開始毀滅其他排序不成功的宇宙，剩下一個觀察者可以看到的正確順序的宇宙。

如果想要邁出這個看似荒誕，但令人無比興奮的"高效算法"的第一步，請先證明"平行宇宙解釋"的正確性。

1.2位運算

關于位運算有很多天秀的技巧，這里舉一個例子。

給定一個非空整數數組，除了某個元素只出現一次以外，其余每個元素均出現兩次。找出那個只出現了一次的元素。

說明：你的算法應該具有線性時間復雜度。你可以不使用額外空間來實現嗎？

示例 1:

輸入: [2,2,1]輸出: 1
示例?2:

輸入: [4,1,2,1,2]輸出: 4

思路：拿map，set，都不符合要求，那怎么辦呢？

我們知道什么數字和自己異或，都等于0.

什么數字和0異或，都等于它本身，

異或又符合交換律

所以全部異或一遍，答案就是那個出現一次的數字。

class Solution {public int singleNumber(int[] nums) {int ans = 0;for(int i :nums)ans ^= i;return ans;}
}

有沒有被秒了？

1.3打擂臺

給定一個大小為 n 的數組，找到其中的多數元素。多數元素是指在數組中出現次數大于?? n/2 ??的元素。

你可以假設數組是非空的，并且給定的數組總是存在多數元素。

把狂野般的思緒收一收，咱們來看看最優解。

class Solution {public int majorityElement(int[] nums) {int count = 0;//當前答案出現的次數Integer candidate = null;//答案for (int num : nums) {if (count == 0) candidate = num;count += (num == candidate) ? 1 : -1;}return candidate;}
}

我來解釋一下策略：記錄當前的答案candidate ，記錄count。這時，我們遍歷了一個新的數字，如果和candidate 一樣，我們就讓count+1，否則讓count-1.如果count變成了0，那candidate 就下擂臺，換新的擂主（數字）上，也就是說把candidate 更新成新的數字，count也更新成1.

最后在擂臺上的一定是答案。

肯定有人懷疑這個做法的正確性吧？我就來說一下它為啥對？

首先，我們想像一下對最終隱藏答案ans最不利的情況：每個其他數字全部都打擂這個答案ans，那ans的count最后也會剩1，不會被打下來。

正常情況呢？其他數字還會互相打擂，這些數字如此“內耗”，又怎么能斗得過最終答案ans呢？對不對？

?

1.4morris遍歷

通常，實現二叉樹的前序（preorder）、中序（inorder）、后序（postorder）遍歷有兩個常用的方法：一是遞歸(recursive)，二是使用棧實現的迭代版本(stack+iterative)。這兩種方法都是O(n)的空間復雜度（遞歸本身占用stack空間或者用戶自定義的stack），我分別給出一個例子

遞歸：

void PreorderTraversal( BinTree BT )
{if(BT==NULL)return ;printf(" %c", BT->Data);PreorderTraversal(BT->Left);PreorderTraversal(BT->Right);
}

非遞歸：

*p=root;
while(p || !st.empty())
{if(p)//非空{//visit(p);進行操作st.push(p);//入棧p = p->lchild;左} else//空{p = st.top();//取出st.pop();p = p->rchild;//右}
}

為啥這個O(n)的空間就是省不掉呢？因為我們需要空間來記錄之前的位置，好在遍歷完了可以回到父節點。所以這個空間是必須的！如下圖：

比如我們遍歷2，想遍歷4，這時候我們要保證遍歷完4以后，還能回到2，我們好去繼續遍歷5等等結點，所以必須花空間記錄。

但是，還就有這么一種算法，能實現空間O(1)的遍歷，服不服。

你們可能會問，你剛說的，必須有空間來記錄路徑，怎么又可以不用空間了呢？

這就是morris遍歷，它其實是利用了葉子節點大量的空余空間來實現的，只要把他們利用起來，我們就可以省掉額外空間啦。

我們不說先序中序后序，先說morris遍歷的原則：

1、如果沒有左孩子，繼續遍歷右子樹，比如：

這個2就沒有左孩子，這時直接遍歷右孩子即可。

2、如果有左孩子，找到左子樹最右節點。

比如上圖，6就是2的最右節點。

? ? 1）如果最右節點的右指針為空（說明第一次遇到），把它指向當前節點，當前節點向左繼續處理。

修改后：

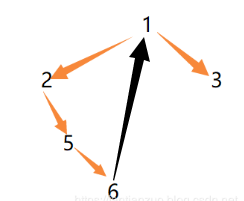
? ? 2）如果最右節點的右指針不為空（說明它指向之前結點），把右指針設為空，當前節點向右繼續處理。

這就是morris遍歷。

請手動模擬深度至少為4的樹的morris遍歷來熟悉流程。

下面給出實現：

定義結點：

	public static class Node {public int value;Node left;Node right;public Node(int data) {this.value = data;}}

先序：（完全按規則寫就好。）

//打印時機（第一次遇到）：發現左子樹最右的孩子右指針指向空，或無左子樹。public static void morrisPre(Node head) {if (head == null) {return;}Node cur1 = head;Node cur2 = null;while (cur1 != null) {cur2 = cur1.left;if (cur2 != null) {while (cur2.right != null && cur2.right != cur1) {cur2 = cur2.right;}if (cur2.right == null) {cur2.right = cur1;System.out.print(cur1.value + " ");cur1 = cur1.left;continue;} else {cur2.right = null;}} else {System.out.print(cur1.value + " ");}cur1 = cur1.right;}System.out.println();}

morris在發表文章時只寫出了中序遍歷。而先序遍歷只是打印時機不同而已，所以后人改進出了先序遍歷。至于后序，是通過打印所有的右邊界來實現的：對每個有邊界逆序，打印，再逆序回去。注意要原地逆序，否則我們morris遍歷的意義也就沒有了。

完整代碼：?

public class MorrisTraversal {public static void process(Node head) {if(head == null) {return;}// 1//System.out.println(head.value);process(head.left);// 2//System.out.println(head.value);process(head.right);// 3//System.out.println(head.value);}public static class Node {public int value;Node left;Node right;public Node(int data) {this.value = data;}}//打印時機：向右走之前public static void morrisIn(Node head) {if (head == null) {return;}Node cur1 = head;//當前節點Node cur2 = null;//最右while (cur1 != null) {cur2 = cur1.left;//左孩子不為空if (cur2 != null) {while (cur2.right != null && cur2.right != cur1) {cur2 = cur2.right;}//找到最右//右指針為空，指向cur1，cur1向左繼續if (cur2.right == null) {cur2.right = cur1;cur1 = cur1.left;continue;} else {cur2.right = null;}//右指針不為空，設為空}System.out.print(cur1.value + " ");cur1 = cur1.right;}System.out.println();}//打印時機（第一次遇到）：發現左子樹最右的孩子右指針指向空，或無左子樹。public static void morrisPre(Node head) {if (head == null) {return;}Node cur1 = head;Node cur2 = null;while (cur1 != null) {cur2 = cur1.left;if (cur2 != null) {while (cur2.right != null && cur2.right != cur1) {cur2 = cur2.right;}if (cur2.right == null) {cur2.right = cur1;System.out.print(cur1.value + " ");cur1 = cur1.left;continue;} else {cur2.right = null;}} else {System.out.print(cur1.value + " ");}cur1 = cur1.right;}System.out.println();}//逆序打印所有右邊界public static void morrisPos(Node head) {if (head == null) {return;}Node cur1 = head;Node cur2 = null;while (cur1 != null) {cur2 = cur1.left;if (cur2 != null) {while (cur2.right != null && cur2.right != cur1) {cur2 = cur2.right;}if (cur2.right == null) {cur2.right = cur1;cur1 = cur1.left;continue;} else {cur2.right = null;printEdge(cur1.left);}}cur1 = cur1.right;}printEdge(head);System.out.println();}
//逆序打印public static void printEdge(Node head) {Node tail = reverseEdge(head);Node cur = tail;while (cur != null) {System.out.print(cur.value + " ");cur = cur.right;}reverseEdge(tail);}
//逆序（類似鏈表逆序）public static Node reverseEdge(Node from) {Node pre = null;Node next = null;while (from != null) {next = from.right;from.right = pre;pre = from;from = next;}return pre;}public static void main(String[] args) {Node head = new Node(4);head.left = new Node(2);head.right = new Node(6);head.left.left = new Node(1);head.left.right = new Node(3);head.right.left = new Node(5);head.right.right = new Node(7);morrisIn(head);morrisPre(head);morrisPos(head);}}

第二節

2.1睡眠排序

這是那個員工寫的睡眠排序，寫完就被開除了哈哈哈哈。

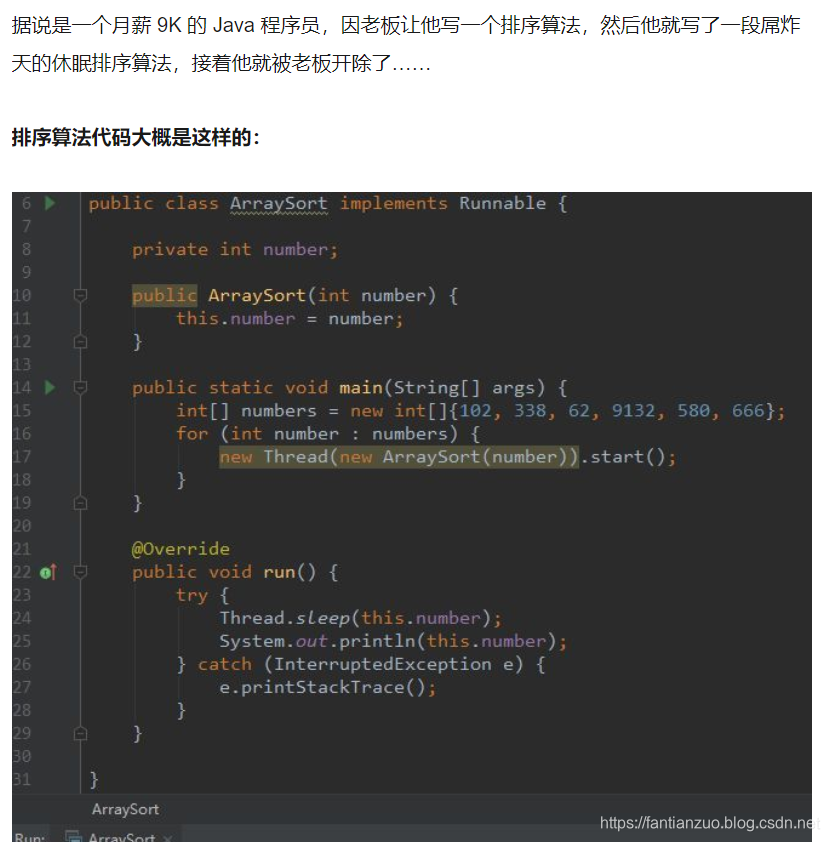
它的基本思想是：

主要是根據CPU的調度算法實現的，對一組數據進行排序，不能存在負數值，這個數是多大，那么就在線程里睡眠它的10倍再加10，不是睡眠和它的數值一樣大的原因是，當數值太小時，誤差太大，睡眠的時間不比輸出的時間少，那么就會存在不正確的輸出結果。

按道理，他的程序也沒問題啊，老板為什么要開除他？應用程序中出 BUG 不是很正常的事嗎？但他這種排序思維，能寫出這樣的隱藏 BUG 也是絕了，創造性的發明了 "休眠排序" 算法，系統里面還不知道有多少這樣的坑，不開除他開除誰啊？

如果非要說一個原因，我感覺，這哥們是故意這么寫的，造成查詢速度較慢，之后下個迭代優化，查詢速度瞬間提上來了，這可是為公司做出大貢獻了，年底了，獎勵個優秀個人獎.....

2.2會死的兔子

斐波那契數列（Fibonacci sequence），又稱黃金分割數列、因數學家列昂納多·斐波那契（Leonardoda Fibonacci）以兔子繁殖為例子而引入，故又稱為“兔子數列”。

這個例子是：剛開始，有一只兔子，這只兔子長到兩歲的時候可以生一只小兔子，以后每年都可以生一只小兔子，而且兔子不會死。求第n年有幾只兔子？

我們這么想：

今年的總數=去年的總數+今年的新出生的兔子，

而今年新出生的兔子=今年成熟了的兔子數量（每只成熟的兔子生一只小兔），

那今年成熟了的兔子數量又是什么呢？其實就是前年的兔子總數，因為前年的兔子，不管幾歲，到今年一定成熟，可以生新兔子了。而去年的沒有成熟，不能生兔子。

所以今年的總數=去年的總數+前年的總數。

F(n)=F(n-1)+F(n-2)。

這個數列就是1、1、2、3、5、8、13、21、34、……

在數學上，斐波那契數列以如下被以遞推的方法定義：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）在現代物理、準晶體結構、化學等領域，斐波納契數列都有直接的應用，為此，美國數學會從1963年起出版了以《斐波納契數列季刊》為名的一份數學雜志，用于專門刊載這方面的研究成果。

解題也非常容易

解法一：完全抄定義

def f(n):if n==1 or n==2:return 1return f(n-1)+f(n-2)

分析一下，為什么說遞歸效率很低呢？咱們來試著運行一下就知道了：

比如想求f(10)，計算機里怎么運行的？

想算出f(10)，就要先算出F(9),

想算出f(9)，就要先算出F(8),

想算出f(8)，就要先算出F(7),

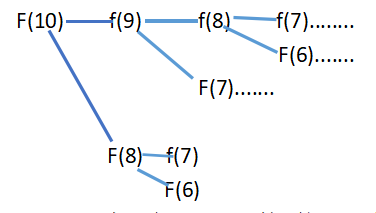
想算出f(7)，就要先算出F(6)……

兜了一圈，我們發現，有相當多的計算都重復了，比如紅框部分：

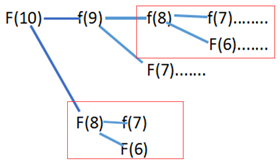
那如何解決這個問題呢？問題的原因就在于，我們算出來某個結果，并沒有記錄下來，導致了重復計算。那很容易想到如果我們把計算的結果全都保存下來，按照一定的順序推出n項，就可以提升效率

解法2：

def f1(n):if n==1 or n==2:return 1l=[0]*n??????????????? #保存結果l[0],l[1]=1,1??????????? #賦初值for i in range(2,n):l[i]=l[i-1]+l[i-2]???? #直接利用之前結果return l[-1]

可以看出，時間o(n)，空間o(n)。

繼續思考，既然只求第n項，而斐波那契又嚴格依賴前兩項，那我們何必記錄那么多值浪費空間呢？只記錄前兩項就可以了。

解法3：

def f2(n):a,b=1,1for i in range(n-1):a,b=b,a+breturn a

但是就有這么一個問題：兔子也會死

出生到死亡只有三年，即n年出生，n+3年死去。

出生一年以后可以生育，也就是n+1年開始生育，一年可以生一只寶寶。

如果你硬要推今年的總數，你會發現相當困難。

這時我們換一個思路：

定義f(n)為第n年新出生的動物個數，則f(n)=f(n-1)+f(n-2),前兩項為1，而每年的總數也就是三項求和而已。

每年出生的數量為1，1，2，3，5，8，13，21

每年總數就是1，2，4，10，16，26，42

發現依舊是前兩項加起來。

所以當我們按老思路解不出新的變形題，這時不妨換個思路，可能會有奇效，你想到了嗎？

2.3矩陣快速冪

還是上面的斐波那契數列問題（兔子不會死），這種遞推的題，一般無法突破O(N)時間的魔咒，但是我們可以利用矩陣快速冪的方法寫出O(logN)的方法，是不是很神奇？

	public static int[][] matrixPower(int[][] m, int p) {int[][] res = new int[m.length][m[0].length];for (int i = 0; i < res.length; i++) {res[i][i] = 1;}int[][] tmp = m;for (; p != 0; p >>= 1) {if ((p & 1) != 0) {res = muliMatrix(res, tmp);}tmp = muliMatrix(tmp, tmp);}return res;}public static int[][] muliMatrix(int[][] m1, int[][] m2) {int[][] res = new int[m1.length][m2[0].length];for (int i = 0; i < m1.length; i++) {for (int j = 0; j < m2[0].length; j++) {for (int k = 0; k < m2.length; k++) {res[i][j] += m1[i][k] * m2[k][j];}}}return res;}

	public static int f3(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2) {return 1;}int[][] base = { { 1, 1 }, { 1, 0 } };int[][] res = matrixPower(base, n - 2);return res[0][0] + res[1][0];}

值得思考的是，當我們一項一項的一維計算到達維度極限時，提高一個維度的計算就突破了時間極限，那么是否有三維的計算的解法？

2.4摔手機/摔雞蛋

如果對算法感興趣的朋友，可能會知道下面這道題：

leetcode的hard難度（我認為應該出一個頂級難度）：

你將獲得?K?個雞蛋，并可以使用一棟從?1?到?N??共有 N?層樓的建筑。

每個蛋的功能都是一樣的，如果一個蛋碎了，你就不能再把它掉下去。

你知道存在樓層?F ，滿足?0 <= F <= N 任何從高于 F?的樓層落下的雞蛋都會碎，從?F?樓層或比它低的樓層落下的雞蛋都不會破。

每次移動，你可以取一個雞蛋（如果你有完整的雞蛋）并把它從任一樓層?X?扔下（滿足?1 <= X <= N）。

你的目標是確切地知道 F 的值是多少。

無論 F 的初始值如何，你確定 F 的值的最小移動次數是多少？

示例 1：

輸入：K = 1, N = 2
輸出：2
解釋：雞蛋從 1 樓掉落。如果它碎了，我們肯定知道 F = 0 。
否則，雞蛋從 2 樓掉落。如果它碎了，我們肯定知道 F = 1 。
如果它沒碎，那么我們肯定知道 F = 2 。
因此，在最壞的情況下我們需要移動 2 次以確定 F 是多少。

藍橋杯：

??x星球的居民脾氣不太好，但好在他們生氣的時候唯一的異常舉動是：摔手機。
各大廠商也就紛紛推出各種耐摔型手機。x星球的質監局規定了手機必須經過耐摔測試，并且評定出一個耐摔指數來，之后才允許上市流通。
????????x星球有很多高聳入云的高塔，剛好可以用來做耐摔測試。塔的每一層高度都是一樣的，與地球上稍有不同的是，他們的第一層不是地面，而是相當于我們的2樓。
????????如果手機從第7層扔下去沒摔壞，但第8層摔壞了，則手機耐摔指數=7。

特別地，如果手機從第1層扔下去就壞了，則耐摔指數=0。如果到了塔的最高層第n層扔沒摔壞，則耐摔指數=n

????????為了減少測試次數，從每個廠家抽樣3部手機參加測試。
????????某次測試的塔高為1000層，如果我們總是采用最佳策略，在最壞的運氣下最多需要測試多少次才能確定手機的耐摔指數呢？
????????請填寫這個最多測試次數。

????????注意：需要填寫的是一個整數，不要填寫任何多余內容

答案19
問法不同，但是實際上是一個問題。

讀完題后，我們追求的不是要寫出得數（至少對于本博客是不夠的），而是用代碼實現方法，并思考是否可以優化。

其實本題的方法是非常多種多樣的。非常適合鍛煉思維。

我們把問題擴展到n個手機來思考。

手機k個，樓n層，最終結果M次。

時空復雜度目錄

暴力：? ? ? ? ? ? ? ? ? ? ? ? O(N!)

DP:? ? ? ? ? ? ? ? ? ? ? ? ? ? O(N*N*K)? O(N*K)

壓空間：? ? ? ? ? ? ? ? ? ? O(N*N*K)? O(N)

四邊形不等式優化? ? ?O(N*N)? ? ? ?

換思路：? ? ? ? ? ? ? ? ? ? O(K*M)

最優：? ? ? ? ? ? ? ? ? ? ? ? ?O(K*M)? ? O(N)

文末有測試，大家可以去直觀感受一下各方法運行的效率

二分

容易想到二分思路：不斷二分范圍，取中點，測驗是否會摔壞，然后縮小一半范圍，繼續嘗試，很顯然，答案為logN（2為底）

但是，二分得出的答案是不對的。注意:我們要保證在都手機摔完之前，能確定耐摔指數到底是多少。

舉例：

我們在500樓摔壞了，在250樓摔，又壞了。接下來，我們只能從1樓開始一層一層試

因為如果我們在125層摔壞了，就沒有手機可以用，也就是永遠都測不出來，而這是不被允許的。其實我們連測第2層都不敢測，因為在第2層摔壞了，我們就無法知道手機在第一層能否被摔壞。所以只有一部手機時，我們只敢從第一層開始摔。

嘗試較優的策略

既然二分是不對的，我們繼續分析：摔手機的最優策略到底是如何的。

只有一部手機時，我們只敢從第一層開始摔。

有兩部手機的時候，我們就敢隔層摔了，因為一部手機壞了，我們還有另一部來繼續試。

這時就有點意思了，我們分析情況：

情況1）假設我們第一部手機在i層摔壞了，然后最壞情況還要試多少次？這時我們還剩一部手機，所以只敢一層一層試，最壞情況要試到i-1層，共試了i次。

情況2）假設我們第一部手機在i層試了，但是沒摔壞，然后最壞情況還要試多少次？（這時發現算情況2時依舊是相似的問題，確定了可以用遞歸來解。）

最優解（最小值）是決策后兩種情況的最差情況（最大值），我們的本能感覺應該就是讓最差情況好一點，讓最好情況差一點，這樣比較接近正確答案。比如兩部手機，一百層，我們可以在50層摔，沒壞，這一次就很賺，我們沒摔壞手機還把范圍縮小了50層。如果壞了，就比較坑了，我們要從1試到50。雖然可能縮小一半，但是最壞情況次數太多，所以肯定要從某個低于五十的層開始嘗試。

（以上幾行是為了讓讀者理解決策，下面正文分析）

歸納表達式

假設我們的樓一共n層，我們的i可以取1-n任意值，有很多種可能的決策，我們的最小值設為f（n，k），n代表樓高（范圍為1-100或101-200其實都一樣），k代表手機數.

我們假設的決策是在第i樓扔

對于情況一，手機少了一部，并且我們確定了范圍，一定在第i樓以下，所以手機-1，層數為i-1，這時f（n，k）=f(i-1,k-1).+1

對于情況二，手機沒少，并且我們確定了范圍，一定在第i樓之上，所以手機數不變，而層數-i層，這時f（n，k）=f(n-i,k).+1

歸納出

f（n，k）=min（? max（f(i-1,k-1) ，f(n-i,k)?）?i取1-n任意數 ? ?）+1

簡單總結：怎么確定第一個手機在哪扔？每層都試試，哪層的最壞情況（max）最好（min），就去哪層扔。

寫出暴力遞歸

按照分析出來的表達式，我們可以寫出暴力遞歸：

	public static int solution1(int nLevel, int kChess) {if (nLevel == 0) {return 0;}//范圍縮小至0if (kChess == 1) {return nLevel;}//每層依次試int min = Integer.MAX_VALUE;//取不影響結果的數for (int i = 1; i != nLevel + 1; i++) {//嘗試所有決策，取最優min = Math.min(min,Math.max(Process1(i - 1, kChess - 1),Process1(nLevel - i, kChess)));}return min + 1;//別忘了加上本次}

改為動態規劃

具體思路如下

https://blog.csdn.net/hebtu666/article/details/79912328

	public static int solution2(int nLevel, int kChess) {if (kChess == 1) {return nLevel;}int[][] dp = new int[nLevel + 1][kChess + 1];for (int i = 1; i != dp.length; i++) {dp[i][1] = i;}for (int i = 1; i != dp.length; i++) {for (int j = 2; j != dp[0].length; j++) {int min = Integer.MAX_VALUE;for (int k = 1; k != i + 1; k++) {min = Math.min(min,Math.max(dp[k - 1][j - 1], dp[i - k][j]));}dp[i][j] = min + 1;}}return dp[nLevel][kChess];}

壓縮空間

我們發現，對于狀態轉移方程，只和上一盤排的dp表和左邊的dp表有關，所以我們不需要把值全部記錄，用兩個長度為n的數組不斷更新即可（具體對dp壓縮空間的思路，也是很重要的，我在其它文章中有提過，在這里就不寫了）

	public static int solution3(int nLevel, int kChess) {if (kChess == 1) {return nLevel;}int[] preArr = new int[nLevel + 1];int[] curArr = new int[nLevel + 1];for (int i = 1; i != curArr.length; i++) {curArr[i] = i;}//初始化for (int i = 1; i != kChess; i++) {//先交換int[] tmp = preArr;preArr = curArr;curArr = tmp;//然后打新的一行for (int j = 1; j != curArr.length; j++) {int min = Integer.MAX_VALUE;for (int k = 1; k != j + 1; k++) {min = Math.min(min, Math.max(preArr[k - 1], curArr[j - k]));}curArr[j] = min + 1;}}return curArr[curArr.length - 1];}

四邊形不等式優化

四邊形不等式是一種比較常見的優化動態規劃的方法

定義：如果對于任意的a1≤a2<b1≤b2，有m[a1,b1]+m[a2,b2]≤m[a1,b2]+m[a2,b1]，那么m[i,j]滿足四邊形不等式。

對s[i,j-1]≤s[i,j]≤s[i+1,j]的證明：

設mk[i,j]=m[i,k]+m[k,j]，s[i,j]=d

對于任意k<d，有mk[i,j]≥md[i,j]（這里以m[i,j]=min{m[i,k]+m[k,j]}為例,max的類似），接下來只要證明mk[i+1,j]≥md[i+1,j]，那么只有當s[i+1,j]≥s[i,j]時才有可能有mk[i+1,j]≥md[i+1,j]

(mk[i+1,j]-md[i+1,j])-(mk[i,j]-md[i,j])

=(mk[i+1,j]+md[i,j])-(md[i+1,j]+mk[i,j])

=(m[i+1,k]+m[k,j]+m[i,d]+m[d,j])-(m[i+1,d]+m[d,j]+m[i,k]+m[k,j])

=(m[i+1,k]+m[i,d])-(m[i+1,d]+m[i,k])

∵m滿足四邊形不等式，∴對于i<i+1≤k<d有m[i+1,k]+m[i,d]≥m[i+1,d]+m[i,k]

∴(mk[i+1,j]-md[i+1,j])≥(mk[i,j]-md[i,j])≥0

∴s[i,j]≤s[i+1,j]，同理可證s[i,j-1]≤s[i,j]

證畢

通俗來說，

優化策略1）我們在求k+1手機n層樓時，最后發現，第一個手機在m層扔導致了最優解的產生。那我們在求k個手機n層樓時，第一個手機的策略就不用嘗試m層以上的樓了。

優化策略2）我們在求k個手機n層樓時，最后發現，第一個手機在m層扔導致了最優解的產生。那我們在求k個手機n+1層樓時，就不用嘗試m層以下的樓了。

	public static int solution4(int nLevel, int kChess) {if (kChess == 1) {return nLevel;}int[][] dp = new int[nLevel + 1][kChess + 1];for (int i = 1; i != dp.length; i++) {dp[i][1] = i;}int[] cands = new int[kChess + 1];for (int i = 1; i != dp[0].length; i++) {dp[1][i] = 1;cands[i] = 1;}for (int i = 2; i < nLevel + 1; i++) {for (int j = kChess; j > 1; j--) {int min = Integer.MAX_VALUE;int minEnum = cands[j];int maxEnum = j == kChess ? i / 2 + 1 : cands[j + 1];//優化策略for (int k = minEnum; k < maxEnum + 1; k++) {int cur = Math.max(dp[k - 1][j - 1], dp[i - k][j]);if (cur <= min) {min = cur;cands[j] = k;//最優解記錄層數}}dp[i][j] = min + 1;}}return dp[nLevel][kChess];}

注：對于四邊形不等式的題目，比賽時不需要嚴格證明

通常的做法是打表出來之后找規律，然后大膽猜測，顯然可得。（手動滑稽）

換一種思路

有時，最優解并不是優化來的。

當你對著某個題冥思苦想了好久，無論如何也不知道怎么把時間優化到合理范圍，可能這個題的最優解就不是這種思路，這時，試著換一種思路思考，可能會有奇效。

（比如訓練時一道貪心我死活往dp想，肝了兩個小時以后，不主攻這個方向的隊友三分鐘就有貪心思路了，淚目，不要把簡單問題復雜化）

我們換一種思路想問題：

原問題：n層樓，k個手機，最多測試次數

反過來看問題：k個手機，扔m次，最多能確定多少層樓？

我們定義dp[i][j]：i個手機扔j次能確定的樓數。

分析情況：依舊是看第一部手機在哪層扔的決策，同樣，我們的決策首先要保證能確定從1層某一段，而不能出現次數用完了還沒確定好的情況。以這個為前提，保證了每次扔的樓層都是最優的，就能求出結果。

依舊是取最壞情況：min（情況1，情況2）

情況1）第一個手機碎了，我們就需要用剩下的i-1個手機和j-1次測試次數往下去測，dp[i-1][j-1]。那我們能確定的層數是無限的，因為本層以上的無限層樓都不會被摔壞。dp[i-1][j-1]+無窮=無窮

情況2）第一個手機沒碎，那我們就看i個手機扔j-1次能確定的樓數（向上試）+當前樓高h

歸納表達式，要取最差情況，所以就是只有情況2：dp[i][j]=dp[i-1][j-1]+h

那這個h到底是什么呢？取決于我敢從哪層扔。因為次數減了一次，我們還是要考慮i個球和j-1次的最壞情況能確定多少層，我才敢在層數+1的地方扔。（這是重點）

也就是dp[i][j-1]的向上一層：h=dp[i][j-1]+1

總：min（情況1，情況2）=min（無窮，dp[i-1][j-1]+dp[i][j-1]+1）=dp[i-1][j-1]+dp[i][j-1]+1

這是解決k個手機，扔m次，最多能確定多少層樓？

原問題是n層樓，k個手機，最多測試次數。

所以我們在求的過程中，何時能確定的層數大于n，輸出扔的次數即可

最優解

我們知道完全用二分扔需要logN+1次，這也絕對是手機足夠情況下的最優解，我們做的這么多努力都是因為手機不夠摔啊。。。。所以當我們的手機足夠用二分來摔時，直接求出logN+1即可。

當然，我們求dp需要左邊的值和左上的值：

依舊可以壓縮空間，從左往右更新，previous記錄左上的值。

求自己時也要注意記錄，否則更新過后，后面的要用沒更新過的值（左上方）就找不到了。

記錄之后，求出當前數值，把記錄的temp值給了previous即可。

	public static int solution5(int nLevel, int kChess) {int bsTimes = log2N(nLevel) + 1;if (kChess >= bsTimes) {return bsTimes;}int[] dp = new int[kChess];int res = 0;while (true) {res++;//壓縮空間記得記錄次數int previous = 0;for (int i = 0; i < dp.length; i++) {int tmp = dp[i];dp[i] = dp[i] + previous + 1;previous = tmp;if (dp[i] >= nLevel) {return res;}}}}public static int log2N(int n) {int res = -1;while (n != 0) {res++;n >>>= 1;}return res;}

測試：

暴力：? ? ? ? ? ? ? ? ? ? ? ? O(N!)

DP:? ? ? ? ? ? ? ? ? ? ? ? ? ? O(N*N*K)? O(N*K)

壓空間：? ? ? ? ? ? ? ? ? ? O(N*N*K)? O(N)

四邊形不等式優化? ? ?O(N*N)? ? ? ?

最優：? ? ? ? ? ? ? ? ? ? ? ? ?O(K*M)? ? O(N)

		long start = System.currentTimeMillis();solution1(30, 2);long end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + " ms");start = System.currentTimeMillis();solution2(30, 2);end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + " ms");start = System.currentTimeMillis();solution3(30, 2);end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + " ms");start = System.currentTimeMillis();solution4(30, 2);end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + " ms");start = System.currentTimeMillis();solution5(30, 2);end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + " ms");
/*
結果：
cost time: 7043 ms
cost time: 0 ms
cost time: 0 ms
cost time: 0 ms
cost time: 0 ms
*/

暴力時間實在是太久了，只測一個30，2

后四種方法測的大一些（差點把電腦測炸了，cpu100內存100）：

solution(100000, 10):

solution2 cost time: 202525 ms
solution3 cost time: 38131 ms
solution4 cost time: 11295 ms
solution5 cost time: 0 ms

感受最優解的強大：

solution5(1000 000 000,100):0 ms

solution5(1000 000 000,10):0 ms

最優解永遠都是0 ms，我也是服了。。

對比方法，在時間復雜度相同的條件下，空間復雜度一樣會影響時間，因為空間太大的話，申請空間是相當浪費時間的。并且空間太大電腦會炸，所以不要認為空間不重要。

第三節

3.1斐波那契之美

這個數列就是1、1、2、3、5、8、13、21、34、……

但是斐波那契的知識不止于此，它還有很多驚艷到我的地方，下面我們就一起了解一下：

隨著數列項數的增加，前一項與后一項之比越來越逼近黃金分割的數值0.6180339887..
從第二項開始，每個奇數項的平方都比前后兩項之積多1，每個偶數項的平方都比前后兩項之積少1。（注：奇數項和偶數項是指項數的奇偶，而并不是指數列的數字本身的奇偶，比如第五項的平方比前后兩項之積多1，第四項的平方比前后兩項之積少1）
斐波那契數列的第n項同時也代表了集合{1,2,…,n}中所有不包含相鄰正整數的子集個數。
f(0)+f(1)+f(2)+…+f(n)=f(n+2)-1
f(1)+f(3)+f(5)+…+f(2n-1)=f(2n)
f(2)+f(4)+f(6)+…+f(2n) =f(2n+1)-1
[f(0)]^2+[f(1)]^2+…+[f(n)]^2=f(n)·f(n+1)
f(0)-f(1)+f(2)-…+(-1)^n·f(n)=(-1)^n·[f(n+1)-f(n)]+1
f(m+n)=f(m-1)·f(n-1)+f(m)·f(n) (利用這一點，可以用程序編出時間復雜度僅為O（log n）的程序。)

真的不禁感嘆：真是一個神奇的數列啊

3.2桶排序

我們都知道，基于比較的排序，時間的極限就是O(NlogN)，從來沒有哪個排序可以突破這個界限，如速度最快的快速排序，想法新穎的堆排序，分治的歸并排序。

但是，如果我們的排序根本就不基于比較，那就可能突破這個時間。

桶排序不是基于比較的排序方法，只需對號入座。將相應的數字放進相應編號的桶即可。

當要被排序的數組內的數值是均勻分配的時候，桶排序使用線性時間o（n）

對于海量有范圍數據十分適合，比如全國高考成績排序，公司年齡排序等等。

l=list(map(int,input().split(" ")))
n=max(l)-min(l)
p=[0]*(n+1)#為了省空間
for i in l:p[i-min(l)]=1#去重排序，做標記即可
for i in range(n):if p[i]==1:#判斷是否出現過print(i+min(l),end=" ")

當然，基數排序是桶排序的改良版，也是非常好的排序方法，具體操作是：把數字的每一位都按桶排序排一次，因為桶排序是穩定的排序，因此從個位進行桶排序，然后十位進行桶排序。。。直到最高位，排序結束。

這樣極大的弱化了桶排序范圍有限的弱點，比如范圍1-100000需要準備100000個銅，而基數排序只要10個銅就夠了（因為一共就十個數字。）。

想出這個排序的人也是個天才啊。。。選擇合適的場合使用覺得有很好的效果。

3.3快速排序

快速排序（Quicksort）是對冒泡排序的一種改進。

快速排序由C. A. R. Hoare在1962年提出。它的基本思想是：通過一趟排序將要排序的數據分割成獨立的兩部分，其中一部分的所有數據都比另外一部分的所有數據都要小，然后再按此方法對這兩部分數據分別進行快速排序，整個排序過程可以遞歸進行，以此達到整個數據變成有序序列。
分三區優化1：

在使用partition-exchange排序算法時，如快速排序算法，我們會遇到一些問題，比如重復元素太多，降低了效率，在每次遞歸中，左邊部分是空的(沒有元素比關鍵元素小)，而右邊部分只能一個一個遞減移動。結果導致耗費了二次方時間來排序相等元素。這時我們可以多分一個區，即，小于區，等于區，大于區。（傳統快排為小于區和大于區）

下面我們通過一個經典例題來練習這種思想。

荷蘭國旗問題

”荷蘭國旗難題“是計算機科學中的一個程序難題，它是由Edsger Dijkstra提出的。荷蘭國旗是由紅、白、藍三色組成的。

現在有若干個紅、白、藍三種顏色的球隨機排列成一條直線。現在我們的任務是把這些球按照紅、白、藍排序。

樣例輸入

3
BBRRWBWRRR
RRRWWRWRB
RBRW
樣例輸出

RRRRRWWBBB
RRRRRWWWB
RRWB
思路：

現在我們的思路就是把未排序時前部和后部分別排在數組的前面和后面，那么中部自然就排好了。

設置兩個標志位head指向數組開頭，tail指向數組末尾，now從頭開始遍歷：

(1)如果遍歷到的位置為1，那么它一定是屬于前部，于是就和head交換值，然后head++，now++；

(2)如果遍歷到的位置為2，說明屬于中部，now++；

(3)如果遍歷到的位置為3，說明屬于后部，于是就和tail交換值，然而，如果此時交換后now指向的值屬于前部，那么就執行(1)，tail--；

廢話不多說，上代碼。

#include<iostream>
#include<algorithm>
using namespace std;const int maxn = 100 + 5;int n;
string str;
int main(){cin>>n;while(n--){cin>>str;int len=str.size();int now=0,ans=0;int head=0,tail=len-1;while(now<=tail){if(str[now]=='R'){swap(str[head],str[now]);head++;now++;}else if(str[now]=='W'){now++;}else{swap(str[now],str[tail]);tail--;}}cout<<str<<endl;}return 0;
}

快排分三區以后降低了遞歸規模，避免了最差情況，性能得到改進。
但是還是存在退化情況：

隨機化快排優化2：
快速排序的最壞情況基于每次劃分對主元的選擇。基本的快速排序選取第一個元素作為主元。這樣在數組已經有序的情況下，每次劃分將得到最壞的結果。比如1 2 3 4 5，每次取第一個元素，就退化為了O(N^2)。一種比較常見的優化方法是隨機化算法，即隨機選取一個元素作為主元。

這種情況下雖然最壞情況仍然是O(n^2)，但最壞情況不再依賴于輸入數據，而是由于隨機函數取值不佳。實際上，隨機化快速排序得到理論最壞情況的可能性僅為1/(2^n)。所以隨機化快速排序可以對于絕大多數輸入數據達到O(nlogn)的期望時間復雜度。
?

def gg(a,b):global lif a>=b:#注意停止條件，我以前沒加>卡了半小時returnx,y=a,bimport random#為了避免遇到基本有序序列退化，隨機選點g=random.randint(a,b)l[g],l[y]=l[y],l[g]#交換選中元素和末尾元素while a<b:if l[a]>l[y]:#比目標元素大l[a],l[b-1]=l[b-1],l[a]#交換b=b-1#大于區擴大#注意：換過以后a不要加，因為新換過來的元素并沒有判斷過else:a=a+1#小于區擴大l[y],l[a]=l[a],l[y]#這時a=b#現在解釋a和b：a的意義是小于區下一個元素#b是大于區的第一個元素gg(x,a-1)#左右分別遞歸gg(a+1,y)l=list(map(int,input().split(" ")))
gg(0,len(l)-1)
print(l)

3.4BFPRT

我們以前寫過快排的改進求前k大或前k小，但是快排不可避免地存在退化問題，即使我們用了隨機數等優化，最差情況不可避免的退化到了O(N^2），而BFPRT就解決了這個問題，主要的思想精華就是怎么選取劃分值。

我們知道，經典快排是選第一個數進行劃分。而改進快排是隨機選取一個數進行劃分，從概率上避免了基本有序情況的退化。而BFPRT算法選劃分值的規則比較特殊，保證了遞歸最小的縮減規模也會比較大，而不是每次縮小一個數。

這個劃分值如何劃分就是重點。

如何讓選取的點無論如何都不會太差。

1、將n個元素劃分為n/5個組，每組5個元素
2、對每組排序，找到n/5個組中每一組的中位數；?
3、對于找到的所有中位數，調用BFPRT算法求出它們的中位數，作為劃分值。

下面說明為什么這樣找劃分值。

我們先把數每五個分為一組。

同一列為一組。

排序之后，第三行就是各組的中位數。

我們把第三行的數構成一個數列，遞歸找，找到中位數。

這個黑色框為什么找的很好。

因為他一定比A3、B3大，而A3、B3、C3又在自己的組內比兩個數要大。

我們看最差情況：求算其它的數都比c3大，我們也能在25個數中縮小九個數的規模。大約3/10.

我們就做到了最差情況固定遞減規模，而不是可能縮小的很少。

下面代碼實現：

public class BFPRT {
//前k小public static int[] getMinKNumsByBFPRT(int[] arr, int k) {if (k < 1 || k > arr.length) {return arr;}int minKth = getMinKthByBFPRT(arr, k);int[] res = new int[k];int index = 0;for (int i = 0; i != arr.length; i++) {if (arr[i] < minKth) {res[index++] = arr[i];}}for (; index != res.length; index++) {res[index] = minKth;}return res;}
//第k小public static int getMinKthByBFPRT(int[] arr, int K) {int[] copyArr = copyArray(arr);return select(copyArr, 0, copyArr.length - 1, K - 1);}public static int[] copyArray(int[] arr) {int[] res = new int[arr.length];for (int i = 0; i != res.length; i++) {res[i] = arr[i];}return res;}
//給定一個數組和范圍，求第i小的數public static int select(int[] arr, int begin, int end, int i) {if (begin == end) {return arr[begin];}int pivot = medianOfMedians(arr, begin, end);//劃分值int[] pivotRange = partition(arr, begin, end, pivot);if (i >= pivotRange[0] && i <= pivotRange[1]) {return arr[i];} else if (i < pivotRange[0]) {return select(arr, begin, pivotRange[0] - 1, i);} else {return select(arr, pivotRange[1] + 1, end, i);}}
//在begin end范圍內進行操作public static int medianOfMedians(int[] arr, int begin, int end) {int num = end - begin + 1;int offset = num % 5 == 0 ? 0 : 1;//最后一組的情況int[] mArr = new int[num / 5 + offset];//中位數組成的數組for (int i = 0; i < mArr.length; i++) {int beginI = begin + i * 5;int endI = beginI + 4;mArr[i] = getMedian(arr, beginI, Math.min(end, endI));}return select(mArr, 0, mArr.length - 1, mArr.length / 2);//只不過i等于長度一半，用來求中位數}
//經典partition過程public static int[] partition(int[] arr, int begin, int end, int pivotValue) {int small = begin - 1;int cur = begin;int big = end + 1;while (cur != big) {if (arr[cur] < pivotValue) {swap(arr, ++small, cur++);} else if (arr[cur] > pivotValue) {swap(arr, cur, --big);} else {cur++;}}int[] range = new int[2];range[0] = small + 1;range[1] = big - 1;return range;}
//五個數排序，返回中位數public static int getMedian(int[] arr, int begin, int end) {insertionSort(arr, begin, end);int sum = end + begin;int mid = (sum / 2) + (sum % 2);return arr[mid];}
//手寫排序public static void insertionSort(int[] arr, int begin, int end) {for (int i = begin + 1; i != end + 1; i++) {for (int j = i; j != begin; j--) {if (arr[j - 1] > arr[j]) {swap(arr, j - 1, j);} else {break;}}}}
//交換值public static void swap(int[] arr, int index1, int index2) {int tmp = arr[index1];arr[index1] = arr[index2];arr[index2] = tmp;}
//打印public static void printArray(int[] arr) {for (int i = 0; i != arr.length; i++) {System.out.print(arr[i] + " ");}System.out.println();}public static void main(String[] args) {int[] arr = { 6, 9, 1, 3, 1, 2, 2, 5, 6, 1, 3, 5, 9, 7, 2, 5, 6, 1, 9 };// sorted : { 1, 1, 1, 1, 2, 2, 2, 3, 3, 5, 5, 5, 6, 6, 6, 7, 9, 9, 9 }printArray(getMinKNumsByBFPRT(arr, 10));}
}

這個辦法解決了最差的退化情況，在一大堆數中求其前k大或前k小的問題，簡稱TOP-K問題。目前解決TOP-K問題最有效的算法即是BFPRT算法，其又稱為中位數的中位數算法，該算法由Blum、Floyd、Pratt、Rivest、Tarjan提出?，讓我們永遠記住這群偉大的人。

第四節

4.1防止新手錯誤的神級代碼

#define ture true

#define flase false

#difine viod void

#define mian main

#define ； ;

以后有新手問題就把這幾行代碼給他就好啦。

4.2不用額外空間交換兩個變量

a?=?5
b?=?8

#計算a和b兩個點到原點的距離之和，并且賦值給a
a?=?a+b

#使用距離之和減去b到原點的距離
#a-b?其實就是a的原值（a到原點的距離），現在賦值給了b
b?=?a-b

#再使用距離之和減去b?(a到原點的距離)
#得到的是b的原值（b到原點的距離），現在賦值給了a
a?=?a-b

4.3八皇后問題神操作

是一個以國際象棋為背景的問題：如何能夠在 8×8 的國際象棋棋盤上放置八個皇后，使得任何一個皇后都無法直接吃掉其他的皇后？為了達到此目的，任兩個皇后都不能處于同一條橫行、縱行或斜線上。八皇后問題可以推廣為更一般的n皇后擺放問題：這時棋盤的大小變為n1×n1，而皇后個數也變成n2。而且僅當 n2 ≥ 1 或 n1 ≥ 4 時問題有解。

皇后問題是非常著名的問題，作為一個棋盤類問題，毫無疑問，用暴力搜索的方法來做是一定可以得到正確答案的，但在有限的運行時間內，我們很難寫出速度可以忍受的搜索，部分棋盤問題的最優解不是搜索，而是動態規劃，某些棋盤問題也很適合作為狀態壓縮思想的解釋例題。

進一步說，皇后問題可以用人工智能相關算法和遺傳算法求解，可以用多線程技術縮短運行時間。本文不做討論。

（本文不展開講狀態壓縮，以后再說）

一般思路：

N*N的二維數組，在每一個位置進行嘗試，在當前位置上判斷是否滿足放置皇后的條件（這一點的行、列、對角線上，沒有皇后）。

優化1：

既然知道多個皇后不能在同一行，我們何必要在同一行的不同位置放多個來嘗試呢？

我們生成一維數組record，record[i]表示第i行的皇后放在了第幾列。對于每一行，確定當前record值即可，因為每行只能且必須放一個皇后，放了一個就無需繼續嘗試。那么對于當前的record[i]，查看record[0...i-1]的值，是否有j = record[k]（同列）、|record[k] - j| = | k-i |（同一斜線）的情況。由于我們的策略，無需檢查行（每行只放一個）。

public class NQueens {public static int num1(int n) {if (n < 1) {return 0;}int[] record = new int[n];return process1(0, record, n);}public static int process1(int i, int[] record, int n) {if (i == n) {return 1;}int res = 0;for (int j = 0; j < n; j++) {if (isValid(record, i, j)) {record[i] = j;res += process1(i + 1, record, n);}}//對于當前行，依次嘗試每列return res;}
//判斷當前位置是否可以放置public static boolean isValid(int[] record, int i, int j) {for (int k = 0; k < i; k++) {if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {return false;}}return true;}public static void main(String[] args) {int n = 8;System.out.println(num1(n));}
}

位運算優化2：

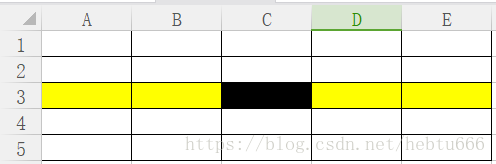
分析：棋子對后續過程的影響范圍：本行、本列、左右斜線。

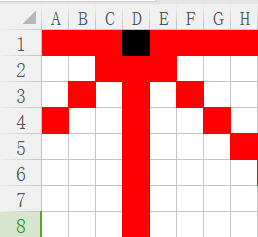
黑色棋子影響區域為紅色

1）本行影響不提，根據優化一已經避免

2）本列影響，一直影響D列，直到第一行在D放棋子的所有情況結束。

3）左斜線：每向下一行，實際上對當前行的影響區域就向左移動

比如：

嘗試第二行時，黑色棋子影響的是我們的第三列；

嘗試第三行時，黑色棋子影響的是我們的第二列；

嘗試第四行時，黑色棋子影響的是我們的第一列；

嘗試第五行及以后幾行，黑色棋子對我們并無影響。

4）右斜線則相反：

隨著行序號增加，影響的列序號也增加，直到影響的列序號大于8就不再影響。

我們對于之前棋子影響的區域，可以用二進制數字來表示，比如:

每一位，用01代表是否影響。

比如上圖，對于第一行，就是00010000

嘗試第二行時，數字變為00100000

第三行：01000000

第四行：10000000

對于右斜線的數字，同理：

第一行00010000，之后向右移：00001000，00000100，00000010，00000001，直到全0不影響。

同理，我們對于多行數據，也同樣可以記錄了

比如在第一行我們放在了第四列：

第二行放在了G列，這時左斜線記錄為00100000（第一個棋子的影響）+00000010（當前棋子的影響）=00100010。

到第三行數字繼續左移：01000100，然后繼續加上我們的選擇，如此反復。

這樣，我們對于當前位置的判斷，其實可以通過左斜線變量、右斜線變量、列變量，按位或運算求出（每一位中，三個數有一個是1就不能再放）。

具體看代碼：

注：怎么排版就炸了呢。。。貼一張圖吧

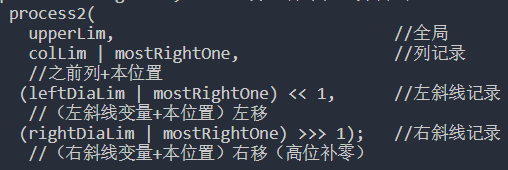
public class NQueens {public static int num2(int n) {// 因為本方法中位運算的載體是int型變量，所以該方法只能算1~32皇后問題// 如果想計算更多的皇后問題，需使用包含更多位的變量if (n < 1 || n > 32) {return 0;}int upperLim = n == 32 ? -1 : (1 << n) - 1;//upperLim的作用為棋盤大小，比如8皇后為00000000 00000000 00000000 11111111//32皇后為11111111 11111111 11111111 11111111return process2(upperLim, 0, 0, 0);}public static int process2(int upperLim, int colLim, int leftDiaLim,int rightDiaLim) {if (colLim == upperLim) {return 1;}int pos = 0;            //pos：所有的合法位置int mostRightOne = 0;   //所有合法位置的最右位置//所有記錄按位或之后取反，并與全1按位與，得出所有合法位置pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));int res = 0;//計數while (pos != 0) {mostRightOne = pos & (~pos + 1);//取最右的合法位置pos = pos - mostRightOne;       //去掉本位置并嘗試res += process2(upperLim,                             //全局colLim | mostRightOne,                //列記錄//之前列+本位置(leftDiaLim | mostRightOne) << 1,      //左斜線記錄//（左斜線變量+本位置）左移             (rightDiaLim | mostRightOne) >>> 1);   //右斜線記錄//（右斜線變量+本位置）右移（高位補零）}return res;}public static void main(String[] args) {int n = 8;System.out.println(num2(n));}
}

完整測試代碼：

32皇后：結果/時間

暴力搜：時間就太長了，懶得測。。。

public class NQueens {public static int num1(int n) {if (n < 1) {return 0;}int[] record = new int[n];return process1(0, record, n);}public static int process1(int i, int[] record, int n) {if (i == n) {return 1;}int res = 0;for (int j = 0; j < n; j++) {if (isValid(record, i, j)) {record[i] = j;res += process1(i + 1, record, n);}}return res;}public static boolean isValid(int[] record, int i, int j) {for (int k = 0; k < i; k++) {if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {return false;}}return true;}public static int num2(int n) {if (n < 1 || n > 32) {return 0;}int upperLim = n == 32 ? -1 : (1 << n) - 1;return process2(upperLim, 0, 0, 0);}public static int process2(int upperLim, int colLim, int leftDiaLim,int rightDiaLim) {if (colLim == upperLim) {return 1;}int pos = 0;int mostRightOne = 0;pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));int res = 0;while (pos != 0) {mostRightOne = pos & (~pos + 1);pos = pos - mostRightOne;res += process2(upperLim, colLim | mostRightOne,(leftDiaLim | mostRightOne) << 1,(rightDiaLim | mostRightOne) >>> 1);}return res;}public static void main(String[] args) {int n = 32;long start = System.currentTimeMillis();System.out.println(num2(n));long end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + "ms");start = System.currentTimeMillis();System.out.println(num1(n));end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + "ms");}
}

4.4馬拉車——字符串神級算法

Manacher's Algorithm 馬拉車算法操作及原理?

package advanced_001;public class Code_Manacher {public static char[] manacherString(String str) {char[] charArr = str.toCharArray();char[] res = new char[str.length() * 2 + 1];int index = 0;for (int i = 0; i != res.length; i++) {res[i] = (i & 1) == 0 ? '#' : charArr[index++];}return res;}public static int maxLcpsLength(String str) {if (str == null || str.length() == 0) {return 0;}char[] charArr = manacherString(str);int[] pArr = new int[charArr.length];int C = -1;int R = -1;int max = Integer.MIN_VALUE;for (int i = 0; i != charArr.length; i++) {pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {if (charArr[i + pArr[i]] == charArr[i - pArr[i]])pArr[i]++;else {break;}}if (i + pArr[i] > R) {R = i + pArr[i];C = i;}max = Math.max(max, pArr[i]);}return max - 1;}public static void main(String[] args) {String str1 = "abc1234321ab";System.out.println(maxLcpsLength(str1));}}

?問題：查找一個字符串的??最長回文子串

首先敘述什么是回文子串：回文：就是對稱的字符串，或者說是正反一樣的

小問題一：請問，子串和子序列一樣么？請思考一下再往下看

?當然，不一樣。子序列可以不連續，子串必須連續。

舉個例子，”123”的子串包括1，2，3，12，23，123(一個字符串本身是自己的最長子串)，而它的子序列是任意選出元素組成，他的子序列有1，2，3，12，13，23，123，””,空其實也算，但是本文主要是想敘述回文，沒意義。

小問題二：長度為n的字符串有多少個子串？多少個子序列？

?子序列，每個元素都可以選或者不選，所以有2的n次方個子序列（包括空）

子串：以一位置開頭，有n個子串，以二位置開頭，有n-1個子串，以此類推，我們發現，這是一個等差數列，而等差序列求和，有n*(n+1)/2個子串(不包括空)。

(這里有一個思想需要注意，遇到等差數列求和，基本都是o(n^2)級別的)

4.4一、分析枚舉的效率

好，我們來分析一下暴力枚舉的時間復雜度，上文已經提到過，一個字符串的所有子串，數量是o(n^2)級別，所以光是枚舉出所有情況時間就是o(n^2)，每一種情況，你要判斷他是不是回文的話，還需要o(n)，情況數和每種情況的時間，應該乘起來，也就是說，枚舉時間要o(n^3)，效率太低。

4.4二、初步優化

思路：我們知道，回文全是對稱的，每個回文串都會有自己的對稱軸，而兩邊都對稱。我們如果從對稱軸開始，向兩邊闊，如果總相等，就是回文，擴到兩邊不相等的時候，以這個對稱軸向兩邊擴的最長回文串就找到了。

舉例：1 2 1 2 1 2 1 1 1

我們用每一個元素作為對稱軸，向兩邊擴

0位置，左邊沒東西，只有自己；

1位置，判斷左邊右邊是否相等，1=1所以接著擴，然后左邊沒了，所以以1位置為對稱軸的最長回文長度就是3；

2位置，左右都是2，相等，繼續，左右都是1，繼續，左邊沒了，所以最長為5

3位置，左右開始擴，1=1，2=2，1=1，左邊沒了，所以長度是7

如此把每個對稱軸擴一遍，最長的就是答案，對么？

你要是點頭了。。。自己扇自己兩下。

還有偶回文呢，，比如1221，123321.這是什么情況呢？這個對稱軸不是一個具體的數，因為人家是偶回文。

問題三：怎么用對稱軸向兩邊擴的方法找到偶回文？（容易操作的）

我們可以在元素間加上一些符號，比如/1/2/1/2/1/2/1/1/1/，這樣我們再以每個元素為對稱軸擴就沒問題了，每個你加進去的符號都是一個可能的偶數回文對稱軸，此題可解。。。因為我們沒有錯過任何一個可能的對稱軸，不管是奇數回文還是偶數回文。

那么請問，加進去的符號，有什么要求么？是不是必須在原字符中沒出現過？請思考

其實不需要的，大家想一下，不管怎么擴，原來的永遠和原來的比較，加進去的永遠和加進去的比較。（不舉例子說明了，自己思考一下）

好，分析一波時間效率吧，對稱軸數量為o(n)級別，每個對稱軸向兩邊能擴多少？最多也就o(n)級別，一共長度才n; 所以n*n是o(n^2) ??(最大能擴的位置其實也是兩個等差數列，這么理解也是o(n^2)，用到剛講的知識)

小結：

這種方法把原來的暴力枚舉o(n^3)變成了o(n^2),大家想一想為什么這樣更快呢？

我在kmp一文中就提到過，我們寫出暴力枚舉方法后應想一想自己做出了哪些重復計算，錯過了哪些信息，然后進行優化。

看我們的暴力方法，如果按一般的順序枚舉，012345，012判斷完，接著判斷0123，我是沒想到可以利用前面信息的方法，因為對稱軸不一樣啊，右邊加了一個元素，左邊沒加。所以剛開始，老是想找一種方法，左右都加一個元素，這樣就可以對上一次的信息加以利用了。

暴力為什么效率低？永遠是因為重復計算，舉個例子：12121211，下標從0開始，判斷1212121是否為回文串的時候，其實21212和121等串也就判斷出來了，但是我們并沒有記下結果，當枚舉到21212或者121時，我們依舊是重新嘗試了一遍。(假設主串長度為n，對稱軸越在中間，長度越小的子串，被重復嘗試的越多。中間那些點甚至重復了n次左右，本來一次搞定的事）

還是這個例子，我換一個角度敘述一下，比較直觀，如果從3號開始向兩邊擴，121，21212，最后擴到1212121，時間復雜度o(n),用枚舉的方法要多少時間？如果主串長度為n，枚舉嘗試的子串長度為，3，5，7....n,等差數列，大家讀到這里應該都知道了，等差數列求和，o(n^2)。

4.4三、Manacher原理

首先告訴大家，這個算法時間可以做到o(n),空間o(n).

好的，開始講解這個神奇的算法。

首先明白兩個概念：

最右回文邊界R：挺好理解，就是目前發現的回文串能延伸到的最右端的位置(一個變量解決）

中心c：第一個取得最右回文邊界的那個中心對稱軸；舉個例子:12121，二號元素可以擴到12121，三號元素可以擴到121，右邊界一樣，我們的中心是二號元素，因為它第一個到達最右邊界

當然，我們還需要一個數組p來記錄每一個可能的對稱軸最后擴到了哪里。

有了這么幾個東西，我們就可以開始這個神奇的算法了。

為了容易理解，我分了四種情況，依次講解：

假設遍歷到位置i，如何操作呢

1）i>R:也就是說，i以及i右邊，我們根本不知道是什么，因為從來沒擴到那里。那沒有任何優化，直接往右暴力擴唄。

（下面我們做i關于c的對稱點，i’）

2）i<R:，

三種情況：

i’的回文左邊界在c回文左邊界的里面

i’回文左邊界在整體回文的外面

?i’左邊界和c左邊界是一個元素

(怕你忘了概念，c是對稱中心，c它當初擴到了R，R是目前擴到的最右的地方，現在咱們想以i為中心，看能擴到哪里。)

按原來o(n^2)的方法，直接向兩邊暴力擴。好的，魔性的優化來了。咱們為了好理解，分情況說。首先，大家應該知道的是，i’其實有人家自己的回文長度，我們用數組p記錄了每個位置的情況，所以我們可以知道以i’為中心的回文串有多長。?

2-1）i’的回文左邊界在c回文的里面：看圖

我用這兩個括號括起來的就是這兩個點向兩邊擴到的位置，也就是i和i’的回文串，為什么敢確定i回文只有這么長？和i’一樣？我們看c，其實這個圖整體是一個回文串啊。

串內完全對稱(1是括號左邊相鄰的元素，2是右括號右邊相鄰的元素，34同理)，

?由此得出結論1：

由整體回文可知，點2=點3，點1=點4

當初i’為什么沒有繼續擴下去？因為點1！=點2。

由此得出結論2：點1！=點2?

因為前面兩個結論，所以3！=4，所以i也就到這里就擴不動了。而34中間肯定是回文，因為整體回文，和12中間對稱。

2-2）i’回文左邊界在整體回文的外面了：看圖

?這時，我們也可以直接確定i能擴到哪里，請聽分析：

當初c的大回文，擴到R為什么就停了？因為點2！=點4----------結論1；

2’為2關于i’的對稱點，當初i’左右為什么能繼續擴呢？說明點2=點2’---------結論2；

由c回文可知2’=3，由結論2可知點2=點2’，所以2=3；

但是由結論一可知，點2！=點4，所以推出3！=4，所以i擴到34為止了，34不等。

而34中間那一部分，因為c回文，和i’在內部的部分一樣，是回文，所以34中間部分是回文。?

2-3）最后一種當然是i’左邊界和c左邊界是一個元素

?點1！=點2，點2=點3，就只能推出這些，只知道34中間肯定是回文，外邊的呢？不知道啊，因為不知道3和4相不相等，所以我們得出結論：點3點4內肯定是，繼續暴力擴。

原理及操作敘述完畢，不知道我講沒講明白。。。

4.4四、代碼及復雜度分析

?看代碼大家是不是覺得不像o(n)？其實確實是的，來分析一波。。

首先，我們的i依次往下遍歷，而R（最右邊界）從來沒有回退過吧？其實當我們的R到了最右邊，就可以結束了。再不濟i自己也能把R一個一個懟到最右

我們看情況一和四，R都是以此判斷就向右一個，移動一次需要o(1)

我們看情況二和三，直接確定了p[i]，根本不用擴，直接遍歷下一個元素去了，每個元素o(1).

綜上，由于i依次向右走，而R也沒有回退過，最差也就是i和R都到了最右邊，而讓它們移動一次的代價都是o(1)的，所以總體o(n)

可能大家看代碼依舊有點懵，其實就是code整合了一下，我們對于情況23，雖然知道了它肯定擴不動，但是我們還是給它一個起碼是回文的范圍，反正它擴一下就沒擴動，不影響時間效率的。而情況四也一樣，給它一個起碼是回文，不用驗證的區域，然后接著擴，四和二三的區別就是。二三我們已經心中有B樹，它肯定擴不動了，而四確實需要接著嘗試。

（要是寫四種情況當然也可以。。但是我懶的寫，太多了。便于理解分了四種情況解釋，code整合后就是這樣子）????

我真的想象不到當初發明這個算法的人是怎么想到的，向他致敬。