本文代碼實現基本按照《數據結構》課本目錄順序，外加大量的復雜算法實現，一篇文章足夠。能換你一個收藏了吧？
?當然如果落下什么了歡迎大家評論指出
目錄
順序存儲線性表實現?
單鏈表不帶頭標準c語言實現
單鏈表不帶頭壓縮c語言實現
約瑟夫環-(數組、循環鏈表、數學)?
線性表表示集合
?線性表實現一元多項式操作
鏈表環問題
?
移除鏈表元素
回文鏈表
鏈表表示整數，相加
LRU
LFU
合并鏈表
反轉鏈表
?反轉鏈表2
對鏈表排序
旋轉鏈表
?數組實現棧
鏈表實現棧
數組實現隊列
鏈表實現隊列
雙棧的實現
?棧/隊列 互相模擬實現
棧的排序
棧——括號匹配
棧——表達式求值?
借漢諾塔理解棧與遞歸
單調棧
雙端單調隊列
?單調隊列優化的背包問題
01背包問題?
完全背包問題?
多重背包問題?
?串的定長表示
串的堆分配實現
KMP
一、引子
二、分析總結
三、基本操作
四、原理
五、復雜度分析
Manacher
小問題一：請問，子串和子序列一樣么？請思考一下再往下看
小問題二：長度為n的字符串有多少個子串？多少個子序列？
一、分析枚舉的效率
二、初步優化
問題三：怎么用對稱軸向兩邊擴的方法找到偶回文？（容易操作的）
那么請問，加進去的符號，有什么要求么？是不是必須在原字符中沒出現過？請思考
小結：
三、Manacher原理
假設遍歷到位置i，如何操作呢
四、代碼及復雜度分析
前綴樹
后綴樹/后綴數組
后綴樹：后綴樹，就是把一串字符的所有后綴保存并且壓縮的字典樹。
?
相對于字典樹來說，后綴樹并不是針對大量字符串的，而是針對一個或幾個字符串來解決問題。比如字符串的回文子串，兩個字符串的最長公共子串等等。
后綴數組：就是把某個字符串的所有后綴按照字典序排序后的數組。（數組中保存起始位置就好了，結束位置一定是最后）
AC自動機
數組缺失
二叉樹遍歷
前序
中序
后序
進一步思考
二叉樹序列化/反序列化
先序中序后序兩兩結合重建二叉樹
先序遍歷
中序遍歷
后序遍歷
層次遍歷
輸入某二叉樹的前序遍歷和中序遍歷的結果，請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重復的數字。例如輸入前序遍歷序列{1,2,4,7,3,5,6,8}和中序遍歷序列{4,7,2,1,5,3,8,6}，則重建二叉樹并返回。
輸入某二叉樹的后序遍歷和中序遍歷的結果，請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重復的數字
輸入某二叉樹的后序遍歷和先序遍歷的結果，請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重復的數字
先序中序數組推后序數組
二叉樹遍歷
遍歷命名
方法1：我們可以重建整棵樹：
https://blog.csdn.net/hebtu666/article/details/84322113
方法2：我們可以不用重建，直接得出：
根據數組建立平衡二叉搜索樹
java整體打印二叉樹
判斷平衡二叉樹
判斷完全二叉樹
判斷二叉搜索樹
二叉搜索樹實現
堆的簡單實現
堆應用例題三連
一個數據流中，隨時可以取得中位數。
金條
項目最大收益（貪心問題）
?并查集實現
并查集入門三連：HDU1213 POJ1611 POJ2236
HDU1213
POJ1611
?POJ2236
線段樹簡單實現
功能：一樣的，依舊是查詢和改值。
查詢[s,t]之間最小的數。修改某個值。
那我們繼續說，如何查詢。
如何更新？
?樹狀數組實現
最大搜索子樹
morris遍歷
最小生成樹
拓撲排序
最短路
?
簡單迷宮問題
深搜DFS\廣搜BFS?
?皇后問題
一般思路：
優化1：
優化2：
二叉搜索樹實現
Abstract Self-Balancing Binary Search Tree
?
二叉搜索樹
概念引入
AVL樹
紅黑樹
size balance tree
伸展樹
Treap
最簡單的旋轉
帶子樹旋轉
代碼實現
AVL Tree
前言
二叉搜索樹
AVL Tree
旋轉
旋轉總結
單向右旋平衡處理LL：
單向左旋平衡處理RR：
雙向旋轉（先左后右）平衡處理LR：
雙向旋轉（先右后左）平衡處理RL：
深度的記錄
單個節點的深度更新
寫出旋轉代碼
總寫調整方法
插入完工
刪除
直觀表現程序
跳表介紹和實現
c語言實現排序和查找所有算法
?
?
順序存儲線性表實現?
在計算機中用一組地址連續的存儲單元依次存儲線性表的各個數據元素,稱作線性表的順序存儲結構。
?
順序存儲結構的主要優點是節省存儲空間，因為分配給數據的存儲單元全用存放結點的數據（不考慮c/c++語言中數組需指定大小的情況），結點之間的邏輯關系沒有占用額外的存儲空間。采用這種方法時，可實現對結點的隨機存取，即每一個結點對應一個序號，由該序號可以直接計算出來結點的存儲地址。但順序存儲方法的主要缺點是不便于修改，對結點的插入、刪除運算時，可能要移動一系列的結點。
優點：隨機存取表中元素。缺點：插入和刪除操作需要移動元素。
?
線性表中數據元素之間的關系是一對一的關系，即除了第一個和最后一個數據元素之外，其它數據元素都是首尾相接的（注意，這句話只適用大部分線性表，而不是全部。比如，循環鏈表邏輯層次上也是一種線性表（存儲層次上屬于鏈式存儲），但是把最后一個數據元素的尾指針指向了首位結點）。
給出兩種基本實現：
/*
靜態順序存儲線性表的基本實現
*/#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define LIST_INITSIZE 100
#define ElemType int
#define Status int
#define OK 1
#define ERROR 0typedef struct
{ElemType elem[LIST_INITSIZE];int length;
}SqList;//函數介紹
Status InitList(SqList *L); //初始化
Status ListInsert(SqList *L, int i,ElemType e);//插入
Status ListDelete(SqList *L,int i,ElemType *e);//刪除
void ListPrint(SqList L);//輸出打印
void DisCreat(SqList A,SqList *B,SqList *C);//拆分(按正負)，也可以根據需求改
//雖然思想略簡單，但是要寫的沒有錯誤，還是需要鍛煉coding能力的Status InitList(SqList *L)
{L->length = 0;//長度為0return OK;
}Status ListInsert(SqList *L, int i,ElemType e)
{int j;if(i<1 || i>L->length+1)return ERROR;//判斷非法輸入if(L->length == LIST_INITSIZE)//判滿{printf("表已滿");//提示return ERROR;//返回失敗}for(j = L->length;j > i-1;j--)//從后往前覆蓋，注意i是從1開始L->elem[j] = L->elem[j-1];L->elem[i-1] = e;//在留出的位置賦值(L->length)++;//表長加1return OK;//反回成功
}Status ListDelete(SqList *L,int i,ElemType *e)
{int j;if(i<1 || i>L->length)//非法輸入/表空return ERROR;*e = L->elem[i-1];//為了返回值for(j = i-1;j <= L->length;j++)//從前往后覆蓋L->elem[j] = L->elem[j+1];(L->length)--;//長度減1return OK;//返回刪除值
}void ListPrint(SqList L)
{int i;for(i = 0;i < L.length;i++)printf("%d ",L.elem[i]);printf("\n");//為了美觀
}void DisCreat(SqList A,SqList *B,SqList *C)
{int i;for(i = 0;i < A.length;i++)//依次遍歷A中元素{if(A.elem[i]<0)//判斷ListInsert(B,B->length+1,A.elem[i]);//直接調用插入函數實現尾插elseListInsert(C,C->length+1,A.elem[i]);}
}int main(void)
{//復制的SqList L;SqList B, C;int i;ElemType e;ElemType data[9] = {11,-22,33,-3,-88,21,77,0,-9};InitList(&L);InitList(&B);InitList(&C);for (i = 1; i <= 9; i++)ListInsert(&L,i,data[i-1]);printf("插入完成后L = : ");ListPrint(L);ListDelete(&L,1,&e);printf("刪除第1個后L = : ");ListPrint(L);DisCreat(L , &B, &C);printf("拆分L后B = : ");ListPrint(B);printf("拆分L后C = : ");ListPrint(C);printf("拆分L后L = : ");ListPrint(L);
}靜態：長度固定
動態：不夠存放可以加空間（搬家）
?
/*
子任務名任務:1_2 動態順序存儲線性表的基本實現
*/#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
#define Status int
#define OVERFLOW -1
#define OK 1
#define ERROR 0
#define ElemType inttypedef struct
{ElemType * elem;int length;int listsize;
}SqList;
//函數介紹
Status InitList(SqList *L); //初始化
Status ListInsert(SqList *L, int i,ElemType e);//插入
Status ListDelete(SqList *L,int i,ElemType *e);//刪除
void ListPrint(SqList L);//輸出打印
void DeleteMin(SqList *L);//刪除最小Status InitList(SqList *L)
{L->elem = (ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType));//申請100空間if(!L->elem)//申請失敗return ERROR;L->length = 0;//長度0L->listsize = LIST_INIT_SIZE;//容量100return OK;//申請成功
}Status ListInsert(SqList *L,int i,ElemType e)
{int j;ElemType *newbase;if(i<1 || i>L->length+1)return ERROR;//非法輸入if(L->length >= L->listsize)//存滿了，需要更大空間{newbase = (ElemType*)realloc(L->elem,(L->listsize+LISTINCREMENT)*sizeof(ElemType));//大10的空間if(!newbase)//申請失敗return ERROR;L->elem = newbase;//調指針L->listsize+= LISTINCREMENT;//新容量}for(j=L->length;j>i-1;j--)//從后往前覆蓋L->elem[j] = L->elem[j-1];L->elem[i-1] = e;//在留出的位置賦值L->length++;//長度+1return OK;
}Status ListDelete(SqList *L,int i,ElemType *e)
{int j;if(i<1 || i>L->length)//非法輸入/表空return ERROR;*e = L->elem[i-1];//為了返回值for(j = i-1;j <= L->length;j++)//從前往后覆蓋L->elem[j] = L->elem[j+1];(L->length)--;//長度減1return OK;//返回刪除值
}void ListPrint(SqList L)
{int i;for(i=0;i<L.length;i++)printf("%d ",L.elem[i]);printf("\n");//為了美觀
}void DeleteMin(SqList *L)
{//表空在Listdelete函數里判斷int i;int j=0;//最小值下標ElemType *e;for(i=0;i<L->length;i++)//尋找最小{if(L->elem[i] < L->elem[j])j=i;}ListDelete(L,j+1,&e);//調用刪除，注意j要+1
}int main(void)
{SqList L;int i;ElemType e;ElemType data[9] = {11,-22,-33,3,-88,21,77,0,-9};InitList(&L);for (i = 1; i <= 9; i++){ListInsert(&L,i,data[i-1]);}printf("插入完成后 L = : ");ListPrint(L);ListDelete(&L, 2, &e);printf("刪除第 2 個后L = : ");ListPrint(L);DeleteMin(&L);printf("刪除L中最小值后L = : ");ListPrint(L);DeleteMin(&L);printf("刪除L中最小值后L = : ");ListPrint(L);DeleteMin(&L);printf("刪除L中最小值后L = : ");ListPrint(L);
}單鏈表不帶頭標準c語言實現
?
鏈表是一種物理存儲單元上非連續、非順序的存儲結構，數據元素的邏輯順序是通過鏈表中的指針鏈接次序實現的。鏈表由一系列結點（鏈表中每一個元素稱為結點）組成，結點可以在運行時動態生成。每個結點包括兩個部分：一個是存儲數據元素的數據域，另一個是存儲下一個結點地址的指針域。 相比于線性表順序結構，操作復雜。由于不必須按順序存儲，鏈表在插入的時候可以達到O(1)的復雜度，比另一種線性表順序表快得多，但是查找一個節點或者訪問特定編號的節點則需要O(n)的時間，而線性表和順序表相應的時間復雜度分別是O(logn)和O(1)。
使用鏈表結構可以克服數組鏈表需要預先知道數據大小的缺點，鏈表結構可以充分利用計算機內存空間，實現靈活的內存動態管理。但是鏈表失去了數組隨機讀取的優點，同時鏈表由于增加了結點的指針域，空間開銷比較大。鏈表最明顯的好處就是，常規數組排列關聯項目的方式可能不同于這些數據項目在記憶體或磁盤上順序，數據的存取往往要在不同的排列順序中轉換。鏈表允許插入和移除表上任意位置上的節點，但是不允許隨機存取。鏈表有很多種不同的類型：單向鏈表，雙向鏈表以及循環鏈表。
?
下面給出不帶頭的單鏈表標準實現：
定義節點：
typedef struct node
{ int data;struct node * next;
}Node;尾插：
void pushBackList(Node ** list, int data)
{ Node * head = *list;Node * newNode = (Node *)malloc(sizeof(Node));//申請空間newNode->data = data; newNode->next = NULL;if(*list == NULL)//為空*list = newNode;else//非空{while(head ->next != NULL)head = head->next;head->next = newNode;}
}插入：
int insertList(Node ** list, int index, int data)
{int n;int size = sizeList(*list); Node * head = *list; Node * newNode, * temp;if(index<0 || index>size) return 0;//非法newNode = (Node *)malloc(sizeof(Node)); //創建新節點newNode->data = data; newNode->next = NULL;if(index == 0) //頭插{newNode->next = head; *list = newNode; return 1; }for(n=1; n<index; n++) //非頭插head = head->next;if(index != size) newNode->next = head->next; //鏈表尾部next不需指定head->next = newNode; return 1;
}
按值刪除：
void deleteList(Node ** list, int data)
{ Node * head = *list; Node * temp; while(head->next!=NULL) { if(head->next->data != data) { head=head->next; continue; } temp = head->next;if(head->next->next == NULL) //尾節點刪除head->next = NULL; else head->next = temp->next; free(temp);} head = *list; if(head->data == data) //頭結點刪除{ temp = head; *list = head->next; head = head->next; free(temp); }
}
打印：
void printList(Node * head)
{ Node * temp = head; for(; temp != NULL; temp=temp->next) printf("%d ", temp->data); printf("\n");
}清空：
void freeList(Node ** list)
{ Node * head = *list; Node * temp = NULL; while(head != NULL) //依次釋放{ temp = head; head = head->next; free(temp); } *list = NULL; //置空
}別的也沒啥了，都是基本操作
有些代碼要分情況，很麻煩，可讀性較強吧
?
單鏈表不帶頭壓縮c語言實現
?
?
?注：單追求代碼簡潔，所以寫法可能有點不標準。
//第一次拿c開始寫數據結構，因為自己寫的，追求代碼量少，和學院ppt不太一樣。有錯請指出
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct node//定義節點
{int data;struct node * next;
}Node;?
//函數介紹
void printlist(Node * head)//打印鏈表
int lenlist(Node * head)//返回鏈表長度
void insertlist(Node ** list,int data,int index)//插入元素
void pushback(Node ** head,int data)//尾部插入
void freelist(Node ** head)//清空鏈表
void deletelist(Node ** list,int data)//刪除元素
Node * findnode(Node ** list,int data)//查找
void change(Node ** list,int data,int temp)//改變值打印
void printlist(Node * head)//打印鏈表
{for(;head!=NULL;head=head->next) printf("%d ",head->data);printf("\n");//為了其他函數打印，最后換行
}鏈表長度
int lenlist(Node * head)//返回鏈表長度
{int len;Node * temp = head;for(len=0; temp!=NULL; len++) temp=temp->next;return len;
}插入元素
void insertlist(Node ** list,int data,int index)//插入元素，用*list將head指針和next統一表示
{if(index<0 || index>lenlist(*list))return;//判斷非法輸入Node * newnode=(Node *)malloc(sizeof(Node));//創建newnode->data=data;newnode->next=NULL;while(index--)list=&((*list)->next);//插入newnode->next=*list;*list=newnode;
}尾部增加元素
void pushback(Node ** head,int data)//尾插，同上
{Node * newnode=(Node *)malloc(sizeof(Node));//創建newnode->data=data;newnode->next=NULL;while(*head!=NULL)head=&((*head)->next);//插入*head=newnode;
}清空鏈表
void freelist(Node ** head)//清空鏈表
{Node * temp=*head;Node * ttemp;*head=NULL;//指針設為空while(temp!=NULL)//釋放{ttemp=temp;temp=temp->next;free(ttemp);}
}刪除
void deletelist(Node ** list,int data)//刪除鏈表節點
{Node * temp;//作用只是方便freewhile((*list)->data!=data && (*list)->next!=NULL)list=&((*list)->next);if((*list)->data==data){temp=*list;*list=(*list)->next;free(temp);}
}查找
Node * findnode(Node ** list,int data)//查找，返回指向節點的指針，若無返回空
{while((*list)->data!=data && (*list)!=NULL) list=&((*list)->next);return *list;
}改值
void change(Node ** list,int data,int temp)//改變
{while((*list)->data!=data && (*list)->next!=NULL)list=&((*list)->next);if((*list)->data==data)(*list)->data=temp;
}?
最后測試
int main(void)//測試
{Node * head=NULL;Node ** gg=&head;int i;for(i=0;i<10;i++)pushback(gg,i);printf("鏈表元素依次為: ");printlist(head);printf("長度為%d\n",lenlist(head));freelist(gg);printf("釋放后長度為%d\n",lenlist(head));for(i=0;i<10;i++)pushback(gg,i);deletelist(gg,0);//頭deletelist(gg,9);//尾deletelist(gg,5);deletelist(gg,100);//不存在printf("再次創建鏈表，刪除節點后\n");printlist(head);freelist(gg);for(i=0;i<5;i++)pushback(gg,i);insertlist(gg,5,0);//頭insertlist(gg,5,5);insertlist(gg,5,7);//尾insertlist(gg,5,10);//不存在printlist(head);printf("找到%d\n把3變為100",*findnode(gg,5));change(gg,3,100);change(gg,11111,1);//不存在printlist(head);
}
約瑟夫環-(數組、循環鏈表、數學)?
約瑟夫環（約瑟夫問題）是一個數學的應用問題：已知n個人（以編號1，2，3...n分別表示）圍坐在一張圓桌周圍。從編號為k的人開始報數，數到m的那個人出列；他的下一個人又從1開始報數，數到m的那個人又出列；依此規律重復下去，直到圓桌周圍的人全部出列。
?
約瑟夫環運作如下：
1、一群人圍在一起坐成環狀（如：N）
2、從某個編號開始報數（如：S）
3、數到某個數（如：M）的時候，此人出列，下一個人重新報數
4、一直循環，直到所有人出列??，約瑟夫環結束
模擬過程，求出最后的人。
把數組看成一個環，從第s個元素開始按m-1間隔刪除元素，重復過程，直到元素全部去掉。
?
void Josephus(int a[],int n,int m,int s)
{int i,j;int k=n;for(i=0;i<n;i++)a[i]=i+1;//編號i=(s+n-1)%n;while(k){for(j=1;j<m;j++)i=(i+1)%k;//依次報數，頭尾相連printf("%d\n",a[i]);//出局for(j=i+1;j<k;j++)a[j-1]=a[j];//刪除本節點k--;}//模擬結束，最后輸出的就是留下的人
}?
可以用帶頭單循環鏈表來求解：
也是一樣的，只是實現不同，給出核心代碼：
while(k){for(j=1;j<m;j++){pr=p;p=p->link;if(p==head)//頭結點跳過{pr=p;p=p->link;}}k--;//打印pr->link=p->link;//刪結點free(p);p=pr->link;//從下一個繼續}雙向循環鏈表也可以解，和單鏈表類似，只是不需要保持前趨指針。
?
數學可解：
效率最高
int check_last_del(int n,int m)
{int i = 1;int ret = 0;for (i = 2; i<=n;i++)ret = (ret + m) %i;return ret+1;//因為ret是從0到n-1，最后別忘了加1。
}
線性表表示集合
集合我們高中都學過吧？
最重要的幾個特點：元素不能重復、各個元素之間沒有關系、沒有順序
集合內的元素可以是單元素或者是集合。
對集合的操作：交集并集差集等，還有對自身的加減等。
需要頻繁的加減元素，所以順序存儲效率較低，但是我們還是說一下是怎么實現的：
? ? 用01向量表示集合，因為現實中任何一個有窮集合都能對應到一個0、1、2.....n這么一個序列中。所以可以對應過來，每位的01代表這個元素存在與否即可。
鏈接存儲表示使用有序鏈表來實現，雖然集合是無序的，但是我們的鏈表可以是有序的。可以按升序排列。而鏈表理論上可以無限增加，所以鏈表可以表示無限集。
下面我們來實現一下：
我們定義一個節點：
typedef int ElemType;
typedef struct SetNode{//節點定義ElemType data;//數據struct SetNode * link;
}*LinkedSet//集合定義然后要實現那些操作了，首先想插入吧：我們對于一個新元素，查找集合中是否存在，存在就不插入，不存在就插入到查找失敗位置。
刪除也簡單，查找存在就刪除。
?
我們說兩個集合的操作：
求兩個集合的并：
兩個鏈表，都是升序。把他們去重合并即可。
其實和鏈表歸并的merge過程是一樣的，只是相等的時候插入一個，兩個指針都向后走就行了。
我就再寫一遍吧。
void UnionSet(LinkedSet & A,LinkedSet & B,LinkedSet & C)
{SetNode *pa=A->link,*pb=B->link,*pc=C;while(pa && pb)//都不為空{if(pa->data==pb->data)//相等，插一次，兩邊向后{pc->link=new SetNode;pc->data=pa->data;pa=pa->link;pb=pb->link;}else if(pa->data<pb->data)//插小的，小的向后{pc->link=new SetNode;pc->data=pa->data;pa=pa->link;}else{pc->link=new SetNode;pc->data=pb->data;pb=pb->link;}pc=pc->link;//注意指針}if(pa)p=pa;//剩下的接上else p=pb;//只執行一個while(p)//依次復制{pc->link=new SetNode;pc->data=p->data;pc=pc->link;p=p->link;}pc->link=NULL;
}求兩個集合的交，更簡單，還是這三種情況，誰小誰向后，相等才插入。
void UnionSet(LinkedSet & A,LinkedSet & B,LinkedSet & C)
{SetNode *pa=A->link,*pb=B->link,*pc=C;while(pa && pb)//都不為空{if(pa->data==pb->data)//相等，插一次，兩邊向后{pc->link=new SetNode;pc->data=pa->data;pa=pa->link;pb=pb->link;pc=pc->link;//注意指針,就不是每次都向后了，只有插入才向后}else if(pa->data<pb->data)//小的向后{pa=pa->link;}else{pb=pb->link;}}pc->link=NULL;
}求兩個集合的差：高中可能沒學這個概念，其實就是A-B，就是B中的元素，A都不能有了。
運算你可以把B元素全過一遍，A中有就去掉，但是這樣時間復雜度太高了，我們需要O(A+B)而不是O(A*B)
因為有序，很好操作，還是兩個指針，
如果AB相同，都向后移。
或者，B小，B就向后移。
如果A小，說明B中不含這個元素，我們把它復制到結果鏈表里。
?
思想還行，實在懶得寫了，有時間再說吧。
?線性表實現一元多項式操作
?
數組存放：
不需要記錄冪，下標就是。
比如1，2，3，5表示1+2x+3x^2+5x^3
有了思路，我們很容易定義結構
typedef struct node{float * coef;//系數數組int maxSize;//最大容量int order;//最高階數
}Polynomial;先實現求和：我們想求兩個式子a+b，結果存在c中。
邏輯很簡單，就是相加啊。
void Add(Polynomial & A,Polynomial & B,Polynomial & C)
{int i;int m=A.order;int n=B.order;for(i=0;i<=m && i<=n;i++)//共有部分加一起C.coef[i]=A.coef[i]+B.coef[i];while(i<=m)//只會執行一個，作用是把剩下的放入cC.coef[i]=A.coef[i];while(i<=n)C.coef[i]=B.coef[i];C.order=(m>n)?m:n;//等于較大項
}實現乘法：
我們思考一下，兩個多項式怎么相乘？
把a中每一項都和b中每一項乘一遍就好了。
高中知識
?
void Mul(Polynomial & A,Polynomial & B,Polynomial & C)
{int i;int m=A.order;int n=B.order;if(m+n>C.maxSize){printf("超限");return;}for(i=0;i<=m+n;i++)//注意范圍，是最高項的冪加起來C.coef[i]=0.0;for(i=0;i<=m;i++){for(j=0;j<=n;j++){C.coef[i+j]+=A.coef[i]*B.coef[j];}}C.order=m+n;//注意范圍，是最高項的冪加起來
}?
利用數組存放雖然簡單，但是當冪相差很大時，會造成空間上的嚴重浪費（包括時間也是），所以我們考慮采用鏈表存儲。
?
我們思考一下如何存儲和做運算。
?
我們肯定要再用一個變量記錄冪了。每個節點記錄系數和指數。
考慮如何相加：
對于c，其實剛開始是空的，我們首先要實現一個插入功能，然后，遍歷a和b，進一步利用插入函數來不斷尾插。
因為a和b都是升冪排列，所以相加的時候，絕對不會發生結果冪小而后遇到的情況，所以放心的一直插入就好了。
具體實現也比較好想：a和b冪相等就加起來，不等就小的單獨插入，然后指針向后移。
加法就放老師寫的代碼吧，很漂亮的代碼：（沒和老師商量，希望不會被打）
老師原地插的，都一樣都一樣
老師原文：http://www.edu2act.net/article/shu-ju-jie-gou-xian-xing-biao-de-jing-dian-ying-yong/
void AddPolyn(polynomial &Pa, polynomial &Pb)//多項式的加法：Pa = Pa + Pb,利用兩個多項式的結點構成“和多項式”。
{LinkList ha = Pa; //ha和hb分別指向Pa和Pb的頭指針LinkList hb = Pb;LinkList qa = Pa->next;LinkList qb = Pb->next; //ha和hb分別指向pa和pb的前驅while (qa && qb) //如果qa和qb均非空{float sum = 0.0;term a = qa->data;term b = qb->data;switch (cmp(a,b)){case -1: //多項式PA中當前結點的指數值小ha = qa;qa = qa->next;break;case 0: //兩者指數值相等sum = a.coef + b.coef;if(sum != 0.0){ //修改多項式PA中當前結點的系數值qa->data.coef = sum;ha = qa;}else{ //刪除多項式PA中當前結點DelFirst(ha, qa);free(qa);}DelFirst(hb, qb);free(qb);qb = hb->next;qa = ha->next;break;case 1:DelFirst(hb, qb);InsFirst(ha, qb);qb = hb->next;ha = ha->next;break;}//switch}//whileif(!ListEmpty(Pb))Append(Pa,qb);DestroyList(hb);}//AddPolyn對于乘法，我們就不能一直往后插了，因為遍歷兩個式子，可能出現冪變小的情況。所以我們要實現一個插入函數，如果c中有這一項，就加起來，沒這一項就插入。
我們先實現插入函數：（哦，對了，我沒有像老師那樣把系數和指數再定義一個結構體，都放一起了。還有next我寫的link，還有點別的不一樣，都無傷大雅，絕對能看懂）
void Insert(Polynomial &L,float c,int e)//系數c，指數e
{Term * pre=L;Term * p=L->link;while(p && p->exp<e)//查找{pre=p;p=p->link;}if(p->exp==e)//如果有這一項{if(p->coef+c)//如果相加是0了，就刪除節點{pre->link=p->link;free(p);}else//相加不是0，就合并{p->coef+=c;}}else//如果沒這一項，插入就好了，鏈表插入寫了很多遍了{Term * pc=new Term;//創建pc->exp=e;pc->coef=c;pre->link=pc;pc->link=p; }
}插入寫完了，乘法就好實現了，還是兩個循環，遍歷a和b，只是最后調用Insert方法實現就ok
insert（c，乘系數，加冪）
?
拓展：一維數組可以模擬一元多項式。類似的，二維數組可以模擬二元多項式。實現以后有時間寫了再放鏈接。
?
?
鏈表環問題
1.判斷單鏈表是否有環
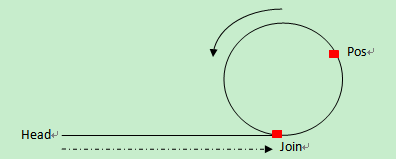
使用兩個slow, fast指針從頭開始掃描鏈表。指針slow 每次走1步，指針fast每次走2步。如果存在環，則指針slow、fast會相遇；如果不存在環，指針fast遇到NULL退出。
就是所謂的追擊相遇問題：
2.求有環單鏈表的環長
? 在環上相遇后，記錄第一次相遇點為Pos，之后指針slow繼續每次走1步，fast每次走2步。在下次相遇的時候fast比slow正好又多走了一圈，也就是多走的距離等于環長。
設從第一次相遇到第二次相遇，設slow走了len步，則fast走了2*len步，相遇時多走了一圈：
環長=2*len-len。
3.求有環單鏈表的環連接點位置
第一次碰撞點Pos到連接點Join的距離=頭指針到連接點Join的距離，因此，分別從第一次碰撞點Pos、頭指針head開始走，相遇的那個點就是連接點。
? 
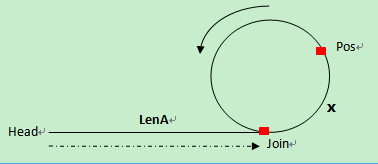
在環上相遇后，記錄第一次相遇點為Pos，連接點為Join，假設頭結點到連接點的長度為LenA，連接點到第一次相遇點的長度為x，環長為R。
第一次相遇時，slow走的長度 S =?LenA?+?x;
第一次相遇時，fast走的長度 2S =?LenA?+ n*R?+?x;
所以可以知道，LenA?+?x =??n*R; LenA = n*R -x;
4.求有環單鏈表的鏈表長
? 上述2中求出了環的長度；3中求出了連接點的位置，就可以求出頭結點到連接點的長度。兩者相加就是鏈表的長度。
?
編程實現：
下面是代碼中的例子：
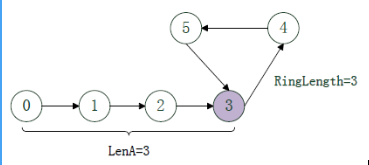
具體代碼如下：
#include <stdio.h>
#include <stdlib.h>
typedef struct node{int value;struct node *next;
}LinkNode,*Linklist;/// 創建鏈表(鏈表長度，環節點起始位置)
Linklist createList(){Linklist head = NULL;LinkNode *preNode = head;LinkNode *FifthNode = NULL;for(int i=0;i<6;i++){LinkNode *tt = (LinkNode*)malloc(sizeof(LinkNode));tt->value = i;tt->next = NULL;if(preNode == NULL){head = tt;preNode = head;}else{preNode->next =tt;preNode = tt;}if(i == 3)FifthNode = tt;}preNode->next = FifthNode;return head;
}///判斷鏈表是否有環
LinkNode* judgeRing(Linklist list){LinkNode *fast = list;LinkNode *slow = list;if(list == NULL)return NULL;while(true){if(slow->next != NULL && fast->next != NULL && fast->next->next != NULL){slow = slow->next;fast = fast->next->next;}elsereturn NULL;if(fast == slow)return fast;}
}///獲取鏈表環長
int getRingLength(LinkNode *ringMeetNode){int RingLength=0;LinkNode *fast = ringMeetNode;LinkNode *slow = ringMeetNode;for(;;){fast = fast->next->next;slow = slow->next;RingLength++;if(fast == slow)break;}return RingLength;
}///獲取鏈表頭到環連接點的長度
int getLenA(Linklist list,LinkNode *ringMeetNode){int lenA=0;LinkNode *fast = list;LinkNode *slow = ringMeetNode;for(;;){fast = fast->next;slow = slow->next;lenA++;if(fast == slow)break;}return lenA;
}///環起始點
///如果有環, 釋放空空間時需要注意.
LinkNode* RingStart(Linklist list, int lenA){if (!list || lenA <= 0){return NULL;}int i = 0;LinkNode* tmp = list;for ( ; i < lenA; ++i){if (tmp != NULL){tmp = tmp->next;}}return (i == lenA)? tmp : NULL;
}///釋放空間
int freeMalloc(Linklist list, LinkNode* ringstart){bool is_ringstart_free = false; //環起始點只能被釋放空間一次LinkNode *nextnode = NULL;while(list != NULL){nextnode = list->next;if (list == ringstart){ //如果是環起始點if (is_ringstart_free)break; //如果第二次遇到環起始點addr, 表示已經釋放完成elseis_ringstart_free = true; //記錄已經釋放一次}free(list);list = nextnode;}return 0;
}int main(){Linklist list = NULL;LinkNode *ringMeetNode = NULL;LinkNode *ringStartNode = NULL;int LenA = 0;int RingLength = 0;list = createList();ringMeetNode = judgeRing(list); //快慢指針相遇點if(ringMeetNode == NULL)printf("No Ring\n");else{printf("Have Ring\n");RingLength = getRingLength(ringMeetNode); //環長LenA = getLenA(list,ringMeetNode);printf("RingLength:%d\n", RingLength);printf("LenA:%d\n", LenA);printf("listLength=%d\n", RingLength+LenA);}ringStartNode = RingStart(list, LenA); //獲取環起始點freeMalloc(list, ringStartNode); //釋放環節點, 有環時需要注意. 采納5樓建議return 0;
}?
移除鏈表元素
?
刪除鏈表中等于給定值?val?的所有節點。
示例:
輸入: 1->2->6->3->4->5->6, val = 6
輸出: 1->2->3->4->5思路：就刪唄，注意第一個數可能會被刪
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val = x; }* }*/
class Solution {public ListNode removeElements(ListNode head, int val) {ListNode p = new ListNode(-1);p.next = head;//因為要刪除的可能是鏈表的第一個元素，所以用一個h節點來做處理ListNode h = p;while(p.next!=null) {if(p.next.val==val) {p.next = p.next.next;}else{p = p.next;} }return h.next;}
}回文鏈表
請判斷一個鏈表是否為回文鏈表。
示例 1:
輸入: 1->2
輸出: false
示例 2:
輸入: 1->2->2->1
輸出: true
進階：
你能否用?O(n) 時間復雜度和 O(1) 空間復雜度解決此題？
思路：逆置前一半，然后從中心出發開始比較即可。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val = x; }* }*/
class Solution {public boolean isPalindrome(ListNode head) {if(head == null || head.next == null) {return true;}ListNode slow = head, fast = head;ListNode pre = head, prepre = null;while(fast != null && fast.next != null) {pre = slow;slow = slow.next;fast = fast.next.next;pre.next = prepre;prepre = pre;}if(fast != null) {slow = slow.next;}while(pre != null && slow != null) {if(pre.val != slow.val) {return false;}pre = pre.next;slow = slow.next;}return true;}
}鏈表表示整數，相加
思路：就模仿加法即可。。。題目還貼心的給把順序反過來了。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val = x; }* }*/
class Solution {public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode ans=new ListNode(0);ListNode tempA=l1;ListNode tempB=l2;ListNode temp=ans;int out=0;while(tempA!=null || tempB!=null){int a=tempA!=null?tempA.val:0;int b=tempB!=null?tempB.val:0;ans.next=new ListNode((a+b+out)%10);ans=ans.next;out=(a+b+out)/10;if(tempA!=null)tempA=tempA.next;if(tempB!=null)tempB=tempB.next;}if(out!=0){ans.next=new ListNode(out); }return temp.next;}
}LRU
LRU全稱是Least?Recently Used，即最近最久未使用的意思。
LRU算法的設計原則是：如果一個數據在最近一段時間沒有被訪問到，那么在將來它被訪問的可能性也很小。也就是說，當限定的空間已存滿數據時，應當把最久沒有被訪問到的數據淘汰。（這一段是找的，讓大家理解一下什么是LRU）。
?
說一下我們什么時候見到過LRU：其實老師們肯定都給大家舉過這么個例子：你在圖書館，你把書架子里的書拿到桌子上。。但是桌子是有限的，你有時候不得不把一些書放回去。這就相當于內存和硬盤。這個例子都說過吧？
LRU就是記錄你最長時間沒看過的書，就把它放回去。在cache那里見過吧
?
然后最近在研究redis，又看到了這個LRU，所以就想寫一下吧。
題目：設計一個結構，這個結構可以查詢K-V，但是容量有限，當存不下的時候就要把用的年代最久遠的那個東西扔掉。
其實思路很簡單，我們維護一個雙向鏈表即可，get也就是使用了，我們就把把它提到最安全的位置。新來的KV就依次放即可。
我們就先寫這個雙向鏈表結構
先寫節點結構：
public static class Node<V> {public V value;public Node<V> last;//前public Node<V> next;//后public Node(V value) {this.value = value;}}然后寫雙向鏈表結構： 我們沒必要把鏈表操作都寫了，分析一下，我們只有三個操作：
1、加節點
2、使用了某個節點就把它調到尾，代表優先級最高
3、把優先級最低的移除，也就是去頭部
（不會的，翻我之前的鏈表操作都有寫）
public static class NodeDoubleLinkedList<V> {private Node<V> head;//頭private Node<V> tail;//尾public NodeDoubleLinkedList() {this.head = null;this.tail = null;}public void addNode(Node<V> newNode) {if (newNode == null) {return;}if (this.head == null) {//頭空this.head = newNode;this.tail = newNode;} else {//頭不空this.tail.next = newNode;newNode.last = this.tail;//注意讓本節點前指針指向舊尾this.tail = newNode;//指向新尾}}
/*某個點移到最后*/public void moveNodeToTail(Node<V> node) {if (this.tail == node) {//是尾return;}if (this.head == node) {//是頭this.head = node.next;this.head.last = null;} else {//中間node.last.next = node.next;node.next.last = node.last;}node.last = this.tail;node.next = null;this.tail.next = node;this.tail = node;}
/*刪除第一個*/public Node<V> removeHead() {if (this.head == null) {return null;}Node<V> res = this.head;if (this.head == this.tail) {//就一個this.head = null;this.tail = null;} else {this.head = res.next;res.next = null;this.head.last = null;}return res;}}鏈表操作封裝完了就要實現這個結構了。
具體思路代碼注釋
public static class MyCache<K, V> {//為了kv or vk都能查private HashMap<K, Node<V>> keyNodeMap;private HashMap<Node<V>, K> nodeKeyMap;//用來做優先級private NodeDoubleLinkedList<V> nodeList;private int capacity;//容量public MyCache(int capacity) {if (capacity < 1) {//你容量連1都不給，搗亂呢throw new RuntimeException("should be more than 0.");}this.keyNodeMap = new HashMap<K, Node<V>>();this.nodeKeyMap = new HashMap<Node<V>, K>();this.nodeList = new NodeDoubleLinkedList<V>();this.capacity = capacity;}public V get(K key) {if (this.keyNodeMap.containsKey(key)) {Node<V> res = this.keyNodeMap.get(key);this.nodeList.moveNodeToTail(res);//使用過了就放到尾部return res.value;}return null;}public void set(K key, V value) {if (this.keyNodeMap.containsKey(key)) {Node<V> node = this.keyNodeMap.get(key);node.value = value;//放新vthis.nodeList.moveNodeToTail(node);//我們認為放入舊key也是使用過} else {Node<V> newNode = new Node<V>(value);this.keyNodeMap.put(key, newNode);this.nodeKeyMap.put(newNode, key);this.nodeList.addNode(newNode);//加進去if (this.keyNodeMap.size() == this.capacity + 1) {this.removeMostUnusedCache();//放不下就去掉優先級最低的}}}private void removeMostUnusedCache() {//刪除頭Node<V> removeNode = this.nodeList.removeHead();K removeKey = this.nodeKeyMap.get(removeNode);//刪除掉兩個map中的記錄this.nodeKeyMap.remove(removeNode);this.keyNodeMap.remove(removeKey);}}LFU
請你為 最不經常使用（LFU）緩存算法設計并實現數據結構。可以自行百度介紹，非常著名的結構
實現 LFUCache 類：
LFUCache(int capacity) - 用數據結構的容量?capacity 初始化對象
int get(int key)?- 如果鍵存在于緩存中，則獲取鍵的值，否則返回 -1。
void put(int key, int value)?- 如果鍵已存在，則變更其值；如果鍵不存在，請插入鍵值對。當緩存達到其容量時，則應該在插入新項之前，使最不經常使用的項無效。在此問題中，當存在平局（即兩個或更多個鍵具有相同使用頻率）時，應該去除 最久未使用 的鍵。
注意「項的使用次數」就是自插入該項以來對其調用 get 和 put 函數的次數之和。使用次數會在對應項被移除后置為 0 。
為了確定最不常使用的鍵，可以為緩存中的每個鍵維護一個 使用計數器 。使用計數最小的鍵是最久未使用的鍵。
當一個鍵首次插入到緩存中時，它的使用計數器被設置為 1 (由于 put 操作)。對緩存中的鍵執行 get 或 put 操作，使用計數器的值將會遞增。
你可以為這兩種操作設計時間復雜度為 O(1) 的實現嗎？
// 緩存的節點信息
struct Node {int key, val, freq;Node(int _key,int _val,int _freq): key(_key), val(_val), freq(_freq){}
};
class LFUCache {int minfreq, capacity;unordered_map<int, list<Node>::iterator> key_table;unordered_map<int, list<Node>> freq_table;
public:LFUCache(int _capacity) {minfreq = 0;capacity = _capacity;key_table.clear();freq_table.clear();}int get(int key) {if (capacity == 0) return -1;auto it = key_table.find(key);if (it == key_table.end()) return -1;list<Node>::iterator node = it -> second;int val = node -> val, freq = node -> freq;freq_table[freq].erase(node);// 如果當前鏈表為空，我們需要在哈希表中刪除，且更新minFreqif (freq_table[freq].size() == 0) {freq_table.erase(freq);if (minfreq == freq) minfreq += 1;}// 插入到 freq + 1 中freq_table[freq + 1].push_front(Node(key, val, freq + 1));key_table[key] = freq_table[freq + 1].begin();return val;}void put(int key, int value) {if (capacity == 0) return;auto it = key_table.find(key);if (it == key_table.end()) {// 緩存已滿，需要進行刪除操作if (key_table.size() == capacity) {// 通過 minFreq 拿到 freq_table[minFreq] 鏈表的末尾節點auto it2 = freq_table[minfreq].back();key_table.erase(it2.key);freq_table[minfreq].pop_back();if (freq_table[minfreq].size() == 0) {freq_table.erase(minfreq);}} freq_table[1].push_front(Node(key, value, 1));key_table[key] = freq_table[1].begin();minfreq = 1;} else {// 與 get 操作基本一致，除了需要更新緩存的值list<Node>::iterator node = it -> second;int freq = node -> freq;freq_table[freq].erase(node);if (freq_table[freq].size() == 0) {freq_table.erase(freq);if (minfreq == freq) minfreq += 1;}freq_table[freq + 1].push_front(Node(key, value, freq + 1));key_table[key] = freq_table[freq + 1].begin();}}
};合并鏈表
?
將兩個有序鏈表合并為一個新的有序鏈表并返回。新鏈表是通過拼接給定的兩個鏈表的所有節點組成的。?
示例：
輸入：1->2->4, 1->3->4
輸出：1->1->2->3->4->4
?
思路：鏈表歸并。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val = x; }* }*/
class Solution {public ListNode mergeTwoLists(ListNode l1, ListNode l2) {ListNode head=new ListNode(0);ListNode temp=head;while(l1!=null && l2!=null){if(l1.val>l2.val){temp.next=l2;l2=l2.next;}else{temp.next=l1;l1=l1.next; }temp=temp.next;}if(l1!=null){temp.next=l1;}else{temp.next=l2;}return head.next;}
}反轉鏈表
反轉一個單鏈表。
示例:
輸入: 1->2->3->4->5->NULL
輸出: 5->4->3->2->1->NULL
?
經典題不解釋，畫圖自己模擬記得清楚
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val = x; }* }*/
class Solution {public ListNode reverseList(ListNode head) {ListNode prev = null;ListNode curr = head;while (curr != null) {ListNode nextTemp = curr.next;curr.next = prev;prev = curr;curr = nextTemp;}return prev;}
}?反轉鏈表2
反轉從位置 m 到 n 的鏈表。請使用一趟掃描完成反轉。
說明:
1 ≤?m?≤?n?≤ 鏈表長度。
示例:
輸入: 1->2->3->4->5->NULL, m = 2, n = 4
輸出: 1->4->3->2->5->NULL
思路：反轉鏈表，只不過是反轉一部分，注意這一部分逆序之前做好記錄，方便逆序完后可以鏈接上鏈表的其他部分。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val = x; }* }*/
class Solution {public ListNode reverseBetween(ListNode head, int m, int n) {if (head == null) return null;ListNode cur = head, prev = null;while (m > 1) {prev = cur;cur = cur.next;m--;n--;}ListNode con = prev, tail = cur;ListNode third = null;while (n > 0) {third = cur.next;cur.next = prev;prev = cur;cur = third;n--;}if (con != null) {con.next = prev;} else {head = prev;}tail.next = cur;return head;}
}對鏈表排序
丟人，我就是按插入排序老老實實寫的啊。。。。
別人肯定map了hhh。
對鏈表進行插入排序。
插入排序的動畫演示如上。從第一個元素開始，該鏈表可以被認為已經部分排序（用黑色表示）。
每次迭代時，從輸入數據中移除一個元素（用紅色表示），并原地將其插入到已排好序的鏈表中。
?
插入排序算法：
插入排序是迭代的，每次只移動一個元素，直到所有元素可以形成一個有序的輸出列表。
每次迭代中，插入排序只從輸入數據中移除一個待排序的元素，找到它在序列中適當的位置，并將其插入。
重復直到所有輸入數據插入完為止。
?
示例 1：
輸入: 4->2->1->3
輸出: 1->2->3->4
示例?2：
輸入: -1->5->3->4->0
輸出: -1->0->3->4->5
思路：按插入排序思路寫就可以啦，只是注意鏈表操作，比數組麻煩很多。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val = x; }* }*/
class Solution {public ListNode insertionSortList(ListNode head) {ListNode ans=new ListNode(-1);ListNode temp=null;//要插入的地方ListNode key=null;//要插入的值while(head!=null){key=head;temp=ans;while(temp.next!=null && key.val>temp.next.val){temp=temp.next;}head=head.next;key.next=temp.next;temp.next=key;}return ans.next;}
}旋轉鏈表
給定一個鏈表，旋轉鏈表，將鏈表每個節點向右移動?k?個位置，其中?k?是非負數。
示例?1:
輸入: 1->2->3->4->5->NULL, k = 2
輸出: 4->5->1->2->3->NULL
解釋:
向右旋轉 1 步: 5->1->2->3->4->NULL
向右旋轉 2 步: 4->5->1->2->3->NULL
示例?2:
輸入: 0->1->2->NULL, k = 4
輸出: 2->0->1->NULL
解釋:
向右旋轉 1 步: 2->0->1->NULL
向右旋轉 2 步: 1->2->0->NULL
向右旋轉 3 步:?0->1->2->NULL
向右旋轉 4 步:?2->0->1->NULL
思路：找準斷點，直接調指針即可。
注意：長度可能超過鏈表長度，要取模。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val = x; }* }*/
class Solution {public ListNode rotateRight(ListNode head, int k) {if(head==null){return null;}int len=0;ListNode temp=head;while(temp!=null){temp=temp.next;len++;}k=k%len;ListNode node=head;ListNode fast=head;while(k-->0){fast=fast.next;}while(fast.next!=null){node=node.next;fast=fast.next;}fast.next=head;ListNode ans=node.next;node.next=null;return ans;}
}?數組實現棧
學習了改進，利用define typedef比上次寫的鏈表更容易改變功能，方便維護，代碼更健壯。
大佬別嫌棄，萌新總是很笨，用typedef都想不到。
#include<stdio.h>
#include<stdbool.h>
#define maxsize 10
typedef int datatype;
typedef struct stack
{datatype data[maxsize];int top;
}Stack;
Stack s;
void init()//初始化
{s.top=-1;
}
int Empty()//是否空
{if(s.top==-1)return 1;return 0;
}
int full()//是否滿
{if(s.top==maxsize-1)return 1;return 0;
}
void Push(datatype element)//入棧
{if(!full()){s.top++;s.data[s.top]=element;}else printf("棧滿\n");
}
void Pop()//出棧
{if(!Empty()) s.top--;else printf("棧空\n");
}
datatype Top()//取棧頂元素
{if(!Empty()) return s.data[s.top];printf("棧空\n");
}
void Destroy()//銷毀
{s.top=-1;
}測試不寫了。
?
鏈表實現棧
?
棧，是操作受限的線性表，只能在一端進行插入刪除。
其實就是帶尾指針的鏈表，尾插
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define Status int
#define SElemType int
//只在頭部進行插入和刪除(不帶頭結點)
typedef struct LNode
{SElemType data;struct LNode *next;
}LNode, *LinkList;typedef struct
{LNode *top;LNode *base;int length;
}LinkStack;Status InitStack(LinkStack &S)
{S.base = NULL;S.top = NULL;S.length = 0;return OK;
}Status GetTop(LinkStack S, SElemType &e)
{if(S.length == 0)return ERROR;e = S.top->data ;return OK;
}Status Push(LinkStack &S, SElemType e)
{LNode *newNode = (LNode *)malloc(sizeof(LNode));newNode->data = e;newNode->next = S.top;S.top = newNode;if(!S.base)S.base = newNode;++S.length;return OK;
}Status Pop(LinkStack &S, SElemType &e)
{LNode *p = S.top;if(S.length == 0)return ERROR;e = S.top->data;S.top = S.top->next;free(p);--S.length;return OK;
}void PrintStack(LinkStack S)
{LNode *p = S.top;printf("由棧頂到棧底：");while (p){printf("%d ",p->data);p = p->next;}printf("\n");
}int main(void)
{LinkStack LS;InitStack(LS);Push(LS,11);Push(LS,22);Push(LS,33);Push(LS,44);Push(LS,55);PrintStack(LS);SElemType e ;GetTop(LS , e);printf("棧頂元素是: %d\n",e);Pop(LS,e);PrintStack(LS);Pop(LS,e);PrintStack(LS);return 0;
}數組實現隊列
?
數組實現隊列結構：
相對棧結構要難搞一些，隊列的先進先出的，需要一個數組和三個變量，size記錄已經進來了多少個元素，不需要其它萌新看不懂的知識。
觸底反彈，頭尾追逐的感覺。
循環使用數組。
具體解釋一下觸底反彈：當我們的隊頭已經到了數組的底，我們就把對頭設為數組的第一個元素，對于隊尾也是一樣。實現了對數組的循環使用。
#include<stdio.h>
#include<stdbool.h>
#define maxsize 10
typedef int datatype;
typedef struct queue
{datatype arr[maxsize];int a,b,size;//頭、尾、數量
}queue;
queue s;
void init()//初始化
{s.a=0;s.b=0;s.size=0;
}
int Empty()//判空
{if(s.size==0)return 1;return 0;
}
int full()//判滿
{if(s.size==maxsize)return 1;return 0;
}
datatype peek()//查看隊頭
{if(s.size!=0)return s.arr[s.a];printf("queue is null\n");
}
datatype poll()//彈出隊頭
{int temp=s.a;if(s.size!=0){s.size--;s.a=s.a==maxsize-1? 0 :s.a+1;//觸底反彈return s.arr[temp];}printf("queue is null\n");
}
int push(datatype obj)//放入隊尾
{if(s.size!=maxsize){s.size++;s.arr[s.b]=obj;s.b=s.b==maxsize-1? 0 : s.b+1;//觸底反彈return 1;}printf("queue is full\n");return 0;
}
//測試
int main()
{int i;init();if(Empty())printf("null\n");for(i=0;i<20;i++)push(i);while(!Empty()){printf("%d\n",poll());}printf("%d",poll());
}
鏈表實現隊列
?
這次寫的還算正規，稍微壓縮了一下代碼，但是不影響閱讀
畫個圖幫助理解：
F->0->0->0<-R
第一個0不存數據?
?
#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
typedef int Elementype;//數據類型
//節點結構
typedef struct Node{Elementype Element;//數據域struct Node * Next;
}NODE,*PNODE;// 定義隊列結構體
typedef struct QNode {PNODE Front;//隊頭PNODE Rear;//隊尾
} Queue, *PQueue;void init(PQueue queue)//初始化
{//頭尾指向同一內存空間//頭結點，不存數據queue->Front = queue->Rear = (PNODE)malloc(sizeof(NODE));queue->Front->Next = NULL;//頭結點指針為空
}int isEmpty(PQueue queue)//判空·
{if(queue->Front == queue->Rear)return 1;return 0;
}void insert(PQueue queue,Elementype data)//入隊
{PNODE P = (PNODE)malloc(sizeof(NODE));//初始化P->Element = data;P->Next = NULL;queue->Rear->Next = P;//入隊queue->Rear = P;
}void delete(PQueue queue,int * val)//出隊，用val返回值
{if(isEmpty(queue))printf("隊空");else{PNODE P = queue->Front->Next;//前一元素*val = P->Element;//記錄值queue->Front->Next = P->Next;//出隊//注意一定要加上判斷，手動模擬一下就明白了if(P==queue->Rear)queue->Rear = queue->Front;free(P);//注意釋放P = NULL;}
}void destroy(PQueue queue)//釋放
{//從頭開始刪while(queue->Front != NULL)//起臨時指針作用，無需再用別的空間{queue->Rear = queue->Front->Next;free(queue->Front);queue->Front = queue->Rear;}
}
//測試
int main(void)
{int i;int e;Queue a;PQueue queue=&a;init(queue);for(i=0;i<10;i++)insert(queue,i);while(!isEmpty(queue))//遍歷{delete(queue,&e);printf("%d ",e);}if(isEmpty(queue))printf("1\n");delete(queue,&e);destroy(queue);
}雙棧的實現
利用棧底位置相對不變的特性，可以讓兩個順序棧共享一個空間。
具體實現方法大概有兩種：
一種是奇偶棧，就是所有下標為奇數的是一個棧，偶數是另一個棧。但是這樣一個棧的最大存儲就確定了，并沒有起到互補空缺的作用，我們實現了也就沒有太大意義。
還有一種就是，棧底分別設在數組的頭和尾。進棧往中間進就可以了。這樣，整個數組存滿了才會真的棧滿。
?
那我們直接開始代碼實現
?
首先定義結構體：
typedef struct
{int top[2], bot[2]; //棧頂和棧底指針int *V; //棧數組int m; //棧最大可容納元素個數
}DblStack;?
初始化雙棧s，長度為n：
void Init(DblStack &S,int n)
{S.m = n;S.V = new int [n+10];S.bot[0] = S.top[0] = -1;S.bot[1] = S.top[1] = S.m;
}判空：
int EmptyStack0(DblStack S)
{if(S.top[0]==-1)return 0;else return 1;
}int EmptyStack1(DblStack S)
{if(S.top[1]==S.m)return 0;else return 1;
}判滿：（沒有單獨判斷一個棧的，是判斷整個儲存空間還有沒有地方）
int FullStack(DblStack S)
{if(S.top[1]-S.top[0]==1)return 1;else return 0;
}進棧：
void Push0(DblStack &S,int e)
{if(S.top[1]-S.top[0]!=1){S.top[0]++;S.V[S.top[0]] = e;}
}
void Push1(DblStack &S,int e)
{if(S.top[1]-S.top[0] != 1){S.top[1]--;S.V[S.top[1]] = e;}
}出棧：
void Pop0(DblStack &S,int &e)
{if(S.top[0]!=-1){e = S.V[S.top[0]];S.top[0]--;}
}
void Pop1(DblStack &S,int &e)
{if(S.top[1]!=S.m){e = S.V[S.top[1]];S.top[1]++;}
}?棧/隊列 互相模擬實現
?
用兩個棧來實現一個隊列，完成隊列的Push和Pop操作。 隊列中的元素為int類型。
思路：大概這么想：用一個輔助棧把進第一個棧的元素倒一下就好了。
比如進棧1，2，3，4，5
第一個棧：
5
4
3
2
1
然后倒到第二個棧里
1
2
3
4
5
再倒出來，順序為1，2，3，4，5
實現隊列
然后要注意的事情：
1）棧2非空不能往里面倒數，順序就錯了。棧2沒數再從棧1倒。
2）棧1要倒就一次倒完，不倒完的話，進新數也會循序不對。
import java.util.Stack;public class Solution {Stack<Integer> stack1 = new Stack<Integer>();Stack<Integer> stack2 = new Stack<Integer>();public void push(int node) {stack1.push(node);}public int pop() {if(stack1.empty()&&stack2.empty()){throw new RuntimeException("Queue is empty!");}if(stack2.empty()){while(!stack1.empty()){stack2.push(stack1.pop());}}return stack2.pop();}
}?
用兩個隊列實現棧，要求同上：
這其實意義不是很大，有些數據結構書上甚至說兩個隊列不能實現棧。
其實是可以的，只是時間復雜度較高，一個彈出操作時間為O(N)。
思路：兩個隊列，編號為1和2.
進棧操作：進1號隊列
出棧操作：把1號隊列全弄到2號隊列里，剩最后一個別壓入，而是返回。
最后還得把1和2號換一下，因為現在是2號有數，1號空。
?
僅僅有思考價值，不實用。
比如壓入1，2，3
隊列1：1，2，3
隊列2：空
依次彈出1，2，3：
隊列1里的23進入2號，3彈出
隊列1：空
隊列2：2，3
?
隊列2中3壓入1號，2彈出
隊列1：3
隊列2：空
?
隊列1中只有一個元素，彈出。
?
上代碼：
public class TwoQueueImplStack {Queue<Integer> queue1 = new ArrayDeque<Integer>();Queue<Integer> queue2 = new ArrayDeque<Integer>();
//壓入public void push(Integer element){//都為空，優先1if(queue1.isEmpty() && queue2.isEmpty()){queue1.add(element);return;}//1為空，2有數據，放入2if(queue1.isEmpty()){queue2.add(element);return;}//2為空，1有數據，放入1if(queue2.isEmpty()){queue1.add(element);return;}}
//彈出public Integer pop(){//兩個都空，異常if(queue1.isEmpty() && queue2.isEmpty()){try{throw new Exception("satck is empty!");}catch(Exception e){e.printStackTrace();}} //1空，2有數據，將2中的數據依次放入1，最后一個元素彈出if(queue1.isEmpty()){while(queue2.size() > 1){queue1.add(queue2.poll());}return queue2.poll();}//2空，1有數據，將1中的數據依次放入2，最后一個元素彈出if(queue2.isEmpty()){while(queue1.size() > 1){queue2.add(queue1.poll());}return queue1.poll();}return (Integer)null;}
//測試public static void main(String[] args) {TwoQueueImplStack qs = new TwoQueueImplStack();qs.push(2);qs.push(4);qs.push(7);qs.push(5);System.out.println(qs.pop());System.out.println(qs.pop());qs.push(1);System.out.println(qs.pop());}
}
?
棧的排序
? 一個棧中元素的類型為整型，現在想將該棧從頂到底按從大到小的順序排序，只許申請一個棧。除此之外，可以申請新的變量，但是不能申請額外的數據結構，如何完成排序？
思路：
? ? 將要排序的棧記為stack,申請的輔助棧記為help.在stack上執行pop操作，彈出的元素記為cru.
? ? ? 如果cru小于或等于help的棧頂元素，則將cru直接壓入help.
? ? ? 如果cru大于help的棧頂元素，則將help的元素逐一彈出，逐一壓入stack,直到cru小于或等于help的棧頂元素，再將cru壓入help.
一直執行以上操作，直到stack中的全部元素壓入到help，最后將heip中的所有元素逐一壓入stack,完成排序。
?
其實和維持單調棧的思路挺像的，只是彈出后沒有丟棄，接著放。
和基礎排序也挺像。
?
import java.util.Stack;
public class a{public static void sortStackByStack(Stack<Integer> stack){Stack<Integer> help=new Stack<Integer>();while(!stack.isEmpty()){int cru=stack.pop();while(!help.isEmpty()&&help.peek()<cru){stack.push(help.pop());}help.push(cru);}while (!help.isEmpty()) {stack.push(help.pop()); }}
}棧——括號匹配
棧的應用，括號匹配。
經典做法是，遇左括號壓入，遇右括號判斷，和棧頂配對就繼續，不配對或者棧空就錯了。最后判斷是否為空。
代碼有些麻煩。
?
我是遇左括號壓對應的右括號，最后判斷代碼就會很簡單：相等即可。
class Solution {
public:bool isValid(string s) {int len=s.size();stack<char> st;for(int i=0;i<len;i++){if(s[i]=='(')st.push(')');else if(s[i]=='[')st.push(']');else if(s[i]=='{')st.push('}');else if(st.empty())return false;else if(st.top()!=s[i])return false;else st.pop();}return st.empty();}
};棧——表達式求值?
今天把表達式求值給搞定吧。
?
問題：給你個表達式，有加減乘除和小括號，讓算出結果。
我們假定計算式是正確的，并且不會出現除數為0等錯誤。
py大法好啊，在保證可讀性的前提下能壓到一共就三十多行代碼。
其實能壓到不到三十行，但是代碼就不好看了。。。。
計算函數：
def getvalue(a, b, op):if op == "+":return a+belif op == "-":return a-belif op == "*":return a*belse:return a/b?
出棧一個運算符，兩個數值，計算，將結果入data用于之后計算
def process(data, opt):operator = opt.pop()num2 = data.pop()num1 = data.pop()data.append(getvalue(num1, num2, operator))比較符號優先級：
乘除運算優先級比加減高。
op1優先級比op2高返回True，否則返回False
def compare(op1, op2):return op1 in ["*","/"] and op2 in ["+","-"]主函數：
基本思路：
處理每個數字為一個整數，處理每一項為一個單獨的數字，把括號內處理為一個單獨的數字。
把式子處理為只有整數、加減的式子再最后計算。
def calculate(s):data = []#數據棧opt = []#操作符棧i = 0 #表達式遍歷的索引while i < len(s):if s[i].isdigit(): # 數字,入棧datastart = iwhile i+1 < len(s) and s[i + 1].isdigit():i += 1data.append(int(s[start: i + 1])) # i為最后一個數字字符的位置elif s[i] == ")": # 右括號，opt出棧,data出棧并計算，結果入data，直到左括號while opt[-1] != "(":process(data,opt)#優先級高的一定先彈出opt.pop() # 出棧的一定是左括號elif not opt or opt[-1] == "(":opt.append(s[i])#棧空，或棧頂為左括號，入optelif s[i]=="(" or compare(s[i],opt[-1]):opt.append(s[i])#左括號或比棧頂優先級高，入else: #優先級不比棧頂高，opt出棧同時data出棧并計算，計算結果入datawhile opt and not compare(s[i], opt[-1]):if opt[-1] == "(":break #遇到左括號，停止計算process(data, opt)opt.append(s[i])i += 1 #索引后移while opt:process(data, opt)print(data.pop())借漢諾塔理解棧與遞歸
我們先說，在一個函數中，調用另一個函數。
首先，要意識到，函數中的代碼和平常所寫代碼一樣，也都是要執行完的，只有執行完代碼，或者遇到return，才會停止。
那么，我們在函數中調用函數，執行完了，就會重新回到本函數中，繼續向下執行，直到結束。
在執行其它函數時，本函數相當于中斷了，不執行了。那我們重新回來的時候，要從剛才暫停的地方開始，繼續執行，這期間，所有現場信息都要原封不動，就相當于時間暫停了一樣，什么都不能改變，這樣才能做到程序的準確。
所以，通常，在執行另一個函數之前，電腦會將現場信息壓入一個系統棧，為被調用的函數分配存儲區，然后開始執行被調函數。執行完畢后，保存計算結果，釋放被調函數的空間，按照被調函數里保存的返回地址，返回到原函數。
那什么是遞歸函數呢？
就是多個函數嵌套調用。不同的是，這些函數是同一個函數，只是參數可能不同，甚至參數也一樣，只是存儲空間不同。
每一層遞歸所需信息構成一個棧，每一塊內存儲著所有實在參數，所有局部變量，上一層的返回地址，等等一切現場信息。每執行完就彈出。
遞歸函數有著廣泛應用，主要適合可以把自身分化成一樣的子問題的問題。比如漢諾塔。
?
漢諾塔：漢諾塔（又稱河內塔）問題是源于印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。并且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次只能移動一個圓盤。
思路：函數（n,a,b,c)含義是把n個盤子從a柱子搬到c柱子的方法
一個盤子，直接搬過去。
多個盤子，我們把n-1個盤子都移動到另一個柱子上，把最大的搬過去然后把剩下的搬過去。
?
def hanoi(n, a, b, c):if n == 1:print(a, '-->', c)else:hanoi(n - 1, a, c, b)print(a, '-->', c)hanoi(n - 1, b, a, c)
# 調用
hanoi(3, 'A', 'B', 'C')結果：
A --> C
A --> B
C --> B
A --> C
B --> A
B --> C
A --> C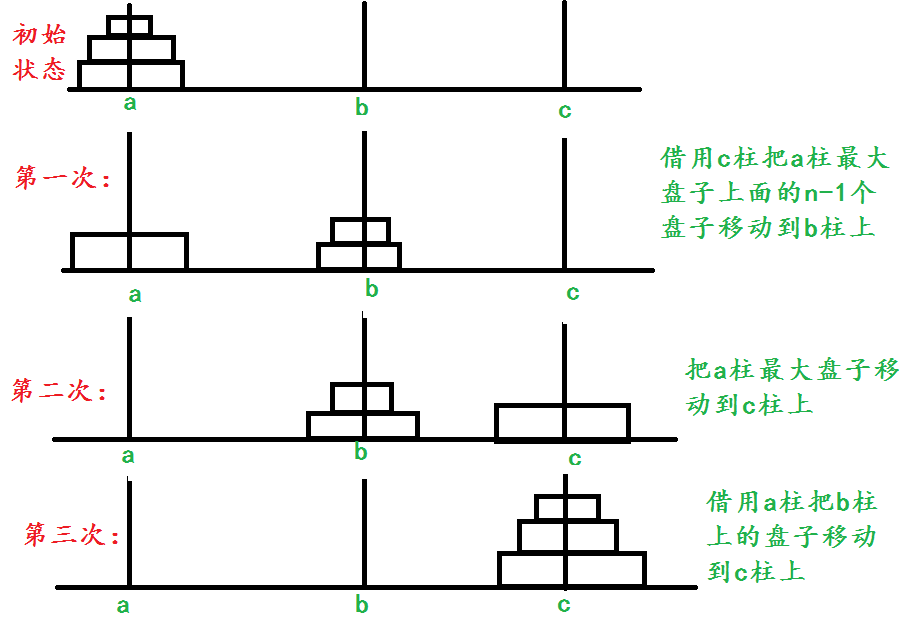
我們的棧：
第一次：
我們把hanoi(3, 'A', 'B', 'C')存了起來，調用了hanoi(3-1, 'A', 'C', 'B'),現在棧里壓入了3, 'A', 'B', 'C'，還有函數執行到的位置等現場信息。然后執行hanoi(3-1, 'A', 'C', 'B')，發現要調用hanoi(3-1-1, 'A', 'B', 'C')，我們又把3-1, 'A', 'C', 'B'等信息壓入了棧，現在棧是這樣的：
棧頭
2, 'A', 'C', 'B'
3, 'A', 'B', 'C'
棧尾
?
然后執行hanoi(3-1-1, 'A', 'B', 'C')，發現n=1了，打印了第一條A --> C，然后釋放掉了hanoi(3-1-1, 'A', 'B', 'C')的空間，并通過記錄的返址回到了hanoi(3-1, 'A', 'C', 'B')，然后執行打印語句A --> B，然后發現要調用hanoi(3-1-1, 'C', 'A', 'B')，此時棧又成了：
2, 'A', 'C', 'B'
3, 'A', 'B', 'C'
調用hanoi(1, 'A', 'C', 'B')發現可以直接打印，C --> B。
然后我們又回到了2, 'A', 'C', 'B'這里。發現整個函數執行完了，那就彈出吧。這時棧是這樣的：
3, 'A', 'B', 'C'
只有這一個。
我們繼續執行這個函數的代碼，發現
def hanoi(n, a, b, c):
? ? if n == 1:
? ? ? ? print(a, '-->', c)
? ? else:
? ? ? ? hanoi(n - 1, a, c, b)//執行到了這里
? ? ? ? print(a, '-->', c)
? ? ? ? hanoi(n - 1, b, a, c)
?
那我們就繼續執行，發現要打印A --> C
然后繼續，發現要調用? ? ? ? hanoi(n - 1, b, a, c)，那我們繼續把現場信息壓棧，繼續執行就好了。
?
遞歸就是把大問題分解成小問題進而求解。
具體執行就是通過系統的棧來實現返回原函數的功能。
?
轉存失敗重新上傳取消?
?
多色漢諾塔問題：
?
奇數號圓盤著藍色，偶數號圓盤著紅色，如圖所示。現要求將塔座A 上的這一疊圓盤移到塔座B 上，并仍按同樣順序疊置。在移動圓盤時應遵守以下移動規則：
規則(1)：每次只能移動1 個圓盤；
規則(2)：任何時刻都不允許將較大的圓盤壓在較小的圓盤之上；
規則(3)：任何時刻都不允許將同色圓盤疊在一起；
?
其實雙色的漢諾塔就是和無色的漢諾塔算法類似，通過推理可知，無色漢諾塔的移動規則在雙色漢諾塔這里的移動規則并沒有違反。
這里說明第一種就可以了：Hanoi（n-1，A,C,B）;
在移動過程中，塔座上的最低圓盤的編號與n-1具有相同奇偶性，塔座b上的最低圓盤的編號與n-1具有不相同的奇偶性，從而塔座上的最低圓盤的編號與n具有相同的奇偶性，塔座上c最低圓盤的編號與n具有不同的奇偶性；
?
所以把打印操作換成兩個打印即可
?
總：因為遞歸可能會有重復子問題的出現。
就算寫的很好，無重復子問題，也會因為來回調用、返回函數，而速度較慢。所以，有能力的可以改為迭代或動態規劃等方法。
?
單調棧
通過使用棧這個簡單的結構，我們可以巧妙地降低一些問題的時間復雜度。
單調棧性質：
1、若是單調遞增棧，則從棧頂到棧底的元素是嚴格遞增的。若是單調遞減棧，則從棧頂到棧底的元素是嚴格遞減的。
2、越靠近棧頂的元素越后進棧。（顯而易見）
本文介紹單調棧用法
通過一道題來說明。
POJ2559
1. 題目大意：鏈接
給出一個柱形統計圖(histogram), 它的每個項目的寬度是1， 高度和具體問題有關。 現在編程求出在這個柱形圖中的最大面積的長方形。
7 2 1 4 5 1 3 37表示柱形圖有7個數據，分別是 2 1 4 5 1 3 3， 對應的柱形圖如下，最后求出來的面積最大的圖如右圖所示。
做法1：枚舉每個起點和終點，矩形面積就是長*最小高度。O(N^3)
做法2：區間最小值優化。O(N^2)
做法3：以每一個下標為中心向兩邊擴，遇到更短的就停，這樣我們可以確定以每一個下標高度為最高的矩形。O(N^2)
單調棧：維護一個單調遞增棧，所有元素各進棧和出棧一次即可。每個元素出棧的時候更新最大的矩形面積。
過程：
1）判斷當前元素小于棧頂
2）條件滿足，就可以更新棧頂元素的最大長度了，并且把棧頂彈出
3）繼續執行（1），直到條件不滿足。
?
重要結論：
1）棧頂下面一個元素一定是，棧頂左邊第一個比棧頂小的元素
2）當前元素一定是，右邊第一個比棧頂小的元素。
為什么呢？
比如這是個棧
，
1）如果右邊存在距離更近的比1號小的數，1號早已經彈出了。
2）如果左邊有距離更近的比1號小的數，
? ? ? ? ? ? ? ? 如果它比2號小，它會把2號彈出，自己成為2號
? ? ? ? ? ? ? ? ?如果它比2號大，它不會彈出2號，但是它會壓棧，變成2號，原來的2號成為3號。
所以不管怎么說，這個邏輯是正確的。
最后放代碼并講解
?
下面看一道難一些的題
LeetCode 85 Maximal Rectangle
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 6.二三行后面那六個1
?
給定一個由二進制組成的矩陣map，找到僅僅包含1的最大矩形，并返回其面積。
這道題是一行一行的做。對每一行都求出每個元素對應的高度，這個高度就是對應的連續1的長度，然后對每一行都更新一次最大矩形面積。
連續1長度也很好更新，本個元素是0，長度就是0，本個元素是1，那就加上之前的。
具體思路代碼中講解。
import java.util.Stack;public class MaximalRectangle {public static int maxRecSize(int[][] map) {if (map == null || map.length == 0 || map[0].length == 0) {return 0;}int maxArea = 0;int[] height = new int[map[0].length];for (int i = 0; i < map.length; i++) {for (int j = 0; j < map[0].length; j++) {height[j] = map[i][j] == 0 ? 0 : height[j] + 1;//0長度為0，1長度為前面+1}maxArea = Math.max(maxRecFromBottom(height), maxArea);//調用第一題的思想}return maxArea;}//第一題思路public static int maxRecFromBottom(int[] height) {if (height == null || height.length == 0) {return 0;}int maxArea = 0;Stack<Integer> stack = new Stack<Integer>();for (int i = 0; i < height.length; i++) {//棧非空并且棧頂大while (!stack.isEmpty() && height[i] <= height[stack.peek()]) {int j = stack.pop();//彈出int k = stack.isEmpty() ? -1 : stack.peek();int curArea = (i - k - 1) * height[j];//計算最大maxArea = Math.max(maxArea, curArea);//更新總體最大}stack.push(i);//直到棧頂小，壓入新元素}//最后棧非空，右邊沒有更小元素使它們彈出while (!stack.isEmpty()) {int j = stack.pop();int k = stack.isEmpty() ? -1 : stack.peek();int curArea = (height.length - k - 1) * height[j];maxArea = Math.max(maxArea, curArea);}return maxArea;}public static void main(String[] args) {int[][] map = { { 1, 0, 1, 1 }, { 1, 1, 1, 1 }, { 1, 1, 1, 0 }, };System.out.println(maxRecSize(map));}}?
雙端單調隊列
?
這次介紹一種新的數據結構：雙端隊列：雙端隊列是指允許兩端都可以進行入隊和出隊操作的隊列，其元素的邏輯結構仍是線性結構。將隊列的兩端分別稱為前端和后端，兩端都可以入隊和出隊。
堆棧、隊列和優先隊列都可以采用雙端隊列來實現
本文介紹單調雙端隊列的原理及應用。
單調隊列，顧名思義，就是一個元素單調的隊列，那么就能保證隊首的元素是最小（最大）的，從而滿足最優性問題的需求。
給定一個長度為n的數列，一個k，求所有的min(ai,ai+1.....ai+k-1),i=0,1,....n-k
通俗一點說就是一個長度固定的滑動的窗口，求每個窗口內的最小值。
你當然可以暴力求解，依次遍歷每個窗口.
介紹單調隊列用法：我們維護一個單調隊列
單調隊列呢，以單調遞增序列為例：
1、如果隊列的長度一定，先判斷隊首元素是否在規定范圍內，如果超范圍則增長隊首。
2、每次加入元素時和隊尾比較，如果當前元素小于隊尾且隊列非空，則減小尾指針，隊尾元素依次出隊，直到滿足隊列的調性為止
?
我們說算法的優化就是重復計算過程的去除。
按窗口一次次遍歷就是重復計算。最值信息沒有利用好。
我們為什么可以這么維護？
首先，遍歷到的元素肯定在隊列元素之后。
其次，如果當前元素更小的話。
頭部的值比當前元素大，頭部還比當前元素先過期。所以以后計算再也不會用到它了。我們可以放心的去掉它。
下面給出代碼和解釋
int n,k;//長度為n的數列，窗口為k
int a[MAX_N];//數列
int b[MAX_N];//存放
int deq[MAX_N]//模擬隊列void solve()
{int s = 0,t = 0;//頭和尾for(int i=0;i<n;i++){//不滿足單調,尾就彈出while(s<t && a[deq[t-1]]>=a[i])t--;//直到滿足，放入deq[t++]=i;//計算窗口最大值if(i-k+1>=0)b[i-k+1]=a[deq[s];//判斷頭過期彈出if(deq[s]==i-k+1)s++;}
}基本入門就到這里。
?單調隊列優化的背包問題
對于背包問題，經典的背包九講已經講的很明白了，本來就不打算寫這方面問題了。
但是吧。
我發現，那個最出名的九講竟然沒寫隊列優化的背包。。。。
那我必須寫一下咯嘿嘿，這么好的思想。
?
我們回顧一下背包問題吧。
?
01背包問題?
題目?
有N件物品和一個容量為V的背包。第i件物品的費用是c[i]，價值是w[i]。求解將哪些物品裝入背包可使這些物品的費用總和不超過背包容量，且價值總和最大。?
這是最基礎的背包問題，特點是：每種物品僅有一件，可以選擇放或不放。?
f[i][v]表示前i件物品恰放入一個容量為v的背包可以獲得的最大價值。則其狀態轉移方程便是：
f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}。?
就是說，對于本物品，我們選擇拿或不拿
比如費用是3.
相關圖解：
我們求表格中黃色部分，只和兩個黑色部分有關
拿了，背包容量減少，我們價值加上減少后最大價值。
不拿，最大價值等于沒有這件物品，背包不變，的最大價值。
完全背包問題?
題目?
有N種物品和一個容量為V的背包，每種物品都有無限件可用。第i種物品的費用是c[i]，價值是w[i]。求解將哪些物品裝入背包可使這些物品的費用總和不超過背包容量，且價值總和最大。?
基本思路?
這個問題非常類似于01背包問題，所不同的是每種物品有無限件。
f[i][v]=max{f[i-1][v],f[i][v-c[i]]+w[i]}
圖解：
因為我們拿了本物品還可以繼續拿無限件，對于當前物品，無論之前拿沒拿，還可以繼續拿，所以是f[i][v-c[i]]+w[i]
?
換一個角度說明這個問題為什么可以f[i][v-c[i]]+w[i]，也就是同一排。
其實是這樣的，我們對于黃色部分，也就是當前物品，有很多種選擇，可以拿一個，兩個。。。一直到背包容量不夠了。
也就是說，可以不拿，也就是J1，可以拿一個，也就是G1+w[i]，也可以拿兩個，也就是D1+2w[i]，拿三個，A1+3w[i]。
但是我們看G2，G2其實已經是之前的最大了：A1+2w[i]，D1+w[i]，G1他們中最大的，對么？
既然G2是他們中最大的。
我們怎么求J2？
是不是只要求G2+w[i]和J1的最大值就好了。
因為G2把剩下的情況都保存好了。
?
多重背包問題?
題目?
有N種物品和一個容量為V的背包。第i種物品最多有n[i]件可用，每件費用是c[i]，價值是w[i]。求解將哪些物品裝入背包可使這些物品的費用總和不超過背包容量，且價值總和最大。?
?
和之前的完全背包不同，這次，每件物品有最多拿n[i]件的限制。
思路一：我們可以把物品全都看成01背包：比如第i件，我們把它拆成n[i]件一樣的單獨物品即可。
思路二：思路一時間復雜度太高。利用二進制思路：一個n位二進制，能表示2^n種狀態，如果這些狀態就是拿了多少物品，我們可以把每一位代表的數都拿出來，比如n[i]=16，我們把它拆成1，2，4，8，1，每一堆物品看成一個單獨物品。
為什么最后有個一？因為從0到16有十七種狀態，四位不足以表示。我們最后補上第五位1.
把拆出來的物品按01背包做即可。
思路三：我們可以利用單調隊列：
https://blog.csdn.net/hebtu666/article/details/82720880
再回想完全背包：為什么可以那么做？因為每件物品能拿無限件。所以可以。而多重背包因為有了最多拿多少的限制，我們就不敢直接從G2中拿數，因為G2可能是拿滿了本物品以后才達到的狀態?。
比如n[i]=2，如果G2的狀態是2w[i]，拿了兩個2物品達到最大值，我們的J2就不能再拿本物品了。
如何解決這個問題？就是我給的網址中的，雙端單調隊列
利用窗口最大值的思想。
大家想想怎么實現再看下文。
?
發現問題了嗎？
我們求出J2以后，按原來的做法，是該求K2的，但是K2所需要的信息和J2完全不同，紅色才是K2可能需要的信息。
所以我們以物品重量為差，先把黑色系列推出來，再推紅色系列，依此類推。
這個例子就是推三次，每組各元素之間差3.
這樣就不會出現構造一堆單調隊列的尷尬情況了。
在代碼中繼續詳細解釋：
//輸入
int n;
int W;
int w[MAX_N];
int v[MAX_N];
int m[MAX_N];?
int dp[MAX_N+1];//壓空間，本知識參考https://blog.csdn.net/hebtu666/article/details/79964233
int deq[MAX_N+1];//雙端隊列，保存下標
int deqv[MAX_N+1];//雙端隊列，保存值隊列存的就是所有上一行能取到的范圍，比如對于J2，隊列里存的就是G1-w[i]，D1-2w[i]，A1-3w[i]等等合法情況。（為了操作方便都是j，利用差實現最終的運算）
他們之中最大的就是隊頭，加上最多存儲個數就好。
?
?
?
void solve()
{for(int i=0;i<n;i++)//參考過那個網址第二題應該懂{for(int a=0;a<w[i];a++)//把每個分組都打一遍{int s=0;//初始化雙端隊列頭尾int t=0;for(int j=0;j*w[i]+a<=W;j++)//每組第j個元素{int val=dp[j*w[i]+a]-j*v[i];while(s<t && deqv[t-1]<=val)//直到不改變單調性t--;deq[t]=j;deqv[t]=val;t++;//利用隊頭求出dpdp[j*w[i]+a]=deqv[s]+j*v[i];if(deq[s]==j-m[i])s++;//檢查過期}}}
}?串的定長表示
思想和代碼都不難，和線性表也差不多，串本來就是數據受限的線性表。
串連接：
?
#include <stdio.h>
#include <string.h>
//串的定長順序存儲表示
#define MAXSTRLEN 255 //用戶可在255以內定義最大串長
typedef unsigned char SString[MAXSTRLEN + 1]; //0號單元存放串的長度int Concat(SString *T,SString S1,SString S2)//用T返回S1和S2聯接而成的新串。若未截斷返回1，若截斷返回0
{int i = 1,j,uncut = 0;if(S1[0] + S2[0] <= MAXSTRLEN) //未截斷{for (i = 1; i <= S1[0]; i++)//賦值時等號不可丟(*T)[i] = S1[i];for (j = 1; j <= S2[0]; j++)(*T)[S1[0]+j] = S2[j]; //(*T)[i+j] = S2[j](*T)[0] = S1[0] + S2[0];uncut = 1;}else if(S1[0] < MAXSTRLEN) //截斷{for (i = 1; i <= S1[0]; i++)//賦值時等號不可丟(*T)[i] = S1[i];for (j = S1[0] + 1; j <= MAXSTRLEN; j++){(*T)[j] = S2[j - S1[0] ];(*T)[0] = MAXSTRLEN;uncut = 0;}}else{for (i = 0; i <= MAXSTRLEN; i++)(*T)[i] = S1[i];/*或者分開賦值，先賦值內容，再賦值長度for (i = 1; i <= MAXSTRLEN; i++)(*T)[i] = S1[i];(*T)[0] = MAXSTRLEN;*/uncut = 0;}return uncut;
}int SubString(SString *Sub,SString S,int pos,int len)//用Sub返回串S的第pos個字符起長度為len的子串//其中，1 ≤ pos ≤ StrLength(S)且0 ≤ len ≤ StrLength(S) - pos + 1(從pos開始到最后有多少字符)//第1個字符的下標為1,因為第0個字符存放字符長度
{int i;if(pos < 1 || pos > S[0] || len < 0 || len > S[0] - pos + 1)return 0;for (i = 1; i <= len; i++){//S中的[pos,len]的元素 -> *Sub中的[1,len](*Sub)[i] = S[pos + i - 1];//下標運算符 > 尋址運算符的優先級}(*Sub)[0] = len;return 1;
}
void PrintStr(SString S)
{int i;for (i = 1; i <= S[0]; i++)printf("%c",S[i]);printf("\n");
}int main(void)
{/*定長順序存儲初始化和打印的方法SString s = {4,'a','b','c','d'};int i;//s = "abc"; //不可直接賦值for (i = 1; i <= s[0]; i++)printf("%c",s[i]);*/SString s1 = {4,'a','b','c','d'};SString s2 = {4,'e','f','g','h'},s3;SString T,Sub;int i;for (i = 1; i <= 255; i++){s3[i] = 'a';if(i >= 248)s3[i] = 'K';}s3[0] = 255;SubString(&Sub,s3,247,8);PrintStr(Sub);return 0;
}串的堆分配實現
?
今天，線性結構基本就這樣了，以后（至少是最近）就很少寫線性基礎結構的實現了。
串的類型定義
typedef struct
{char *str;int length;
}HeapString;
初始化串
InitString(HeapString *S)
{S->length=0;S->str='\0';
}長度
int StrEmpty(HeapString S)
/*判斷串是否為空，串為空返回1，否則返回0*/
{if(S.length==0) ? ? ? ? /*判斷串的長度是否等于0*/return 1; ? ? ? ? ? /*當串為空時，返回1；否則返回0*/elsereturn 0;
}
int StrLength(HeapString S)
/*求串的長度操作*/
{return S.length;
}
串的賦值
void StrAssign(HeapString *S,char cstr[])
/*串的賦值操作*/
{int i=0,len;if(S->str)free(S->str);for(i=0;cstr[i]!='\0';i++); /*求cstr字符串的長度*/len=i;if(!i){S->str=NULL;S->length=0;}else{S->str=(char*)malloc((len+1)*sizeof(char));if(!S->str)exit(-1);for(i=0;i<len;i++)S->str[i]=cstr[i];S->length=len;}
}
串的復制
void StrAssign(HeapString *S,char cstr[])
/*串的賦值操作*/
{int i=0,len;if(S->str)free(S->str);for(i=0;cstr[i]!='\0';i++); /*求cstr字符串的長度*/len=i;if(!i){S->str=NULL;S->length=0;}else{S->str=(char*)malloc((len+1)*sizeof(char));if(!S->str)exit(-1);for(i=0;i<len;i++)S->str[i]=cstr[i];S->length=len;}
}
串的插入
int StrInsert(HeapString *S,int pos,HeapString T)
/*串的插入操作。在S中第pos個位置插入T分為三種情況*/
{int i;if(pos<0||pos-1>S->length) ? ? ?/*插入位置不正確，返回0*/{printf("插入位置不正確");return 0;}S->str=(char*)realloc(S->str,(S->length+T.length)*sizeof(char));if(!S->str){printf("內存分配失敗");exit(-1);}for(i=S->length-1;i>=pos-1;i--)S->str[i+T.length]=S->str[i];for(i=0;i<T.length;i++)S->str[pos+i-1]=T.str[i];S->length=S->length+T.length;return 1;
}
串的刪除
int StrDelete(HeapString *S,int pos,int len)
/*在串S中刪除pos開始的len個字符*/
{int i;char *p;if(pos<0||len<0||pos+len-1>S->length){printf("刪除位置不正確，參數len不合法");return 0;}p=(char*)malloc(S->length-len); ? ? ? ? ? ? /*p指向動態分配的內存單元*/if(!p)exit(-1);for(i=0;i<pos-1;i++) ? ? ? ? ? ? ? ? ? ? ? ?/*將串第pos位置之前的字符復制到p中*/p[i]=S->str[i];for(i=pos-1;i<S->length-len;i++) ? ? ? ? ? ? ? ?/*將串第pos+len位置以后的字符復制到p中*/p[i]=S->str[i+len];S->length=S->length-len; ? ? ? ? ? ? ? ? ? ?/*修改串的長度*/free(S->str); ? ? ? ? ? ? ? ? ? ? ? ? ? /*釋放原來的串S的內存空間*/S->str=p; ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? /*將串的str指向p字符串*/return 1;
}
串的比較
int StrCompare(HeapString S,HeapString T)
/*串的比較操作*/
{
int i;
for(i=0;i<S.length&&i<T.length;i++) /*比較兩個串中的字符*/if(S.str[i]!=T.str[i]) ? ? ? ? ?/*如果出現字符不同，則返回兩個字符的差值*/return (S.str[i]-T.str[i]);
return (S.length-T.length); ? ? ? ? ? ? /*如果比較完畢，返回兩個串的長度的差值*/
}
串的連接
int StrCat(HeapString *T,HeapString S)
/*將串S連接在串T的后面*/
{int i;T->str=(char*)realloc(T->str,(T->length+S.length)*sizeof(char));if(!T->str){printf("分配空間失敗");exit(-1);}else{for(i=T->length;i<T->length+S.length;i++) ? /*串S直接連接在T的末尾*/T->str[i]=S.str[i-T->length];T->length=T->length+S.length; ? ? ? ? ? /*修改串T的長度*/}return 1;
}
清空串
void StrClear(HeapString *S)
/*清空串，只需要將串的長度置為0即可*/
{S->str='\0';S->length=0;
}
銷毀串
void StrDestroy(HeapString *S)
{if(S->str)free(S->str);
}打印
void StrPrint(HeapString S)
{int i;for(i=0;i<S.length;i++){printf("%c",S.str[i]);}printf("\n");
}KMP
Kmp操作、原理、拓展
?
?
注：雖然我是一只菜，才大一。但我是想讓萌新們更容易的學會一些算法和思想，所以沒有什么專業詞語，用的都是比較直白地表達，大佬們可能覺得煩，但是真的對不會的人更有幫助啊。我本人也是菜，大一上學期寫的，直接拿過來了，也沒檢查，有什么錯誤大佬們趕緊告訴我
先上代碼，大佬們可以別看下面了，就當復習一下
package advanced_001;public class Code_KMP {public static int getIndexOf(String s, String m) {if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {return -1;}char[] str1 = s.toCharArray();char[] str2 = m.toCharArray();int i1 = 0;int i2 = 0;int[] next = getNextArray(str2);while (i1 < str1.length && i2 < str2.length) {if (str1[i1] == str2[i2]) {i1++;i2++;} else if (next[i2] == -1) {i1++;} else {i2 = next[i2];}}return i2 == str2.length ? i1 - i2 : -1;}public static int[] getNextArray(char[] ms) {if (ms.length == 1) {return new int[] { -1 };}int[] next = new int[ms.length];next[0] = -1;next[1] = 0;int i = 2;int cn = 0;while (i < next.length) {if (ms[i - 1] == ms[cn]) {next[i++] = ++cn;} else if (cn > 0) {cn = next[cn];} else {next[i++] = 0;}}return next;}public static void main(String[] args) {String str = "abcabcababaccc";String match = "ababa";System.out.println(getIndexOf(str, match));}}
?
問題：給定主串S和子串 T，如果在主串S中能夠找到子串 T，則匹配成功，返回第一個和子串 T 中第一個字符相等的字符在主串S中的序號；否則，稱匹配失敗，返回 0。
?
一、引子
原始算法：以主串中每一個位置為開頭，與子串第一個元素匹配，若相同，下一個位置和子串下一個位置匹配，如果子串元素全部匹配成功，則匹配成功，找到位置。
非常傻白甜，很明顯時間復雜度最差為o(len(s)*len(t))。效率很低，大佬請忽略：
?
引出KMP算法，概念如下：KMP算法是一種改進的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同時發現，因此人們稱它為克努特——莫里斯——普拉特操作（簡稱KMP算法）。KMP算法的關鍵是利用匹配失敗后的信息，盡量減少模式串與主串的匹配次數以達到快速匹配的目的。具體實現就是實現一個next()函數，函數本身包含了模式串的局部匹配信息。時間復雜度O(m+n)。（摘自百度百科）
?
?
其實就是說，人家kmp算法時間復雜度o(len(s)+len(t))，非常快了，畢竟你不遍歷一遍這倆字符串，怎么可能匹配出來呢？我不信還有時間復雜度更低的算法，包括優化也是常數范圍的優化，時間已經非常優秀了
二、分析總結
分析：首先，我們要搞明白，原始的算法為啥這么慢呢？因為它在一遍一遍的遍歷s和t，做了很多重復工作，浪費了一些我們本該知道的信息。大大降低了效率。
比如t長度為10，s匹配到位置5，如果t一直匹配到了t[8],到[9]才匹配錯誤，那s已經匹配到了位置14，下一步怎么做呢？接著從位置6開始，和t[0]開始匹配，而s位置6和t[0]甚至后面很大一部分信息我們其實都遍歷過，都知道了，原始算法卻還要重復匹配這些位置。所以效率極低。
(其實很多算法都是對一般方法中的重復運算、操作做了優化，當我們寫出暴力遞歸后，應分析出我們做了哪些重復運算，然后優化。具體優化思路我會在以后寫出來。當我們可以用少量的空間就能減少大量的時間時，何樂而不為呢？)
扯遠了，下面開始進入kmp正題。
三、基本操作
首先扯基本操作：
next數組概念：一個字符串中最長的相同前后綴的長度,加一。可能表達的不太好啊，舉例說明：abcabcabc
所以next[1]一直到next[9]計算的是’a’,’ab’,’abc’,’abca’,’abcab’直到’abcabcabc’的相同的最長前綴和最長后綴，加一
注意，所謂前綴，不能包含最后一個字符，而后綴，也不能包含第一個字符，如果包含，那所有的next都成了字符串長度，也就沒意義了。
比如’a’,最長前后綴長度為0，原因上面剛說了，不包含。
“abca”最長前后綴長度為1，即第一個和最后一個。
“abcab”最長前后綴長度為2,即ab
“abcabc”最長前后綴長度為3,即abc
“abcabca”最長前后綴長度為4,即abca
“abcabcabc”最長前后綴長度為6,即abcabc
萌新可以把next數組看成一個黑盒，我下面會寫怎么求，不過現在先繼續講主體思路。
(感覺next數組體現了一個挺重要的思想：預處理思想。當我們不能直接求解問題時，不妨先生成一個預處理的數組，用來記錄我們需要的一些信息。以后我會寫這方面的專題)
?
?
?
?
開始匹配了哦：假如主串從i位置開始和子串配，配到了i+j時配不下去了，按原來的方法，應該回到i+1，繼續配，而kmp算法是這樣的：
黑色部分就是配到目前為止，前面子串中的最長相同前后綴。匹配失敗以后，可以跳過我圈的那一部分開頭，從主串的第二塊黑色那里開始配了，這些開頭肯定配不出來，這就是kmp核心的思想，至于為什么敢跳，等會講，現在先說基本操作。
根據定義，主串第二塊黑部分和子串第一塊黑部分也一樣，所以直接從我劃線的地方往下配就好。
就這樣操作，直到最后或配出。
?
四、原理
原始的kmp操作就是這樣，下面講解原理，為什么能確定跳過的那一段開頭肯定配不出來呢？
還是再畫一個圖來配合講解吧。(要不然我怕表達不好唉。。好氣喲)
(懶，就是剛才的圖改了改）
咱們看普遍情況(注意，是普遍情況，任意跳過的開頭位置)，隨便一個咱們跳過的開頭，看看有沒有可能配出來呢？
豎線叫abc吧。
主串叫s，子串交t
請看ab線中間包含的t中的子串，它在t中是一個以t[0]為開頭，比黑塊更長的前綴。
請看ab線中間包含的s中的子串，它在s中是一個以b線前一個元素為結尾，比黑塊更長的后綴。
請回想黑塊定義：這是目前位置之前的子串中，最長的相同前后綴。
請再想一想我們當初為什么能配到這里呢？
?
這個位置之前，我們全都一樣，所以多長的后綴都是相等的。
其實就是，主數組后綴等于子數組后綴，而子數組前綴不等于子數組后綴，所以子數組前綴肯定不等與主數組后綴，也就是說，當前位置肯定配不出來
?
這是比最長相同前后綴更長的前后綴啊兄弟。。。所以肯定不相等，如果相等，最長相同前后綴至少也是它了啊，對么？這就是能跳過的原因，這輩子不可能在這里面配出來了哦。
主要操作和原理就這些了。。不知道解釋清楚沒。
下面解釋如何求解next數組：
?
當然，一個一個看也不是不可以，在子串很短的情況下算法總時間區別不大，但是。。各位有沒有一股似曾相識的感覺呢？計算next[x]還是要在t[0]-t[x-2]這個串里找最大相同前后綴啊。還是串匹配問題啊。看操作：
(一切為了code簡潔好操作),之后每個位置看看p[i-1]和p[next[i-1]]是不是相等，請回去看圖，也就是第一個黑塊后面那個元素和第二個黑塊最后那個元素，相等，next[i]就等于next[i-1]+1。(求b，看前一個元素的最長前后綴，前一個元素和a看是不是相等。)
若不等，繼續往前看，p[i-1]是不是等于p[next[next[i-1]]]，就這樣一直往前跳。其實現在一看，大家是不是感覺，和s與t匹配的時候kmp主體很像啊？只是反過來跳了嘛。。。原理也是基本一樣的，我就不解釋了，跳過的部分也不可能配出來，你們自己證吧，不想寫了。
?
五、復雜度分析
下面分析時間復雜度：
主體部分，在主串上的指針，兩種情況，要么配了頭一個就不對，就往后走了，這時用o(1)排除了一個位置。要么就是，配了n個位置以后配不對了，那不管next數組是多少，主串上的指針總會向后走n個位置的，所以每個位置還是o(1)，這樣看來，主串長度是len的話，時間復雜度就是o(len)啊。
再看next數組求解的操作，一樣的啊，最多就是子串的長度那么多唄。
所以總體時間復雜度o(m+n),原來是o(m*n)啊，向這位大神致敬，想出這么強的算法。
六、kmp拓展題目
（本來想放到樹專題講，但是kmp提供了很好的思路，故在本章講述kmp方法，在樹專題講一般思路）
輸入兩棵二叉樹A，B，判斷B是不是A的子結構。
Oj鏈接
https://www.nowcoder.com/practice/6e196c44c7004d15b1610b9afca8bd88?tpId=13&tqId=11170&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
先說一般思路，就一個一個試唄，先在A里找B的根，相等了接著往下配，全配上就行了。
需要注意的是，子結構的定義，好好理解，不要搞錯了，不太清楚定義的自己查資料。
?
下面說利用kmp解此題的思路
Kmp，解決字符串匹配問題，而此題是二叉樹匹配問題，所以一般思路是想把樹序列化，然后用kmp，但是我們有一個常識，一種遍歷不能確定唯一一顆樹，這是我們首先要解決的問題。
分析為什么一個序列不能確定呢？給你個序列建立二叉樹，比如1 2 3，先序吧（默認先左子樹），1是根沒問題，2就不一定了，可以是左子樹可以是右子樹，假如是左子樹，那三可放的位置更不確定，這就是原因，我們不知道左子樹是空，結束了，該建右子樹，還是說，填在左子樹。
怎么解決這個問題？
我請教了敬愛的老師這方法對不對，所以肯定沒有問題滴。
只要把空也表示出來就好了比如
再舉一例
在座的各位都是大佬，應該都懂吧。
(因為序列化和重建的方式一樣，知道左子樹什么時候為空，所以可以確定唯一一顆結構確定的樹)
AB樹序列化以后，用kmp字符串匹配就行啦
（當然要是為了過oj，就別秀kmp操作了，直接用系統函數，面試再自己寫）
?
?
?
整篇結束，code怎么整合，如何操作、kmp的優化，以及篇中提到的算法思想怎么養成以后可能會寫。
字數3170
?
初稿2017/12/20
?
?18/11/26添加網址和代碼：
https://blog.csdn.net/hebtu666/article/details/84553147
public class T1SubtreeEqualsT2 {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static boolean isSubtree(Node t1, Node t2) {String t1Str = serialByPre(t1);String t2Str = serialByPre(t2);return getIndexOf(t1Str, t2Str) != -1;}public static String serialByPre(Node head) {if (head == null) {return "#!";}String res = head.value + "!";res += serialByPre(head.left);res += serialByPre(head.right);return res;}// KMPpublic static int getIndexOf(String s, String m) {if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {return -1;}char[] ss = s.toCharArray();char[] ms = m.toCharArray();int[] nextArr = getNextArray(ms);int index = 0;int mi = 0;while (index < ss.length && mi < ms.length) {if (ss[index] == ms[mi]) {index++;mi++;} else if (nextArr[mi] == -1) {index++;} else {mi = nextArr[mi];}}return mi == ms.length ? index - mi : -1;}public static int[] getNextArray(char[] ms) {if (ms.length == 1) {return new int[] { -1 };}int[] nextArr = new int[ms.length];nextArr[0] = -1;nextArr[1] = 0;int pos = 2;int cn = 0;while (pos < nextArr.length) {if (ms[pos - 1] == ms[cn]) {nextArr[pos++] = ++cn;} else if (cn > 0) {cn = nextArr[cn];} else {nextArr[pos++] = 0;}}return nextArr;}public static void main(String[] args) {Node t1 = new Node(1);t1.left = new Node(2);t1.right = new Node(3);t1.left.left = new Node(4);t1.left.right = new Node(5);t1.right.left = new Node(6);t1.right.right = new Node(7);t1.left.left.right = new Node(8);t1.left.right.left = new Node(9);Node t2 = new Node(2);t2.left = new Node(4);t2.left.right = new Node(8);t2.right = new Node(5);t2.right.left = new Node(9);System.out.println(isSubtree(t1, t2));}}
?
Manacher
Manacher's Algorithm 馬拉車算法操作及原理?
package advanced_001;public class Code_Manacher {public static char[] manacherString(String str) {char[] charArr = str.toCharArray();char[] res = new char[str.length() * 2 + 1];int index = 0;for (int i = 0; i != res.length; i++) {res[i] = (i & 1) == 0 ? '#' : charArr[index++];}return res;}public static int maxLcpsLength(String str) {if (str == null || str.length() == 0) {return 0;}char[] charArr = manacherString(str);int[] pArr = new int[charArr.length];int C = -1;int R = -1;int max = Integer.MIN_VALUE;for (int i = 0; i != charArr.length; i++) {pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {if (charArr[i + pArr[i]] == charArr[i - pArr[i]])pArr[i]++;else {break;}}if (i + pArr[i] > R) {R = i + pArr[i];C = i;}max = Math.max(max, pArr[i]);}return max - 1;}public static void main(String[] args) {String str1 = "abc1234321ab";System.out.println(maxLcpsLength(str1));}}
問題：查找一個字符串的最長回文子串
首先敘述什么是回文子串：回文：就是對稱的字符串，或者說是正反一樣的
小問題一：請問，子串和子序列一樣么？請思考一下再往下看
?當然，不一樣。子序列可以不連續，子串必須連續。
舉個例子，”123”的子串包括1，2，3，12，23，123(一個字符串本身是自己的最長子串)，而它的子序列是任意選出元素組成，他的子序列有1，2，3，12，13，23，123，””,空其實也算，但是本文主要是想敘述回文，沒意義。
小問題二：長度為n的字符串有多少個子串？多少個子序列？
?子序列，每個元素都可以選或者不選，所以有2的n次方個子序列（包括空）
子串：以一位置開頭，有n個子串，以二位置開頭，有n-1個子串，以此類推，我們發現，這是一個等差數列，而等差序列求和，有n*(n+1)/2個子串(不包括空)。
(這里有一個思想需要注意，遇到等差數列求和，基本都是o(n^2)級別的)
一、分析枚舉的效率
好，我們來分析一下暴力枚舉的時間復雜度，上文已經提到過，一個字符串的所有子串，數量是o(n^2)級別，所以光是枚舉出所有情況時間就是o(n^2)，每一種情況，你要判斷他是不是回文的話，還需要o(n)，情況數和每種情況的時間，應該乘起來，也就是說，枚舉時間要o(n^3)，效率太低。
二、初步優化
思路：我們知道，回文全是對稱的，每個回文串都會有自己的對稱軸，而兩邊都對稱。我們如果從對稱軸開始， 向兩邊闊，如果總相等，就是回文，擴到兩邊不相等的時候，以這個對稱軸向兩邊擴的最長回文串就找到了。
舉例：1 2 1 2 1 2 1 1 1
我們用每一個元素作為對稱軸，向兩邊擴
0位置，左邊沒東西，只有自己；
1位置，判斷左邊右邊是否相等，1=1所以接著擴，然后左邊沒了，所以以1位置為對稱軸的最長回文長度就是3；
2位置，左右都是2，相等，繼續，左右都是1，繼續，左邊沒了，所以最長為5
3位置，左右開始擴，1=1，2=2，1=1，左邊沒了，所以長度是7
如此把每個對稱軸擴一遍，最長的就是答案，對么？
你要是點頭了。。。自己扇自己兩下。
還有偶回文呢，，比如1221，123321.這是什么情況呢？這個對稱軸不是一個具體的數，因為人家是偶回文。
問題三：怎么用對稱軸向兩邊擴的方法找到偶回文？（容易操作的）
我們可以在元素間加上一些符號，比如/1/2/1/2/1/2/1/1/1/，這樣我們再以每個元素為對稱軸擴就沒問題了，每個你加進去的符號都是一個可能的偶數回文對稱軸，此題可解。。。因為我們沒有錯過任何一個可能的對稱軸，不管是奇數回文還是偶數回文。
那么請問，加進去的符號，有什么要求么？是不是必須在原字符中沒出現過？請思考
?
其實不需要的，大家想一下，不管怎么擴，原來的永遠和原來的比較，加進去的永遠和加進去的比較。（不舉例子說明了，自己思考一下）
好，分析一波時間效率吧，對稱軸數量為o(n)級別，每個對稱軸向兩邊能擴多少？最多也就o(n)級別，一共長度才n; 所以n*n是o(n^2) ??(最大能擴的位置其實也是兩個等差數列，這么理解也是o(n^2)，用到剛講的知識)
?
小結：
這種方法把原來的暴力枚舉o(n^3)變成了o(n^2),大家想一想為什么這樣更快呢？
我在kmp一文中就提到過，我們寫出暴力枚舉方法后應想一想自己做出了哪些重復計算，錯過了哪些信息，然后進行優化。
看我們的暴力方法，如果按一般的順序枚舉，012345，012判斷完，接著判斷0123，我是沒想到可以利用前面信息的方法，因為對稱軸不一樣啊，右邊加了一個元素，左邊沒加。所以剛開始，老是想找一種方法，左右都加一個元素，這樣就可以對上一次的信息加以利用了。
暴力為什么效率低？永遠是因為重復計算，舉個例子：12121211，下標從0開始，判斷1212121是否為回文串的時候，其實21212和121等串也就判斷出來了，但是我們并沒有記下結果，當枚舉到21212或者121時，我們依舊是重新嘗試了一遍。(假設主串長度為n，對稱軸越在中間，長度越小的子串，被重復嘗試的越多。中間那些點甚至重復了n次左右，本來一次搞定的事）
還是這個例子，我換一個角度敘述一下，比較直觀，如果從3號開始向兩邊擴，121，21212，最后擴到1212121，時間復雜度o(n),用枚舉的方法要多少時間？如果主串長度為n，枚舉嘗試的子串長度為，3，5，7....n,等差數列，大家讀到這里應該都知道了，等差數列求和，o(n^2)。
三、Manacher原理
首先告訴大家，這個算法時間可以做到o(n),空間o(n).
好的，開始講解這個神奇的算法。
首先明白兩個概念：
最右回文邊界R：挺好理解，就是目前發現的回文串能延伸到的最右端的位置(一個變量解決）
中心c：第一個取得最右回文邊界的那個中心對稱軸；舉個例子:12121，二號元素可以擴到12121，三號元素 可以擴到121，右邊界一樣，我們的中心是二號元素，因為它第一個到達最右邊界
當然，我們還需要一個數組p來記錄每一個可能的對稱軸最后擴到了哪里。
有了這么幾個東西，我們就可以開始這個神奇的算法了。
為了容易理解，我分了四種情況，依次講解：
?
假設遍歷到位置i，如何操作呢
1）i>R:也就是說，i以及i右邊，我們根本不知道是什么，因為從來沒擴到那里。那沒有任何優化，直接往右暴力 擴唄。
（下面我們做i關于c的對稱點，i’）
2）i<R:，
三種情況：
i’的回文左邊界在c回文左邊界的里面
i’回文左邊界在整體回文的外面
i’左邊界和c左邊界是一個元素
(怕你忘了概念，c是對稱中心，c它當初擴到了R，R是目前擴到的最右的地方，現在咱們想以i為中心，看能擴到哪里。)
按原來o(n^2)的方法，直接向兩邊暴力擴。好的，魔性的優化來了。咱們為了好理解，分情況說。首先，大家應該知道的是，i’其實有人家自己的回文長度，我們用數組p記錄了每個位置的情況，所以我們可以知道以i’為中心的回文串有多長。
2-1）i’的回文左邊界在c回文的里面：看圖
我用這兩個括號括起來的就是這兩個點向兩邊擴到的位置，也就是i和i’的回文串，為什么敢確定i回文只有這么長？和i’一樣？我們看c，其實這個圖整體是一個回文串啊。
串內完全對稱(1是括號左邊相鄰的元素，2是右括號右邊相鄰的元素，34同理)，
?由此得出結論1：
由整體回文可知，點2=點3，點1=點4
?
當初i’為什么沒有繼續擴下去？因為點1！=點2。
由此得出結論2：點1！=點2?
?
因為前面兩個結論，所以3！=4，所以i也就到這里就擴不動了。而34中間肯定是回文，因為整體回文，和12中間對稱。
?
2-2）i’回文左邊界在整體回文的外面了：看圖
這時，我們也可以直接確定i能擴到哪里，請聽分析：
當初c的大回文，擴到R為什么就停了？因為點2！=點4----------結論1；
2’為2關于i’的對稱點，當初i’左右為什么能繼續擴呢？說明點2=點2’---------結論2；
由c回文可知2’=3，由結論2可知點2=點2’，所以2=3；
但是由結論一可知，點2！=點4，所以推出3！=4，所以i擴到34為止了，34不等。
而34中間那一部分，因為c回文，和i’在內部的部分一樣，是回文，所以34中間部分是回文。
?
2-3）最后一種當然是i’左邊界和c左邊界是一個元素
點1！=點2，點2=點3，就只能推出這些，只知道34中間肯定是回文，外邊的呢？不知道啊，因為不知道3和4相不相等，所以我們得出結論：點3點4內肯定是，繼續暴力擴。
原理及操作敘述完畢，不知道我講沒講明白。。。
四、代碼及復雜度分析
?看代碼大家是不是覺得不像o(n)？其實確實是的，來分析一波。。
首先，我們的i依次往下遍歷，而R（最右邊界）從來沒有回退過吧？其實當我們的R到了最右邊，就可以結束了。再不濟i自己也能把R一個一個懟到最右
我們看情況一和四，R都是以此判斷就向右一個，移動一次需要o(1)
我們看情況二和三，直接確定了p[i]，根本不用擴，直接遍歷下一個元素去了，每個元素o(1).
綜上，由于i依次向右走，而R也沒有回退過，最差也就是i和R都到了最右邊，而讓它們移動一次的代價都是o(1)的，所以總體o(n)
可能大家看代碼依舊有點懵，其實就是code整合了一下，我們對于情況23，雖然知道了它肯定擴不動，但是我們還是給它一個起碼是回文的范圍，反正它擴一下就沒擴動，不影響時間效率的。而情況四也一樣，給它一個起碼是回文，不用驗證的區域，然后接著擴，四和二三的區別就是。二三我們已經心中有B樹，它肯定擴不動了，而四確實需要接著嘗試。
（要是寫四種情況當然也可以。。但是我懶的寫，太多了。便于理解分了四種情況解釋，code整合后就是這樣子）
?
字數3411
2017/12/22
?
?
前綴樹
是一種哈希樹的變種。典型應用是用于統計，排序和保存大量的字符串（但不僅限于字符串），所以經常被搜索引擎系統用于文本詞頻統計。它的優點是：利用字符串的公共前綴來減少查詢時間，最大限度地減少無謂的字符串比較，查詢效率比哈希樹高。
字典樹又稱為前綴樹或Trie樹，是處理字符串常見的數據結構。假設組成所有單詞的字符僅是“a”~"z"，請實現字典樹結構，并包含以下四個主要功能：
void insert(String word)：添加word，可重復添加。
void delete(String word)：刪除word，如果word添加過多次，僅刪除一次。
boolean search(String word)：查詢word是否在字典樹中。
int prefixNumber(String pre)：返回以字符串pre為前綴的單詞數量。
思考：
字典樹的介紹。字典樹是一種樹形結構，優點是利用字符串的公共前綴來節約存儲空間。
?
基本性質：
字典樹的基本性質如下：
- 根節點沒有字符路徑。除根節點外，每一個節點都被一個字符路徑找到。
- 從根節點到某一節點，將路徑上經過的字符連接起來，為掃過的對應字符串。
- 每個節點向下所有的字符路徑上的字符都不同。
也不需要記，看了實現，很自然的性質就理解了。
每個結點內有一個指針數組，里面有二十六個指針，分別指向二十六個字母。
如果指向某個字母的指針為空，那就是以前沒有遇到過這個前綴。
?
搜索的方法為：
(1) 從根結點開始一次搜索；
(2) 取得要查找關鍵詞的第一個字母，并根據該字母選擇對應的子樹并轉到該子樹繼續進行檢索；
(3) 在相應的子樹上，取得要查找關鍵詞的第二個字母,并進一步選擇對應的子樹進行檢索。
(4) 迭代過程……
(5) 在某個結點處，關鍵詞的所有字母已被取出，則讀取附在該結點上的信息，即完成查找。
其他操作類似處理
插入也一樣，只是轉到某個子樹時，沒有子樹，那就創建一個新節點，然后對應指針指向新節點即可。
我們給出定義就更清楚了：
public static class TrieNode {public int path; //表示由多少個字符串共用這個節點public int end;//表示有多少個字符串是以這個節點結尾的public TrieNode[] map;//哈希表結構，key代表該節點的一條字符路徑，value表示字符路徑指向的節點public TrieNode() {path = 0;end = 0;map = new TrieNode[26];}
}path和end都是有用的，接下來會說明
insert：
public static class Trie {private TrieNode root;//頭public Trie() {root = new TrieNode();}public void insert(String word) {if (word == null) {return;}//空串char[] chs = word.toCharArray();TrieNode node = root;int index = 0; //哪條路for (int i = 0; i < chs.length; i++) {index = chs[i] - 'a'; //0~25if (node.map[index] == null) {node.map[index] = new TrieNode();}//創建，繼續node = node.map[index];//指向子樹node.path++;//經過加1}node.end++;//本單詞個數加1} public boolean search(String word) {if (word == null) {return false;}char[] chs = word.toCharArray();TrieNode node = root;int index = 0;for (int i = 0; i < chs.length; i++) {index = chs[i] - 'a';if (node.map[index] == null) {return false;//找不到}node = node.map[index];}return node.end != 0;//end標記有沒有以這個字符為結尾的字符串}delete：?
public void delete(String word) {//如果有if (search(word)) {char[] chs = word.toCharArray();TrieNode node = root;int index = 0;for (int i = 0; i < chs.length; i++) {index = chs[i] - 'a';if (node.map[index].path-- == 1) {//path減完之后為0node.map[index] = null;return;}node = node.map[index];//去子樹}node.end--;//次數減1}}prefixNumber：
public int prefixNumber(String pre) {if (pre == null) {return 0;}char[] chs = pre.toCharArray();TrieNode node = root;int index = 0;for (int i = 0; i < chs.length; i++) {index = chs[i] - 'a';if (node.map[index] == null) {return 0;//找不到}node = node.map[index];}return node.path;//返回經過的次數即可}好處：
1.利用字符串的公共前綴來節約存儲空間。
2.最大限度地減少無謂的字符串比較，查詢效率比較高。例如：若要查找的字符長度是5，而總共有單詞的數目是26^5＝11881376，利用trie樹，利用5次比較可以從11881376個可能的關鍵字中檢索出指定的關鍵字，而利用二叉查找樹時間復雜度是O( log2n?)，所以至少要進行log211881376=23.5次比較。可以看出來利用字典樹進行查找速度是比較快的。
?
應用：
<1.字符串的快速檢索
<2.字符串排序
<3.最長公共前綴：abdh和abdi的最長公共前綴是abd，遍歷字典樹到字母d時，此時這些單詞的公共前綴是abd。
<4.自動匹配前綴顯示后綴
我們使用辭典或者是搜索引擎的時候，輸入appl，后面會自動顯示一堆前綴是appl的東東吧。
那么有可能是通過字典樹實現的，前面也說了字典樹可以找到公共前綴，我們只需要把剩余的后綴遍歷顯示出來即可。
?
相關題目：
一個字符串類型的數組arr1，另一個字符串類型的數組arr2。
arr2中有哪些字符，是arr1中出現的？請打印。
arr2中有哪些字符，是作為arr1中某個字符串前綴出現的？請打印。
arr2中有哪些字符，是作為arr1中某個字符串前綴出現的？請打印arr2中出現次數最大的前綴。
?
后綴樹/后綴數組
字典樹：https://blog.csdn.net/hebtu666/article/details/83141560
后綴樹：后綴樹，就是把一串字符的所有后綴保存并且壓縮的字典樹。
?
相對于字典樹來說，后綴樹并不是針對大量字符串的，而是針對一個或幾個字符串來解決問題。比如字符串的回文子串，兩個字符串的最長公共子串等等。
比如單詞banana，它的所有后綴顯示到下面的。0代表從第一個字符為起點，終點不用說都是字符串的末尾。
以上面的后綴，我們建立一顆后綴樹。如下圖，為了方便看到后綴，我沒有合并相同的前綴。
把非公共部分壓縮：
后綴樹的應用：
（1）查找某個字符串s1是否在另外一個字符串s2中：如果s1在字符串s2中，那么s1必定是s2中某個后綴串的前綴。
（2）指定字符串s1在字符串s2中重復的次數：比如說banana是s1，an是s2，那么計算an出現的次數實際上就是看an是幾個后綴串的前綴。
（3）兩個字符串S1，S2的最長公共部分（廣義后綴樹）
（4）最長回文串（廣義后綴樹）
?
關于后綴樹的實現和應用以后再寫，這次主要寫后綴數組。
在字符串處理當中，后綴樹和后綴數組都是非常有力的工具。其實后綴數組是后綴樹的一個非常精巧的替代品，它比后綴樹容易編程實現，能夠實現后綴樹的很多功能而時間復雜度也不太遜色，并且，它比后綴樹所占用的空間小很多。可以說，在信息學競賽中后綴數組比后綴樹要更為實用。
?
后綴數組：就是把某個字符串的所有后綴按照字典序排序后的數組。（數組中保存起始位置就好了，結束位置一定是最后）
先說如何計算后綴數組：
倍增的思想，我們先把每個長度為2的子串排序，再利用結果把每個長度為4的字串排序，再利用結果排序長度為8的子串。。。直到長度大于等于串長。
設置sa[]數組來記錄排名：sa[i]代表排第i名的是第幾個串。
結果用rank[]數組返回，rank[i]記錄的是起始位置為第i個字符的后綴排名第幾小。
我們開始執行過程：
比如字符串abracadabra
長度為2的排名：a ab ab ac ad br br ca da ra ra,他們分別排第0，1，2，2，3，4，5，5，6，7，8，8名
sa數組就是11(空串),10(a),0(ab),7,3,5,1,8,4,6,2,9(ra排名最后)
這樣，所有長度為2的子串的排名就出來了，我們如何利用排名把長度為4的排名搞出來呢？
abracadabra中，ab,br,ra這些串排名知道了。我們把他們兩兩合并為長度為4的串，進行排名。
比如abra和brac怎么比較呢？
用原來排名的數對來表示
abra=ab+ra=1+8
brac=br+ac=4+2
對于字符串的字典序，這個例子比1和4就比出來了。
如果第一個數一樣，也就是前兩個字符一樣，那再比后面就可以了。
簡單說就是先比前一半字符的排名，再比后一半的排名。
具體實現，我們可以用系統sort，傳一個比較器就好了。
?
還有需要注意，長度不可能那么湊巧是2^n，所以 一般的，k=n時，rank[i]表示從位置i開始向后n個字符的排名第幾小，而剩下不足看個字符，rank[i]代表從第i個字符到最后的串的排名第幾小，也就是后綴。
保證了每一個后綴都能正確表示并排序。比如k=4時，就表示出了長度為1，2，3的后綴：a,ra,bra.這就保證了k=8時，長度為5，6，7的后綴也能被表示出來：4+1，4+2，4+3
還有，sa[0]永遠是空串，空串的排名rank[sa[0]]永遠是最大。
int n;
int k;
int rank[MAX_N+1];//結果（排名）數組
int tmp[MAX_N+1];//臨時數組
//定義比較器
bool compare(int i,int j)
{if(rank[i]!=rank[j])return rank[i]<rank[j];//長度為k的子串的比較int ri=i+k<=n ? rank[i+k] : -1;int rj=j+k<=n ? rank[j+k] : -1;return ri<rj;
}void solve(string s,int *sa)
{n=s.length;//長度為1時，按字符碼即可，長度為2時就可以直接用for(int i=0;i<=n;i++){sa[i]=i;rank[i]=i<n ? s[i] : -1;//注意空串為最大}//由k對2k排序，直到超范圍for(k=1;k<=n;k*=2){sort(sa,sa+n+1,compare);tmp[sa[0]=0;//空串for(int i=1;i<=n;i++){tmp[sa[i]]=tmp[sa[i-1]]+(compare(sa[i-1],sa[i]) ? 1 : 0);//注意有相同的}for(int i=0;i<=n;i++){rank[i]=tmp[i];}}
}具體應用以后再寫。。。。。
?
AC自動機
今天寫一下基本的AC自動機的思想原理和實現。
Aho-Corasick automation，該算法在1975年產生于貝爾實驗室，是著名的多模匹配算法之一。一個常見的例子就是給出n個單詞，再給出一段包含m個字符的文章，讓你找出有多少個單詞在文章里出現過。要搞懂AC自動機，先得有模式樹（字典樹）Trie和KMP模式匹配算法的基礎知識。
KMP算法是單模式串的字符匹配算法，AC自動機是多模式串的字符匹配算法。
首先我們回憶一下KMP算法：失配之后，子串通過next數組找到應該匹配的位置，也就是最長相等前后綴。
AC自動機也是一樣，只不過是匹配到當前失配之后，找到當前字符串的后綴，和所有字符串的前綴，找出最長相等前后綴。
就這么簡單。
當然，字典樹的知識是需要了解的。
我就默認讀者都會字典樹了。
我們操作的第一步就是把那些單詞做一個字典樹出來，這個好理解。
?
在AC自動機中，我們也有類似next數組的東西就是fail指針，當發現失配的字符失配的時候，跳轉到fail指針指向的位置，然后再次進行匹配操作。
當前節點t有fail指針，其fail指針所指向的節點和t所代表的字符是相同的。因為t匹配成功后，我們需要去匹配t->child，發現失配，那么就從t->fail這個節點開始再次去進行匹配。
KMP里有詳細講解過程，我就不占篇幅敘述了。
然后說一下fail指針如何建立：
和next數組大同小異。如果你很熟悉next數組的建立，fail指針也是一樣的。
假設當前節點為father，其孩子節點記為child。求child的Fail指針時，首先我們要找到其father的Fail指針所指向的節點,假如是t的話，我們就要看t的孩子中有沒有和child節點所表示的字母相同的節點，如果有的話，這個節點就是child的fail指針，如果發現沒有，則需要找father->fail->fail這個節點，然后重復上面過程，如果一直找都找不到，則child的Fail指針就要指向root。
KMP也是一樣的的操作：p[next[i-1]]，p[next[next[i-1]]]這樣依次往前跳啊。
?
如果跳轉，跳轉后的串的前綴，必為跳轉前的模式串的后綴，并且跳轉的新位置的深度（匹配字符個數）一定小于跳之前的節點。所以我們可以利用 bfs在 Trie上面進行 fail指針的求解。流程和NEXT數組類似。
?
匹配的時候流程也是基本一樣的，請參考KMP或者直接看代碼：
HDU 2222?Keywords Search? ? 最基本的入門題了
就是求目標串中出現了幾個模式串。
很基礎了。使用一個int型的end數組記錄，查詢一次。
#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <queue>
using namespace std;struct Trie
{int next[500010][26],fail[500010],end[500010];int root,L;int newnode(){for(int i = 0;i < 26;i++)next[L][i] = -1;end[L++] = 0;return L-1;}void init(){L = 0;root = newnode();}void insert(char buf[]){int len = strlen(buf);int now = root;for(int i = 0;i < len;i++){if(next[now][buf[i]-'a'] == -1)next[now][buf[i]-'a'] = newnode();now = next[now][buf[i]-'a'];}end[now]++;}void build()//建樹{queue<int>Q;fail[root] = root;for(int i = 0;i < 26;i++)if(next[root][i] == -1)next[root][i] = root;else{fail[next[root][i]] = root;Q.push(next[root][i]);}while( !Q.empty() )//建fail{int now = Q.front();Q.pop();for(int i = 0;i < 26;i++)if(next[now][i] == -1)next[now][i] = next[fail[now]][i];else{fail[next[now][i]]=next[fail[now]][i];Q.push(next[now][i]);}}}int query(char buf[])//匹配{int len = strlen(buf);int now = root;int res = 0;for(int i = 0;i < len;i++){now = next[now][buf[i]-'a'];int temp = now;while( temp != root ){res += end[temp];end[temp] = 0;temp = fail[temp];}}return res;}void debug(){for(int i = 0;i < L;i++){printf("id = %3d,fail = %3d,end = %3d,chi = [",i,fail[i],end[i]);for(int j = 0;j < 26;j++)printf("%2d",next[i][j]);printf("]\n");}}
};
char buf[1000010];
Trie ac;
int main()
{int T;int n;scanf("%d",&T);while( T-- ){scanf("%d",&n);ac.init();for(int i = 0;i < n;i++){scanf("%s",buf);ac.insert(buf);}ac.build();scanf("%s",buf);printf("%d\n",ac.query(buf));}return 0;
}?
數組缺失
?
二叉樹遍歷
二叉樹：二叉樹是每個節點最多有兩個子樹的樹結構。
?
本文介紹二叉樹的遍歷相關知識。
我們學過的基本遍歷方法，無非那么幾個：前序，中序，后序，還有按層遍歷等等。
設L、D、R分別表示遍歷左子樹、訪問根結點和遍歷右子樹， 則對一棵二叉樹的遍歷有三種情況：DLR（稱為先根次序遍歷），LDR（稱為中根次序遍歷），LRD （稱為后根次序遍歷）。
首先我們定義一顆二叉樹
typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{ElementType Data;BinTree Left;BinTree Right;
};
前序
首先訪問根，再先序遍歷左（右）子樹，最后先序遍歷右（左）子樹
思路：
就是利用函數，先打印本個節點，然后對左右子樹重復此過程即可。
void PreorderTraversal( BinTree BT )
{if(BT==NULL)return ;printf(" %c", BT->Data);PreorderTraversal(BT->Left);PreorderTraversal(BT->Right);
}?
中序
首先中序遍歷左（右）子樹，再訪問根，最后中序遍歷右（左）子樹
思路：
還是利用函數，先對左邊重復此過程，然后打印根，然后對右子樹重復。
void InorderTraversal( BinTree BT )
{if(BT==NULL)return ;InorderTraversal(BT->Left);printf(" %c", BT->Data);InorderTraversal(BT->Right);
}后序
首先后序遍歷左（右）子樹，再后序遍歷右（左）子樹，最后訪問根
思路：
先分別對左右子樹重復此過程，然后打印根
void PostorderTraversal(BinTree BT)
{if(BT==NULL)return ;PostorderTraversal(BT->Left);PostorderTraversal(BT->Right);printf(" %c", BT->Data);
}進一步思考
看似好像很容易地寫出了三種遍歷。。。。。
?
但是你真的理解為什么這么寫嗎？
比如前序遍歷，我們真的是按照定義里所講的，首先訪問根，再先序遍歷左（右）子樹，最后先序遍歷右（左）子樹。這種過程來遍歷了一遍二叉樹嗎？
仔細想想，其實有一絲不對勁的。。。
再看代碼：
void Traversal(BinTree BT)//遍歷
{
//1111111111111Traversal(BT->Left);
//22222222222222Traversal(BT->Right);
//33333333333333
}為了敘述清楚，我給三個位置編了號?1，2，3
我們憑什么能前序遍歷，或者中序遍歷，后序遍歷？
我們看，前序中序后序遍歷，實現的代碼其實是類似的，都是上面這種格式，只是我們分別在位置1，2，3打印出了當前節點而已啊。我們憑什么認為，在1打印，就是前序，在2打印，就是中序，在3打印，就是后序呢？不管在位置1，2，3哪里操作，做什么操作，我們利用函數遍歷樹的順序變過嗎？當然沒有啊。。。
都是三次返回到當前節點的過程：先到本個節點，也就是位置1，然后調用了其他函數，最后調用完了，我們開到了位置2。然后又調用別的函數，調用完了，我們來到了位置3.。然后，最后操作完了，這個函數才結束。代碼里的三個位置，每個節點都被訪問了三次。
而且不管位置1，2，3打印了沒有，操作了沒有，這個順序是永遠存在的，不會因為你在位置1打印了，順序就改為前序，你在位置2打印了，順序就成了中序。
?
為了有更直觀的印象，我們做個試驗：在位置1，2，3全都放入打印操作；
我們會發現，每個節點都被打印了三次。而把每個數第一次出現拿出來，就組成了前序遍歷的序列；所有數字第二次出現拿出來，就組成了中序遍歷的序列。。。。
?
其實，遍歷是利用了一種數據結構：棧
而我們這種寫法，只是通過函數，來讓系統幫我們壓了棧而已。為什么能實現遍歷？為什么我們訪問完了左子樹，能返回到當前節點？這都是棧的功勞啊。我們把當前節點（對于函數就是當時的現場信息）存到了棧里，記錄下來，后來才能把它拿了出來，能回到以前的節點。
?
想到這里，可能就有更深刻的理解了。
我們能否不用函數，不用系統幫我們壓棧，而是自己做一個棧，來實現遍歷呢？
先序實現思路：拿到一個節點的指針，先判斷是否為空，不為空就先訪問（打印）該結點，然后直接進棧，接著遍歷左子樹；為空則要從棧中彈出一個節點來，這個時候彈出的結點就是其父親，然后訪問其父親的右子樹，直到當前節點為空且棧為空時，結束。
核心思路代碼實現：
*p=root;
while(p || !st.empty())
{if(p)//非空{//visit(p);進行操作st.push(p);//入棧p = p->lchild;左} else//空{p = st.top();//取出st.pop();p = p->rchild;//右}
}中序實現思路：和前序遍歷一樣，只不過在訪問節點的時候順序不一樣，訪問節點的時機是從棧中彈出元素時訪問，如果從棧中彈出元素，就意味著當前節點父親的左子樹已經遍歷完成，這時候訪問父親，就是中序遍歷.
（對應遞歸是第二次遇到）
核心代碼實現：
*p=root;
while(p || !st.empty())
{if(p)//非空{st.push(p);//壓入p = p->lchild;}else//空{p = st.top();//取出//visit(p);操作st.pop();p = p->rchild;}
}后序遍歷是最難的。因為要保證左孩子和右孩子都已被訪問并且左孩子在右孩子前訪問才能訪問根結點，這就為流程的控制帶來了難點。
因為我們原來說了，后序是第三次遇到才進行操作的，所以我們很容易有這種和遞歸函數類似的思路：對于任一結點，將其入棧，然后沿其左子樹一直往下走，一直走到沒有左孩子的結點，此時該結點在棧頂，但是不能出棧訪問， 因此右孩子還沒訪問。所以接下來按照相同的規則對其右子樹進行相同的處理。訪問完右孩子，該結點又出現在棧頂，此時可以將其出棧并訪問。這樣就保證了正確的訪問順序。可以看出，在這個過程中，每個結點都兩次出現在棧頂，只有在第二次出現在棧頂時，才能訪問它。因此需要多設置一個變量標識該結點是否是第一次出現在棧頂。
第二種思路：對于任一結點P，先將其入棧。如果P不存在左孩子和右孩子，或者左孩子和右孩子都已被訪問過了，就可以直接訪問該結點。如果有孩子未訪問，將P的右孩子和左孩子依次入棧。
網上的思路大多是第一種，所以我在這里給出第二種的大概實現吧
首先初始化cur，pre兩個指針，代表訪問的當前節點和之前訪問的節點。把根放入，開始執行。
s.push(root);
while(!s.empty())
{cur=s.top();if((cur->lchild==NULL && cur->rchild==NULL)||(pre!=NULL && (pre==cur->lchild||pre==cur->rchild))){//visit(cur); 如果當前結點沒有孩子結點或者孩子節點都已被訪問過 s.pop();//彈出pre=cur; //記錄}else//分別放入右左孩子{if(cur->rchild!=NULL)s.push(cur->rchild);if(cur->lchild!=NULL) s.push(cur->lchild);}
}這兩種方法，都是利用棧結構來實現的遍歷，需要一定的棧空間，而其實存在一種時間O(N),空間O(1)的遍歷方式，下次寫了我再放鏈接。
?
斗個小機靈：后序是LRD，我們其實已經知道先序是DLR，那其實我們可以用先序來實現后序啊，我們只要先序的時候把左右子樹換一下：DRL（這一步很好做到），然后倒過來不就是DRL了嘛。。。。。就把先序代碼改的左右反過來，然后放棧里倒過來就好了，不需要上面介紹的那些復雜的方法。。。。
?
二叉樹序列化/反序列化
二叉樹被記錄成文件的過程，為二叉樹的序列化
通過文件重新建立原來的二叉樹的過程，為二叉樹的反序列化
設計方案并實現。
（已知結點類型為32位整型）
?
思路：先序遍歷實現。
因為要寫入文件，我們要把二叉樹序列化為一個字符串。
首先，我們要規定，一個結點結束后的標志：“！”
然后就可以通過先序遍歷生成先序序列了。
?
但是，眾所周知，只靠先序序列是無法確定一個唯一的二叉樹的，原因分析如下：
比如序列1！2！3！
我們知道1是根，但是對于2，可以作為左孩子，也可以作為右孩子：
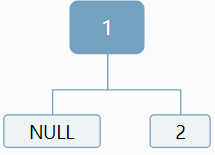
對于3，我們仍然無法確定，應該作為左孩子還是右孩子，情況顯得更加復雜：
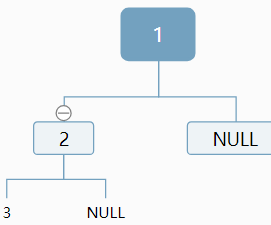
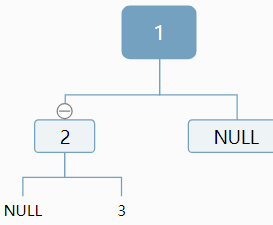
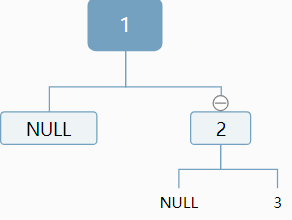
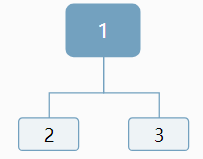
原因：我們對于當前結點，插入新結點是無法判斷插入位置，是應該作為左孩子，還是作為右孩子。
因為我們的NULL并未表示出來。
如果我們把NULL也用一個符號表示出來：
比如
1！2！#！#！3！#！#！
我們再按照先序遍歷的順序重建：
對于1，插入2時，就確定要作為左孩子，因為左孩子不為空。
然后接下來兩個#，我們就知道了2的左右孩子為空，然后重建1的右子樹即可。
?
我們定義結點：
public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}序列化：
public static String serialByPre(Node head) {if (head == null) {return "#!";}String res = head.value + "!";res += serialByPre(head.left);res += serialByPre(head.right);return res;}?
public static Node reconByPreString(String preStr) {//先把字符串轉化為結點序列String[] values = preStr.split("!");Queue<String> queue = new LinkedList<String>();for (int i = 0; i != values.length; i++) {queue.offer(values[i]);}return reconPreOrder(queue);}public static Node reconPreOrder(Queue<String> queue) {String value = queue.poll();if (value.equals("#")) {return null;//遇空}Node head = new Node(Integer.valueOf(value));head.left = reconPreOrder(queue);head.right = reconPreOrder(queue);return head;}這樣并未改變先序遍歷的時空復雜度，解決了先序序列確定唯一一顆樹的問題，實現了二叉樹序列化和反序列化。
?
先序中序后序兩兩結合重建二叉樹
遍歷是對樹的一種最基本的運算，所謂遍歷二叉樹，就是按一定的規則和順序走遍二叉樹的所有結點，使每一個結點都被訪問一次，而且只被訪問一次。由于二叉樹是非線性結構，因此，樹的遍歷實質上是將二叉樹的各個結點轉換成為一個線性序列來表示。
設L、D、R分別表示遍歷左子樹、訪問根結點和遍歷右子樹， 則對一棵二叉樹的遍歷有三種情況：DLR（稱為先根次序遍歷），LDR（稱為中根次序遍歷），LRD （稱為后根次序遍歷）。
先序遍歷
首先訪問根，再先序遍歷左（右）子樹，最后先序遍歷右（左）子樹，C語言代碼如下：
| 1 2 3 4 5 6 7 |
|
中序遍歷
首先中序遍歷左（右）子樹，再訪問根，最后中序遍歷右（左）子樹，C語言代碼如下
| 1 2 3 4 5 6 7 8 |
|
后序遍歷
首先后序遍歷左（右）子樹，再后序遍歷右（左）子樹，最后訪問根，C語言代碼如下
| 1 2 3 4 5 6 7 |
|
層次遍歷
即按照層次訪問，通常用隊列來做。訪問根，訪問子女，再訪問子女的子女（越往后的層次越低）（兩個子女的級別相同）
?
輸入某二叉樹的前序遍歷和中序遍歷的結果，請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重復的數字。例如輸入前序遍歷序列{1,2,4,7,3,5,6,8}和中序遍歷序列{4,7,2,1,5,3,8,6}，則重建二叉樹并返回。
?
我們首先找到根結點：一定是先序遍歷序列的第一個元素：1
然后，在中序序列尋找根，把中序序列分為兩個序列左子樹4，7，2和右子樹5，3，8，6
把先序序列也分為兩個：? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?左子樹2，4，7和右子樹3，5，6，8
對左右重復同樣的過程：
先看左子樹：先序序列4，7，2，說明4一定是左子樹的根
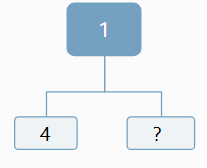
把2，4，7分為2和7兩個序列，再重復過程，左邊確定完畢。
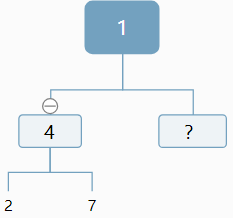
右子樹同樣：中序序列為5，3，8，6，先序序列為：3，5，6，8
取先序頭，3.一定是根
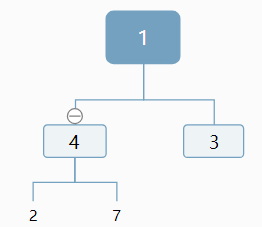
把中序序列分為? ? ?5和8，6兩個序列
對應的先序序列為 5和6，8兩個序列
?
然后確定了5是3的左孩子
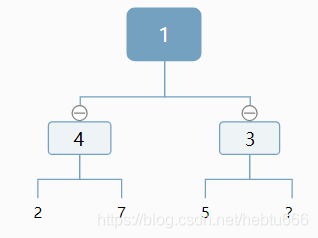
對于先序序列6，8和中序序列8，6
還是先取先序的頭，6
?
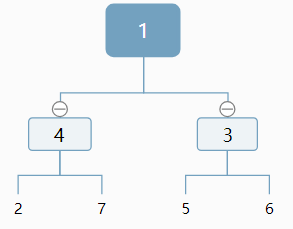
現在只有8，中序序列8在左邊，是左孩子。
結束。
我們總結一下這種方法的過程：
1、根據先序序列確定當前樹的根（第一個元素）。
2、在中序序列中找到根，并以根為分界分為兩個序列。
3、這樣，確定了左子樹元素個數，把先序序列也分為兩個。
對左右子樹（對應的序列）重復相同的過程。
?
我們把思路用代碼實現：
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:# 返回構造的TreeNode根節點def reConstructBinaryTree(self, pre, tin):# write code here/#pre-先序數組 tin->中序數組if len(pre) == 0:return Noneroot = TreeNode(pre[0])//第一個元素為根pos = tin.index(pre[0])//劃分左右子樹root.left = self.reConstructBinaryTree( pre[1:1+pos], tin[:pos])root.right = self.reConstructBinaryTree( pre[pos+1:], tin[pos+1:])return root
輸入某二叉樹的后序遍歷和中序遍歷的結果，請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重復的數字
?
思路是類似的，只是我們確定根的時候，取后序序列的最后一個元素即可。
?
輸入某二叉樹的后序遍歷和先序遍歷的結果，請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重復的數字
?
我們直白的表述一下，前序是中左右，后序是左右中。
所以，我們憑先序和后序序列其實是無法判斷根的孩子到底是左孩子還是右孩子。
比如先序序列1，5，后序序列是5，1
我們只知道1是這棵樹的根，但是我們不知道5是1的左孩子還是右孩子。
我們的中序序列是左中右，才可以明確的劃分出左右子樹，而先序后序不可以。
?
綜上，只有，只含葉子結點或者同時有左右孩子的結點的樹，才可以被先序序列后序序列確定唯一一棵樹。
最后不斷劃分先序和后序序列完成重建。
?
先序中序數組推后序數組
二叉樹遍歷
所謂遍歷(Traversal)是指沿著某條搜索路線，依次對樹中每個結點均做一次且僅做一次訪問。訪問結點所做的操作依賴于具體的應用問 題。 遍歷是二叉樹上最重要的運算之一，是二叉樹上進行其它運算之基礎。
?
從二叉樹的遞歸定義可知，一棵非空的二叉樹由根結點及左、右子樹這三個基本部分組成。因此，在任一給定結點上，可以按某種次序執行三個操作：
⑴訪問結點本身（N），
⑵遍歷該結點的左子樹（L），
⑶遍歷該結點的右子樹（R）。
以上三種操作有六種執行次序：
NLR、LNR、LRN、NRL、RNL、RLN。
注意：
前三種次序與后三種次序對稱，故只討論先左后右的前三種次序。
遍歷命名
根據訪問結點操作發生位置命名：
① NLR：前序遍歷(Preorder Traversal 亦稱（先序遍歷））
——訪問根結點的操作發生在遍歷其左右子樹之前。
② LNR：中序遍歷(Inorder Traversal)
——訪問根結點的操作發生在遍歷其左右子樹之中（間）。
③ LRN：后序遍歷(Postorder Traversal)
——訪問根結點的操作發生在遍歷其左右子樹之后。
注意：
由于被訪問的結點必是某子樹的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解釋為根、根的左子樹和根的右子樹。NLR、LNR和LRN分別又稱為先根遍歷、中根遍歷和后根遍歷。
?
給出某棵樹的先序遍歷結果和中序遍歷結果（無重復值），求后序遍歷結果。
比如
先序序列為：1，2，4，5，3，6，7，8，9
中序序列為：4，2，5，1，6，3，7，9，8
方法1：我們可以重建整棵樹：
https://blog.csdn.net/hebtu666/article/details/84322113
建議好好看這個網址，對理解這個方法有幫助。
?
如圖
然后后序遍歷得出后序序列。
?
方法2：我們可以不用重建，直接得出：
過程：
1）根據當前先序數組，設置后序數組最右邊的值
2）劃分出左子樹的先序、中序數組和右子樹的先序、中序數組
3）對右子樹重復同樣的過程
4）對左子樹重復同樣的過程
?
原因：我們的后序遍歷是左右中的，也就是先左子樹，再右子樹，再根
舉個例子：
比如這是待填充序列：
我們確定了根，并且根據根和中序序列劃分出了左右子樹，黃色部分為左子樹：
：
先處理右子樹（其實左右中反過來就是中右左，順著填就好了）：
我們又確定了右子樹的右子樹為黑色區域，然后接著填右子樹的右子樹的根（N)即可。
?
?
舉例說明：
a[]先序序列為：1，2，4，5，3，6，7，8，9
b[]中序序列為：4，2，5，1，6，3，7，9，8
c[]后序序列為：0，0，0，0，0，0，0，0，0（0代表未確定）
我們根據先序序列，知道根一定是1，所以后序序列：0，0，0，0，0，0，0，0，1
從b[]中找到1，并劃分數組：
? ? ? ? ? 左子樹的先序：2，4，5，
? ? ? ? ? 中序：4，2，5
? ? ? ? ? 右子樹的先序：3，6，7，8，9，
? ? ? ? ? 中序：6，3，7，9，8
?
我們繼續對右子樹重復相同的過程：
（圖示為當前操作的樹，我們是不知道這棵樹的樣子的，我是為了方便敘述，圖片表達一下當前處理的位置）
當前樹的根一定為先序序列的第一個元素，3，所以我們知道后序序列：0，0，0，0，0，0，0，3，1
我們繼續對左右子樹進行劃分，中序序列為6，3，7，9，8，我們在序列中找到2，并劃分為左右子樹：
左子樹：
先序序列：6
中序序列：6
右子樹：
先序序列：7，8，9
中序序列：7，9，8
我們繼續對右子樹重復相同的過程，也就是如圖所示的這棵樹：
現在我們的后序序列為0，0，0，0，0，0，0，3，1
這時我們繼續取當前的根（先序第一個元素）放在下一個后序位置：0，0，0，0，0，0，7，3，1
劃分左右子樹：
左子樹：空，也就是它
右子樹：先序8，9，中序9，8，也就是這個樹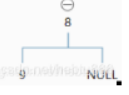
我們繼續處理右子樹：先序序列為8，9，所以根為8，我們繼續填后序數組0，0，0，0，0，8，7，3，1
然后劃分左右子樹：
左子樹：先序：9，中序：9
右子樹：空
對于左子樹，一樣，我們取頭填后序數組0，0，0，0，9，8，7，3，1，然后發現左右子樹都為空.
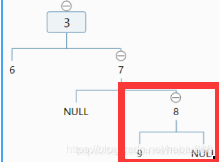我們就把這個小框框處理完了
然后這棵樹的右子樹就處理完了，處理左子樹，發現為空。這棵樹也處理完了。
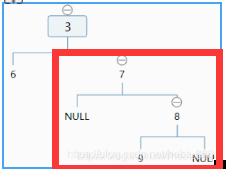這一堆就完了。我們處理以3為根的二叉樹的左子樹。繼續填后序數組：
0，0，0，6，9，8，7，3，1
整棵樹的右子樹處理完了，左子樹同樣重復這個過程。
最后4，5，2，6，9，8，7，3，1
?
好累啊。。。。。。挺簡單個事寫了這么多。
回憶一下過程：
1）根據當前先序數組，設置后序數組最右邊的值
2）劃分出左子樹的先序、中序數組和右子樹的先序、中序數組
3）對右子樹重復同樣的過程
4）對左子樹重復同樣的過程
就這么簡單
?
先填右子樹是為了數組連續填充，容易理解，先處理左子樹也可以。
最后放上代碼吧
a=[1,2,4,5,3,6,7,8,9]
b=[4,2,5,1,6,3,7,9,8]
l=[0,0,0,0,0,0,0,0,0]def f(pre,tin,x,y):#x,y為樹在后序數組中對應的范圍if pre==[]:returnl[y]=pre[0]#根pos=tin.index(pre[0])#左子樹元素個數f(pre[pos+1:],tin[pos+1:],x+pos,y-1)#處理右子樹f(pre[1:pos+1],tin[:pos],x,x+pos-1)#處理左子樹f(a,b,0,len(l)-1)
print(l)
根據數組建立平衡二叉搜索樹
它是一 棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，并且左右兩個子樹都是一棵平衡二叉（搜索）樹。
?
二分：用有序數組中中間的數生成搜索二叉樹的頭節點，然后對數組的左右部分分別生成左右子樹即可（重復過程）。
生成的二叉樹中序遍歷一定還是這個序列。
?
非常簡單，不過多敘述：
public class SortedArrayToBalancedBST {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static Node generateTree(int[] sortArr) {if (sortArr == null) {return null;}return generate(sortArr, 0, sortArr.length - 1);}public static Node generate(int[] sortArr, int start, int end) {if (start > end) {return null;}int mid = (start + end) / 2;Node head = new Node(sortArr[mid]);head.left = generate(sortArr, start, mid - 1);head.right = generate(sortArr, mid + 1, end);return head;}// for test -- print treepublic static void printTree(Node head) {System.out.println("Binary Tree:");printInOrder(head, 0, "H", 17);System.out.println();}public static void printInOrder(Node head, int height, String to, int len) {if (head == null) {return;}printInOrder(head.right, height + 1, "v", len);String val = to + head.value + to;int lenM = val.length();int lenL = (len - lenM) / 2;int lenR = len - lenM - lenL;val = getSpace(lenL) + val + getSpace(lenR);System.out.println(getSpace(height * len) + val);printInOrder(head.left, height + 1, "^", len);}public static String getSpace(int num) {String space = " ";StringBuffer buf = new StringBuffer("");for (int i = 0; i < num; i++) {buf.append(space);}return buf.toString();}public static void main(String[] args) {int[] arr = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };printTree(generateTree(arr));}}
java整體打印二叉樹
一個調的很好的打印二叉樹的代碼。
用空格和^v來表示節點之間的關系。
效果是這樣：
Binary Tree:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?v7v ? ? ??
? ? ? ? ? ? ? ? ? ? ? ? v6v ? ? ??
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?^5^ ? ? ??
? ? ? ?H4H ? ? ??
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?v3v ? ? ??
? ? ? ? ? ? ? ? ? ? ? ? ^2^ ? ? ??
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?^1^ ?
?
對于每個節點，先打印右子樹，然后打印本身，然后打印左子樹。
?
public class fan {public static class Node {public int value;Node left;Node right;public Node(int data) {this.value = data;}}public static void printTree(Node head) {System.out.println("Binary Tree:");printInOrder(head, 0, "H", 17);System.out.println();}public static void printInOrder(Node head, int height, String to, int len) {if (head == null) {return;}printInOrder(head.right, height + 1, "v", len);String val = to + head.value + to;int lenM = val.length();int lenL = (len - lenM) / 2;int lenR = len - lenM - lenL;val = getSpace(lenL) + val + getSpace(lenR);System.out.println(getSpace(height * len) + val);printInOrder(head.left, height + 1, "^", len);}public static String getSpace(int num) {String space = " ";StringBuffer buf = new StringBuffer("");for (int i = 0; i < num; i++) {buf.append(space);}return buf.toString();}public static void main(String[] args) {Node head = new Node(4);head.left = new Node(2);head.right = new Node(6);head.left.left = new Node(1);head.left.right = new Node(3);head.right.left = new Node(5);head.right.right = new Node(7);printTree(head);}}
判斷平衡二叉樹
平衡二叉樹（Balanced Binary Tree）具有以下性質：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1。并且左右兩個子樹都是一棵平衡二叉樹
（不是我們平時意義上的必須為搜索樹）
判斷一棵樹是否為平衡二叉樹：
?
可以暴力判斷：每一顆樹是否為平衡二叉樹。
?
分析：
如果左右子樹都已知是平衡二叉樹，而左子樹和右子樹高度差絕對值不超過1，本樹就是平衡的。
?
為此我們需要的信息：左右子樹是否為平衡二叉樹。左右子樹的高度。
?
我們需要給父返回的信息就是：本棵樹是否是平衡的、本棵樹的高度。
?
定義結點和返回值：
public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}} public static class ReturnType {public int level; //深度public boolean isB;//本樹是否平衡public ReturnType(int l, boolean is) {level = l;isB = is;}}我們把代碼寫出來：
// process(head, 1)public static ReturnType process(Node head, int level) {if (head == null) {return new ReturnType(level, true);}//取信息ReturnType leftSubTreeInfo = process(head.left, level + 1);if(!leftSubTreeInfo.isB) {return new ReturnType(level, false); //左子樹不是->返回}ReturnType rightSubTreeInfo = process(head.right, level + 1);if(!rightSubTreeInfo.isB) {return new ReturnType(level, false); //右子樹不是->返回}if (Math.abs(rightSubTreeInfo.level - leftSubTreeInfo.level) > 1) {return new ReturnType(level, false); //左右高度差大于1->返回}return new ReturnType(Math.max(leftSubTreeInfo.level, rightSubTreeInfo.level), true);//返回高度和true（當前樹是平衡的）}我們不需要每次都返回高度，用一個全局變量記錄即可。
對于其它二叉樹問題，可能不止一個變量信息，所以，全局記錄最好都養成定義數組的習慣。
下面貼出完整代碼：
import java.util.LinkedList;
import java.util.Queue;public class Demo {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static boolean isBalance(Node head) {boolean[] res = new boolean[1];res[0] = true;getHeight(head, 1, res);return res[0];}public static class ReturnType {public int level; //深度public boolean isB;//本樹是否平衡public ReturnType(int l, boolean is) {level = l;isB = is;}}// process(head, 1)public static ReturnType process(Node head, int level) {if (head == null) {return new ReturnType(level, true);}//取信息ReturnType leftSubTreeInfo = process(head.left, level + 1);if(!leftSubTreeInfo.isB) {return new ReturnType(level, false); //左子樹不是->返回}ReturnType rightSubTreeInfo = process(head.right, level + 1);if(!rightSubTreeInfo.isB) {return new ReturnType(level, false); //右子樹不是->返回}if (Math.abs(rightSubTreeInfo.level - leftSubTreeInfo.level) > 1) {return new ReturnType(level, false); //左右高度差大于1->返回}return new ReturnType(Math.max(leftSubTreeInfo.level, rightSubTreeInfo.level), true);//返回高度和true（當前樹是平衡的}public static int getHeight(Node head, int level, boolean[] res) {if (head == null) {return level;//返回高度}//取信息//相同邏輯int lH = getHeight(head.left, level + 1, res);if (!res[0]) {return level;}int rH = getHeight(head.right, level + 1, res);if (!res[0]) {return level;}if (Math.abs(lH - rH) > 1) {res[0] = false;}return Math.max(lH, rH);//返回高度}public static void main(String[] args) {Node head = new Node(1);head.left = new Node(2);head.right = new Node(3);head.left.left = new Node(4);head.left.right = new Node(5);head.right.left = new Node(6);head.right.right = new Node(7);System.out.println(isBalance(head));}}判斷完全二叉樹
完全二叉樹的定義: 一棵二叉樹，除了最后一層之外都是完全填充的，并且最后一層的葉子結點都在左邊。
https://baike.baidu.com/item/%E5%AE%8C%E5%85%A8%E4%BA%8C%E5%8F%89%E6%A0%91/7773232?fr=aladdin
百度定義
?
思路：層序遍歷二叉樹
如果一個結點，左右孩子都不為空，則pop該節點，將其左右孩子入隊列
如果一個結點，左孩子為空，右孩子不為空，則該樹一定不是完全二叉樹
如果一個結點，左孩子不為空，右孩子為空；或者左右孩子都為空：：：：：則該節點之后的隊列中的結點都為葉子節點；該樹才是完全二叉樹，否則返回false。
非完全二叉樹的例子（對應方法的正確性和必要性）：
下面寫代碼：
定義結點：
public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}方法：
public static boolean isCBT(Node head) {if (head == null) {return true;}Queue<Node> queue = new LinkedList<Node>();boolean leaf = false;Node l = null;Node r = null;queue.offer(head);while (!queue.isEmpty()) {head = queue.poll();l = head.left;r = head.right;if ((leaf && (l != null || r != null)) || (l == null && r != null)) {return false;//當前結點不是葉子結點且之前結點有葉子結點 || 當前結點有右孩子無左孩子}if (l != null) {queue.offer(l);}if (r != null) {queue.offer(r);} else {leaf = true;//無孩子即為葉子結點}}return true;}判斷二叉搜索樹
二叉查找樹（Binary Search Tree），（又：二叉搜索樹，二叉排序樹）它或者是一棵空樹，或者是具有下列性質的二叉樹： 若它的左子樹不空，則左子樹上所有結點的值均小于它的根結點的值； 若它的右子樹不空，則右子樹上所有結點的值均大于它的根結點的值； 它的左、右子樹也分別為二叉排序樹。
?
判斷某棵樹是否為二叉搜索樹
?
單純判斷每個結點比左孩子大比右孩子小是不對的。如圖：
15推翻了這種方法。
?
思路：
1）可以根據定義判斷，遞歸進行，如果左右子樹都為搜索二叉樹，且左子樹最大值小于根，右子樹最小值大于根。成立。
2）根據定義，中序遍歷為遞增序列，我們中序遍歷后判斷是否遞增即可。
3）我們可以在中序遍歷過程中判斷之前節點和當前結點的關系，不符合直接返回false即可。
4）進一步通過morris遍歷優化
morris遍歷：https://blog.csdn.net/hebtu666/article/details/83093983
?
public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static boolean isBST(Node head) {if (head == null) {return true;}boolean res = true;Node pre = null;Node cur1 = head;Node cur2 = null;while (cur1 != null) {cur2 = cur1.left;if (cur2 != null) {while (cur2.right != null && cur2.right != cur1) {cur2 = cur2.right;}if (cur2.right == null) {cur2.right = cur1;cur1 = cur1.left;continue;} else {cur2.right = null;}}if (pre != null && pre.value > cur1.value) {res = false;}pre = cur1;cur1 = cur1.right;}return res;}二叉搜索樹實現
本文給出二叉搜索樹介紹和實現
?
首先說它的性質：所有的節點都滿足，左子樹上所有的節點都比自己小，右邊的都比自己大。
?
那這個結構有什么有用呢？
首先可以快速二分查找。還可以中序遍歷得到升序序列，等等。。。
基本操作：
1、插入某個數值
2、查詢是否包含某個數值
3、刪除某個數值
?
根據實現不同，還可以實現其他很多種操作。
?
實現思路思路：
前兩個操作很好想，就是不斷比較，大了往左走，小了往右走。到空了插入，或者到空都沒找到。
而刪除稍微復雜一些，有下面這幾種情況：
1、需要刪除的節點沒有左兒子，那就把右兒子提上去就好了。
2、需要刪除的節點有左兒子，這個左兒子沒有右兒子，那么就把左兒子提上去
3、以上都不滿足，就把左兒子子孫中最大節點提上來。
?
當然，反過來也是成立的，比如右兒子子孫中最小的節點。
?
下面來敘述為什么可以這么做。
下圖中A為待刪除節點。
第一種情況：
?
1、去掉A，把c提上來，c也是小于x的沒問題。
2、根據定義可知，x左邊的所有點都小于它，把c提上來不影響規則。
?
第二種情況
?
3、B<A<C,所以B<C,根據剛才的敘述，B可以提上去，c可以放在b右邊，不影響規則
4、同理
?
第三種情況
?
5、注意：是把黑色的提升上來，不是所謂的最右邊的那個，因為當初向左拐了，他一定小。
因為黑色是最大，比B以及B所有的孩子都大，所以讓B當左孩子沒問題
而黑點小于A，也就小于c，所以可以讓c當右孩子
大概證明就這樣。。
下面我們用代碼實現并通過注釋理解
上次鏈表之類的用的c，循環來寫的。這次就c++函數遞歸吧，不同方式練習。
定義
struct node
{int val;//數據node *lch,*rch;//左右孩子
};插入
node *insert(node *p,int x){if(p==NULL)//直到空就創建節點{node *q=new node;q->val=x;q->lch=q->rch=NULL;return p;}if(x<p->val)p->lch=insert(p->lch,x);else p->lch=insert(p->rch,x);return p;//依次返回自己，讓上一個函數執行。}查找
bool find(node *p,int x){if(p==NULL)return false;else if(x==p->val)return true;else if(x<p->val)return find(p->lch,x);else return find(p->rch,x);}刪除
node *remove(node *p,int x){if(p==NULL)return NULL;else if(x<p->val)p->lch=remove(p->lch,x);else if(x>p->val)p->lch=remove(p->rch,x);//以下為找到了之后else if(p->lch==NULL)//情況1{node *q=p->rch;delete p;return q;}else if(p->lch->rch)//情況2{node *q=p->lch;q->rch=p->rch;delete p;return q;}else{node *q;for(q=p->lch;q->rch->rch!=NULL;q=q->rch);//找到最大節點的前一個node *r=q->rch;//最大節點q->rch=r->lch;//最大節點左孩子提到最大節點位置r->lch=p->lch;//調整黑點左孩子為Br->rch=p->rch;//調整黑點右孩子為cdelete p;//刪除return r;//返回給父}return p;}堆的簡單實現
關于堆不做過多介紹
堆就是兒子的值一定不小于父親的值并且樹的節點都是按照從上到下，從左到右緊湊排列的樹。
（本文為二叉堆）
具體實現并不需要指針二叉樹，用數組儲存并且利用公式找到父子即可。
父：(i-1)/2
子:i*2+1,i*2+2
插入：首先把新數字放到堆的末尾，也就是右下角，然后查看父的數值，需要交換就交換，重復上述操作直到不需交換
刪除：把堆的第一個節點賦值為最后一個節點的值，然后刪除最后一個節點，不斷向下交換。
（兩個兒子：嚴格來說要選擇數值較小的那一個）
時間復雜度：和深度成正比，所以n個節點是O(logN)
int heap[MAX_N],sz=0;
//定義數組和記錄個數的變量插入代碼：
void push(int x)
{//節點編號int i=sz++;while(i>0){int p=(i-1)/2;//父if(heap[p]<=x)break;//直到大小順序正確跳出循環heap[i]=heap[p];//把父節點放下來i=p;}heap[i]=x;//最后把自己放上去}彈出：
int pop()
{int ret=heap[0];//保存好值，最后返回int x=heap[--sz];while(i*2+1<sz){int a=i*2+1;//左孩子int b=i*2+2;//右孩子if(b<sz && heap[b]<heap[a])a=b;//找最小if(heap[a]>=x)break;//直到不需要交換就退出heap[i]=heap[a];//把兒子放上來i=a;}head[i]=x;//下沉到正確位置return ret;//返回
}堆應用例題三連
一個數據流中，隨時可以取得中位數。
題目描述：有一個源源不斷地吐出整數的數據流，假設你有足夠的空間來保存吐出的數。請設計一個名叫MedianHolder的結構，MedianHolder可以隨時取得之前吐出所有樹的中位數。
要求：
1.如果MedianHolder已經保存了吐出的N個數，那么任意時刻將一個新的數加入到MedianHolder的過程中，時間復雜度O(logN)。
2.取得已經吐出的N個數整體的中位數的過程，時間復雜度O(1).
?
看這要求就應該感覺到和堆相關吧？
但是進一步沒那么好想。
設計的MedianHolder中有兩個堆，一個是大根堆，一個是小根堆。大根堆中含有接收的所有數中較小的一半，并且按大根堆的方式組織起來，那么這個堆的堆頂就是較小一半的數中最大的那個。小根堆中含有接收的所有數中較大的一半，并且按小根堆的方式組織起來，那么這個堆的堆頂就是較大一半的數中最小的那個。
例如，如果已經吐出的數為6,1,3,0,9,8,7,2.
較小的一半為：0,1,2,3，那么3就是這一半的數組成的大根堆的堆頂
較大的一半為：6,7,8,9，那么6就是這一半的數組成的小根堆的堆頂
因為此時數的總個數為偶數，所以中位數就是兩個堆頂相加，再除以2.
如果此時新加入一個數10，那么這個數應該放進較大的一半里，所以此時較大的一半數為6,7,8,9,10，此時6依然是這一半的數組成的小根堆的堆頂，因為此時數的總個數為奇數，所以中位數應該是正好處在中間位置的數，而此時大根堆有4個數，小根堆有5個數，那么小根堆的堆頂6就是此時的中位數。
如果此時又新加入一個數11，那么這個數也應該放進較大的一半里，此時較大一半的數為：6,7,8,9,10,11.這個小根堆大小為6，而大根堆的大小為4，所以要進行如下調整：
1.如果大根堆的size比小根堆的size大2，那么從大根堆里將堆頂元素彈出，并放入小根堆里
2，如果小根堆的size比大根堆的size大2，那么從小根堆里將堆頂彈出，并放入大根堆里。
經過這樣的調整之后，大根堆和小根堆的size相同。
總結如下：
大根堆每時每刻都是較小的一半的數，堆頂為這一堆數的最大值
小根堆每時每刻都是較大的一半的數，堆頂為這一堆數的最小值
新加入的數根據與兩個堆堆頂的大小關系，選擇放進大根堆或者小根堆里（或者放進任意一個堆里）
當任何一個堆的size比另一個size大2時，進行如上調整的過程。
這樣隨時都可以知道已經吐出的所有數處于中間位置的兩個數是什么，取得中位數的操作時間復雜度為O(1)，同時根據堆的性質，向堆中加一個新的數，并且調整堆的代價為O（logN）。
?
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;/*** 隨時找到數據流的中位數* 思路：* 利用一個大根堆和一個小根堆去保存數據，保證前一半的數放在大根堆，后一半的數放在小根堆* 在添加數據的時候，不斷地調整兩個堆的大小，使得兩個堆保持平衡* 要取得的中位數就是兩個堆堆頂的元素*/
public class MedianQuick {public static class MedianHolder {private PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(new MaxHeapComparator());private PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>(new MinHeapComparator());/*** 調整堆的大小* 當兩個堆的大小差值變大時，從數據多的堆中彈出一個數據進入另一個堆中*/private void modifyTwoHeapsSize() {if (this.maxHeap.size() == this.minHeap.size() + 2) {this.minHeap.add(this.maxHeap.poll());}if (this.minHeap.size() == this.maxHeap.size() + 2) {this.maxHeap.add(this.minHeap.poll());}}/*** 添加數據的過程** @param num*/public void addNumber(int num) {if (this.maxHeap.isEmpty()) {this.maxHeap.add(num);return;}if (this.maxHeap.peek() >= num) {this.maxHeap.add(num);} else {if (this.minHeap.isEmpty()) {this.minHeap.add(num);return;}if (this.minHeap.peek() > num) {this.maxHeap.add(num);} else {this.minHeap.add(num);}}modifyTwoHeapsSize();}/*** 獲取中位數** @return*/public Integer getMedian() {int maxHeapSize = this.maxHeap.size();int minHeapSize = this.minHeap.size();if (maxHeapSize + minHeapSize == 0) {return null;}Integer maxHeapHead = this.maxHeap.peek();Integer minHeapHead = this.minHeap.peek();if (((maxHeapSize + minHeapSize) & 1) == 0) {return (maxHeapHead + minHeapHead) / 2;}return maxHeapSize > minHeapSize ? maxHeapHead : minHeapHead;}}/*** 大根堆比較器*/public static class MaxHeapComparator implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {if (o2 > o1) {return 1;} else {return -1;}}}/*** 小根堆比較器*/public static class MinHeapComparator implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {if (o2 < o1) {return 1;} else {return -1;}}}// for testpublic static int[] getRandomArray(int maxLen, int maxValue) {int[] res = new int[(int) (Math.random() * maxLen) + 1];for (int i = 0; i != res.length; i++) {res[i] = (int) (Math.random() * maxValue);}return res;}// for test, this method is ineffective but absolutely rightpublic static int getMedianOfArray(int[] arr) {int[] newArr = Arrays.copyOf(arr, arr.length);Arrays.sort(newArr);int mid = (newArr.length - 1) / 2;if ((newArr.length & 1) == 0) {return (newArr[mid] + newArr[mid + 1]) / 2;} else {return newArr[mid];}}public static void printArray(int[] arr) {for (int i = 0; i != arr.length; i++) {System.out.print(arr[i] + " ");}System.out.println();}public static void main(String[] args) {boolean err = false;int testTimes = 200000;for (int i = 0; i != testTimes; i++) {int len = 30;int maxValue = 1000;int[] arr = getRandomArray(len, maxValue);MedianHolder medianHold = new MedianHolder();for (int j = 0; j != arr.length; j++) {medianHold.addNumber(arr[j]);}if (medianHold.getMedian() != getMedianOfArray(arr)) {err = true;printArray(arr);break;}}System.out.println(err ? "Oops..what a fuck!" : "today is a beautiful day^_^");}
}
金條
?
一塊金條切成兩半，是需要花費和長度數值一樣的銅板的。比如長度為20的金條，不管切成長度多大的兩半，都要花費20個銅板。一群人想整分整塊金條，怎么分最省銅板？
例如，給定數組{10,20,30},代表一共三個人，整塊金條長度為10+20+30=60，金條要分成10,20,30三個部分。如果，先把長度60的金條分成10和50，花費60，再把長度為50的金條分成20和30，花費50，一共花費110個銅板。
但是如果，先把長度60的金條分成30和30，花費60，再把長度30金條分成10和30，花費30，一共花費90個銅板。
輸入一個數組，返回分割的最小代價。
首先我們要明白一點：不管合并策略是什么我們一共會合并n-1次，這個次數是不會變的。
我們要做的就是每一次都做最優選擇。
合為最優？
最小的兩個數合并就是最優。
所以
1）首先構造小根堆
2）每次取最小的兩個數（小根堆），使其代價最小。并將其和加入到小根堆中
3）重復（2）過程，直到最后堆中只剩下一個節點。
?
花費為每次花費的累加。
代碼略。
?
項目最大收益（貪心問題）
輸入：參數1，正數數組costs，參數2，正數數組profits，參數3，正數k，參數4，正數m
costs[i]表示i號項目的花費profits[i]表示i號項目在扣除花費之后還能掙到的錢（利潤）,k表示你不能并行，只能串行的最多做k個項目，m表示你初始的資金。
說明：你每做完一個項目，馬上獲得的收益，可以支持你去做下一個項目。
輸出：你最后獲得的最大錢數。
思考：給定一個初始化投資資金，給定N個項目，想要獲得其中最大的收益，并且一次只能做一個項目。這是一個貪心策略的問題，應該在能做的項目中選擇收益最大的。
按照花費的多少放到一個小根堆里面，然后要是小根堆里面的頭節點的花費少于給定資金，就將頭節點一個個取出來，放到按照收益的大根堆里面。然后做大根堆頂的項目即可。
?并查集實現
并查集是什么東西？
它是用來管理元素分組情況的一種數據結構。
他可以高效進行兩個操作：
- 查詢a，b是否在同一組
- 合并a和b所在的組
萌新可能不知所云，這個結構到底有什么用？
經分析，并查集效率之高超乎想象，對n個元素的并查集進行一次操作的復雜度低于O(logn)
?
我們先說并查集是如何實現的：
也是使用樹形結構，但不是二叉樹。
每個元素就是一個結點，每組都是一個樹。
無需關注它的形狀，或哪個節點具體在哪個位置。
?
初始化：
我們現在有n個結點，也就是n個元素。
?
合并：
然后我們就可以合并了，合并方法就是把一個根放到另一顆樹的下面，也就是整棵樹作為人家的一個子樹。
?
查詢：
查詢兩個結點是否是同一組，需要知道這兩個結點是不是在一棵樹上，讓他們分別沿著樹向根找，如果兩個元素最后走到一個根，他們就在一組。
?
當然，樹形結構都存在退化的缺點，對于每種結構，我們都有自己的優化方法，下面我們說明如何避免退化。
- 記錄每一棵樹的高度，合并操作時，高度小的變為高度大的子樹即可。
- 路徑壓縮：對于一個節點，只要走到了根節點，就不必再在很深的地方，直接改為連著根即可。進一步優化：其實每一個經過的節點都可以直接連根。
這樣查詢的時候就能很快地知道根是誰了。
?
下面上代碼實現：
和很多樹結構一樣，我們沒必要真的模擬出來，數組中即可。
int p[MAX_N];//父親
int rank[MAX_N];//高度
//初始化
void gg(int n)
{for(int i=0;i<n;i++){p[i]=i;//父是自己代表是根rank[i]=0;}
}
//查詢根
int find(int x)
{if(p[x]==x)return x;return p[x]=find(p[x])//不斷把經過的結點連在根
}
//判斷是否屬于同一組
bool judge(int x,int y)
{return find(x)==find(y);//查詢結果一樣就在一組
}
//合并
void unite(int x,int y)
{if(x==y)return;if(rank[x]<rank[y])p[x]=y;//深度小，放在大的下面else{p[y]=x;if(rank[x]=rank[y])rank[x]++;//一樣，y放x后，x深度加一}
}實現很簡單，應用有難度，以后有時間更新題。
并查集入門三連：HDU1213 POJ1611 POJ2236
HDU1213
http://acm.hdu.edu.cn/showproblem.php?pid=1213
問題描述
今天是伊格納修斯的生日。他邀請了很多朋友。現在是晚餐時間。伊格納修斯想知道他至少需要多少桌子。你必須注意到并非所有的朋友都互相認識，而且所有的朋友都不想和陌生人呆在一起。
這個問題的一個重要規則是，如果我告訴你A知道B，B知道C，那意味著A，B，C彼此了解，所以他們可以留在一個表中。
例如：如果我告訴你A知道B，B知道C，D知道E，所以A，B，C可以留在一個表中，D，E必須留在另一個表中。所以Ignatius至少需要2張桌子。
輸入
輸入以整數T（1 <= T <= 25）開始，表示測試用例的數量。然后是T測試案例。每個測試用例以兩個整數N和M開始（1 <= N，M <= 1000）。N表示朋友的數量，朋友從1到N標記。然后M行跟隨。每一行由兩個整數A和B（A！= B）組成，這意味著朋友A和朋友B彼此了解。兩個案例之間會有一個空白行。
?
對于每個測試用例，只輸出Ignatius至少需要多少個表。不要打印任何空白。
樣本輸入
2
5 3
1 2
2 3
4 5
?
5 1
2 5
樣本輸出
2
4
并查集基礎題
#include<cstdio>
#include<iostream>
using namespace std;
int fa[1005];
int n,m;
void init()//初始化
{for(int i=0;i<1005;i++)fa[i]=i;
}
int find(int x)//尋根
{if(fa[x]!=x)fa[x]=find(fa[x]);return fa[x];
}
void union(int x,int y)//判斷、合并
{int a=find(x),b=find(y);if(a!=b)fa[b]=a;
}
int main()
{int t;scanf("%d",&t);while(t--){int a,b,cnt=0;scanf("%d%d",&n,&m);init();for(int i=1;i<=m;i++)//合并{scanf("%d%d",&a,&b);union(a,b);}for(int i=1;i<=n;i++)//統計{find(i);if(find(i)==i)cnt++;}printf("%d\n",cnt);}return 0;
}
POJ1611
http://poj.org/problem?id=1611
描述
嚴重急性呼吸系統綜合癥（SARS）是一種病因不明的非典型肺炎，在2003年3月中旬被認為是一種全球性威脅。為了盡量減少對他人的傳播，最好的策略是將嫌疑人與其他嫌疑人分開。?
在Not-Spreading-Your-Sickness University（NSYSU），有許多學生團體。同一組中的學生經常互相交流，學生可以加入幾個小組。為了防止可能的SARS傳播，NSYSU收集所有學生組的成員列表，并在其標準操作程序（SOP）中制定以下規則。?
一旦組中的成員是嫌疑人，該組中的所有成員都是嫌疑人。?
然而，他們發現，當學生被認定為嫌疑人時，識別所有嫌疑人并不容易。你的工作是編寫一個找到所有嫌疑人的程序。
輸入
輸入文件包含幾種情況。每個測試用例以一行中的兩個整數n和m開始，其中n是學生數，m是組的數量。您可以假設0 <n <= 30000且0 <= m <= 500.每個學生都使用0到n-1之間的唯一整數進行編號，并且最初學生0在所有情況下都被識別為嫌疑人。該行后面是組的m個成員列表，每組一行。每行以整數k開頭，表示組中的成員數。在成員數量之后，有k個整數代表該組中的學生。一行中的所有整數由至少一個空格分隔。?
n = 0且m = 0的情況表示輸入結束，無需處理。
?
對于每種情況，輸出一行中的嫌疑人數量。
樣本輸入
100 4
2 1 2
5 10 13 11 12 14
2 0 1
2 99 2
200 2
1 5
5 1 2 3 4 5
1 0
0 0樣本輸出
4
1
1?
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include <string>
using namespace std;
int a[30001],pre[30001];
int find(int x)//尋根
{if(pre[x]==x)return x;elsereturn pre[x]=find(pre[x]);
}
void union(int x, int y)//合并
{int fx = find(x), fy = find(y);if (fx != fy)pre[fy] = fx;
}int main()
{int n,m;while (scanf("%d%d", &n, &m) != EOF && (n || m)){int sum = 0;for (int i = 0; i < n; i++)//初始化pre[i] = i;for (int i = 0; i < m; i++){int k;scanf("%d", &k);if (k >= 1){scanf("%d", &a[0]);for (int j = 1; j < k; j++){scanf("%d", &a[j]);//接收union(a[0], a[j]);//和0號一組}}}for (int i = 0; i < n; i++)//統計if (find(i) ==pre[0])sum++;printf("%d\n", sum);}return 0;
}
?POJ2236
http://poj.org/problem?id=2236
描述
地震發生在東南亞。ACM（亞洲合作醫療團隊）已經與膝上電腦建立了無線網絡，但是一次意外的余震襲擊，網絡中的所有計算機都被打破了。計算機一個接一個地修復，網絡逐漸開始工作。由于硬件限制，每臺計算機只能直接與距離它不遠的計算機進行通信。但是，每臺計算機都可以被視為兩臺計算機之間通信的中介，也就是說，如果計算機A和計算機B可以直接通信，或者計算機C可以與A和A進行通信，則計算機A和計算機B可以進行通信。 B.?
在修復網絡的過程中，工作人員可以隨時進行兩種操作，修復計算機或測試兩臺計算機是否可以通信。你的工作是回答所有的測試操作。?
輸入
第一行包含兩個整數N和d（1 <= N <= 1001,0 <= d <= 20000）。這里N是計算機的數量，編號從1到N，D是兩臺計算機可以直接通信的最大距離。在接下來的N行中，每行包含兩個整數xi，yi（0 <= xi，yi <= 10000），這是N臺計算機的坐標。從第（N + 1）行到輸入結束，有一些操作，這些操作是一個接一個地執行的。每行包含以下兩種格式之一的操作：?
1。“O p”（1 <= p <= N），表示修復計算機p。?
2.“S p q”（1 <= p，q <= N），這意味著測試計算機p和q是否可以通信。?
輸入不會超過300000行。?
產量
對于每個測試操作，如果兩臺計算機可以通信則打印“SUCCESS”，否則打印“FAIL”。
樣本輸入
4 1
0 1
0 2
0 3
0 4
O 1
O 2
O 4
S 1 4
O 3
S 1 4樣本輸出
FAIL
SUCCESS?思路：對每次修好的電腦對其它已經修好的電腦遍歷，如果距離小于等于最大通信距離就將他們合并。
注意：
1、坐標之后給出的計算機編號都是n+1的。例如O 3，他實際上修理的是編號為2的計算機，因為計算機是從0開始編號的。
2、比較距離的時候注意要用浮點數比較，否則會WA。
3、"FAIL"不要寫成"FALL"。
4、字符串輸入的時候注意處理好回車，空格等情況。
5、注意N的范圍（1 <= N <= 1001），最大是1001，不是1000。是個小坑，數組開小了可能會錯哦。
?
#include <iostream>
#include <stdio.h>
#include <cmath>
using namespace std;#define MAXN 1010int dx[MAXN],dy[MAXN]; //坐標
int par[MAXN]; //x的父節點
int repair[MAXN] ={0};
int n;void Init()//初始化
{int i;for(i=0;i<=n;i++)par[i] = i;
}int Find(int x)//尋根
{if(par[x]!=x)par[x] = Find(par[x]);return par[x];
}void Union(int x,int y)//合并
{par[Find(x)] = Find(y);
}int Abs(int n)//絕對值
{return n>0?n:-n;
}double Dis(int a,int b)//坐標
{return sqrt( double(dx[a]-dx[b])*(dx[a]-dx[b]) + (dy[a]-dy[b])*(dy[a]-dy[b]) );
}int main()
{int d,i;//初始化scanf("%d%d",&n,&d);Init();//輸入坐標for(i=0;i<n;i++){scanf("%d%d",&dx[i],&dy[i]);}//操作char cmd[2];int p,q,len=0;while(scanf("%s",cmd)!=EOF){switch(cmd[0]){case 'O':scanf("%d",&p);p--;repair[len++] = p;for(i=0;i<len-1;i++) //遍歷所有修過的計算機，看能否聯通if( repair[i]!=p && Dis(repair[i],p)<=double(d) )Union(repair[i],p);break;case 'S':scanf("%d%d",&p,&q);p--,q--;if(Find(p)==Find(q)) //判斷printf("SUCCESS\n");else printf("FAIL\n");default:break;}}return 0;
}線段樹簡單實現
首先，線段樹是一棵滿二叉樹。（每個節點要么有兩個孩子，要么是深度相同的葉子節點）
每個節點維護某個區間，根維護所有的。
?轉存失敗重新上傳取消?
如圖，區間是二分父的區間。
當有n個元素，初始化需要o(n)時間，對區間操作需要o(logn)時間。
下面給出維護區間最小值的思路和代碼
功能：一樣的，依舊是查詢和改值。
查詢[s,t]之間最小的數。修改某個值。
?
從下往上，每個節點的值為左右區間較小的那一個即可。
這算是簡單動態規劃思想，做到了o(n)，因為每個節點就訪問一遍，而葉子節點一共n個，所以訪問2n次即可。
如果利用深搜初始化，會到o(nlogn)。
https://blog.csdn.net/hebtu666/article/details/81777273
有介紹
那我們繼續說，如何查詢。
不要以為它是二分區間就只能查二分的那些區間，它能查任意區間。
比如上圖，求1-7的最小值，查詢1-4，5-6，7-7即可。
下面說過程：
遞歸實現：
如果要查詢的區間和本節點區間沒有重合，返回一個特別大的數即可，不要影響其他結果。
如果要查詢的區間完全包含了本節點區間，返回自身的值
都不滿足，對左右兒子做遞歸，返回較小的值。
?
如何更新？
更新ai，就要更新所有包含ai的區間。
可以從下往上不斷更新，把節點的值更新為左右孩子較小的即可。
?
代碼實現和相關注釋：
注：沒有具體的初始化，dp思路寫過了，實在不想寫了
初始全為INT_MAX
const int MAX_N=1<<7;
int n;
int tree[2*MAX_N-1];
//初始化
void gg(int nn)
{n=1;while(n<nn)n*=2;//把元素個數變為2的n次方for(int i=0;i<2*n-1;i++)tree[i]=INTMAX;//所有值初始化為INTMAX
}//查詢區間最小值
int get(int a,int b,int k,int l,int r)//l和r是區間，k是節點下標，求[a,b)最小值
{if(a>=r || b<=l)return INTMAX;//情況1if(a<=l || b<=b)return tree[k];//情況2int ll=get(a,b,k*2+1,l,(l+r)/2);//以前寫過，左孩子公式int rr=get(a,b,k*2+2,(l+r)/2,r);//右孩子return min(ll,rr);
}//更新
void update(int k,int a)//第k個值更新為a
{//本身k+=n-1;//加上前面一堆節點數tree[k]=a;//開始向上while(k>0){tree[k]=min(tree[2*k+1],tree[2*k+2]);k=(k-1)/2//父的公式，也寫過}
}?樹狀數組實現
樹狀數組能夠完成如下操作：
給一個序列a0-an
計算前i項和
對某個值加x
時間o(logn)
?
注意：有人覺得前綴和就行了，但是你還要維護啊，改變某個值，一個一個改變前綴和就是o(n)了。
線段樹樹狀數組的題就是這樣，維護一個樹，比較容易看出來。
?
?
線段樹：
https://blog.csdn.net/hebtu666/article/details/82691008
如果使用線段樹，只需要對網址中的實現稍微修改即可。以前維護最小值，現在維護和而已。
注意：要求只是求出前i項，而并未給定一個區間，那我們就能想出更快速、方便的方法。
對于任意一個節點，作為右孩子，如果求和時被用到，那它的左兄弟一定也會被用到，那我們就沒必要再用右孩子，因為用他們的父就可以了。
這樣一來，我們就可以把所有有孩子全部去掉
把剩下的節點編號。
?轉存失敗重新上傳取消?
如圖，可以發現一些規律：1，3，5，7，9等奇數，區間長度都為1
6，10，14等長度為2
........................
如果我們吧編號換成二進制，就能發現，二進制以1結尾的數字區間長度為1，最后有一個零的區間為2，兩個零的區間為4.
我們利用二進制就能很容易地把編號和區間對應起來。
?
計算前i項和。
需要把當前編號i的數值加進來，把i最右邊的1減掉，直到i變為0.
二進制最后一個1可以通過i&-i得到。
?
更新：
不斷把當前位置i加x，把i的二進制最低非零位對應的冪加到i上。
下面是代碼：
思想想出來挺麻煩，代碼實現很簡單，我都不知道要注釋點啥
向發明這些東西的大佬們致敬
int bit[MAX_N+1]
int n;int sum(int i)
{int gg=0;while(i>0){gg+=bit[i];i-=i&-i;}return gg;
}void add(int i,int x)
{while(i<=n){bit[i]+=x;i+=i&-i;}
}最大搜索子樹
給定一個二叉樹的頭結點，返回最大搜索子樹的大小。
?
我們先定義結點：
public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}分析：
直接判斷每個節點左邊小右邊大是不對滴
?
可以暴力判斷所有的子樹，就不說了。
?
最大搜索子樹可能性：
第一種可能性，以node為頭的結點的最大二叉搜索子樹可能來自它左子樹；
第二種可能性，以node為頭的結點的最大二叉搜索子樹可能來自它右子樹；
第三種可能性，左樹整體是搜索二叉樹，右樹整體也是搜索二叉樹，而且左樹的頭是node.left，右樹的頭是node.right，且左樹的最大值< node.value，右樹的最小值 > node.value， 那么以我為頭的整棵樹都是搜索二叉樹；
?
第三種可能性的判斷，需要的信息有：左子樹的最大值、右子樹的最小值、左子樹是不是搜索二叉樹、右子樹是不是搜索二叉樹
還有左右搜索二叉樹的最大深度。
我們判斷了自己，并不知道自己是哪邊的子樹，我們要返回自己的最大值和最小值。
這樣，定義一個返回類型：
public static class ReturnType{public int size;//最大搜索子樹深度public Node head;//最大搜索子樹的根public int min;//子樹最小public int max;//子樹最大public ReturnType(int a, Node b,int c,int d) {this.size =a;this.head = b;this.min = c;this.max = d;}}然后開始寫代碼：
注意：
1）NULL返回深度0，頭為NULL，最大值最小值返回系統最大和最小，這樣才不會影響別的判斷。
public static ReturnType process(Node head) {if(head == null) {return new ReturnType(0,null,Integer.MAX_VALUE, Integer.MIN_VALUE);}Node left = head.left;//取信息ReturnType leftSubTressInfo = process(left);Node right = head.right;ReturnType rightSubTressInfo = process(right);int includeItSelf = 0;if(leftSubTressInfo.head == left // 左子樹為搜索樹&&rightSubTressInfo.head == right// 右子樹為搜索樹&& head.value > leftSubTressInfo.max// 左子樹最大值小于當前節點&& head.value < rightSubTressInfo.min//右子樹最小值大于當前節點) {includeItSelf = leftSubTressInfo.size + 1 + rightSubTressInfo.size;//當前節點為根的二叉樹為搜索樹}int p1 = leftSubTressInfo.size;int p2 = rightSubTressInfo.size;int maxSize = Math.max(Math.max(p1, p2), includeItSelf);//最大搜索樹深度Node maxHead = p1 > p2 ? leftSubTressInfo.head : rightSubTressInfo.head;if(maxSize == includeItSelf) {maxHead = head;}//最大搜索樹的根：來自左子樹、來自右子樹、本身return new ReturnType(maxSize, //深度maxHead, //根Math.min(Math.min(leftSubTressInfo.min,rightSubTressInfo.min),head.value), //最小Math.max(Math.max(leftSubTressInfo.max,rightSubTressInfo.max),head.value)); //最大}可以進一步改進：
空間浪費比較嚴重
其實返回值為三個int，一個node，我們可以把三個int合起來，用全局數組記錄，函數只返回node（搜索樹的根）即可。
給出完整代碼：
public class BiggestSubBSTInTree {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static Node biggestSubBST(Node head) {int[] record = new int[3]; // 0->size, 1->min, 2->maxreturn posOrder(head, record);}public static class ReturnType{public int size;//最大搜索子樹深度public Node head;//最大搜索子樹的根public int min;//子樹最小public int max;//子樹最大public ReturnType(int a, Node b,int c,int d) {this.size =a;this.head = b;this.min = c;this.max = d;}}public static ReturnType process(Node head) {if(head == null) {return new ReturnType(0,null,Integer.MAX_VALUE, Integer.MIN_VALUE);}Node left = head.left;//取信息ReturnType leftSubTressInfo = process(left);Node right = head.right;ReturnType rightSubTressInfo = process(right);int includeItSelf = 0;if(leftSubTressInfo.head == left // 左子樹為搜索樹&&rightSubTressInfo.head == right// 右子樹為搜索樹&& head.value > leftSubTressInfo.max// 左子樹最大值小于當前節點&& head.value < rightSubTressInfo.min//右子樹最小值大于當前節點) {includeItSelf = leftSubTressInfo.size + 1 + rightSubTressInfo.size;//當前節點為根的二叉樹為搜索樹}int p1 = leftSubTressInfo.size;int p2 = rightSubTressInfo.size;int maxSize = Math.max(Math.max(p1, p2), includeItSelf);//最大搜索樹深度Node maxHead = p1 > p2 ? leftSubTressInfo.head : rightSubTressInfo.head;if(maxSize == includeItSelf) {maxHead = head;}//最大搜索樹的根：來自左子樹、來自右子樹、本身return new ReturnType(maxSize, //深度maxHead, //根Math.min(Math.min(leftSubTressInfo.min,rightSubTressInfo.min),head.value), //最小Math.max(Math.max(leftSubTressInfo.max,rightSubTressInfo.max),head.value)); //最大}public static Node posOrder(Node head, int[] record) {if (head == null) {record[0] = 0;record[1] = Integer.MAX_VALUE;record[2] = Integer.MIN_VALUE;return null;}int value = head.value;Node left = head.left;Node right = head.right;Node lBST = posOrder(left, record);int lSize = record[0];int lMin = record[1];int lMax = record[2];Node rBST = posOrder(right, record);int rSize = record[0];int rMin = record[1];int rMax = record[2];record[1] = Math.min(rMin, Math.min(lMin, value)); // lmin, value, rmin -> min record[2] = Math.max(lMax, Math.max(rMax, value)); // lmax, value, rmax -> maxif (left == lBST && right == rBST && lMax < value && value < rMin) {record[0] = lSize + rSize + 1;//修改深度return head; //返回根}//滿足當前構成搜索樹的條件record[0] = Math.max(lSize, rSize);//較大深度return lSize > rSize ? lBST : rBST;//返回較大搜索樹的根}// for test -- print treepublic static void printTree(Node head) {System.out.println("Binary Tree:");printInOrder(head, 0, "H", 17);System.out.println();}public static void printInOrder(Node head, int height, String to, int len) {if (head == null) {return;}printInOrder(head.right, height + 1, "v", len);String val = to + head.value + to;int lenM = val.length();int lenL = (len - lenM) / 2;int lenR = len - lenM - lenL;val = getSpace(lenL) + val + getSpace(lenR);System.out.println(getSpace(height * len) + val);printInOrder(head.left, height + 1, "^", len);}public static String getSpace(int num) {String space = " ";StringBuffer buf = new StringBuffer("");for (int i = 0; i < num; i++) {buf.append(space);}return buf.toString();}public static void main(String[] args) {Node head = new Node(6);head.left = new Node(1);head.left.left = new Node(0);head.left.right = new Node(3);head.right = new Node(12);head.right.left = new Node(10);head.right.left.left = new Node(4);head.right.left.left.left = new Node(2);head.right.left.left.right = new Node(5);head.right.left.right = new Node(14);head.right.left.right.left = new Node(11);head.right.left.right.right = new Node(15);head.right.right = new Node(13);head.right.right.left = new Node(20);head.right.right.right = new Node(16);printTree(head);Node bst = biggestSubBST(head);printTree(bst);}}
morris遍歷
通常，實現二叉樹的前序（preorder）、中序（inorder）、后序（postorder）遍歷有兩個常用的方法：一是遞歸(recursive)，二是使用棧實現的迭代版本(stack+iterative)。這兩種方法都是O(n)的空間復雜度（遞歸本身占用stack空間或者用戶自定義的stack）。
本文介紹空間O(1)的遍歷方法。
上次文章講到，我們經典遞歸遍歷其實有三次訪問當前節點的機會，就看你再哪次進行操作，而分成了三種遍歷。
https://blog.csdn.net/hebtu666/article/details/82853988
morris有兩次訪問節點的機會。
它省空間的原理是利用了大量葉子節點的沒有用的空間，記錄之前的節點，做到了返回之前節點這件事情。
我們不說先序中序后序，先說morris遍歷的原則：
1、如果沒有左孩子，繼續遍歷右子樹
2、如果有左孩子，找到左子樹最右節點。
? ? 1）如果最右節點的右指針為空（說明第一次遇到），把它指向當前節點，當前節點向左繼續處理。
? ? 2）如果最右節點的右指針不為空（說明它指向之前結點），把右指針設為空，當前節點向右繼續處理。
?
這就是morris遍歷。
請手動模擬深度至少為3的樹的morris遍歷來熟悉流程。
?
先看代碼：
定義結點：
public static class Node {public int value;Node left;Node right;public Node(int data) {this.value = data;}}先序：
?（完全按規則寫就好。）
//打印時機（第一次遇到）：發現左子樹最右的孩子右指針指向空，或無左子樹。public static void morrisPre(Node head) {if (head == null) {return;}Node cur1 = head;Node cur2 = null;while (cur1 != null) {cur2 = cur1.left;if (cur2 != null) {while (cur2.right != null && cur2.right != cur1) {cur2 = cur2.right;}if (cur2.right == null) {cur2.right = cur1;System.out.print(cur1.value + " ");cur1 = cur1.left;continue;} else {cur2.right = null;}} else {System.out.print(cur1.value + " ");}cur1 = cur1.right;}System.out.println();}morris在發表文章時只寫出了中序遍歷。而先序遍歷只是打印時機不同而已，所以后人改進出了先序遍歷。至于后序，是通過打印所有的右邊界來實現的：對每個有邊界逆序，打印，再逆序回去。注意要原地逆序，否則我們morris遍歷的意義也就沒有了。
完整代碼：?
public class MorrisTraversal {public static void process(Node head) {if(head == null) {return;}// 1//System.out.println(head.value);process(head.left);// 2//System.out.println(head.value);process(head.right);// 3//System.out.println(head.value);}public static class Node {public int value;Node left;Node right;public Node(int data) {this.value = data;}}
//打印時機：向右走之前public static void morrisIn(Node head) {if (head == null) {return;}Node cur1 = head;//當前節點Node cur2 = null;//最右while (cur1 != null) {cur2 = cur1.left;//左孩子不為空if (cur2 != null) {while (cur2.right != null && cur2.right != cur1) {cur2 = cur2.right;}//找到最右//右指針為空，指向cur1，cur1向左繼續if (cur2.right == null) {cur2.right = cur1;cur1 = cur1.left;continue;} else {cur2.right = null;}//右指針不為空，設為空}System.out.print(cur1.value + " ");cur1 = cur1.right;}System.out.println();}
//打印時機（第一次遇到）：發現左子樹最右的孩子右指針指向空，或無左子樹。public static void morrisPre(Node head) {if (head == null) {return;}Node cur1 = head;Node cur2 = null;while (cur1 != null) {cur2 = cur1.left;if (cur2 != null) {while (cur2.right != null && cur2.right != cur1) {cur2 = cur2.right;}if (cur2.right == null) {cur2.right = cur1;System.out.print(cur1.value + " ");cur1 = cur1.left;continue;} else {cur2.right = null;}} else {System.out.print(cur1.value + " ");}cur1 = cur1.right;}System.out.println();}
//逆序打印所有右邊界public static void morrisPos(Node head) {if (head == null) {return;}Node cur1 = head;Node cur2 = null;while (cur1 != null) {cur2 = cur1.left;if (cur2 != null) {while (cur2.right != null && cur2.right != cur1) {cur2 = cur2.right;}if (cur2.right == null) {cur2.right = cur1;cur1 = cur1.left;continue;} else {cur2.right = null;printEdge(cur1.left);}}cur1 = cur1.right;}printEdge(head);System.out.println();}
//逆序打印public static void printEdge(Node head) {Node tail = reverseEdge(head);Node cur = tail;while (cur != null) {System.out.print(cur.value + " ");cur = cur.right;}reverseEdge(tail);}
//逆序（類似鏈表逆序）public static Node reverseEdge(Node from) {Node pre = null;Node next = null;while (from != null) {next = from.right;from.right = pre;pre = from;from = next;}return pre;}public static void main(String[] args) {Node head = new Node(4);head.left = new Node(2);head.right = new Node(6);head.left.left = new Node(1);head.left.right = new Node(3);head.right.left = new Node(5);head.right.right = new Node(7);morrisIn(head);morrisPre(head);morrisPos(head);}}最小生成樹
?
問題提出：
????要在n個城市間建立通信聯絡網。頂點：表示城市，權：城市間通信線路的花費代價。希望此通信網花費代價最小。
問題分析：
????答案只能從生成樹中找，因為要做到任何兩個城市之間有線路可達，通信網必須是連通的；但對長度最小的要求可以知道網中顯然不能有圈，如果有圈，去掉一條邊后，并不破壞連通性，但總代價顯然減少了，這與總代價最小的假設是矛盾的。
結論：
????希望找到一棵生成樹，它的每條邊上的權值之和（即建立該通信網所需花費的總代價）最小 —— 最小代價生成樹。
????構造最小生成樹的算法很多，其中多數算法都利用了一種稱之為 MST 的性質。
????MST 性質：設 N = (V, E) ?是一個連通網，U是頂點集 V的一個非空子集。若邊 (u, v) 是一條具有最小權值的邊，其中u∈U，v∈V-U，則必存在一棵包含邊 (u, v) 的最小生成樹。
（1）普里姆 (Prim) 算法
算法思想：?
????①設 N=(V, E)是連通網，TE是N上最小生成樹中邊的集合。
????②初始令 U={u_0}, (u_0∈V), TE={ }。
????③在所有u∈U，u∈U-V的邊(u,v)∈E中，找一條代價最小的邊(u_0,v_0 )。
????④將(u_0,v_0 )并入集合TE，同時v_0并入U。
????⑤重復上述操作直至U = V為止，則 T=(V,TE)為N的最小生成樹。
?
代碼實現：
void MiniSpanTree_PRIM(MGraph G,VertexType u)//用普里姆算法從第u個頂點出發構造網G的最小生成樹T，輸出T的各條邊。//記錄從頂點集U到V-U的代價最小的邊的輔助數組定義；//closedge[j].lowcost表示在集合U中頂點與第j個頂點對應最小權值
{int k, j, i;k = LocateVex(G,u);for (j = 0; j < G.vexnum; ++j)?? ?//輔助數組的初始化if(j != k){closedge[j].adjvex = u;closedge[j].lowcost = G.arcs[k][j].adj;?? ?
//獲取鄰接矩陣第k行所有元素賦給closedge[j!= k].lowcost}closedge[k].lowcost = 0;?? ??? ?
//初始，U = {u}; ?PrintClosedge(closedge,G.vexnum);for (i = 1; i < G.vexnum; ++i)?? ?\
//選擇其余G.vexnum-1個頂點，因此i從1開始循環{k = minimum(G.vexnum,closedge);?? ??? ?
//求出最小生成樹的下一個結點：第k頂點PrintMiniTree_PRIM(G, closedge, k); ?? ?//輸出生成樹的邊closedge[k].lowcost = 0;?? ??? ??? ??? ?//第k頂點并入U集PrintClosedge(closedge,G.vexnum);for(j = 0;j < G.vexnum; ++j){ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??if(G.arcs[k][j].adj < closedge[j].lowcost)?? ?
//比較第k個頂點和第j個頂點權值是否小于closedge[j].lowcost{closedge[j].adjvex = G.vexs[k];//替換closedge[j]closedge[j].lowcost = G.arcs[k][j].adj;PrintClosedge(closedge,G.vexnum);}}}
}
（2）克魯斯卡爾 (Kruskal) 算法
算法思想：?
????①設連通網 ?N = (V, E )，令最小生成樹初始狀態為只有n個頂點而無邊的非連通圖，T=(V, { })，每個頂點自成一個連通分量。
????②在 E 中選取代價最小的邊，若該邊依附的頂點落在T中不同的連通分量上（即：不能形成環），則將此邊加入到T中；否則，舍去此邊，選取下一條代價最小的邊。
③依此類推，直至 T 中所有頂點都在同一連通分量上為止。
??????
????最小生成樹可能不惟一！
?
拓撲排序
?
（1）有向無環圖
????無環的有向圖，簡稱 DAG (Directed Acycline Graph) 圖。
?
有向無環圖在工程計劃和管理方面的應用：除最簡單的情況之外，幾乎所有的工程都可分為若干個稱作“活動”的子工程，并且這些子工程之間通常受著一定條件的約束，例如：其中某些子工程必須在另一些子工程完成之后才能開始。
對整個工程和系統，人們關心的是兩方面的問題：?
①工程能否順利進行；?
②完成整個工程所必須的最短時間。
對應到有向圖即為進行拓撲排序和求關鍵路徑。?
AOV網：?
????用一個有向圖表示一個工程的各子工程及其相互制約的關系，其中以頂點表示活動，弧表示活動之間的優先制約關系，稱這種有向圖為頂點表示活動的網，簡稱AOV網(Activity On Vertex network)。
例如：排課表
??????
AOV網的特點：
①若從i到j有一條有向路徑，則i是j的前驅；j是i的后繼。
②若< i , j >是網中有向邊，則i是j的直接前驅；j是i的直接后繼。
③AOV網中不允許有回路，因為如果有回路存在，則表明某項活動以自己為先決條件，顯然這是荒謬的。
問題： ???
????問題：如何判別 AOV 網中是否存在回路？
????檢測 AOV 網中是否存在環方法：對有向圖構造其頂點的拓撲有序序列，若網中所有頂點都在它的拓撲有序序列中，則該AOV網必定不存在環。
拓撲排序的方法：
????①在有向圖中選一個沒有前驅的頂點且輸出之。
????②從圖中刪除該頂點和所有以它為尾的弧。
????③重復上述兩步，直至全部頂點均已輸出；或者當圖中不存在無前驅的頂點為止。
????????
????一個AOV網的拓撲序列不是唯一的！
代碼實現：
Status TopologicalSort(ALGraph G)//有向圖G采用鄰接表存儲結構。//若G無回路，則輸出G的頂點的一個拓撲序列并返回OK，否則返回ERROR.//輸出次序按照棧的后進先出原則，刪除頂點，輸出遍歷
{SqStack S;int i, count;int *indegree1 = (int *)malloc(sizeof(int) * G.vexnum);int indegree[12] = {0};FindInDegree(G, indegree);?? ?//求個頂點的入度下標從0開始InitStack(&S);PrintStack(S);for(i = 0; i < G.vexnum; ++i)if(!indegree[i])?? ??? ?//建0入度頂點棧Spush(&S,i);?? ??? ?//入度為0者進棧count = 0;?? ??? ??? ??? ?//對輸出頂點計數while (S.base != S.top){ArcNode* p;pop(&S,&i);VisitFunc(G,i);//第i個輸出棧頂元素對應的頂點，也就是最后進來的頂點?? ?++count;?? ??? ? ?//輸出i號頂點并計數for(p = G.vertices[i].firstarc; p; p = p->nextarc){?? ?//通過循環遍歷第i個頂點的表結點，將表結點中入度都減1int k = p->adjvex;?? ?//對i號頂點的每個鄰接點的入度減1if(!(--indegree[k]))push(&S,k);?? ??? ?//若入度減為0，則入棧}//for}//whileif(count < G.vexnum){printf("\n該有向圖有回路!\n");return ERROR;?? ?//該有向圖有回路}else{printf("\n該有向圖沒有回路!\n");return OK;}
}
關鍵路徑
????把工程計劃表示為有向圖，用頂點表示事件，弧表示活動，弧的權表示活動持續時間。每個事件表示在它之前的活動已經完成，在它之后的活動可以開始。稱這種有向圖為邊表示活動的網，簡稱為 AOE網 (Activity On Edge)。
例如：
設一個工程有11項活動，9個事件。
事件v_1——表示整個工程開始（源點）?
事件v_9——表示整個工程結束（匯點）
?
對AOE網，我們關心兩個問題： ?
①完成整項工程至少需要多少時間？?
②哪些活動是影響工程進度的關鍵？
關鍵路徑——路徑長度最長的路徑。
路徑長度——路徑上各活動持續時間之和。
v_i——表示事件v_i的最早發生時間。假設開始點是v_1，從v_1到〖v�i〗的最長路徑長度。?(?)——表示活動a_i的最早發生時間。
l(?)——表示活動a_i最遲發生時間。在不推遲整個工程完成的前提下，活動a_i最遲必須開始進行的時間。
l(?)-?(?)意味著完成活動a_i的時間余量。
我們把l(?)=?(?)的活動叫做關鍵活動。顯然，關鍵路徑上的所有活動都是關鍵活動，因此提前完成非關鍵活動并不能加快工程進度。
????例如上圖中網，從從v_1到v_9的最長路徑是(v_1,v_2,v_5,v_8,ν_9 )，路徑長度是18，即ν_9的最遲發生時間是18。而活動a_6的最早開始時間是5，最遲開始時間是8，這意味著：如果a_6推遲3天或者延遲3天完成，都不會影響整個工程的完成。因此，分析關鍵路徑的目的是辨別哪些是關鍵活動，以便爭取提高關鍵活動的工效，縮短整個工期。
????由上面介紹可知：辨別關鍵活動是要找l(?)=?(?)的活動。為了求?(?)和l(?)，首先應求得事件的最早發生時間v?(j)和最遲發生時間vl(j)。如果活動a_i由弧?j,k?表示，其持續時間記為dut(?j,k?),則有如下關系：
?(?)= v?(j)
l(?)=vl(k)-dut(?j,k?)
????求v?(j)和vl(j)需分兩步進行：
第一步：從v?(0)=0開始向前遞推
v?(j)=Max{v?(i)+dut(?j,k?)} ???i,j?∈T,j=1,2,…,n-1
其中，T是所有以第j個頂點為頭的弧的集合。
第二步：從vl(n-1)=v?(n-1)起向后遞推
vl(i)=Min{vl(j)-dut(?i,j?)} ??i,j?∈S,i=n-2,…,0
其中，S是所有以第i個頂點為尾的弧的集合。
下面我們以上圖AOE網為例，先求每個事件v_i的最早發生時間，再逆向求每個事件對應的最晚發生時間。再求每個活動的最早發生時間和最晚發生時間，如下面表格：
??????????
在活動的統計表中，活動的最早發生時間和最晚發生時間相等的，就是關鍵活動
關鍵路徑的討論：
①若網中有幾條關鍵路徑，則需加快同時在幾條關鍵路徑上的關鍵活動。 ?????如：a11、a10、a8、a7。?
②如果一個活動處于所有的關鍵路徑上，則提高這個活動的速度，就能縮短整個工程的完成時間。如：a1、a4。
③處于所有關鍵路徑上的活動完成時間不能縮短太多，否則會使原關鍵路徑變成非關鍵路徑。這時必須重新尋找關鍵路徑。如：a1由6天變成3天，就會改變關鍵路徑。
關鍵路徑算法實現：
int CriticalPath(ALGraph G)
{?? ?//因為G是有向網，輸出G的各項關鍵活動SqStack T;int i, j;?? ?ArcNode* p;int k , dut;if(!TopologicalOrder(G,T))return 0;int vl[VexNum];for (i = 0; i < VexNum; i++)vl[i] = ve[VexNum - 1];?? ??? ?//初始化頂點事件的最遲發生時間while (T.base != T.top)?? ??? ??? ?//按拓撲逆序求各頂點的vl值{for(pop(&T, &j), p = G.vertices[j].firstarc; p; p = p->nextarc){k = p->adjvex;?? ?dut = *(p->info);?? ?//dut<j, k>if(vl[k] - dut < vl[j])vl[j] = vl[k] - dut;}//for}//whilefor(j = 0; j < G.vexnum; ++j)?? ?//求ee,el和關鍵活動{for (p = G.vertices[j].firstarc; p; p = p->nextarc){int ee, el;?? ??? ?char tag;k = p->adjvex;?? ?dut = *(p->info);ee = ve[j];?? ?el = vl[k] - dut;tag = (ee == el) ? '*' : ' ';PrintCriticalActivity(G,j,k,dut,ee,el,tag);}}return 1;
}最短路
?
最短路
????典型用途：交通網絡的問題——從甲地到乙地之間是否有公路連通？在有多條通路的情況下，哪一條路最短？
?
????交通網絡用有向網來表示：頂點——表示城市，弧——表示兩個城市有路連通，弧上的權值——表示兩城市之間的距離、交通費或途中所花費的時間等。
????如何能夠使一個城市到另一個城市的運輸時間最短或運費最省？這就是一個求兩座城市間的最短路徑問題。
????問題抽象：在有向網中A點（源點）到達B點（終點）的多條路徑中，尋找一條各邊權值之和最小的路徑，即最短路徑。最短路徑與最小生成樹不同，路徑上不一定包含n個頂點，也不一定包含n - 1條邊。
???常見最短路徑問題：單源點最短路徑、所有頂點間的最短路徑
（1）如何求得單源點最短路徑？
????窮舉法：將源點到終點的所有路徑都列出來，然后在其中選最短的一條。但是，當路徑特別多時，特別麻煩；沒有規律可循。
????迪杰斯特拉（Dijkstra）算法：按路徑長度遞增次序產生各頂點的最短路徑。
路徑長度最短的最短路徑的特點：
????在此路徑上，必定只含一條弧 <v_0, v_1>，且其權值最小。由此，只要在所有從源點出發的弧中查找權值最小者。
下一條路徑長度次短的最短路徑的特點：
①、直接從源點到v_2<v_0, v_2>（只含一條弧）；
②、從源點經過頂點v_1，再到達v_2<v_0, v_1>,<v_1, v_2>（由兩條弧組成）
再下一條路徑長度次短的最短路徑的特點：
????有以下四種情況：
????①、直接從源點到v_3<v_0, v_3>（由一條弧組成）；
????②、從源點經過頂點v_1，再到達v_3<v_0, v_1>,<v_1, v_3>（由兩條弧組成）；
????③、從源點經過頂點v_2，再到達v_3<v_0, v_2>,<v_2, v_3>（由兩條弧組成）；
????④、從源點經過頂點v_1 ?,v_2，再到達v_3<v_0, v_1>,<v_1, v_2>,<v_2, v_3>（由三條弧組成）；
其余最短路徑的特點:????
????①、直接從源點到v_i<v_0, v_i>（只含一條弧）；
????②、從源點經過已求得的最短路徑上的頂點，再到達v_i（含有多條弧）。
Dijkstra算法步驟：
????初始時令S={v_0}, ?T={其余頂點}。T中頂點對應的距離值用輔助數組D存放。
????D[i]初值：若<v_0, v_i>存在，則為其權值；否則為∞。?
????從T中選取一個其距離值最小的頂點v_j，加入S。對T中頂點的距離值進行修改：若加進v_j作中間頂點，從v_0到v_i的距離值比不加 vj 的路徑要短，則修改此距離值。
????重復上述步驟，直到 S = V 為止。
算法實現：
void ShortestPath_DIJ(MGraph G,int v0,PathMatrix &P,ShortPathTable &D)
{ // 用Dijkstra算法求有向網 G 的 v0 頂點到其余頂點v的最短路徑P[v]及帶權長度D[v]。// 若P[v][w]為TRUE,則 w 是從 v0 到 v 當前求得最短路徑上的頂點。 ?P是存放最短路徑的矩陣，經過頂點變成TRUE// final[v]為TRUE當且僅當 v∈S,即已經求得從v0到v的最短路徑。int v,w,i,j,min;Status final[MAX_VERTEX_NUM];for(v = 0 ;v < G.vexnum ;++v){final[v] = FALSE;D[v] = G.arcs[v0][v].adj;?? ??? ?//將頂點數組中下標對應是 v0 和 v的距離給了D[v]for(w = 0;w < G.vexnum; ++w)P[v][w] = FALSE;?? ??? ??? ?//設空路徑if(D[v] < INFINITY){P[v][v0] = TRUE;P[v][v] = TRUE;}}D[v0]=0;final[v0]= TRUE; /* 初始化,v0頂點屬于S集 */for(i = 1;i < G.vexnum; ++i) /* 其余G.vexnum-1個頂點 */{ /* 開始主循環,每次求得v0到某個v頂點的最短路徑,并加v到S集 */min = INFINITY; /* 當前所知離v0頂點的最近距離 */for(w = 0;w < G.vexnum; ++w)if(!final[w]) /* w頂點在V-S中 */if(D[w] < min){v = w;min = D[w];} /* w頂點離v0頂點更近 */final[v] = TRUE; /* 離v0頂點最近的v加入S集 */for(w = 0;w < G.vexnum; ++w) /* 更新當前最短路徑及距離 */{if(!final[w] && min < INFINITY && G.arcs[v][w].adj < INFINITY && (min + G.arcs[v][w].adj < D[w])){ /* 修改D[w]和P[w],w∈V-S */D[w] = min + G.arcs[v][w].adj;for(j = 0;j < G.vexnum;++j)P[w][j] = P[v][j];P[w][w] = TRUE;}}}
}簡單迷宮問題
迷宮實驗是取自心理學的一個古典實驗。在該實驗中，把一只老鼠從一個無頂大盒子的門放入，在盒子中設置了許多墻，對行進方向形成了多處阻擋。盒子僅有一個出口，在出口處放置一塊奶酪，吸引老鼠在迷宮中尋找道路以到達出口。對同一只老鼠重復進行上述實驗，一直到老鼠從入口到出口，而不走錯一步。老鼠經過多次試驗終于得到它學習走通迷宮的路線。設計一個計算機程序對任意設定的迷宮，求出一條從入口到出口的通路，或得出沒有通路的結論。
數組元素值為1表示該位置是墻壁，不能通行；元素值為0表示該位置是通路。假定從mg[1][1]出發，出口位于mg[n][m]
用一種標志在二維數組中標出該條通路，并在屏幕上輸出二維數組。
m=[[1,1,1,0,1,1,1,1,1,1],[1,0,0,0,0,0,0,0,1,1],[1,0,1,1,1,1,1,0,0,1],[1,0,1,0,0,0,0,1,0,1],[1,0,1,0,1,1,0,0,0,1],[1,0,0,1,1,0,1,0,1,1],[1,1,1,1,0,0,0,0,1,1],[1,0,0,0,0,1,1,1,0,0],[1,0,1,1,0,0,0,0,0,1],[1,1,1,1,1,1,1,1,1,1]]
sta1=0;sta2=3;fsh1=7;fsh2=9;success=0
def LabyrinthRat():print('顯示迷宮：')for i in range(len(m)):print(m[i])print('入口：m[%d][%d]：出口：m[%d][%d]'%(sta1,sta2,fsh1,fsh2))if (visit(sta1,sta2))==0: print('沒有找到出口')else:print('顯示路徑：')for i in range(10):print(m[i])
def visit(i,j):m[i][j]=2global successif(i==fsh1)and(j==fsh2): success=1if(success!=1)and(m[i-1][j]==0): visit(i-1,j)if(success!=1)and(m[i+1][j]==0): visit(i+1,j)if(success!=1)and(m[i][j-1]==0): visit(i,j-1)if(success!=1)and(m[i][j+1]==0): visit(i,j+1)if success!=1: m[i][j]=3return success
LabyrinthRat()深搜DFS\廣搜BFS?
首先，不管是BFS還是DFS，由于時間和空間的局限性，它們只能解決數據量比較小的問題。
深搜，顧名思義，它從某個狀態開始，不斷的轉移狀態，直到無法轉移，然后退回到上一步的狀態，繼續轉移到其他狀態，不斷重復，直到找到最終的解。從實現上來說，棧結構是后進先出，可以很好的保存上一步狀態并利用。所以根據深搜和棧結構的特點，深度優先搜索利用遞歸函數（棧）來實現，只不過這個棧是系統幫忙做的，不太明顯罷了。
?
廣搜和深搜的搜索順序不同，它是先搜索離初始狀態比較近的狀態，搜索順序是這樣的：初始狀態---------->一步能到的狀態--------->兩步能到的狀態......從實現上說，它是通過隊列實現的，并且是我們自己做隊列。一般解決最短路問題，因為第一個搜到的一定是最短路。
下面通過兩道簡單例題簡單的入個門。
深搜例題
poj2386
http://poj.org/problem?id=2386
題目大意：上下左右斜著挨著都算一個池子，看圖中有幾個池子。
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.例如本圖就是有三個池子采用深度優先搜索，從任意的w開始，不斷把鄰接的部分用'.'代替，1次DFS后與初始這個w連接的所有w就全都被替換成'.'，因此直到圖中不再存在W為止。
核心代碼：
char field[maxn][maxn];//圖
int n,m;長寬
void dfs(int x,int y)
{field[x][y]='.';//先做了標記//循環遍歷八個方向for(int dx=-1;dx<=1;dx++){for(int dy=-1;dy<=1;dy++){int nx=x+dx,ny=y+dy;//判斷(nx,ny)是否在園子里，以及是否有積水if(0<=nx&&nx<n&&0<=ny&&ny<m&&field[nx][ny]=='W'){dfs(nx,ny);}}}
}
void solve()
{int res=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(field[i][j]=='W'){//從有積水的地方開始搜dfs(i,j);res++;//搜幾次就有幾個池子}}}printf("%d\n",res);
}廣搜例題：
迷宮的最短路徑
給定一個大小為N×M的迷宮。迷宮由通道和墻壁組成，每一步可以向鄰接的上下左右四個的通道移動。請求出從起點到終點所需的最小步數。請注意，本題假定從起點一定可以移動到終點。（N,M≤100）（'#', '.' , 'S', 'G'分別表示墻壁、通道、起點和終點）
輸入：
10 10
#S######.#
......#..#
.#.##.##.#
.#........
##.##.####
....#....#
.#######.#
....#.....
.####.###.
....#...G#
輸出：
22
小白書上部分代碼：
typedef pair<int, int> P;
char maze[maxn][maxn];
int n, m, sx, sy, gx, gy,d[maxn][maxn];//到各個位置的最短距離的數組
int dx[4] = { 1,0,-1,0 }, dy[4]= { 0,1,0,-1 };//4個方向移動的向量
int bfs()//求從(sx,sy)到(gx,gy)的最短距離，若無法到達則是INF
{queue<P> que; for (int i = 0; i < n; i++)for (int j = 0; j < m; j++)d[i][j] = INF;//所有的位置都初始化為INFque.push(P(sx, sy));//將起點加入隊列中d[sx][sy] = 0;//并把起點的距離設置為0while (que.size())//不斷循環直到隊列的長度為0{P p = que.front();// 從隊列的最前段取出元素que.pop();//刪除該元素if (p.first == gx&&p.second == gy)//是終點結束break;for (int i = 0; i < 4; i++)//四個方向的循環{int nx = p.first + dx[i],ny = p.second + dy[i];//移動后的位置標記為(nx,ny)if (0 <= nx&&nx < n && 0 <= ny&&ny < m&&maze[nx][ny] != '#'&&d[nx][ny] == INF)//判斷是否可以移動以及是否訪問過(即d[nx][ny]!=INF）{que.push(P(nx, ny));//可以移動，添加到隊列d[nx][ny] = d[p.first][p.second] + 1;//到該位置的距離為到p的距離+1}}}return d[gx][gy];
}經典了兩個題結束了，好題鏈接持續更新。。。。。。
?皇后問題
?
八皇后問題是一個以國際象棋為背景的問題：如何能夠在 8×8 的國際象棋棋盤上放置八個皇后，使得任何一個皇后都無法直接吃掉其他的皇后？為了達到此目的，任兩個皇后都不能處于同一條橫行、縱行或斜線上。八皇后問題可以推廣為更一般的n皇后擺放問題：這時棋盤的大小變為n1×n1，而皇后個數也變成n2。而且僅當 n2 ≥ 1 或 n1 ≥ 4 時問題有解。
皇后問題是非常著名的問題，作為一個棋盤類問題，毫無疑問，用暴力搜索的方法來做是一定可以得到正確答案的，但在有限的運行時間內，我們很難寫出速度可以忍受的搜索，部分棋盤問題的最優解不是搜索，而是動態規劃，某些棋盤問題也很適合作為狀態壓縮思想的解釋例題。
進一步說，皇后問題可以用人工智能相關算法和遺傳算法求解，可以用多線程技術縮短運行時間。本文不做討論。
（本文不展開講狀態壓縮，以后再說）
?
一般思路：
?
N*N的二維數組，在每一個位置進行嘗試，在當前位置上判斷是否滿足放置皇后的條件（這一點的行、列、對角線上，沒有皇后）。
?
優化1：
?
既然知道多個皇后不能在同一行，我們何必要在同一行的不同位置放多個來嘗試呢？
我們生成一維數組record，record[i]表示第i行的皇后放在了第幾列。對于每一行，確定當前record值即可，因為每行只能且必須放一個皇后，放了一個就無需繼續嘗試。那么對于當前的record[i]，查看record[0...i-1]的值，是否有j = record[k]（同列）、|record[k] - j| = | k-i |（同一斜線）的情況。由于我們的策略，無需檢查行（每行只放一個）。
public class NQueens {public static int num1(int n) {if (n < 1) {return 0;}int[] record = new int[n];return process1(0, record, n);}public static int process1(int i, int[] record, int n) {if (i == n) {return 1;}int res = 0;for (int j = 0; j < n; j++) {if (isValid(record, i, j)) {record[i] = j;res += process1(i + 1, record, n);}}//對于當前行，依次嘗試每列return res;}
//判斷當前位置是否可以放置public static boolean isValid(int[] record, int i, int j) {for (int k = 0; k < i; k++) {if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {return false;}}return true;}public static void main(String[] args) {int n = 8;System.out.println(num1(n));}
}
優化2：
?
分析：棋子對后續過程的影響范圍：本行、本列、左右斜線。
黑色棋子影響區域為紅色
本行影響不提，根據優化一已經避免
本列影響，一直影響D列，直到第一行在D放棋子的所有情況結束。
?
左斜線：每向下一行，實際上對當前行的影響區域就向左移動
比如：
嘗試第二行時，黑色棋子影響的是我們的第三列；
嘗試第三行時，黑色棋子影響的是我們的第二列；
嘗試第四行時，黑色棋子影響的是我們的第一列；
嘗試第五行及以后幾行，黑色棋子對我們并無影響。
?
右斜線則相反：
隨著行序號增加，影響的列序號也增加，直到影響的列序號大于8就不再影響。
?
我們對于之前棋子影響的區域，可以用二進制數字來表示，比如:
每一位，用01代表是否影響。
比如上圖，對于第一行，就是00010000
嘗試第二行時，數字變為00100000
第三行：01000000
第四行：10000000
?
對于右斜線的數字，同理：
第一行00010000，之后向右移：00001000，00000100，00000010，00000001，直到全0不影響。
?
同理，我們對于多行數據，也同樣可以記錄了
比如在第一行我們放在了第四列：
第二行放在了G列，這時左斜線記錄為00100000（第一個棋子的影響）+00000010（當前棋子的影響）=00100010。
到第三行數字繼續左移：01000100，然后繼續加上我們的選擇，如此反復。
?
這樣，我們對于當前位置的判斷，其實可以通過左斜線變量、右斜線變量、列變量，按位或運算求出（每一位中，三個數有一個是1就不能再放）。
具體看代碼：
注：怎么排版就炸了呢。。。貼一張圖吧
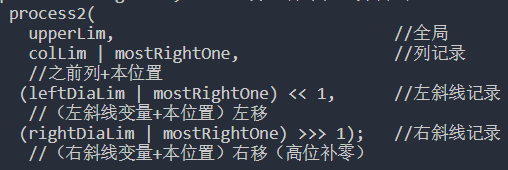
public class NQueens {public static int num2(int n) {// 因為本方法中位運算的載體是int型變量，所以該方法只能算1~32皇后問題// 如果想計算更多的皇后問題，需使用包含更多位的變量if (n < 1 || n > 32) {return 0;}int upperLim = n == 32 ? -1 : (1 << n) - 1;//upperLim的作用為棋盤大小，比如8皇后為00000000 00000000 00000000 11111111//32皇后為11111111 11111111 11111111 11111111return process2(upperLim, 0, 0, 0);}public static int process2(int upperLim, int colLim, int leftDiaLim,int rightDiaLim) {if (colLim == upperLim) {return 1;}int pos = 0; //pos：所有的合法位置int mostRightOne = 0; //所有合法位置的最右位置//所有記錄按位或之后取反，并與全1按位與，得出所有合法位置pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));int res = 0;//計數while (pos != 0) {mostRightOne = pos & (~pos + 1);//取最右的合法位置pos = pos - mostRightOne; //去掉本位置并嘗試res += process2(upperLim, //全局colLim | mostRightOne, //列記錄//之前列+本位置(leftDiaLim | mostRightOne) << 1, //左斜線記錄//（左斜線變量+本位置）左移 (rightDiaLim | mostRightOne) >>> 1); //右斜線記錄//（右斜線變量+本位置）右移（高位補零）}return res;}public static void main(String[] args) {int n = 8;System.out.println(num2(n));}
}
完整測試代碼：
32皇后：結果/時間
暴力搜：時間就太長了，懶得測。。。
public class NQueens {public static int num1(int n) {if (n < 1) {return 0;}int[] record = new int[n];return process1(0, record, n);}public static int process1(int i, int[] record, int n) {if (i == n) {return 1;}int res = 0;for (int j = 0; j < n; j++) {if (isValid(record, i, j)) {record[i] = j;res += process1(i + 1, record, n);}}return res;}public static boolean isValid(int[] record, int i, int j) {for (int k = 0; k < i; k++) {if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {return false;}}return true;}public static int num2(int n) {if (n < 1 || n > 32) {return 0;}int upperLim = n == 32 ? -1 : (1 << n) - 1;return process2(upperLim, 0, 0, 0);}public static int process2(int upperLim, int colLim, int leftDiaLim,int rightDiaLim) {if (colLim == upperLim) {return 1;}int pos = 0;int mostRightOne = 0;pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));int res = 0;while (pos != 0) {mostRightOne = pos & (~pos + 1);pos = pos - mostRightOne;res += process2(upperLim, colLim | mostRightOne,(leftDiaLim | mostRightOne) << 1,(rightDiaLim | mostRightOne) >>> 1);}return res;}public static void main(String[] args) {int n = 32;long start = System.currentTimeMillis();System.out.println(num2(n));long end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + "ms");start = System.currentTimeMillis();System.out.println(num1(n));end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + "ms");}
}
二叉搜索樹實現
本文給出二叉搜索樹介紹和實現
?
首先說它的性質：所有的節點都滿足，左子樹上所有的節點都比自己小，右邊的都比自己大。
?
那這個結構有什么有用呢？
首先可以快速二分查找。還可以中序遍歷得到升序序列，等等。。。
基本操作：
1、插入某個數值
2、查詢是否包含某個數值
3、刪除某個數值
?
根據實現不同，還可以實現其他很多種操作。
?
實現思路思路：
前兩個操作很好想，就是不斷比較，大了往左走，小了往右走。到空了插入，或者到空都沒找到。
而刪除稍微復雜一些，有下面這幾種情況：
1、需要刪除的節點沒有左兒子，那就把右兒子提上去就好了。
2、需要刪除的節點有左兒子，這個左兒子沒有右兒子，那么就把左兒子提上去
3、以上都不滿足，就把左兒子子孫中最大節點提上來。
?
當然，反過來也是成立的，比如右兒子子孫中最小的節點。
?
下面來敘述為什么可以這么做。
下圖中A為待刪除節點。
第一種情況：
?
1、去掉A，把c提上來，c也是小于x的沒問題。
2、根據定義可知，x左邊的所有點都小于它，把c提上來不影響規則。
?
第二種情況
?
3、B<A<C,所以B<C,根據剛才的敘述，B可以提上去，c可以放在b右邊，不影響規則
4、同理
?
第三種情況
?
5、注意：是把黑色的提升上來，不是所謂的最右邊的那個，因為當初向左拐了，他一定小。
因為黑色是最大，比B以及B所有的孩子都大，所以讓B當左孩子沒問題
而黑點小于A，也就小于c，所以可以讓c當右孩子
大概證明就這樣。。
下面我們用代碼實現并通過注釋理解
上次鏈表之類的用的c，循環來寫的。這次就c++函數遞歸吧，不同方式練習。
定義
struct node
{int val;//數據node *lch,*rch;//左右孩子
};插入
node *insert(node *p,int x){if(p==NULL)//直到空就創建節點{node *q=new node;q->val=x;q->lch=q->rch=NULL;return p;}if(x<p->val)p->lch=insert(p->lch,x);else p->lch=insert(p->rch,x);return p;//依次返回自己，讓上一個函數執行。}查找
bool find(node *p,int x){if(p==NULL)return false;else if(x==p->val)return true;else if(x<p->val)return find(p->lch,x);else return find(p->rch,x);}刪除
node *remove(node *p,int x){if(p==NULL)return NULL;else if(x<p->val)p->lch=remove(p->lch,x);else if(x>p->val)p->lch=remove(p->rch,x);//以下為找到了之后else if(p->lch==NULL)//情況1{node *q=p->rch;delete p;return q;}else if(p->lch->rch)//情況2{node *q=p->lch;q->rch=p->rch;delete p;return q;}else{node *q;for(q=p->lch;q->rch->rch!=NULL;q=q->rch);//找到最大節點的前一個node *r=q->rch;//最大節點q->rch=r->lch;//最大節點左孩子提到最大節點位置r->lch=p->lch;//調整黑點左孩子為Br->rch=p->rch;//調整黑點右孩子為cdelete p;//刪除return r;//返回給父}return p;}Abstract Self-Balancing Binary Search Tree
?
二叉搜索樹
?
二叉查找樹（Binary Search Tree），（又：二叉搜索樹，二叉排序樹）它或者是一棵空樹，或者是具有下列性質的二叉樹： 若它的左子樹不空，則左子樹上所有結點的值均小于它的根結點的值； 若它的右子樹不空，則右子樹上所有結點的值均大于它的根結點的值； 它的左、右子樹也分別為二叉排序樹。
具體介紹和實現：https://blog.csdn.net/hebtu666/article/details/81741034
我們知道，對于一般的二叉搜索樹（Binary Search Tree），其期望高度（即為一棵平衡樹時）為log2n，其各操作的時間復雜度（O(log2n)）同時也由此而決定。但是，在某些極端的情況下（如在插入的序列是有序的時），二叉搜索樹將退化成近似鏈或鏈，
此時，其操作的時間復雜度將退化成線性的，即O(n)。我們可以通過隨機化建立二叉搜索樹來盡量的避免這種情況，但是在進行了多次的操作之后，由于在刪除時，我們總是選擇將待刪除節點的后繼代替它本身，這樣就會造成總是右邊的節點數目減少，以至于樹向左偏沉。這同時也會造成樹的平衡性受到破壞，提高它的操作的時間復雜度。
?
概念引入
?
Abstract Self-Balancing Binary Search Tree：自平衡二叉搜索樹
顧名思義：它在面對任意節點插入和刪除時自動保持其高度
常用算法有紅黑樹、AVL、Treap、伸展樹、SB樹等。在平衡二叉搜索樹中，我們可以看到，其高度一般都良好地維持在O（log（n）），大大降低了操作的時間復雜度。這些結構為可變有序列表提供了有效的實現，并且可以用于其他抽象數據結構，例如關聯數組，優先級隊列和集合。
對于這些結構，他們都有自己的平衡性，比如：
AVL樹
具有以下性質：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，并且左右兩個子樹都是一棵平衡二叉樹。
根據定義可知，這是根據深度最嚴苛的標準了，左右子樹高度不能差的超過1.
具體介紹和實現：https://blog.csdn.net/hebtu666/article/details/85047648
?
紅黑樹
特性:
（1）每個節點或者是黑色，或者是紅色。
（2）根節點是黑色。
（3）每個葉子節點（NIL）是黑色。?[注意：這里葉子節點，是指為空(NIL或NULL)的葉子節點！]
（4）如果一個節點是紅色的，則它的子節點必須是黑色的。
（5）從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。
根據定義，確保沒有一條路徑會比其他路徑長出2倍。
?
size balance tree
Size Balanced Tree（簡稱SBT）是一自平衡二叉查找樹，是在計算機科學中用到的一種數據結構。它是由中國廣東中山紀念中學的陳啟峰發明的。陳啟峰于2006年底完成論文《Size Balanced Tree》，并在2007年的全國青少年信息學奧林匹克競賽冬令營中發表。由于SBT的拼寫很容易找到中文諧音，它常被中國的信息學競賽選手和ACM/ICPC選手們戲稱為“傻B樹”、“Super BT”等。相比紅黑樹、AVL樹等自平衡二叉查找樹，SBT更易于實現。據陳啟峰在論文中稱，SBT是“目前為止速度最快的高級二叉搜索樹”。SBT能在O(log n)的時間內完成所有二叉搜索樹（BST）的相關操作，而與普通二叉搜索樹相比，SBT僅僅加入了簡潔的核心操作Maintain。由于SBT賴以保持平衡的是size域而不是其他“無用”的域，它可以很方便地實現動態順序統計中的select和rank操作。
對于SBT的每一個結點 t,有如下性質：
???性質(a) s[ right[t] ]≥s[ left [ left[ t ] ] ], s[ right [ left[t] ] ]
???性質(b) s[ left[t] ]≥s[right[ right[t] ] ], s[ left[ right[t] ] ]
即.每棵子樹的大小不小于其兄弟的子樹大小。
?
伸展樹
伸展樹（Splay Tree）是一種二叉排序樹，它能在O(log n)內完成插入、查找和刪除操作。它由Daniel Sleator和Robert Tarjan創造。它的優勢在于不需要記錄用于平衡樹的冗余信息。在伸展樹上的一般操作都基于伸展操作。
?
Treap
Treap是一棵二叉排序樹，它的左子樹和右子樹分別是一個Treap，和一般的二叉排序樹不同的是，Treap紀錄一個額外的數據，就是優先級。Treap在以關鍵碼構成二叉排序樹的同時，還滿足堆的性質(在這里我們假設節點的優先級大于該節點的孩子的優先級)。但是這里要注意的是Treap和二叉堆有一點不同，就是二叉堆必須是完全二叉樹，而Treap并不一定是。
?
?
?
?
對比可以發現，AVL樹對平衡性的要求比較嚴苛，每插入一個節點就很大概率面臨調整。
而紅黑樹對平衡性的要求沒有那么嚴苛。可能是多次插入攢夠了一下調整。。。
?
把每一個樹的細節都扣清楚是一件挺無聊的事。。雖然據說紅黑樹都成了面試必問內容，但是實在是不想深究那些細節，這些樹的基本操作也無非是那么兩種：左旋，右旋。這些樹的所有操作和情況，都是這兩種動作的組合罷了。
所以本文先介紹這兩種基本操作，等以后有時間（可能到找工作時），再把紅黑樹等結構的細節補上。
?
最簡單的旋轉
?
最簡單的例子：
這棵樹，左子樹深度為2，右子樹深度為0，所以，根據AVL樹或者紅黑樹的標準，它都不平衡。。
那怎么辦？轉過來：
是不是就平衡了？
這就是我們的順時針旋轉，又叫，右旋，因為是以2為軸，把1轉下來了。
左旋同理。
?
帶子樹旋轉
問題是，真正轉起來可沒有這么簡單：
這才是一顆搜索樹的樣子啊
ABCD都代表是一顆子樹。我們這三個點轉了可不能不管這些子樹啊對不對。
好，我們想想這些子樹怎么辦。
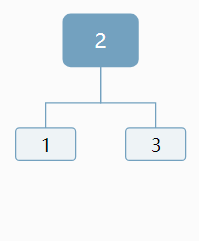
首先，AB子樹沒有關系，放在原地即可。
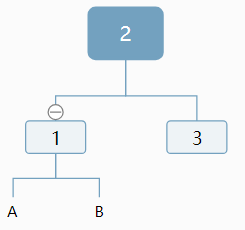
D作為3的右子樹，也可以不動，那剩下一個位置，會不會就是放C子樹呢？
我們想想能否這樣做。
原來：
1）C作為2的右子樹，內任何元素都比2大。
2）C作為3左子樹的一部分，內任何元素都比3小。
轉之后：
1）C作為2的右子樹的一部分，內任何元素都比2大。
2）C作為3左子樹，內任何元素都比3小。
所以，C子樹可以作為3的左子樹，沒有問題。
這樣，我們的操作就介紹完了。
這種基本的變換達到了看似把樹變的平衡的效果。
左右旋轉類似
?
代碼實現
對于Abstract BinarySearchTree類，上面網址已經給出了思路和c++代碼實現，把java再貼出來也挺無趣的，所以希望大家能自己實現。
抽象自平衡二叉搜索樹（AbstractSelfBalancingBinarySearchTree）的所有操作都是建立在二叉搜索樹（BinarySearchTree?）操作的基礎上來進行的。
各種自平衡二叉搜索樹（AVL、紅黑樹等）的操作也是由Abstract自平衡二叉搜索樹的基本操作：左旋、右旋構成。這個文章只寫了左旋右旋基本操作，供以后各種selfBalancingBinarySearchTree使用。
public abstract class AbstractSelfBalancingBinarySearchTree extends AbstractBinarySearchTree {protected Node rotateRight(Node node) {Node temp = node.left;//節點2temp.parent = node.parent;//節點3的父(旋轉后節點2的父)node.left = temp.right;//節點3接收節點2的右子樹if (node.left != null) {node.left.parent = node;}temp.right = node;//節點3變為節點2的右孩子node.parent = temp;//原來節點3的父（若存在），孩子變為節點2if (temp.parent != null) {if (node == temp.parent.left) {temp.parent.left = temp;} else {temp.parent.right = temp;}} else {root = temp;}return temp;}protected Node rotateLeft(Node node) {Node temp = node.right;temp.parent = node.parent;node.right = temp.left;if (node.right != null) {node.right.parent = node;}temp.left = node;node.parent = temp;if (temp.parent != null) {if (node == temp.parent.left) {temp.parent.left = temp;} else {temp.parent.right = temp;}} else {root = temp;}return temp;}
}?
AVL Tree
?
前言
?
希望讀者
了解二叉搜索樹
了解左旋右旋基本操作
https://blog.csdn.net/hebtu666/article/details/84992363
直觀感受直接到文章底部，有正確的調整策略動畫，自行操作。
二叉搜索樹
?
二叉查找樹（Binary Search Tree），（又：二叉搜索樹，二叉排序樹）它或者是一棵空樹，或者是具有下列性質的二叉樹： 若它的左子樹不空，則左子樹上所有結點的值均小于它的根結點的值； 若它的右子樹不空，則右子樹上所有結點的值均大于它的根結點的值； 它的左、右子樹也分別為二叉排序樹。
具體介紹和實現：https://blog.csdn.net/hebtu666/article/details/81741034
我們知道，對于一般的二叉搜索樹（Binary Search Tree），其期望高度（即為一棵平衡樹時）為log2n，其各操作的時間復雜度（O(log2n)）同時也由此而決定。但是，在某些極端的情況下（如在插入的序列是有序的時），二叉搜索樹將退化成近似鏈或鏈，
此時，其操作的時間復雜度將退化成線性的，即O(n)。我們可以通過隨機化建立二叉搜索樹來盡量的避免這種情況，但是在進行了多次的操作之后，由于在刪除時，我們總是選擇將待刪除節點的后繼代替它本身，這樣就會造成總是右邊的節點數目減少，以至于樹向左偏沉。這同時也會造成樹的平衡性受到破壞，提高它的操作的時間復雜度。
?
AVL Tree
在計算機科學中，AVL樹是最先發明的自平衡二叉查找樹。在AVL樹中任何節點的兩個子樹的高度最大差別為1，所以它也被稱為高度平衡樹。增加和刪除可能需要通過一次或多次樹旋轉來重新平衡這個樹。AVL樹得名于它的發明者G. M. Adelson-Velsky和E. M. Landis，他們在1962年的論文《An algorithm for the organization of information》中發表了它。
這種結構是對平衡性要求最嚴苛的self-Balancing Binary Search Tree。
旋轉操作繼承自self-Balancing Binary Search Tree
public class AVLTree extends AbstractSelfBalancingBinarySearchTree旋轉
上面網址中已經介紹了二叉搜索樹的調整和自平衡二叉搜索樹的基本操作（左旋右旋），上篇文章我是這樣定義左旋的：
達到了? ?看似? ?更平衡的效果。
我們回憶一下：
看起來好像不是很平，對嗎？我們轉一下：
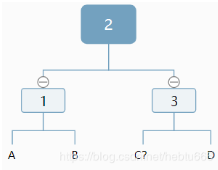
看起來平了很多。
但！是！
只是看起來而已。
我們知道。ABCD其實都是子樹，他們也有自己的深度，如果是這種情況：
我們簡化一下：
轉之后(A上來，3作為A的右孩子，A的右子樹作為新的3的左孩子）：
沒錯，旋轉確實讓樹變平衡了，這是因為，不平衡是由A的左子樹造成的，A的左子樹深度更深。
我們這樣旋轉實際上是讓
A的左子樹相對于B提上去了兩層，深度相對于B，-2，
A的右子樹相對于B提上去了一層，深度相對于B，-1.
而如果是這樣的：
旋轉以后：
依舊是不平的。
那我們怎么解決這個問題呢？
先3的左子樹旋轉：
細節問題：不再講解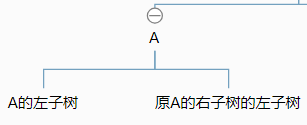
這樣，我們的最深處又成了左子樹的左子樹。然后再按原來旋轉就好了。
?
旋轉總結
?
那我們來總結一下旋轉策略：
單向右旋平衡處理LL：
由于在*a的左子樹根結點的左子樹上插入結點，*a的平衡因子由1增至2，致使以*a為根的子樹失去平衡，則需進行一次右旋轉操作；
單向左旋平衡處理RR：
由于在*a的右子樹根結點的右子樹上插入結點，*a的平衡因子由-1變為-2，致使以*a為根的子樹失去平衡，則需進行一次左旋轉操作；
雙向旋轉（先左后右）平衡處理LR：
由于在*a的左子樹根結點的右子樹上插入結點，*a的平衡因子由1增至2，致使以*a為根的子樹失去平衡，則需進行兩次旋轉（先左旋后右旋）操作。
雙向旋轉（先右后左）平衡處理RL：
由于在*a的右子樹根結點的左子樹上插入結點，*a的平衡因子由-1變為-2，致使以*a為根的子樹失去平衡，則需進行兩次旋轉（先右旋后左旋）操作。
?
深度的記錄
?
我們解決了調整問題，但是我們怎么發現樹不平衡呢？總不能沒插入刪除一次都遍歷一下求深度吧。
當然要記錄一下了。
我們需要知道左子樹深度和右子樹深度。這樣，我們可以添加兩個變量，記錄左右子樹的深度。
但其實不需要，只要記錄自己的深度即可。然后左右子樹深度就去左右孩子去尋找即可。
這樣就引出了一個問題：深度的修改、更新策略是什么呢？
單個節點的深度更新
本棵樹的深度=（左子樹深度，右子樹深度）+1
所以寫出節點node的深度更新方法：
private static final void updateHeight(AVLNode node) {
//不存在孩子，為-1，最后+1，深度為0int leftHeight = (node.left == null) ? -1 : ((AVLNode) node.left).height;int rightHeight = (node.right == null) ? -1 : ((AVLNode) node.right).height;node.height = 1 + Math.max(leftHeight, rightHeight);}?
寫出旋轉代碼
配合上面的方法和文章頭部給出文章Abstract Self-Balancing Binary Search Tree的旋轉，我們可以AVL樹的四種旋轉：
private Node avlRotateLeft(Node node) {Node temp = super.rotateLeft(node);updateHeight((AVLNode)temp.left);updateHeight((AVLNode)temp);return temp;}private Node avlRotateRight(Node node) {Node temp = super.rotateRight(node);updateHeight((AVLNode)temp.right);updateHeight((AVLNode)temp);return temp;}protected Node doubleRotateRightLeft(Node node) {node.right = avlRotateRight(node.right);return avlRotateLeft(node);}protected Node doubleRotateLeftRight(Node node) {node.left = avlRotateLeft(node.left);return avlRotateRight(node);}請自行模擬哪些節點的深度記錄需要修改。
?
總寫調整方法
?
我們寫出了旋轉的操作和相應的深度更新。
現在我們把這些方法分情況總寫。
private void rebalance(AVLNode node) {while (node != null) {Node parent = node.parent;int leftHeight = (node.left == null) ? -1 : ((AVLNode) node.left).height;int rightHeight = (node.right == null) ? -1 : ((AVLNode) node.right).height;int nodeBalance = rightHeight - leftHeight;if (nodeBalance == 2) {if (((AVLNode)node.right.right).height+1 == rightHeight) {node = (AVLNode)avlRotateLeft(node);break;} else {node = (AVLNode)doubleRotateRightLeft(node);break;}} else if (nodeBalance == -2) {if (((AVLNode)node.left.left).height+1 == leftHeight) {node = (AVLNode)avlRotateRight(node);break;} else {node = (AVLNode)doubleRotateLeftRight(node);break;}} else {updateHeight(node);//平衡就一直往上更新高度}node = (AVLNode)parent;}}插入完工
?
我們的插入就完工了。
public Node insert(int element) {Node newNode = super.insert(element);//插入rebalance((AVLNode)newNode);//調整return newNode;}?
刪除
也是一樣的思路，自底向上，先一路修改高度后，進行rebalance調整。
public Node delete(int element) {Node deleteNode = super.search(element);if (deleteNode != null) {Node successorNode = super.delete(deleteNode);//結合上面網址二叉搜索樹實現的情況介紹if (successorNode != null) {// if replaced from getMinimum(deleteNode.right) // then come back there and update heightsAVLNode minimum = successorNode.right != null ? (AVLNode)getMinimum(successorNode.right) : (AVLNode)successorNode;recomputeHeight(minimum);rebalance((AVLNode)minimum);} else {recomputeHeight((AVLNode)deleteNode.parent);//先修改rebalance((AVLNode)deleteNode.parent);//再調整}return successorNode;}return null;}/*** Recomputes height information from the node and up for all of parents. It needs to be done after delete.*/private void recomputeHeight(AVLNode node) {while (node != null) {node.height = maxHeight((AVLNode)node.left, (AVLNode)node.right) + 1;node = (AVLNode)node.parent;}}/*** Returns higher height of 2 nodes. */private int maxHeight(AVLNode node1, AVLNode node2) {if (node1 != null && node2 != null) {return node1.height > node2.height ? node1.height : node2.height;} else if (node1 == null) {return node2 != null ? node2.height : -1;} else if (node2 == null) {return node1 != null ? node1.height : -1;}return -1;}請手動模擬哪里的高度需要改，哪里不需要改。
?
直觀表現程序
?
如果看的比較暈，或者直接從頭跳下來的同學，這個程序是正確的模擬了，維護AVL樹的策略和一些我沒寫的基本操作。大家可以自己操作，直觀感受一下。
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html?utm_source=qq&utm_medium=social&utm_oi=826801573962338304
?
跳表介紹和實現
?
想慢慢的給大家自然的引入跳表。
?
想想，我們
1）在有序數列里搜索一個數
2）或者把一個數插入到正確的位置
都怎么做？
很簡單吧
對于第一個操作，我們可以一個一個比較，在數組中我們可以二分，這樣比鏈表快
對于第二個操作，二分也沒什么用，因為找到位置還要在數組中一個一個挪位置，時間復雜度依舊是o(n)。
那我們怎么發明一個查找插入都比較快的結構呢？
?
?
?
可以打一些標記：
這樣我們把標記連起來，搜索一個數時先從標記開始搜起下一個標記比本身大的話就往下走，因為再往前就肯定不符合要求了。
比如我們要搜索18：
因為一次可以跨越好多數呀，自然快了一些。
既然可以打標記，我們可以改進一下，選出一些數來再打一層標記：
這樣我們搜索20是這樣的：
最終我們可以打好多層標記，我們從最高層開始搜索，一次可以跳過大量的數（依舊是右邊大了就往下走）。
比如搜索26：
最好的情況，就是每一層的標記都減少一半，這樣到了頂層往下搜索，其實和二分就沒什么兩樣，我們最底層用鏈表串起來，插入一個元素也不需要移動元素，所謂跳表就完成了一大半了。
?
現在的問題是，我們對于一個新數，到底應該給它打幾層標記呢？
（剛開始一個數都沒有，所以解決了這個問題，我們一直用這個策略更新即可）
答案是。。。。。投硬幣，全看臉。
我其實有點驚訝，我以為會有某些很強的和數學相關的算法，可以保證一個很好的搜索效率，是我想多了。
我們對于一個新數字，有一半概率可以打一層標記，有一半概率不可以打。
對于打了一層標記的數，我們依舊是這個方法，它有一半概率再向上打一層標記，依次循環。
所以每一層能到達的概率都少一半。
各層的節點數量竟然就可以比較好的維護在很好的效率上（最完美的就是達到了二分的效果）
?
再分析一下，其實對于同一個數字：
等等。。
其實沒必要全都用指針，因為我們知道，通過指針找到一個數可比下標慢多了。
所以同一個數字的所有標記，沒必要再用指針，效率低還不好維護，用一個list保存即可。
這樣，我們就設計出來一個數字的所有標記組成的結構：
public static class SkipListNode {public Integer value;//本身的值public ArrayList<SkipListNode> nextNodes;
//指向下一個元素的結點組成的數組，長度全看臉。public SkipListNode(Integer value) {this.value = value;nextNodes = new ArrayList<SkipListNode>();}}將integer比較的操作封裝一下：
private boolean lessThan(Integer a, Integer b) {return a.compareTo(b) < 0;}private boolean equalTo(Integer a, Integer b) {return a.compareTo(b) == 0;}找到在本層應該往下拐的結點：
// Returns the node at a given level with highest value less than eprivate SkipListNode findNext(Integer e, SkipListNode current, int level) {SkipListNode next = current.nextNodes.get(level);while (next != null) {Integer value = next.value;if (lessThan(e, value)) { // e < valuebreak;}current = next;next = current.nextNodes.get(level);}return current;}這樣我們就寫一個一層層往下找的方法，并且封裝成find(Integer e)的形式：
// Returns the skiplist node with greatest value <= eprivate SkipListNode find(Integer e) {return find(e, head, maxLevel);}// Returns the skiplist node with greatest value <= e// Starts at node start and levelprivate SkipListNode find(Integer e, SkipListNode current, int level) {do {current = findNext(e, current, level);} while (level-- > 0);return current;}剛才的方法是找到最大的小于等于目標的值，如果找到的值等于目標，跳表中就存在這個目標。否則不存在。
public boolean contains(Integer value) {SkipListNode node = find(value);return node != null && node.value != null && equalTo(node.value, value);}我們現在可以實現加入一個新點了，要注意把每層的標記打好：
public void add(Integer newValue) {if (!contains(newValue)) {size++;int level = 0;while (Math.random() < PROBABILITY) {level++;//能有幾層全看臉}while (level > maxLevel) {//大于當前最大層數head.nextNodes.add(null);//直接連系統最大maxLevel++;}SkipListNode newNode = new SkipListNode(newValue);SkipListNode current = head;//前一個結點，也就是說目標應插current之后do {//每一層往下走之前就可以設置這一層的標記了，就是鏈表插入一個新節點current = findNext(newValue, current, level);newNode.nextNodes.add(0, current.nextNodes.get(level));current.nextNodes.set(level, newNode);} while (level-- > 0);}}刪除也是一樣的
public void delete(Integer deleteValue) {if (contains(deleteValue)) {SkipListNode deleteNode = find(deleteValue);size--;int level = maxLevel;SkipListNode current = head;do {//就是一個鏈表刪除節點的操作current = findNext(deleteNode.value, current, level);if (deleteNode.nextNodes.size() > level) {current.nextNodes.set(level, deleteNode.nextNodes.get(level));}} while (level-- > 0);}}作為一個容器，Iterator那是必須有的吧，里面肯定有hasNext和next吧？
public static class SkipListIterator implements Iterator<Integer> {SkipList list;SkipListNode current;public SkipListIterator(SkipList list) {this.list = list;this.current = list.getHead();}public boolean hasNext() {return current.nextNodes.get(0) != null;}public Integer next() {current = current.nextNodes.get(0);return current.value;}}這個跳表我們就實現完了。
現實工作中呢，我們一般不會讓它到無限多層，萬一有一個數它人氣爆炸隨機數沖到了一萬層呢？
所以包括redis在內的一些跳表實現，都是規定了一個最大層數的。
別的好像也沒什么了。
最后貼出所有代碼。
import java.util.ArrayList;
import java.util.Iterator;public SkipListDemo {public static class SkipListNode {public Integer value;public ArrayList<SkipListNode> nextNodes;public SkipListNode(Integer value) {this.value = value;nextNodes = new ArrayList<SkipListNode>();}}public static class SkipListIterator implements Iterator<Integer> {SkipList list;SkipListNode current;public SkipListIterator(SkipList list) {this.list = list;this.current = list.getHead();}public boolean hasNext() {return current.nextNodes.get(0) != null;}public Integer next() {current = current.nextNodes.get(0);return current.value;}}public static class SkipList {private SkipListNode head;private int maxLevel;private int size;private static final double PROBABILITY = 0.5;public SkipList() {size = 0;maxLevel = 0;head = new SkipListNode(null);head.nextNodes.add(null);}public SkipListNode getHead() {return head;}public void add(Integer newValue) {if (!contains(newValue)) {size++;int level = 0;while (Math.random() < PROBABILITY) {level++;}while (level > maxLevel) {head.nextNodes.add(null);maxLevel++;}SkipListNode newNode = new SkipListNode(newValue);SkipListNode current = head;do {current = findNext(newValue, current, level);newNode.nextNodes.add(0, current.nextNodes.get(level));current.nextNodes.set(level, newNode);} while (level-- > 0);}}public void delete(Integer deleteValue) {if (contains(deleteValue)) {SkipListNode deleteNode = find(deleteValue);size--;int level = maxLevel;SkipListNode current = head;do {current = findNext(deleteNode.value, current, level);if (deleteNode.nextNodes.size() > level) {current.nextNodes.set(level, deleteNode.nextNodes.get(level));}} while (level-- > 0);}}// Returns the skiplist node with greatest value <= eprivate SkipListNode find(Integer e) {return find(e, head, maxLevel);}// Returns the skiplist node with greatest value <= e// Starts at node start and levelprivate SkipListNode find(Integer e, SkipListNode current, int level) {do {current = findNext(e, current, level);} while (level-- > 0);return current;}// Returns the node at a given level with highest value less than eprivate SkipListNode findNext(Integer e, SkipListNode current, int level) {SkipListNode next = current.nextNodes.get(level);while (next != null) {Integer value = next.value;if (lessThan(e, value)) { // e < valuebreak;}current = next;next = current.nextNodes.get(level);}return current;}public int size() {return size;}public boolean contains(Integer value) {SkipListNode node = find(value);return node != null && node.value != null && equalTo(node.value, value);}public Iterator<Integer> iterator() {return new SkipListIterator(this);}/******************************************************************************* Utility Functions *******************************************************************************/private boolean lessThan(Integer a, Integer b) {return a.compareTo(b) < 0;}private boolean equalTo(Integer a, Integer b) {return a.compareTo(b) == 0;}}public static void main(String[] args) {}}c語言實現排序和查找所有算法
?
?c語言版排序查找完成，帶詳細解釋，一下看到爽，能直接運行看效果。
?
/* Note:Your choice is C IDE */
#include "stdio.h"
#include"stdlib.h"
#define MAX 10
void SequenceSearch(int *fp,int Length);
void Search(int *fp,int length);
void Sort(int *fp,int length);
/*
注意：1、數組名x,*(x+i)就是x[i]哦*//*
================================================
功能:選擇排序
輸入:數組名稱(數組首地址)、數組中元素個數
================================================
*/
void select_sort(int *x, int n)
{int i, j, min, t;for (i=0; i<n-1; i++) /*要選擇的次數:下標：0~n-2，共n-1次*/{min = i; /*假設當前下標為i的數最小,比較后再調整*/for (j=i+1; j<n; j++)/*循環找出最小的數的下標是哪個*/{if (*(x+j) < *(x+min))min = j; /*如果后面的數比前面的小,則記下它的下標*/}if (min != i) /*如果min在循環中改變了,就需要交換數據*/{t = *(x+i);*(x+i) = *(x+min);*(x+min) = t;}}
}
/*
================================================
功能:直接插入排序
輸入:數組名稱(也就是數組首地址)、數組中元素個數
================================================
*/void insert_sort(int *x, int n)
{int i, j, t;for (i=1; i<n; i++) /*要選擇的次數:下標1~n-1，共n-1次*/{/*暫存下標為i的數。注意:下標從1開始,原因就是開始時第一個數即下標為0的數,前面沒有任何數,認為它是排好順序的。*/t=*(x+i);for (j=i-1; j>=0 && t<*(x+j); j--) /*注意:j=i-1,j--,這里就是下標為i的數,在它前面有序列中找插入位置。*/{*(x+j+1) = *(x+j); /*如果滿足條件就往后挪。最壞的情況就是t比下標為0的數都小,它要放在最前面,j==-1,退出循環*/}*(x+j+1) = t; /*找到下標為i的數的放置位置*/}
}
/*
================================================
功能:冒泡排序
輸入:數組名稱(也就是數組首地址)、數組中元素個數
================================================
*/
void bubble_sort0(int *x, int n)
{int j, h, t;for (h=0; h<n-1; h++)/*循環n-1次*/{for (j=0; j<n-2-h; j++)/*每次做的操作類似*/{if (*(x+j) > *(x+j+1)) /*大的放在后面,小的放到前面*/{t = *(x+j);*(x+j) = *(x+j+1);*(x+j+1) = t; /*完成交換*/}}}
}
/*優化：記錄最后下沉位置，之后的肯定有序*/
void bubble_sort(int *x, int n)
{int j, k, h, t;for (h=n-1; h>0; h=k) /*循環到沒有比較范圍*/{for (j=0, k=0; j<h; j++) /*每次預置k=0,循環掃描后更新k*/{if (*(x+j) > *(x+j+1)) /*大的放在后面,小的放到前面*/{t = *(x+j);*(x+j) = *(x+j+1);*(x+j+1) = t; /*完成交換*/k = j; /*保存最后下沉的位置。這樣k后面的都是排序排好了的。*/}}}
}
/*
================================================
功能:希爾排序
輸入:數組名稱(也就是數組首地址)、數組中元素個數
================================================
*/void shell_sort(int *x, int n)
{int h, j, k, t;for (h=n/2; h>0; h=h/2) /*控制增量*/{for (j=h; j<n; j++) /*這個實際上就是上面的直接插入排序*/{t = *(x+j);for (k=j-h; (k>=0 && t<*(x+k)); k-=h){*(x+k+h) = *(x+k);}*(x+k+h) = t;}}
}
/*
================================================
功能:快速排序
輸入:數組名稱(也就是數組首地址)、數組中起止元素的下標
注：自己畫畫
================================================
*/void quick_sort(int *x, int low, int high)
{int i, j, t;if (low < high) /*要排序的元素起止下標,保證小的放在左邊,大的放在右邊。這里以下標為low的元素（最左邊）為基準點*/{i = low;j = high;t = *(x+low); /*暫存基準點的數*/while (i<j) /*循環掃描*/{while (i<j && *(x+j)>t) /*在右邊的只要比基準點大仍放在右邊*/{j--; /*前移一個位置*/}if (i<j){*(x+i) = *(x+j); /*上面的循環退出:即出現比基準點小的數,替換基準點的數*/i++; /*后移一個位置,并以此為基準點*/}while (i<j && *(x+i)<=t) /*在左邊的只要小于等于基準點仍放在左邊*/{i++; /*后移一個位置*/}if (i<j){*(x+j) = *(x+i); /*上面的循環退出:即出現比基準點大的數,放到右邊*/j--; /*前移一個位置*/}}*(x+i) = t; /*一遍掃描完后,放到適當位置*/quick_sort(x,low,i-1); /*對基準點左邊的數再執行快速排序*/quick_sort(x,i+1,high); /*對基準點右邊的數再執行快速排序*/}
}
/*
================================================
功能:堆排序
輸入:數組名稱(也就是數組首地址)、數組中元素個數
注：畫畫
================================================
*/
/*
功能:建堆
輸入:數組名稱(也就是數組首地址)、參與建堆元素的個數、從第幾個元素開始
*/
void sift(int *x, int n, int s)
{int t, k, j;t = *(x+s); /*暫存開始元素*/k = s; /*開始元素下標*/j = 2*k + 1; /*左子樹元素下標*/while (j<n){if (j<n-1 && *(x+j) < *(x+j+1))/*判斷是否存在右孩子，并且右孩子比左孩子大，成立，就把j換為右孩子*/{j++;}if (t<*(x+j)) /*調整*/{*(x+k) = *(x+j);k = j; /*調整后,開始元素也隨之調整*/j = 2*k + 1;}else /*沒有需要調整了,已經是個堆了,退出循環。*/{break;}}*(x+k) = t; /*開始元素放到它正確位置*/
}
/*
功能:堆排序
輸入:數組名稱(也就是數組首地址)、數組中元素個數
注：** ** - * ** * *
建堆時，從從后往前第一個非葉子節點開始調整，也就是“-”符號的位置
*/
void heap_sort(int *x, int n)
{int i, k, t;
//int *p;for (i=n/2-1; i>=0; i--){sift(x,n,i); /*初始建堆*/}for (k=n-1; k>=1; k--){t = *(x+0); /*堆頂放到最后*/*(x+0) = *(x+k);*(x+k) = t;sift(x,k,0); /*剩下的數再建堆*/}
}// 歸并排序中的合并算法
void Merge(int a[], int start, int mid, int end)
{int i,k,j, temp1[10], temp2[10];int n1, n2;n1 = mid - start + 1;n2 = end - mid;// 拷貝前半部分數組for ( i = 0; i < n1; i++){temp1[i] = a[start + i];}// 拷貝后半部分數組for (i = 0; i < n2; i++){temp2[i] = a[mid + i + 1];}// 把后面的元素設置的很大temp1[n1] = temp2[n2] = 1000;// 合并temp1和temp2for ( k = start, i = 0, j = 0; k <= end; k++){//小的放到有順序的數組里if (temp1[i] <= temp2[j]){a[k] = temp1[i];i++;}else{a[k] = temp2[j];j++;}}
}// 歸并排序
void MergeSort(int a[], int start, int end)
{if (start < end){int i;i = (end + start) / 2;// 對前半部分進行排序MergeSort(a, start, i);// 對后半部分進行排序MergeSort(a, i + 1, end);// 合并前后兩部分Merge(a, start, i, end);}
}
/*順序查找*/
void SequenceSearch(int *fp,int Length)
{int i;int data;printf("開始使用順序查詢.\n請輸入你想要查找的數據.\n");scanf("%d",&data);for(i=0; i<Length; i++)if(fp[i]==data){printf("經過%d次查找,查找到數據%d,表中位置為%d.\n",i+1,data,i);return ;}printf("經過%d次查找,未能查找到數據%d.\n",i,data);
}
/*二分查找*/
void Search(int *fp,int Length)
{int data;int bottom,top,middle;int i=0;printf("開始使用二分查詢.\n請輸入你想要查找的數據.\n");scanf("%d",&data);printf("由于二分查找法要求數據是有序的,現在開始為數組排序.\n");Sort(fp,Length);printf("數組現在已經是從小到大排列,下面將開始查找.\n");bottom=0;top=Length;while (bottom<=top){middle=(bottom+top)/2;i++;if(fp[middle]<data){bottom=middle+1;}else if(fp[middle]>data){top=middle-1;}else{printf("經過%d次查找,查找到數據%d,在排序后的表中的位置為%d.\n",i,data,middle);return;}}printf("經過%d次查找,未能查找到數據%d.\n",i,data);
}/*下面測試了*/
void Sort(int *fp,int Length)
{int temp;int i,j,k;printf("現在開始為數組排序,排列結果將是從小到大.\n");for(i=0; i<Length; i++)for(j=0; j<Length-i-1; j++)if(fp[j]>fp[j+1]){temp=fp[j];fp[j]=fp[j+1];fp[j+1]=temp;}printf("排序完成!\n下面輸出排序后的數組:\n");for(k=0; k<Length; k++){printf("%5d",fp[k]);}printf("\n");}
/*構造隨機輸出函數類*/
void input(int a[])
{int i;srand( (unsigned int)time(NULL) );for (i = 0; i < 10; i++){a[i] = rand() % 100;}printf("\n");
}
/*構造鍵盤輸入函數類*/
/*void input(int *p)
{int i;printf("請輸入 %d 個數據 :\n",MAX);for (i=0; i<MAX; i++){scanf("%d",p++);}printf("\n");
}*/
/*構造輸出函數類*/
void output(int *p)
{int i;for ( i=0; i<MAX; i++){printf("%d ",*p++);}
}
void main()
{int start=0,end=3;int *p, i, a[MAX];int count=MAX;int arr[MAX];int choise=0;/*printf("請輸入你的數據的個數:\n");scanf("%d",&count);*//* printf("請輸入%d個數據\n",count);for(i=0;i<count;i++){scanf("%d",&arr[i]);}*//*錄入測試數據*/input(a);printf("隨機初始數組為：\n");output(a);printf("\n");do{printf("1.使用順序查詢.\n2.使用二分查找法查找.\n3.退出\n");scanf("%d",&choise);if(choise==1)SequenceSearch(a,count);else if(choise==2)Search(a,count);else if(choise==3)break;}while (choise==1||choise==2||choise==3);/*錄入測試數據*/input(a);printf("隨機初始數組為：\n");output(a);printf("\n");/*測試選擇排序*/p = a;printf("選擇排序之后的數據:\n");select_sort(p,MAX);output(a);printf("\n");system("pause");/**//*錄入測試數據*/input(a);printf("隨機初始數組為：\n");output(a);printf("\n");/*測試直接插入排序*/printf("直接插入排序之后的數據:\n");p = a;insert_sort(p,MAX);output(a);printf("\n");system("pause");/*錄入測試數據*/input(a);printf("隨機初始數組為：\n");output(a);printf("\n");/*測試冒泡排序*/printf("冒泡排序之后的數據:\n");p = a;insert_sort(p,MAX);output(a);printf("\n");system("pause");/*錄入測試數據*/input(a);printf("隨機初始數組為：\n");output(a);printf("\n");/*測試快速排序*/printf("快速排序之后的數據:\n");p = a;quick_sort(p,0,MAX-1);output(a);printf("\n");system("pause");/*錄入測試數據*/input(a);printf("隨機初始數組為：\n");output(a);printf("\n");/*測試堆排序*/printf("堆排序之后的數據:\n");p = a;heap_sort(p,MAX);output(a);printf("\n");system("pause");/*錄入測試數據*/input(a);printf("隨機初始數組為：\n");output(a);printf("\n");/*測試歸并排序*/printf("歸并排序之后的數據:\n");p = a;MergeSort(a,start,end);output(a);printf("\n");system("pause");
}?
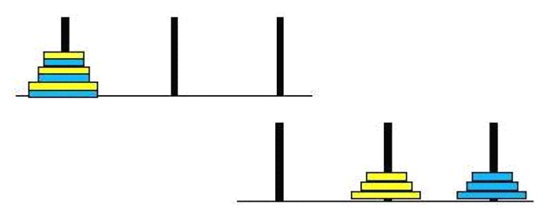
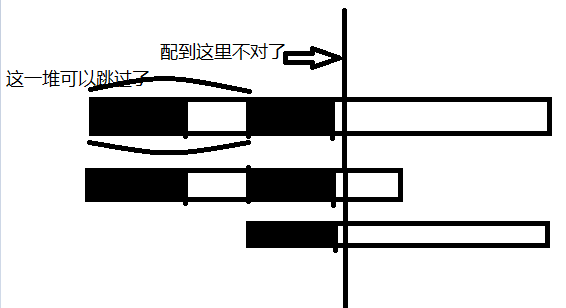
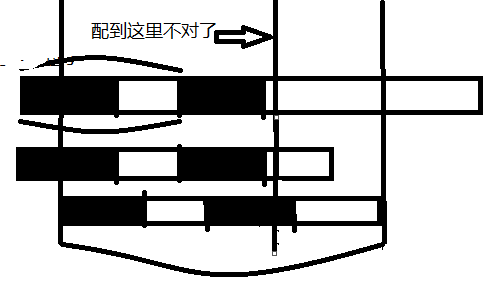
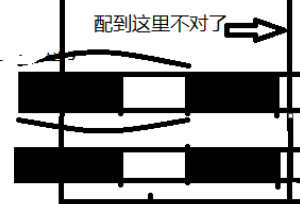
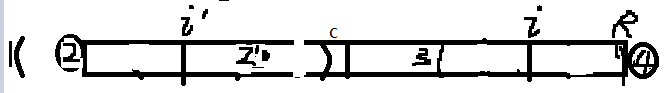
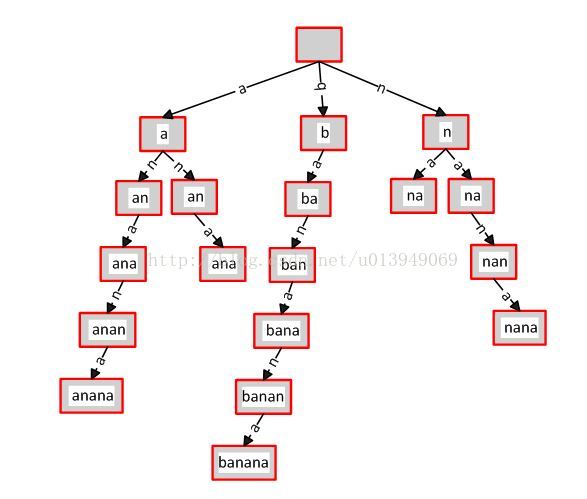
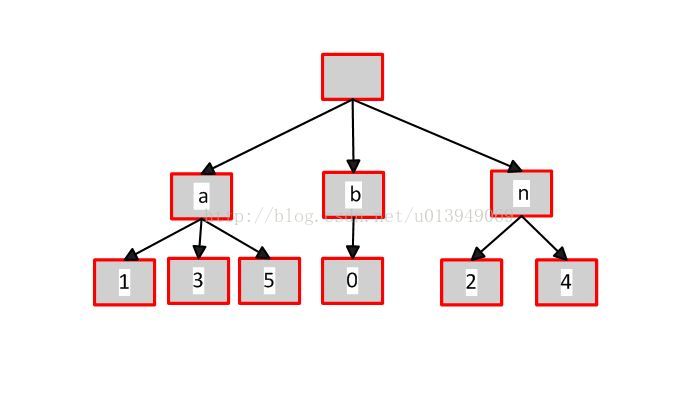
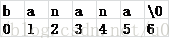
方法、apply()方法】)
