目錄
數據結構的圖存儲結構
圖存儲結構基本常識
弧頭和弧尾
入度和出度
(V1,V2) 和 的區別,v2>
集合 VR 的含義
路徑和回路
權和網的含義
圖存儲結構的分類
什么是連通圖,(強)連通圖詳解
強連通圖
什么是生成樹,生成樹(生成森林)詳解
生成森林
數據結構的圖存儲結構
我們知道,數據之間的關系有 3 種,分別是 "一對一"、"一對多" 和 "多對多",前兩種關系的數據可分別用線性表和樹結構存儲,本節學習存儲具有"多對多"邏輯關系數據的結構——圖存儲結構。
?
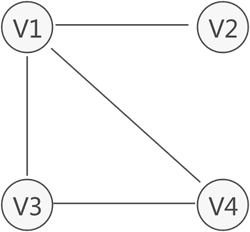
圖 1 圖存儲結構示意圖
圖 1 所示為存儲 V1、V2、V3、V4 的圖結構,從圖中可以清楚的看出數據之間具有的"多對多"關系。例如,V1 與 V4 和 V2 建立著聯系,V4 與 V1 和 V3 建立著聯系,以此類推。
與鏈表不同,圖中存儲的各個數據元素被稱為頂點(而不是節點)。拿圖 1 來說,該圖中含有 4 個頂點,分別為頂點 V1、V2、V3 和 V4。
圖存儲結構中,習慣上用 Vi 表示圖中的頂點,且所有頂點構成的集合通常用 V 表示,如圖 1 中頂點的集合為 V={V1,V2,V3,V4}。
注意,圖 1 中的圖僅是圖存儲結構的其中一種,數據之間 "多對多" 的關系還可能用如圖 2 所示的圖結構表示:
?
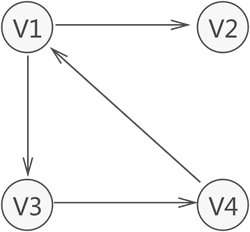
圖 2 有向圖示意圖
可以看到,各個頂點之間的關系并不是"雙向"的。比如,V4 只與 V1 存在聯系(從 V4 可直接找到 V1),而與 V3 沒有直接聯系;同樣,V3 只與 V4 存在聯系(從 V3 可直接找到 V4),而與 V1 沒有直接聯系,以此類推。
因此,圖存儲結構可細分兩種表現類型,分別為無向圖(圖 1)和有向圖(圖 2)。
圖存儲結構基本常識
弧頭和弧尾
有向圖中,無箭頭一端的頂點通常被稱為"初始點"或"弧尾",箭頭直線的頂點被稱為"終端點"或"弧頭"。
入度和出度
對于有向圖中的一個頂點 V 來說,箭頭指向 V 的弧的數量為 V 的入度(InDegree,記為 ID(V));箭頭遠離 V 的弧的數量為 V 的出度(OutDegree,記為OD(V))。拿圖 2 中的頂點 V1來說,該頂點的入度為 1,出度為 2(該頂點的度為 3)。
(V1,V2) 和 <V1,V2> 的區別
無向圖中描述兩頂點(V1 和 V2)之間的關系可以用 (V1,V2) 來表示,
而有向圖中描述從 V1 到 V2 的"單向"關系用 <V1,V2> 來表示。
由于圖存儲結構中頂點之間的關系是用線來表示的,因此 (V1,V2) 還可以用來表示無向圖中連接 V1 和 V2 的線,又稱為邊;同樣,<V1,V2> 也可用來表示有向圖中從 V1 到 V2 帶方向的線,又稱為弧。
集合 VR 的含義
并且,圖中習慣用 VR 表示圖中所有頂點之間關系的集合。例如,圖 1 中無向圖的集合 VR={(v1,v2),(v1,v4),(v1,v3),(v3,v4)},圖 2 中有向圖的集合 VR={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}。
路徑和回路
無論是無向圖還是有向圖,從一個頂點到另一頂點途徑的所有頂點組成的序列(包含這兩個頂點),稱為一條路徑。如果路徑中第一個頂點和最后一個頂點相同,則此路徑稱為"回路"(或"環")。
并且,若路徑中各頂點都不重復,此路徑又被稱為"簡單路徑";同樣,若回路中的頂點互不重復,此回路被稱為"簡單回路"(或簡單環)。
拿圖 1 來說,從 V1 存在一條路徑還可以回到 V1,此路徑為 {V1,V3,V4,V1},這是一個回路(環),而且還是一個簡單回路(簡單環)。
在有向圖中,每條路徑或回路都是有方向的。
權和網的含義
在某些實際場景中,圖中的每條邊(或弧)會賦予一個實數來表示一定的含義,這種與邊(或弧)相匹配的實數被稱為"權",而帶權的圖通常稱為網。如圖 3 所示,就是一個網結構:
?
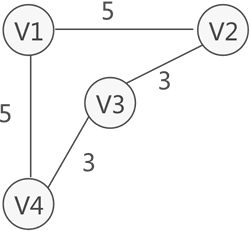
圖 3 帶權的圖存儲結構
子圖:指的是由圖中一部分頂點和邊構成的圖,稱為原圖的子圖。
圖存儲結構的分類
根據不同的特征,圖又可分為完全圖,連通圖、稀疏圖和稠密圖:
完全圖:若圖中各個頂點都與除自身外的其他頂點有關系,這樣的無向圖稱為完全圖(如圖 4a))。同時,滿足此條件的有向圖則稱為有向完全圖(圖 4b))。
?
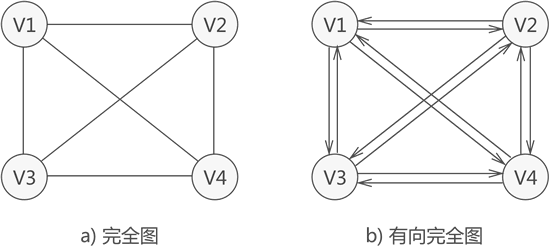
圖 4 完全圖示意圖
具有 n 個頂點的完全圖,圖中邊的數量為 n(n-1)/2;
對于具有 n 個頂點的有向完全圖,圖中弧的數量為 n(n-1)。
- 稀疏圖和稠密圖:這兩種圖是相對存在的,即如果圖中具有很少的邊(或弧),此圖就稱為"稀疏圖";反之,則稱此圖為"稠密圖"。
稀疏和稠密的判斷條件是:e<nlogn,其中 e 表示圖中邊(或弧)的數量,n 表示圖中頂點的數量。如果式子成立,則為稀疏圖;反之為稠密圖。
什么是連通圖,(強)連通圖詳解
前面講過,圖中從一個頂點到達另一頂點,若存在至少一條路徑,則稱這兩個頂點是連通著的。例如圖 1 中,雖然 V1 和 V3 沒有直接關聯,但從 V1 到 V3 存在兩條路徑,分別是?V1-V2-V3?和?V1-V4-V3,因此稱 V1 和 V3 之間是連通的。
?
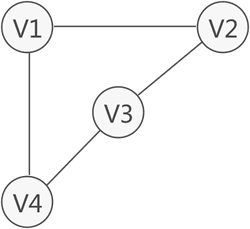
圖 1 頂點之間的連通狀態示意圖
無向圖中,如果任意兩個頂點之間都能夠連通,則稱此無向圖為連通圖。例如,圖 2 中的無向圖就是一個連通圖,因為此圖中任意兩頂點之間都是連通的。
?
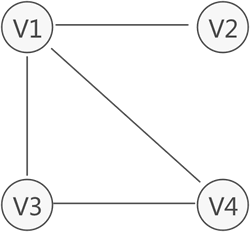
圖 2 連通圖示意圖
若無向圖不是連通圖,但圖中存儲某個子圖符合連通圖的性質,則稱該子圖為連通分量。
前面講過,由圖中部分頂點和邊構成的圖為該圖的一個子圖,但這里的子圖指的是圖中"最大"的連通子圖(也稱"極大連通子圖")。
如圖 3 所示,雖然圖 3a) 中的無向圖不是連通圖,但可以將其分解為 3 個"最大子圖"(圖 3b)),它們都滿足連通圖的性質,因此都是連通分量。
?
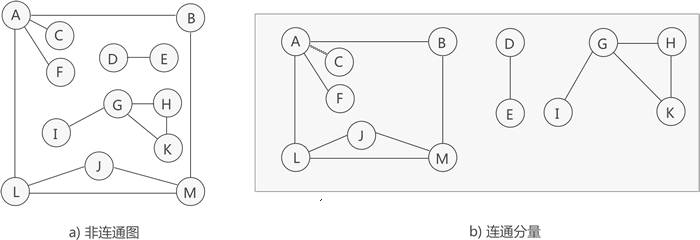
圖 3 連通分量示意圖
提示,圖 3a) 中的無向圖只能分解為 3 部分各自連通的"最大子圖"。
需要注意的是,連通分量的提出是以"整個無向圖不是連通圖"為前提的,因為如果無向圖是連通圖,則其無法分解出多個最大連通子圖,因為圖中所有的頂點之間都是連通的。
強連通圖
有向圖中,若任意兩個頂點 Vi 和 Vj,滿足從 Vi 到 Vj 以及從 Vj 到 Vi 都連通,也就是都含有至少一條通路,則稱此有向圖為強連通圖。如圖 4 所示就是一個強連通圖。
?
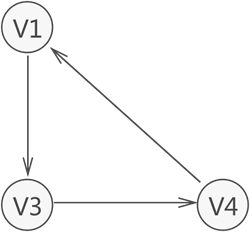
圖 4 強連通圖
與此同時,若有向圖本身不是強連通圖,但其包含的最大連通子圖具有強連通圖的性質,則稱該子圖為強連通分量。
?
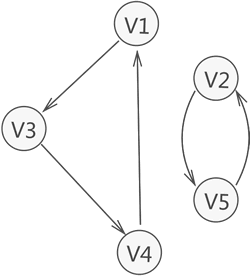
圖 5 強連通分量
如圖 5 所示,整個有向圖雖不是強連通圖,但其含有兩個強連通分量。
可以這樣說,連通圖是在無向圖的基礎上對圖中頂點之間的連通做了更高的要求,而強連通圖是在有向圖的基礎上對圖中頂點的連通做了更高的要求。
什么是生成樹,生成樹(生成森林)詳解
對連通圖進行遍歷,過程中所經過的邊和頂點的組合可看做是一棵普通樹,通常稱為生成樹。
?
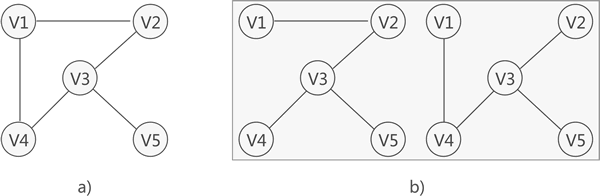
圖 1 連通圖及其對應的生成樹
如圖 1 所示,圖 1a) 是一張連通圖,圖 1b) 是其對應的 2 種生成樹。
連通圖中,由于任意兩頂點之間可能含有多條通路,遍歷連通圖的方式有多種,往往一張連通圖可能有多種不同的生成樹與之對應。
連通圖中的生成樹必須滿足以下 2 個條件:
- 包含連通圖中所有的頂點;
- 任意兩頂點之間有且僅有一條通路;
因此,連通圖的生成樹具有這樣的特征,即生成樹中邊的數量 = 頂點數 - 1。
生成森林
生成樹是對應連通圖來說
而生成森林是對應非連通圖來說的。
我們知道,非連通圖可分解為多個連通分量,而每個連通分量又各自對應多個生成樹(至少是 1 棵),因此與整個非連通圖相對應的,是由多棵生成樹組成的生成森林。
?
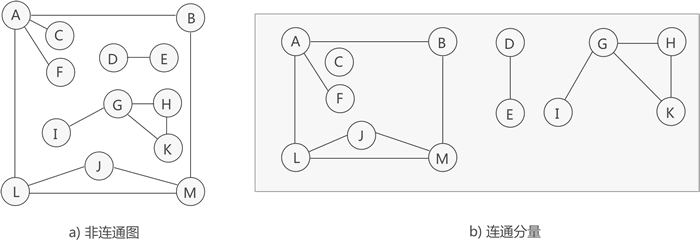
圖 2 非連通圖和連通分量
如圖 2 所示,這是一張非連通圖,可分解為 3 個連通分量,其中各個連通分量對應的生成樹如圖 3 所示:
?
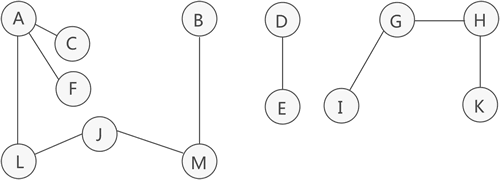
圖 3 生成森林
注意,圖 3 中列出的僅是各個連通分量的其中一種生成樹。
因此,多個連通分量對應的多棵生成樹就構成了整個非連通圖的生成森林。





)



)
四(116))







)
