1 想法概述

從一張充滿噪聲的圖中不斷denoise，最終得到一張clear的圖片。為了確定當前圖片中噪聲占比的大小，同時輸入原圖片和參數$t$，參數$t$用于標識一張圖片中的噪聲占比含量。

顯然迭代第1次時圖片的噪聲含量和迭代第999次是不同的，因此需要輸入這種信息t來進行標識。

2 實際過程

階段1 Add Noise

首先，準備好一組確定的參數$\overline{{\alpha }_1},\overline{{\alpha }_2},\dots ,\overline{{\alpha }_T}$，用以表示時間步$t$下樣本和噪聲的混合情況，$t$越大，噪聲占比越高。然后重復以下過程直至收斂：

1. 采樣

   1. 從真實樣本集中取出一個樣本$x_0$

   2. 從$[1,T]$的整數中采樣出$t$來表示時間步

   3. 從標準正態分布中采樣出噪聲$?$

2. 構造帶噪聲樣本$x=\sqrt{\overline{{\alpha }_t}}{x}_0+\sqrt{1?\overline{{\alpha }_t}}?$

3. 將構造樣本$x$和時間步$t$一同輸入噪聲預測器${?}_{\theta }()$，得到預測噪聲${?}_{\theta }(x,t)$。

4. 目標函數為${?}_{\theta }(x,t)$和采樣出的真實噪聲$?$的$MSE$

階段2 Denoise

3 數學原理

1. 極大似然估計近似等價于最小化KL散度(表示兩個分布的相似性)：

2. 對任何分布$q(z|x)$，有：

$$\log P_{\theta }(x)\ge {\int }_{z}q(z|x)\log \frac{P(z,x)}{q(z|x)}dz=E_{q(z|x)}[\log \frac{P(z,x)}{q(z|x)}]$$

3. 所以對DDPM來說：

$$\log P_{\theta }(x)\ge E_{q(x_1:x_T|x_0)}[\log \frac{P(x_0:x_T)}{q(x_1:x_T|x_0)}]$$

4. 結合正態分布的可加性：做N次獨立的正態sampling，可能通過一次的sampling就能解決。

5. 對式3不斷變換，最后可得（這個式子的過程可以不用看，也并不復雜，但是麻煩，理解結論就好）：

然后再經過一系列的運算求出來$q(x_{t?1|x_t,x_0})$依然是高斯分布，表示首尾$x_0,x_T$固定住，產生$x_{t?1}$的概率，是一個和network無關的分布。而$P(x_{t?1}|x_t)$是由網絡決定的，我們不考慮它的variance，只考慮mean。如果我們希望這兩個分布越接近越好，那就想辦法讓兩個分布的mean越接近越好。

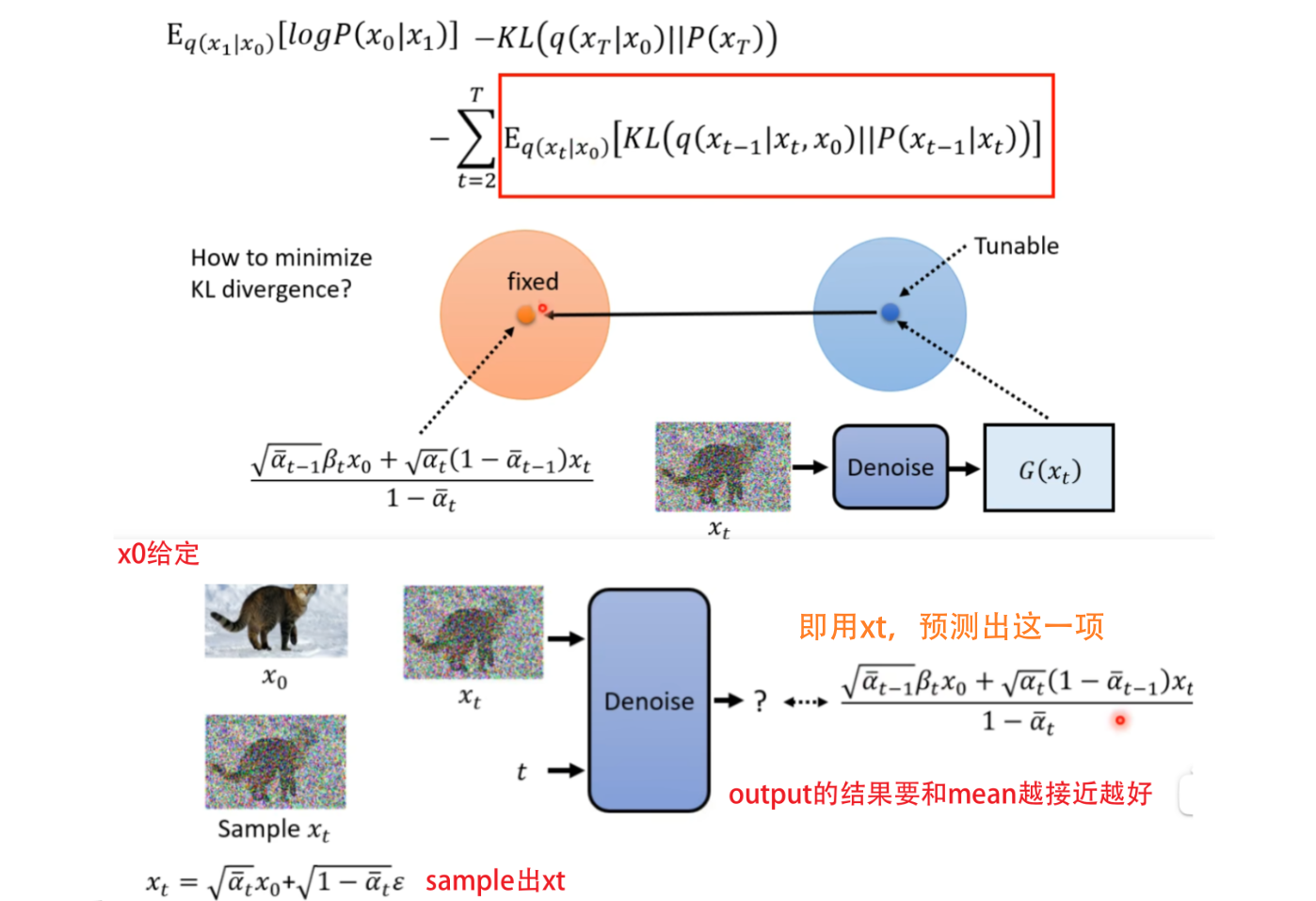
化簡：

實際需要預測出的部分：

4 為什么推理時要額外加入noise

李宏毅老師的一點Guess，生成式任務，概率最大的結果，未必就是最好的結果。人寫的文章用詞可能更suprising。

5 一些不知道對不對的Summary

• 希望近似$P_{data}(x)$和$P_{\theta }(x)$的分布，而對給定的$x$，使$P_{\theta }(x)$最大化可以轉換為使其下界最大化，從而轉換為使$E_{q(x_1:x_T|x_0)}[\log \frac{P(x_0:x_T)}{q(x_1:x_T|x_0)}]$最大化。

• 在假設$x_t=\sqrt{{\beta }_t}{x}_{t?1}+\sqrt{1?{\beta }_t}{z}_{t?1}$的前提下，可以推出$x_t=\sqrt{\overline{{\alpha }_t}}{x}_0+\sqrt{1?\overline{{\alpha }_t}}z$

• 從而可以進一步化簡$E_{q(x_1:x_T|x_0)}[\log \frac{P(x_0:x_T)}{q(x_1:x_T|x_0)}]$為三項，其余兩項與Network無關，可只考慮中間一項，該項由$q(x_{t?1|x_t,x_0})$和$P(x_{t?1}|x_t)$的KL散度之和組成，

• $q(x_{t?1}|x_t,x_0)$表示首尾$x_0,x_T$固定住產生$x_{t?1}$的概率，可求得是一個和network無關的高斯分布，均值可以表示為：

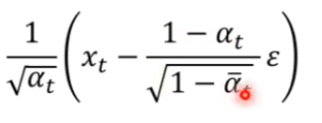
• 而$P(x_{t?1}|x_t)$是由網絡決定的，我們不考慮它的variance，只考慮mean。

• 如果我們希望這兩個分布越接近越好，那就想辦法讓兩個分布的mean越接近越好。而上式中，僅有$?$需要確定，因此我們希望網絡能夠預測這個值，從而完成推理。預測出這一項$?$的過程，可以看作為從$x_0$和$x_t$預測出$x_{t?1}$的過程。