【算法學習】兩數之和II - 輸入有序數組

題目描述

原題鏈接

給你一個下標從 1 開始的整數數組 numbers ，該數組已按 非遞減順序排列 ，請你從數組中找出滿足相加之和等于目標數 target 的兩個數。如果設這兩個數分別是 numbers[index1] 和 numbers[index2] ，則 1 <= index1 < index2 <= numbers.length 。

以長度為 2 的整數數組 [index1, index2] 的形式返回這兩個整數的下標 index1 和 index2。

你可以假設每個輸入 只對應唯一的答案 ，而且你 不可以 重復使用相同的元素。

你所設計的解決方案必須只使用常量級的額外空間。

示例 1：

輸入：numbers = [2,7,11,15], target = 9
輸出：[1,2]
解釋： 2 與 7 之和等于目標數 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

輸入：numbers = [2,3,4], target = 6
輸出：[1,3]
解釋：2 與 4 之和等于目標數 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

輸入：numbers = [-1,0], target = -1
輸出：[1,2]
解釋：-1 與 0 之和等于目標數 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

提示：

2 <= numbers.length <= 3 * 104
-1000 <= numbers[i] <= 1000
numbers 按 非遞減順序 排列
-1000 <= target <= 1000
僅存在一個有效答案

雙指針法

思路分析

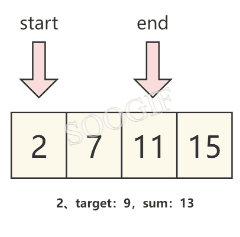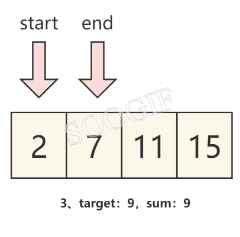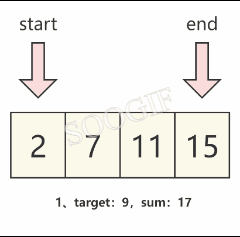
我們觀察題目可以發現，數組是已經排好序的，那么我們可以直接定義兩個元素來分別指向 數組頭 和 數組尾 ，然后循環使兩個指針移動，直到最終算出我們需要的結果。

假設左指針為start，右指針為end，并將左右指針所對應的元素的和設為sum，那么我們就可以發現：

當 sum==target 時，就可以得到我們需要的結果
當 sum>target 時，我們需要將右指針對應的元素變小一些，那么就需要 將右指針向左移動一個元素，也就是 end--
當 sum<target 時，我們需要將左指針對應的元素變大一些，那么就需要 將左指針向右移動一個元素，也就是 start++

我們可以通過下圖來理解這個規律。

圖解

雙指針法.gif

代碼實現

public int[] twoSum(int[] numbers, int target) {if (null == numbers) {return new int[0];}int start = 0;int end = numbers.length - 1;while (start < end) {int sum = numbers[start] + numbers[end];if (sum == target) {return new int[]{start + 1, end + 1};} else if (sum > target) {end--;} else {start++;}}return new int[0];
}

二分查找法

思路分析

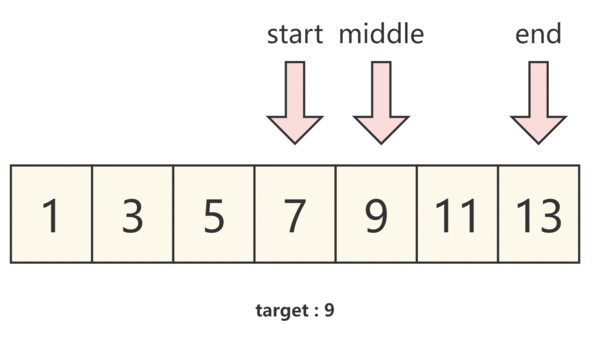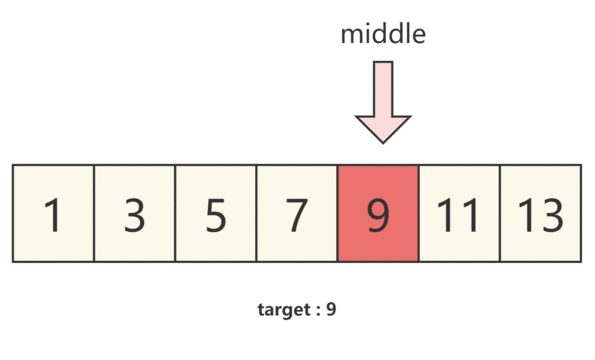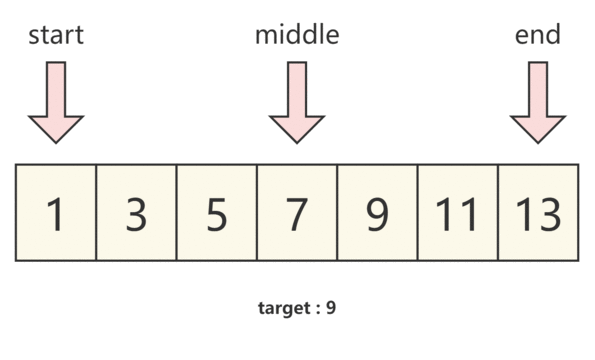
那么我們將題目帶入，假設左指針為 start，右指針為 end，并將左右指針中間的下標為 middle，即可得到：

當 numbers[middle]==target 時，我們即可得到需要的結果
當 numbers[middle]>target 時，說明 中間數大于預期結果，結果在左半部分，那么我們需要 將右指針移動至middle的位置，并重新取middle的位置。
當 numbers[middle]<target 時，說明 中間數小于預期結果，結果在右半部分，那么我們需要 將左指針移動至middle的位置，并重新取middle的位置。

我們通過下圖來理解。

圖解

代碼實現

public int[] twoSum(int[] numbers, int target) {if (null == numbers) {return new int[0];}for (int i = 0; i < numbers.length; ++i) {int start = i + 1;int end = numbers.length - 1;while (start <= end) {int middle = (end - start) / 2 + start;if (numbers[middle] == target - numbers[i]) {return new int[]{i + 1, middle + 1};} else if (numbers[middle] > target - numbers[i]) {end = middle - 1;} else {start = middle + 1;}}}return new int[0];}