一、簡介

SVM是一種二類分類模型，在特征空間中尋找間隔最大的分離超平面，使得數據得到高效的二分類。

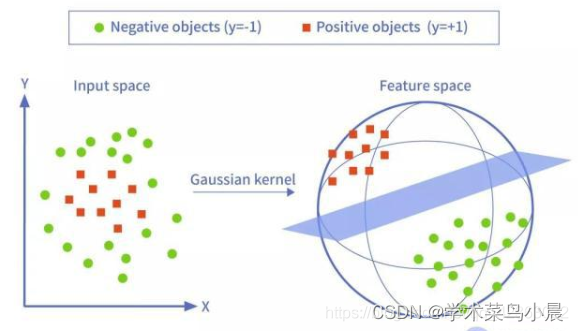
?二、SVM損失函數

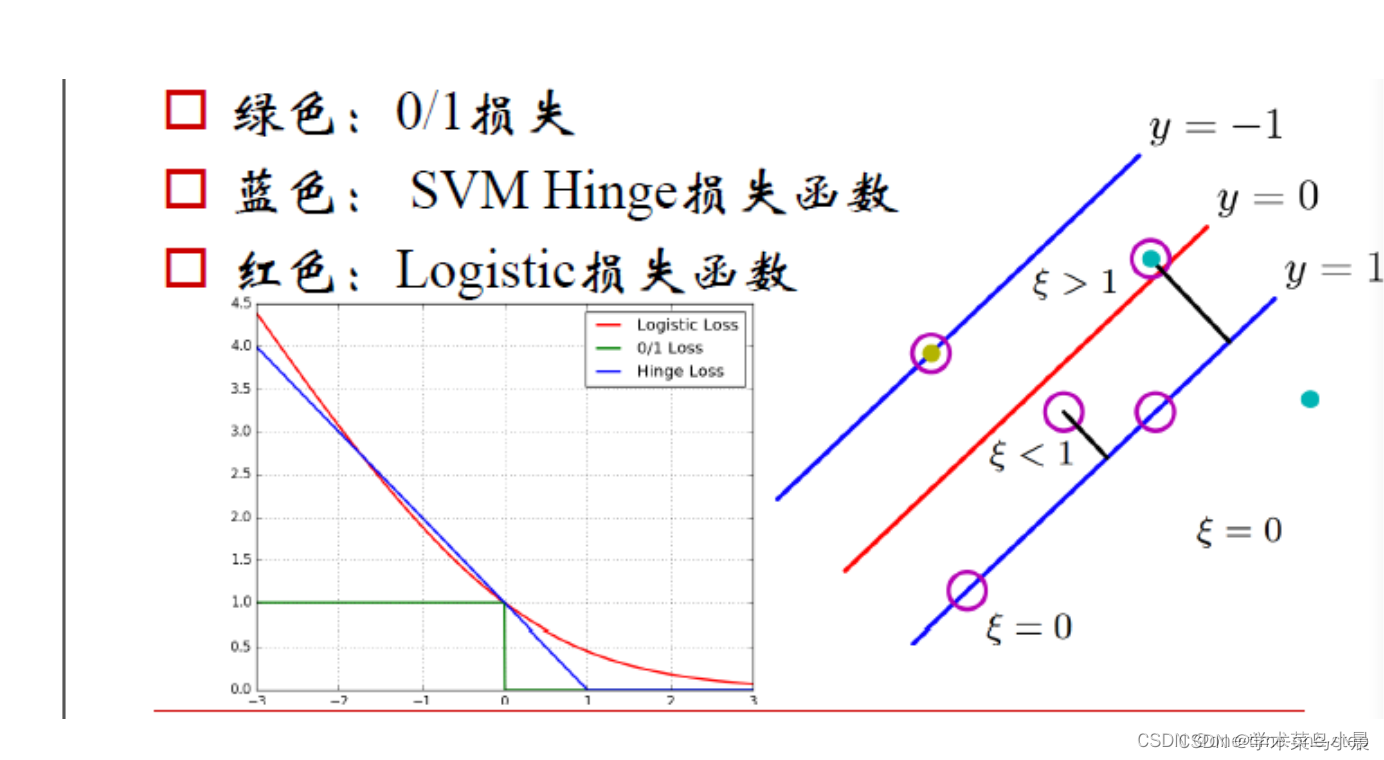
SVM 的三種損失函數衡量模型的性能。

? 1. 0-1 損失：
??????? 當正例樣本落在 y=0 下方則損失為 0，否則損失為 1.
??????? 當負例樣本落在 y=0 上方則損失為0，否則損失為 1.
?? 2.? Hinge （合頁）損失：
??????? 當正例落在 y >= 1 一側則損失為0，否則距離越遠則損失越大.
??????? 當負例落在 y <= -1 一側則損失為0，否則距離越遠則損失越大.
?? 3. Logistic 損失：
??????? 當正例落在 y > 0 一側，并且距離 y=0 越遠則損失越小.
??????? 當負例落在 y < 0 一側，并且距離 y=0 越遠則損失越小.

?

當存在線性不可分的場景時，我們需要使用核函數來提高訓練樣本的維度、或者將訓練樣本投向高維，SVM 默認使用 RBF 核函數，將低維空間樣本投射到高維空間，再尋找分割超平面。

• SVM的優點：

  • 在高維空間中非常高效；
  • 即使在數據維度比樣本數量大的情況下仍然有效；

• SVM的缺點：

  • 如果特征數量比樣本數量大得多，在選擇核函數時要避免過擬合；

  • 對缺失數據敏感;

  • 對于核函數的高維映射解釋力不強