1.DFS和BFS

1.1.DFS深度優先搜索

1.2.BFS廣度優先搜索

2.樹與圖的遍歷：拓撲排序

3.最短路

?3.1.迪杰斯特拉算法

3.2.貝爾曼算法

3.3.SPFA算法

3.4.多源匯最短路Floy算法

4.最小生成樹

4.1.普利姆算法

4.2.克魯斯卡爾算法

5.二分圖：染色法，匈牙利算法

5.1.染色法

5.2.匈牙利算法

1.DFS和BFS

1.1.DFS深度優先搜索

深度優先搜索（Depth-First Search, DFS）是一種用于遍歷或搜索樹或圖的算法。它從起點開始，沿著一個路徑一直到達最深的節點，然后回溯到之前的節點，繼續探索下一個路徑，直到所有的節點都被訪問過。

DFS使用一個棧來存儲待訪問的節點，它會將起點壓入棧中，然后重復執行以下步驟直到棧為空：

彈出棧頂節點。
如果該節點是目標節點，則搜索結束。
否則將該節點標記為已訪問，并將其所有未訪問的鄰居節點按照某種規則（如按字母表順序）依次壓入棧中。

使用DFS的優點是它的空間復雜度相對較小，因為它只需要存儲一條路徑上的節點。但是，如果搜索的圖或樹非常大，DFS可能會陷入死循環或者長時間運行。此外，DFS不一定能找到最優解，因為它只探索了一條路徑，而不是所有可能的路徑。

因此，在實際應用中，需要根據具體問題的要求選擇合適的搜索算法。例如，如果需要找到最短路徑，可能更適合使用廣度優先搜索（Breadth-First Search, BFS）算法。

842.排列數字：

給定一個整數n，將數字1~n排成一排，將會有很多排列方法。

現在，請你按照字典序將所有的排列方法輸出。

#include<iostream>
using namespace std;
?
const int N = 7;
?
int n;
int path[N];
bool st[N];
?
void dfs(int u)
{if(u == n){for(int i = 0;i < n; i++)printf("%d ", path[i]);printf("\n");return;}for(int i = 1;i <= n; i++){if(!st[i]){path[u] = i;st[i] = true;dfs(u+1);st[i] = false;}}
}
?
int main()
{scanf("%d", &n);dfs(0);return 0;
}

843.n-皇后問題：

n-皇后問題是指將n個皇后放在n-n的國際棋盤上，使得皇后不能相互攻擊到，即任意兩個皇后都不能處于同一行、同一列或同一斜線上。

現在給定整數n，請你輸出所有的滿足條件的棋盤擺法。

法1

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
const int N = 20;
?
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
?
void dfs(int u)
{if(u == n){for(int i = 0;i < n; i++)puts(g[i]);printf("\n");return;}fot(int i = 1;i <= n; i++){if(!col[i] && !dg[u + i] && !udg[n - u + i]){path[u] = i;col[i] = dg[u + i] = udg[n - u + i] = true;dfs(u+1);col[i] = dg[u + i] = udg[n - u + i] = false;g[u][i] = '·';}}
}
?
int main()
{scanf("%d", &n);for(int i = 0;i < n; i++){for(int j = 0;j < n; j++)g[i][j] = '·';}dfs(0);return 0;
}

法2：

#include<iostream>
using namespace std;
?
const int N = 20;
?
int n;
char g[N][N];
bool row[N], col[N], dg[N * 2], udg[N * 2];
?
void dfs(int x, int y, int s)
{if(y == n){y = 0;x++;}if(x == n){if(s == n){for(int i = 0;i < n; i++)puts(g[i]);puts("");}return;}//不放皇后dfs(x, y+1, s);//放皇后if(!row[x] && !col[y] && !dg[x+y] && !udg[x-y+n]){g[x][y] = 'Q';row[x] = col[y] = dg[x+y] = udg[x-y+n] = true;dfs(x, y+1, s+1);row[x] = col[y] = dg[x+y] = udg[x-y+n] = false;g[x][y] = '.';}
}
?
int main()
{scanf("%d", &n);for(int i = 0;i < n; i++){for(int j = 0;j < n; j++){g[i][j] = '.';}}dfs(0, 0, 0);return 0;
}

1.2.BFS廣度優先搜索

廣度優先搜索（Breadth-First Search, BFS）是一種用于遍歷或搜索樹或圖的算法。它從起點開始，首先訪問所有與起點直接相鄰的節點，然后訪問這些節點的相鄰節點，以此類推，直到所有的節點都被訪問過。

BFS使用一個隊列來存儲待訪問的節點，它會將起點壓入隊列中，然后重復執行以下步驟直到隊列為空：

彈出隊列首部節點。
如果該節點是目標節點，則搜索結束。
否則將該節點標記為已訪問，并將其所有未訪問的鄰居節點按照某種規則（如按字母表順序）依次壓入隊列中。

使用BFS的優點是它能夠保證在最少的時間內找到目標節點，因為它是按照距離從起點由近到遠進行搜索的。此外，BFS也能夠處理有向無環圖（DAG）和圖的情況。但是，如果搜索的圖或樹非常大，BFS可能需要較大的空間來存儲隊列中的節點，因此空間復雜度較大。

因此，在實際應用中，需要根據具體問題的要求選擇合適的搜索算法。例如，如果需要找到深度優先搜索的最短路徑，可能更適合使用深度優先搜索算法。

844.走迷宮：

給定一個n*m的二維整數數組，用來表示一個迷宮，數組中只包含0成1，其中0表示可以走的路，表示不可通過的墻壁。最初，有一個人位于左上角(1, 1)處，已知該人每次可以向上、下、左、右任意一個方向移動一個位置。

請問，該人從左上角移動至右下角(n, m)處，至少需要移動多少次。

數據保證(1, 1)處和(n, m)處的數字為0，且一定至少存在1條通路。

程序代碼1：

#include<iostream>
#include<queue>
#include<cstring>
?
using namespace std;
?
const int N = 110;
?
typedef pair<int, int> PII;
?
int g[N][N];
int d[N][N];
int n, m;
?
int bfs()
{queue<pair<int, int>> q;q.push({0, 0});memset(d, -1, sizeof(d));d[0][0] = 0;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};while(q.size()){PII t = q.front();q.pop();for(int i = 0;i < 4; i++){int x = t.first + dx[i], y = t.second + dy[i];if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1){d[x][y] = d[t.first][t.second] + 1;q.push({x, y});}}}return d[n-1][m-1];
}
?
int main()
{scanf("%d%d", &n, &m);for(int i = 0;i < n; i++)for(int j = 0;j < m; j++)scanf("%d", &g[i][j]);cout << bfs() << endl;return 0;
}

打印路徑代碼：

#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
?
typedef pair<int, int> PII;
const int N = 110;
?
int n, m;
int g[N][N];
int d[N][N];
int prev[N][N];
PII q[N * N];
?
int bfs()
{int hh = 0, tt = 0;q[0] = {0, 0};memset(d, -1, sizeof(d));d[0][0] = 0;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};while(hh <= tt){auto t = q[hh++];for(int i = 0;i < 4; i++){int x = t.first + dx[i], y = t.second + dy[i];if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == 0 && d[x][y] == -1){d[x][y] = d[t.first][t.second] + 1;prev[x][y] = t;q[++tt] = {x, y};}}}int x = n - 1, y = m - 1;while(x || y){cout << x << ' ' << y << endl;auto t = prev[x][y];x = t.first, y = t.second;}return d[n-1][m-1];
}
?
int main()
{scanf("%d%d", &n, &m);for(int i = 0;i < n; i++){for(int j = 0;j < m; j++){scanf("%d", g[i][j]);}}cout << bfs() << endl;return 0;
}

5 5

0 1 0 0 0

0 1 0 1 0

0 0 0 0 0

0 1 1 1 0

0 0 0 1 0

八數碼

樹是一種特殊的圖，屬于無環圖。

圖分為有向圖和無向圖。

846.樹的重心：

給定一棵樹，樹中包含n個結點（編號1~n）和n-1條無向邊。

請你找出樹的重心，并輸出將重心刪除后剩余各個連通塊中點數的最大值。

重心定義：重心是指樹中的一個節點，如果將這個結點刪除后，剩余各個連通塊中點數的最大值最小，那么這個節點被稱為樹的重心。

代碼：

#include<iostream>
using namespace std;
?
const int N = 100010, M = N * 2;
?
int n, m;
int h[N], e[M], ne[M], idx;
bool st[N];
int ans = N;
?
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
?
int dfs(int u)
{st[u] = true;//標記一下int sum = 0, res = 0;for(int i = h[u];i != -1; i = ne[i]){int j = e[i];if(!st[j]){int s = dfs(j);res = max(res, s);sum += s;}}res = max(res, n - sum - 1);ans = min(ans, res);return sum + 1;
}
?
int main()
{scanf("%d", &n);memset(h, -1, sizeof(h));for(int i = 0;i < n - 1; i++){int a, b;cin >> a >> b;add(a, b), add(b, a);}dfs(1);cout << ans << endl;return 0;
}

847.圖中點的層次：

給定一個n個點m條邊的有向圖，圖中可能存在重邊和自環。

所有邊的長度都是1，點的編號為1~n。

請你求出1號點到n點的最短距離，如果從1號點無法走到n號點，輸出-1。

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
const int N = 1e5 + 10;
?
int n, m;
int h[N], e[N], ne[N], idx;
int d[N], q[N];
?
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
?
int bfs()
{int hh = 0, tt = 0;q[0] = 1;memset(d, -1, sizeof(d));d[1] = 0;while(hh <= tt){int t = q[hh++];for(int i = h[t];i != -1; i = ne[i]){int j = e[i];if(d[j] == -1){d[j] = d[t] + 1;q[++tt] = j;}}}return d[n];
}
?
int main()
{cin >> n >> m;memset(h, -1, sizeof(h));for(int i = 0;i < m; i++){int a, b;cin >> a >> b;add(a, b);}cout << bfs() << endl;return 0;
}

2.樹與圖的遍歷：拓撲排序

848.有向圖的拓撲序列

給定一個n個點m條邊的有向圖，圖中可能存在重邊和自環。

請輸入任意一個該有向圖的拓撲序列，如果拓撲序列不存在，則輸出-1.

若一個由圖中所有點構成的序列A滿足：對于圖中的每一條邊(x, y)，x在A中都有出現在y之前，則稱A是該圖的一個拓撲序列。

有向無環圖——拓撲圖

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
const int N = 1e5 + 10;
?
int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N];
?
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
?
bool topsort()
{int hh = 0, tt = 0;for(int i = 1;i <= n; i++){if(!d[i])q[++tt] = i;}while(hh <= tt){int t = q[hh++];for(int i = h[t];i != -1; i = ne[i]){int j = e[t];d[j]--;if(d[j] == 0){q[++tt] = j;}}}return tt == n - 1;
}
?
int main()
{cin >> n >> m;memset(h, -1, sizeof(h));for(int i = 0;i < n; i++){int a, b;cin >> a >> b;add(a, b);d[b]++;}if(topsort()){for(int i = 0;i < n; i++)printf("%d ", q[i]);puts("");}elseputs("-1");cout << << endl;return 0;
}

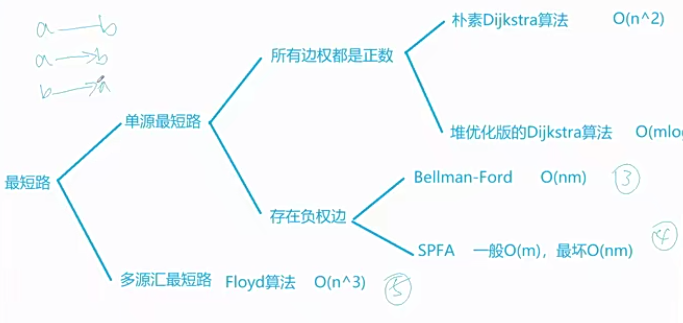
3.最短路

最短路問題是在給定的有向圖或無向圖中找到從起點到終點的最短路徑的問題。這個問題在計算機科學和應用數學中有著廣泛的應用，例如在路由算法、交通控制和電路設計中都需要解決最短路問題。

解決最短路問題的方法主要有兩種：Dijkstra算法和Bellman-Ford算法。

Dijkstra算法是一種貪心算法，它基于圖論的原理，通過不斷更新起點到各個節點的最短距離，最終求得起點到終點的最短路徑。該算法的基本思路是從起點開始，每次選擇一個距離起點最近的節點，并更新起點到各個節點的距離。通過不斷重復這個過程，最終可以得到起點到終點的最短路徑。

Bellman-Ford算法是一種動態規劃算法，它可以處理帶有負權邊的圖。該算法的基本思路是通過對所有節點進行多次松弛操作，逐步更新起點到各個節點的最短距離。在每次松弛操作中，該算法會檢查是否存在一個節點的距離可以通過其他節點的路徑得到更短的距離，如果有，則更新該節點的距離。通過多次松弛操作，該算法可以找到起點到終點的最短路徑。

除了這兩種算法，還有其他一些解決最短路問題的方法，例如Floyd-Warshall算法和A*算法等。不同的算法適用于不同類型的圖和不同的應用場景，需要根據具體情況選擇合適的算法。

uTools_1689583511271

?3.1.迪杰斯特拉算法

Dijkstra算法是一種用于解決最短路徑問題的算法，它可以在帶權重的圖中找到從一個起點到所有其他節點的最短路徑。

該算法的基本思路是從起點開始，每次選擇距離最短的節點作為中轉點，并將該節點的鄰居節點更新距離，直到所有節點都被訪問過或者沒有可達的節點。

具體實現過程如下：

初始化：將起點的距離設置為0，其他節點的距離設置為無窮大。
選擇中轉點：從起點開始，選擇距離起點最近的節點作為中轉點，將該節點的距離更新為起點到該節點的距離。
更新距離：對于中轉點周圍的鄰居節點，如果從起點到該鄰居節點的距離比之前的距離更短，則更新該鄰居節點的距離為起點到該鄰居節點的距離。
重復步驟2和步驟3，直到所有節點都被訪問過或者沒有可達的節點。
輸出結果：最終得到從起點到所有節點的最短路徑。

Dijkstra算法的時間復雜度為O(n^2)，其中n是節點的數量。如果使用堆優化可以將時間復雜度優化為O(m log n)，其中m是邊數。

849.Dijkstra求最短路I：

給定一個n個點m條邊的1有向圖，圖中可能存在重邊和自環，所以邊權均為正值。

請你求出1號點到n號點的最短距離，如果無法從1號點走到n號點，則輸出-1.

3 3

1 2 2

2 3 1

1 3 4

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
const int N = 510;
?
int n, m;
int g[N][N];
int dist[N][N];
bool st[N];
?
int dijkstra()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;for(int i = 0;i < n; i++){int t = -1;for(int j = 1;j <= n; j++)if(!st[j] && (t == -1 || dist[t] > dist[j]))t = j;st[t] = true;for(int j = 1;j <= n; j++)dist[j] = min(dist[j], dist[t] + g[t][j]); ? ?}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
?
int main()
{cin >> n >> m;memset(g, 0x3f, sizeof(g));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = min(g[a][b], c);}int t = dijkstra();printf("%d\n", t);return 0;
}

Dijkstra求最小短路II：

堆優化版dijkstra算法

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
typedef pair<int, int> PII;
?
const int N = 1e5 + 10;
?
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
?
void add(int a,int b,int c)
{e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx++;
}
?
int dijkstra()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, 1});while(heap.size()){auto t = heap.top();heap.pop();int ver = t.second, distance = t.first;if(st[ver]) continue;for(int i = h[ver];i != -1; i = ne[i]){int j = e[i];if(dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({dist[j], j});}}}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
?
int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof(h));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}int t = dijkstra();printf("%d\n", t);return 0;
}

3.2.貝爾曼算法

Bellman-Ford算法

for循環n次，每一次循環所有邊

dist[b] = min(dist[b], dist[a]) 松弛操作

dist[b] ≤ dist[a] + w三角不等式有負權邊就很難成立啦

853.有邊數限制的最短路：

給定一個n個點m條邊的有向圖，圖中可能存在重邊和自環，邊權可能為負數。

請你求出從1號點到n號點的最多經過k條邊的最短距離，如果無法從1號點走到n號點，輸出impossible。

注意：圖中可能存在負權回路。

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
const int N = 510, M = 10010;
?
int n, m, k;
iny dist[N], backup[N];
?
struct Edge
{int a, b, w;
}edges[M];
?
int bellman_ford()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;for(int i = 0;i < k; i++){memcpy(bakcup, dist, sizeof(backup));for(int j = 0;j < m; j++){int a = edges[j].a, b = edges[i].b, w = edges[i].w;dist[b] = min(dist[b], backup[a] + w);}}if(dist[n] > 0x3f3f3f3f / 2) return -1;return dist[n];
}
?
int main()
{scanf("%d%d%d", &n, &m, &k);for(int i = 0;i < m; i++){int a, b, w;scanf("%d%d%d", &a, &b, &w);edges[i] = {a, b, w};}int t = bellman_ford();if(t == -1)puts("impossible");else printf("%d\n", t);return 0;
}

3.3.SPFA算法

851.spfa求最短路

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
?
using namespace std;
?
typedef pair<int, int> PII;
?
const int N = 510, M = 10010;
?
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
?
void add(int a, int b, int c)
{e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx++;
}
?
int spfa()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;queue<int> q;q.push(1);st[1] = true;while(q.size()){int t = q.front();q.pop();st[t] = false;for(int i = h[t];i != -1; i = ne[i]){int j = e[i];if(dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];if(!st[j]){q.push(j);st[j] = true;}}}}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
?
int main()
{scanf("%d%d%d", &a, &b, &c);memset(h, -1, sizeof(h));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}int t = spfa();if(t == -1)puts("");elseprintf("%d\n", t);return 0;
}

852.spfa判斷負環：

給定一個n個點m條邊的有向圖，圖中可能存在重邊和自環，邊權可能為負數。

請你判斷圖中是否存在負權回路。

3 3

1 2 -1

2 3 4

3 1 -4

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
const int N = 10010;
?
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N], cnt[N];
bool st[N];
?
void add(int a, int b, int c)
{e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx++;
}
?
int spfa()
{queue<int> q;q.push(1);st[1] = true;while(q.size()){int t = q.front();q.pop();st[t] = false;for(int i = h[t];i != -1;i = ne[i]){int j = e[i];if(dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];cnt[j] = cnt[t] + 1;if(cnt[j] >= n) return true;if((!st[j])){q.push(j);st[j] = true;}}}}return false;
}
?
int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof(h));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}if(spaf())printf("Yes\n");elseprintf("No\n");return 0;
}

3.4.多源匯最短路Floy算法

for(int k = 1;k <= n; k++)
{for(i = 1;i <= n; i++){for(int j = 1;j <= n; j++){d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}
}

854.Floyd求最短路：

給定一個n個點m條邊的有向圖，圖中可能存在重邊和閉環，邊權可能為負數。

再給定k個詢問，每個詢問包含兩個整數x和y，表示查詢從點x到點y的最短距離，如果路徑不存在，則輸出“impossible”

數據保證圖中不存在負權回路。

#include<iostream>
#include<algorithm>
#include<cstring>
?
using namespace std;
?
const int N = 1e4 + 10;
?
int n, m, Q;
int d[N][N];
?
void floyd()
{for(int k = 1;k <= n; k++){for(int i = 1;i <= n; i++){for(int j = 1;j <= n; j++){d[i][j] = min(d[i][k], d[k][j]);}}}
}
?
int main()
{scanf("%d%d%d", &n, &m, &Q);for(int i = 1;i <= n; i++){for(int j = 1;j <= n; j++){if(i == j)d[i][j] = 0;elsed[i][j] = INF;}}while(m--){int a, b, w;scanf("%d%d%d", &a, &b, &w);d[a][b] = min(d[a][b], w);}floyd();while(Q--){int a, b;scanf("%d%d",&a, &b);if(d[a][b] == INF)puts("impossible");elseprintf("%d\n", d[a][b]);}return 0;
}

4.最小生成樹

最小生成樹的兩個算法：

普利姆算法（Prim）
克魯斯卡爾算法（Kruskal）

4.1.普利姆算法

樸素版Prim，類似于Dijkstra算法

Dijkstra算法的主體部分：

int dijkstra()
{memset(dist, -1, sizeof(dist));dist[1] = 0;for(int i = 0;i < n - 1; i++){int t = -1;for(int j = 1;j <= n; j++){if(!st[j] && (t == -1 || dist[t] > dist[j]))t = j;}for(int ?j = 1;j <= n; j++){dist[j] = min(dist[j], dist[t] + g[t][j]);}st[t] = true;}if(dist[n] == 0x3f3f3f3f)return -1;return dist[n];
}

prim的算法思路

dist[i] <- 正無窮

for(i = 0;i < n; i++)
{t->找到集合距離最近的點用t更新其他點到集合的距離，st[t] = true;
}

858.Prim算法求最小生成樹：

給定一個n個點m條邊的無向圖，圖中可能存在重邊和自環，邊權可能為負。

求最小生成樹的樹邊權重之和，如果最小生成樹不存在則輸出impossible。

給定一張邊帶權的無向圖G=(V, E)，其中V表示圖中點的集合，E表示圖中邊的集合，n=[V]，m=[E]

由V中的全部n個頂點和E中n-1條邊構成的無向連通子圖被稱為G的一棵生成樹，其中邊的權值之和和最小的生成樹被稱為無向圖G的最小連通圖。

4 5

1 2 1

1 3 2

1 4 3

2 3 2

3 4 4

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
cosnt int N = 1e4 + 10;
?
int n, m;
int g[N][N];
int dist[N];
bool st[N];
?
int prim()
{memset(dist, 0x3f, sizeof(dist));int res = 0;for(int i = 0;i < n; i++){int t = -1;for(int j = 1;j <= n; j++){if(!st[t] && (t == -1 || dist[t] > dist[j]))t = j;if(i && dist[t] == INF)return INF;if(i)res += dist[t];for(int j = 1;j <= n; j++)dist[j] = min(dist[j], g[t][j]);st[t] = true;}}return true;
}
?
int main()
{scanf("%d%d", &n, &m);memset(g, 0x3f, sizeof(g));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = g[b][a] = min(g[a][b], c);}int t = prim();if(t == INF)puts("impossible");elseprintf("%d\n", t);return 0;
}

堆優化版Prim

競賽中實際上用到的不多。

4.2.克魯斯卡爾算法

Kruskal算法的基本思想：

將所有邊按照權重從小到大排序
枚舉每條邊a，b，權重c 如果a，b不連通，就將這條邊加入到這個集合里面

859.Kruskal算法求最小生成樹：

4 5

1 2 1

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
const int N = 1e4 + 10;
?
int n, m;
int p[N];
?
struct Edge
{int a, b, w;bool operator< (const Edge &W)const{return w < W.w;}
}edges[N];
?
int find(int x)
{if(p[x] != x) p[x] = find(p[x]);return p[x];}
?
int main()
{scanf("%d%d", &n, &m);for(int i = 0;i < m; i++){int a, b, c;scanf("%d%d%d", &a, &b, &c);edges[i] = {a, b, w};}sort(edges, edges + m);for(int i = 1;i <= n; i++)p[i] = i;int res = 0, cnt = 0;for(int i = 0;i < m; i++){int a = edges[i].a, b = edges[i].b, w = edges[i].w;a = find(a), b = find(b);if(a != b){p[a] = b;res += w;cnt++;}}if(cnt < n - 1)puts("impossible");elseprintf("%d\n", res);return 0;
}

5.二分圖：染色法，匈牙利算法

二分圖當且僅當圖中不含奇數環。

二分圖又叫二部圖，是圖論中的一種特殊模型。設G=（V，E）是無向圖，如果根據頂點V可分割為兩個互不相交的子集（A，B），且圖中的每條邊（i，j）所關聯的兩個頂點i和j分屬這兩個不同的頂點集（i∈A，j∈B），則圖G就是一個二分圖。簡單來說，就是頂點集V可分割為兩個互不相交的子集，且圖中每條邊依附的兩個頂點都分屬于這兩個互不相交的子集，兩個子集內的頂點不相鄰。

二分圖有最大匹配和最小匹配問題，在二分圖中的一個匹配是指邊集中任意兩條邊都不依附于同一個頂點，極大匹配是指在當前已完成的匹配下，無法再通過增加未完成匹配的邊的方式來增加匹配的邊數，最大匹配是所有極大匹配當中邊數最大的一個匹配。

分辨是否是二分圖：

染色法 O(n + m)
匈牙利算法 O(mn)，實際運行時間一般遠小于O(mn)

5.1.染色法

二分圖染色法是一種判斷二分圖的方法，可以分為連通圖判斷和非連通圖判斷1。

染色思路如下：

初始所有頂點未染色。
隨意取出一個未染色的頂點u，把它染成一種顏色（假設為0）。
取與它連接的結點v，如果v未染色，則將v染成和u不同的顏色（假設為1），如果v已經染色，那么判斷u和v顏色是否相同，相同則表明染色失敗，該圖不是二分圖，結束。
遍歷所有結點，重復步驟）。
連通圖只需要一次dfs染色，非連通圖則多次dfs染色。

for(int i = 1;i <= n; i++)
{if(v未染色)dfs(i);
}

860.染色法判定二分圖

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
const int N = 1e5 + 10, M = 2e5 + 10;
?
int n, m;
int h[N], e[M], ne[M], idx;
int color[N];
?
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
?
bool dfs(int u, int father, int c)
{color[u] = c;for(int i = h[u];i != -1; i = ne[i]){int j = e[i];if(color[j] == -1){if(!dfs(j, 3 - c)) return false;}else if(color[j] == c) return false;}return true;
}
?
int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof(h));while(m--){int a, b;scanf("%d%d", &a, &b);add(a, b), add(b, a);}bool flag = true;for(int i = 1;i <= n; i++){if(!color[i]){if(!dfs(i, 1)){flag = false;break;}}}if(flag) puts("Yes");else puts("No");return 0;
}

題目：關押罪犯

5.2.匈牙利算法

匈牙利算法是一種在多項式時間內求解任務分配問題的組合優化算法，并推動了后來的原始對偶方法。

861.二分圖的最大匹配

給定一個二分圖，其中左半部包含n1個點（編號1~n1），右半部包含n2個點（編號1 ~n2），二分圖共包含m條邊。

數據保證任意一條邊的兩個端點都不可能在同一個部分。

請你求出二分圖的最大匹配數。

給定一個二分圖G，在G的一個子圖M中，M的邊集（E)的任意兩條邊都不依附于同一個頂點，則稱為一個匹配。

所有匹配中包含邊數最多的一組匹配稱為二分圖的最大匹配數。

#include<iostream>
#include<cstring>
#include<algorithm>
?
using namespace std;
?
const int N = 510, M = 1e5 + 10;
?
int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];
?
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
?
bool find(int x)
{for(int i = h[x];i != -1; i = ne[i]){int j = e[i];if(!st[j]){st[j] = true;if(match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}
?
int main()
{scanf("%d%d%d", &n1, &n2, &m);memset(h , -1, sizeof(h));while(m--){int a, b;scanf("%d%d", &a, &b);add(a, b);}int res = 0;for(int i = 1; i <= n1; i++){memset(st, false, sizeof(st));if(find(i)) res++;}printf("%d\n", res);return 0;
}

2 2 4

1 1

1 2

2 1

2 2