LeetCode Top100 Liked 題單（序號34~51）

?34. Find First and Last Position of Element in Sorted Array ?

題意：找到非遞減序列中目標的開頭和結尾

我的思路

用二分法把每一個數字都找到，最后返回首尾兩個數

代碼?Runtime12 ms Beats 33.23% Memory14 MB Beats 5.16%

class Solution {
public:void bins(int l,int r,int tar,vector<int>& nums,vector<int>& ans){while(l<=r){int mid=l+(r-l)/2;if(nums[mid]>tar) r=mid-1;else if(nums[mid]<tar)l=mid+1;else{ans.push_back(mid);bins(l,mid-1,tar,nums,ans);bins(mid+1,r,tar,nums,ans);return ;}}}vector<int> searchRange(vector<int>& nums, int target) {int n=nums.size();vector<int> ans;bins(0,n-1,target,nums,ans);if (ans.empty())return {-1,-1};else  sort(ans.begin(),ans.end());return {ans[0],ans[ans.size()-1]};}
};

標答

可以直接找到序列的頭部數字，和數字加一的序列的頭部數字

代碼?Runtime 3 ms Beats 96.59% Memory13.7 MB Beats 11.32%

class Solution {
public:pair<int,int> bins(vector<int>& nums,int tar,int l,int r){int ans=-1;while(l<=r){int mid=(l+r)/2;if(tar>nums[mid]) l=mid+1;else if(tar<nums[mid]) r=mid-1;else{//如果等于的話ans=mid;r=mid-1;}}if(ans==-1)return {l,0};return {ans,1};}vector<int> searchRange(vector<int>& nums, int target) {int n=(int)nums.size()-1;pair<int,int> st;   pair<int,int> en;st =bins(nums,target,0,n);en =bins(nums,target+1,0,n);if(!st.second) return {-1,-1};return {st.first,en.first-1};}
};

35.?Search Insert Position

題意：給定一個有序數組和一個元素，找到給序號，沒找到返回他應該插在哪里

我的思路

二分查找，我記得二分查找應該是有upper_bound和lower_bound直接用的

注意：lower_bound函數是返回指針，用于在指定區域內查找不小于目標值的第一個元素，也就是說[1,2,3,5]數組中，target為4的情況下返回的是序號為3；[1,2,3,4]數組中，target為4的情況下返回的是序號為3

upper_bound為大于目標元素的第一個數/位置，[1,2,3,5]數組中，target為4的情況下返回的是序號為3；[1,2,3,4]數組中，target為4的情況下返回的是序號為4

代碼?3ms Beats 88.42% 9.63mb Beats 47.66%

class Solution {
public:int searchInsert(vector<int>& nums, int target) {return lower_bound(nums.begin(), nums.end(), target) - nums.begin();}
};

39.?Combination Sum

題意：給定一個不同整數數組和一個目標，返回一個單獨的集合，使得集合內部和等于target；同一個數字可以用多次；

我的思路

好像是動態規劃做的？和背包問題差不多，但是我忘記了orz

標答 動態規劃

首先創建一個dp的vector，每個dp的內容是答案的格式，也就是vector<vector<int>>，dp表示的是從第一個數開始到target的每個數為target時的答案

狀態轉移方程為 dp[j]=dp[j-i]+i (這里的+時集合加入的意思)

代碼?Runtime 18 ms Beats 34.7% Memory14.3 MB Beats 40.40%

class Solution {
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector <vector <vector<int>>> dp(target+1);//首先要開辟空間，不然會runtime errordp[0]={{}}; //初始化for(int &i:candidates){//對于每一個在候選名單里的for(int j=i;j<=target;j++){//對于每個在數組里的ifor(auto v:dp[j-i]){//v是每一個答案中的集合v.push_back(i);dp[j].push_back(v);//要把更新的集合放回dp[j]中}}}return dp[target];}
};

標答 遞歸

遞歸的方法好像速度更快，首先將數組排序，之后遞歸，遞歸的引入參數為num；next是nums的索引，也就是遍歷了nums的每一個數字；psol是每一個集合，表示拿或者不拿的可能性；target是目標；result是最后的答案

注意：在一開始要排序，這么做是為了剪枝操作

因為 if(target<0)return; 這一操作同樣可以退出遞歸，但是如果target-candidates[next]<0 的時候推出遞歸，那么可以剪枝，大大提升速度；如果要達成這target-candidates[next]<0退出的操作，那么就必須要nums排序，這一才能加快速度

注意：psol傳入時要引用，不然會拖慢時間

代碼 Runtime2 ms Beats 91.39% Memory10.7 MB Beats 84.74%

class Solution {
public:void search(vector<int>& candidates, int next, int target, vector<int>& pol, vector<vector<int>> &result){if(target==0){//說明結束了result.push_back(pol);return;}if(next==candidates.size()||target-candidates[next]<0) return;pol.push_back(candidates[next]);//這是拿了,注意拿了還可以接著拿search(candidates,next,target-candidates[next],pol,result);pol.pop_back();search(candidates,next+1,target,pol,result);//這是沒拿，沒拿就走了}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());vector<int> pol;vector<vector<int>> result;//初始化search(candidates,0,target,pol,result);return result;}
};

41. First Missing Positive?

題意：給出未排序的nums，返回未在這些數字中的正整數

我的思路

好像博弈論中有這個算法，還涉及位運算？但是忘記了【好吧，答案中沒有位運算】

num的長度只有1e5，所以只能寫一個O n的算法了

代碼?Runtime 38 ms Beats 98.63% Memory41.3 MB Beats 34.99%

class Solution {
public:int firstMissingPositive(vector<int>& nums) {bool vis[100005]={0};int n=nums.size();for(int i=0;i<n;i++){if(nums[i]>100000||nums[i]<=0)continue;vis[nums[i]]=1;}for(int i=1;i<=100001;i++){if(vis[i]==0)return i;}return 0;}
};

另一道題 涉及位運算

給定一個包含 0, 1, 2, ..., n 中 n 個數的序列，找出 0 .. n 中沒有出現在序列中的那個數。

輸入: [3,0,1]
輸出: 2

輸入: [9,6,4,2,3,5,7,0,1]
輸出: 8

運用位運算來完成，思路為temp ^ nums[ i ] ^ (i + 1),這里的temp值從0開始，因為nums 的值是從0開始，而（i + 1）則是為了取到自然數1,2,3,4,5...等。運算規則如下：假如目標數組nums 值 為 0，1，2，4 自然數對應為1,2,3,4

0 ^ 1 ^ 0 = 1

1 ^ 2 ^ 1 = 2

2 ^ 3 ^ 2 = 3

3 ^ 4 ^ 4 = 3

返回值為3 缺失的數字即為3

class Solution {
public:int firstMissingPositive(vector<int>& nums) {int temp = 0;for(int i = 0;i < nums.size();i++){temp = temp ^ (i + 1) ^ (nums[i]);}return temp;}
};


42. Trapping Rain Water

題意：給一組正整數數組，表示寬度為1的磚塊的高度，問能存多少水

我的思路

費案1

單調棧，同時要記錄下每個磚塊的距離，所以棧里面存的是序號，一層一層的掃描？首先是y等于1之間的磚塊，之后是y=2之間的磚塊

假設是9?6 2?0 3?0 2 5 ，就是先9和6和3和0放入棧中；【如果一開始是0，就不放進去了】

height【i】=3來了把0彈出來，那么就直接彈出，之后棧頂是2，在計算0的那一個步驟，ans加上min(目前棧頂=2，height【i】=3)的數值，ans+=2；

目前棧頂是2，發現小于等于height【i】=3，那么就直接彈出，之后棧頂是6，在計算2的那一個步驟，ans+=id的差=2 * (height【i】=3 - 上一個彈出的數=2)的數值，ans+=2；當前棧為9 6 3

height【i】=0，不彈出；

height【i】=2，把0彈出來，直接彈出，之后棧頂是3，在計算0的那一個步驟，ans+=id的差=1?* (height【i】=2?- 上一個彈出的數=0)，ans+=2，目前棧為9 6 3 2

height【i】=5，目前棧頂是2，發現小于等于height【i】=5，直接彈出，之后棧頂是3，在計算0的那一個步驟所以ans=ans+（i=7? - top的序號=6-1 ）*（height【i】 -?上一個彈出的值=2），ans+=0，當前棧為9 6 3? ? ?ans不對

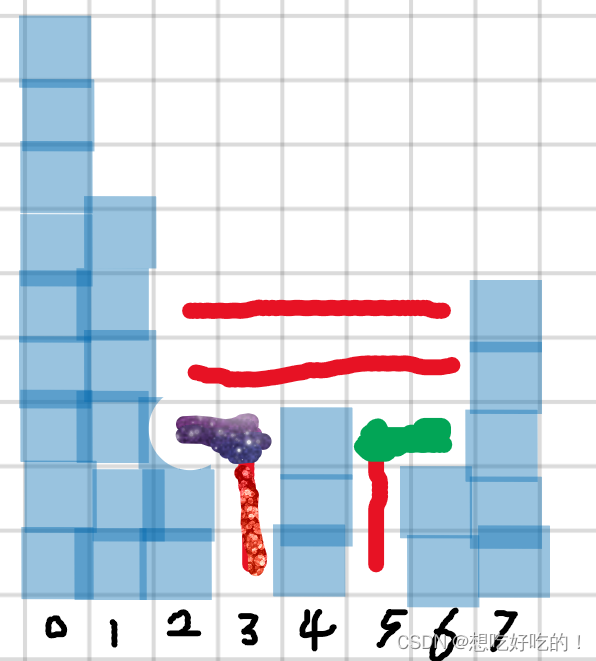
費案2

用減法，先減去磚塊占用水的體積

例如1 0?2?0 3?0 2 5 ，從右向左，mx=5，掃完一遍了，假設-1的位置有無限高的墻，

所以ans=【7-（-1）-1】*5-所有磚塊的體積，不對

標答 雙指針法 豎著加的

和上面的減法的思路差不多，但他是一個個豎著加起來

lmax代表最左邊的墻，rmax代表最右邊的墻前兩個if表示的是目前的lmax和rmax都不是最高的，應該要更新；第三個條件如果rmax大于lmax，ans加上lmax-h[lpos]；第四個條件如果lmax大于rmax，ans加上rmax-h[rpos]；為什么那么做？因為如果整個盆子左邊高于右邊，那么右側的水肯定能裝住，如果整個盆子右邊高于左邊，那么左側的水肯定能裝住。

代碼?Runtime6 ms Beats 97.75% Memory19.8 MB Beats 53.37%

注意?lpos<=rpos的等號

class Solution {
public:int trap(vector<int>& h) {int n=h.size()-1;int lmax=h[0],rmax=h[n];int lpos=1,rpos=n-1,ans=0;while(lpos<=rpos){        //等號if(rmax<=h[rpos]){rmax=h[rpos];rpos--;}else if(lmax<=h[lpos]){lmax=h[lpos];lpos++;}else if(rmax>=lmax){ans+=(lmax-h[lpos]);lpos++;}else{ans+=(rmax-h[rpos]);rpos--;}}return ans;}
};

標答 前綴和 豎著加的

dp[i]表示從左到右，以左邊的邊作為最高的邊，每個橫坐標 i 能裝多少水；之后從右到左，以右邊的邊作為最高的邊，res在每個橫坐標 i 上加上min ( 當前的最高 - dp[i] )

代碼 Runtime 12 ms Beats 78.67% Memory19.8 MB Beats 53.37%

class Solution {
public:int trap(vector<int>& h) {int n=h.size(),dp[20004]={0};int curmax=-1,ans=0;for(int i=0;i<n;i++){curmax=max(curmax,h[i]);dp[i]=curmax-h[i];}curmax=-1;for(int i=n-1;i>=0;i--){curmax=max(curmax,h[i]);ans+=min(dp[i],curmax-h[i]);}return ans;}
};

標答 單調棧 橫著加的

和費案1的思路相仿。棧中的數字越來越小，如果來了一個大的數，把這個數彈出，設cur是這個彈出的數，diff的序號的差，ans+=（min(當前棧頂的數，height[i] )?- 上一個彈出的數）*序號的差

為什么想費案1的時候沒有想出來呢？

height【i】=5，目前棧頂是2，發現小于等于height【i】=5，直接彈出，之后棧頂是3，在計算0的那一個步驟所以ans=ans+（i=7? - top的序號=6-1 ）*（height【i】 -?上一個彈出的值=2），ans+=0，當前棧為9 6 3?

因為從最上面的圖中可以看出，之前的步驟都是ans+=（min(當前棧頂的數，height[i] )?- 上一個彈出的數），但是當h[i]=5時，ans+=（當前棧頂的數 上一個彈出的數），沒有辦法把公式統一起來，所以沒做出來，明明只要加上取最小就可以了

為什么是取最小呢？

原理和標答1的原理是差不多的，因為答案是和兩側最小的那一條有關

補充：

1. 費案1中的棧根本不需要pair結構，因為有序號有數組就知道了數值了

2.?if(st.empty())break;這條語句是指左邊沒有邊可以作為盤子的左邊了，裝不下水了，所以break了

代碼?Runtime 12 ms Beats 78.67% Memory19.8 MB Beats 53.37%

class Solution {
public:int trap(vector<int>& h) {stack<int> st;int n=h.size(),ans=0;for(int i=0;i<n;i++){while(!st.empty()&&h[st.top()]<h[i]){//彈出操作int temp=st.top();st.pop();if(st.empty())break;//注意這句話int cha=i-st.top()-1;//注意這里是-1！！！！！！！ans+=(min(h[i],h[st.top()])-h[temp])*cha;}st.push(i);}return ans;}
};

45.?Jump Game II

題意：有n個序號從0開始的數組，你可以從num[i]，向右跳到【num[i]，num[i+j]】之間

我的思路

動態規劃，dp表示需要最少的次數，一開始初始化為無窮，dp[n-1]=0，最外層循環是i從n-1到0，第二層循環是j從1到num[i]，找到循環中最小的dp[i+j]，dp[i]=min( dp[ i + j ] + 1 )，返回答案dp[0]

但不幸的是n是1e4，nums是1e3，時間復雜度1e7

代碼?Runtime128 ms Beats 39.88% Memory16.8 MB Beats 41.3%

class Solution {
public:int jump(vector<int>& nums) {int n=nums.size();int dp[10004];for(int i=0;i<n;i++)dp[i]=9999;dp[n-1]=0;for(int i=n-2;i>=0;i--){int minn=9999;for(int j=1;j<=nums[i] && i+j<n;j++) minn=min(minn,dp[i+j]);dp[i]=minn+1;}return dp[0];}
};

要優化的話肯定是優化第二個循環，快速找到某個范圍內的最小值，想到樹狀數組，去看了看樹狀數組的板子，找到的樹狀數組代碼維護的是【1，i】范圍的最小值，網上說只有樹狀數組套樹狀數組或者線段樹才可以達到動態維護區間最小值

但是線段樹要從1開始建立，同時修改的時候不是單純的增減，而是直接替換，所以線段樹也不適合

標答 貪心

為什么可以用貪心算法呢？

乍一看想到動態規劃去了，才發現忽略了最大步長的信息（沒有的話就是DP了），因此不需要考慮跳多了的情況，而且題面能夠保證絕對能到達，所以不用擔心0步長的情形（跳不出去啦！）。

因此本題可以直接使用貪心算法：向后遍歷，找出能夠跳的最遠的選擇。

貪心最麻煩的地方就是全局最優解的證明，我這里給出一個簡單的思路：從同一個起點出發，如果當前選擇不是貪心選擇的，那么下一個選擇必然比貪心方案跳的更近。完成一次跳躍后有兩種情形：貪心方案的第二次選擇的位置是否存在于當前方案的第二次選擇中。存在，則最多選擇這個方案，此時當前方案會比貪心方案段（第二次選擇一樣，但是第一次選擇短了）；不存在，那么肯定是會短的（兩次選擇都短）。


參考鏈接：https://blog.csdn.net/cary_leo/article/details/115451900

簡單來說就是比誰跳的遠

代碼?Runtime 8 ms Beats 95.22% Memory16.6 MB Beats 64.1%

class Solution {
public:int jump(vector<int>& nums) {int n=nums.size(),ans=0;for(int i=1;i<n;i++){//要么選擇在這一格跳走，要么就留在這里nums[i]=max(nums[i-1],nums[i]+i);//nums代表在i位置可以到達的最遠的位置}int st=0;while(st<n-1){ans++; st=nums[st];}return ans;}
};


46.?Permutations

題意：有一個數組，里面的數字各不相同，返回所有排列

我的思路

用dfs做，沒寫出來；我好像還記得C++庫中有個直接全排列的調用

標答 dfs 回溯法

照著我寫壞的和表達對照一下，我用了兩次dfs，一次是沒取走數字，一次是取走了數字；不需要沒取走數字的那一組，因為他會因為個數不夠而不能加入最終答案的vector，所以只要取走的那一次dfs就可以了

代碼?Runtime 6 ms Beats 18.86% Memory8.2 MB Beats 11.7%

class Solution {
public:void dfs(vector<int>& nums,vector<int>& pol,vector<vector<int>>& ans,vector<int> vis){if(pol.size()==nums.size()){ans.push_back(pol);return;}for(int i=0;i<nums.size();i++){if(vis[i]) continue;vis[i]=1;pol.push_back(nums[i]);dfs(nums,pol,ans,vis);pol.pop_back();vis[i]=0;}}vector<vector<int>> permute(vector<int>& nums) {vector<int> pol; vector<vector<int>> ans; vector<int> vis((int)nums.size(),0);dfs(nums,pol,ans,vis);return ans;}
};

標答 dfs 交換

確實，不斷交換就可以排序完成了，還不會有多余的沒到個數的pol（和上一個做法不同）

代碼 Runtime 5 ms Beats 29.21% Memory 7.5 MB Beats 81.96%

class Solution {
public:vector<vector<int>> result;void permutation(vector<int> &nums,int i,int n){if(i==n){result.push_back(nums);return ;}for(int j=i;j<=n;j++){swap( nums[i],nums[j]);permutation(nums,i+1,n);//注意這里是i+1swap( nums[i],nums[j]);}}vector<vector<int>> permute(vector<int>& nums) {permutation(nums,0,nums.size()-1);return result;}
};

48. Rotate Image?

題意：將整個矩陣順時針旋轉90度，注意不要新開一個矩陣

我的思路

按照這個順序，一個圈層只要3組交換就可以了，實際操作的時候注意 i 和 j 的范圍！！！！！

例子1：初始

1 2 3

4 5 6

7 8 9

第一次

7 2 3

8 5 6

9 4 1

第二次

7 2 1

8 5 4

9 6 3

第三次

7 4 1

8 5 2

9 6 3

例子2：初始

4 8

3 6

第一次

3 8

6 4

第二次

3 4

6 8

第三次

循環直接結束了

代碼?Runtime 0 ms Beats 100% Memory 7.2 MB Beats 14.63%

class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n=matrix.size();for(int i=0;i<n/2;i++){//圈層for(int j=i;j<n-i;j++){swap(matrix[j][i],matrix[n-1-i][j]);}for(int j=i+1;j<n-i;j++){swap(matrix[n-1-i][j],matrix[n-1-j][n-1-i]);}for(int j=i+1;j<n-1-i;j++){swap(matrix[i][j],matrix[j][n-1-i]);}}}
};

標答 思維

先對角反轉，之后逆向

例子1：初始

1 2 3

4 5 6

7 8 9

第一次

1 4 7

2 5 8

3 6 9

第二次

7 4 1

8 5 2

9 6 3

代碼?Runtime 0 ms Beats 100% Memory7.3 MB Beats14.63%

class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();int m = matrix[0].size();vector<vector<int>> temp(n, vector<int>(m, 0));for(int i=0; i<n; i++){for(int j=0; j<i; j++){swap(matrix[i][j], matrix[j][i]);}}for(int i=0; i<n; i++){reverse(matrix[i].begin(), matrix[i].end());}}
};


49.?Group Anagrams

題意：給一組字符串，把字母相同的字符串放在一組里

我的思路

只能想到死做，就是map映射，key是字典序排列，value是vector<string>，之后遍歷map，組成答案

代碼?Runtime 30 ms Beats83.8%?Memory20.8 MB Beats 30.73%

class Solution {
public:vector<vector<string>> groupAnagrams(vector<string>& strs) {map<string,vector<string> > mp;int n=strs.size();for(int i=0;i<n;i++){string tmp=strs[i];sort(tmp.begin(),tmp.end());mp[tmp].push_back(strs[i]);}vector< vector<string> > ans;for(auto q:mp)ans.push_back(q.second);return ans;}
};

優化

看了標答，確實是這樣做的，但是sort和map和遍歷可以優化，map改成unorder_map，for(auto q:mp)加上引用【這一步突然時間少一半】

代碼?Runtime 15 ms Beats 99.87% Memory19.5 MB Beats 84.31%

class Solution {
public:vector<vector<string>> groupAnagrams(vector<string>& strs) {unordered_map<string,vector<string> > mp;int n=strs.size();for(int i=0;i<n;i++){string tmp=strs[i];sort(tmp.begin(),tmp.end());mp[tmp].push_back(strs[i]);}vector< vector<string> > ans;for(auto &q:mp)ans.push_back(q.second);return ans;}
};

51.?N-Queens

題意：皇后攻擊的范圍是所屬的橫線、豎線、斜線，在n*n的棋盤上擺放皇后，使得n個皇后不會互相攻擊

我的思路

遞歸

代碼?Runtime4 ms Beats 78.35% Memory7.8 MB Beats 36.39%

class Solution {
public:bool check(int n,int id, int j, vector<int>&pol){for(int i=0;i<pol.size();i++)if(pol[i]==j) return 0;for(int i=0;i<pol.size();i++){if(pol[i]-i ==j-id)return 0;}for(int i=0;i<pol.size();i++){if(pol[i]+i ==j+id)return 0;}return 1;}void se(int n,int id, vector<int>&pol, vector<vector<string>> & result) {if(pol.size()==n){vector<string> mp;for(int j=0;j<n;j++){//列string s (n, '.');s[pol[j]]='Q';mp.push_back(s);}result.push_back(mp);return;}for(int j=0;j<n;j++){//列if(!check(n,id,j,pol))//判斷這一列上有無其他數字，判斷斜線上有無其他數字;如果不可以放在這里，就跳過continue;pol.push_back(j);se(n,id+1,pol,result);pol.pop_back();}}vector<vector<string>> solveNQueens(int n) {vector<int> pol; vector<vector<string>> result;//假設返回的vector<int>表示每一行的皇后放在第n列se(n,0,pol,result);//id代表在第幾行return result;}
};

優化 位運算 沒看懂

10394 用位運算速解 n 皇后問題 - 知乎 (zhihu.com)

class Solution {
public:vector <vector <string>> ans;void solve(int n, int row, int colMask, int leftDiagMask, int rightDiagMask, vector <string> &board) {if (row == n) {ans.push_back(board);return;}int rowState = (colMask | leftDiagMask | rightDiagMask) & ((1 << n) - 1);int safePos = rowState ^ ((1 << n) - 1);while (safePos) {int queenPos = safePos & (-safePos);safePos -= queenPos;if (!(queenPos & rowState)) {board[row][log2(queenPos)] = 'Q';solve(n, row + 1, colMask | queenPos, (leftDiagMask | queenPos) << 1, (rightDiagMask | queenPos) >> 1, board);board[row][log2(queenPos)] = '.';}}}vector<vector<string>> solveNQueens(int n) {vector <string> board(n, string (n, '.'));solve(n, 0, 0, 0, 0, board);return ans;}
};

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/40313.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/40313.shtml
英文地址，請注明出處：http://en.pswp.cn/news/40313.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

前端練手小項目--自定義時間（html+css+js）

前端練手小項目--自定義時間（html+css+js）

自定義時間 寫文章的因 關于要寫這篇文章的原因 是記錄在工作上遇到的困難需求&#xff0c;是希望能給大家提供一些解決問題的思路 接下來我描述這個需求的多樣性&#xff0c;難點在哪。 勾選勾選框開始時間與結束時間默認顯示昨天與今天。取消勾選框開始時間與結束時間清空。…
閱讀更多...
如何查看線程在哪個cpu核上

如何查看線程在哪個cpu核上

1、ps -eLF查看PSR值 2、 taskset -pc $pid&#xff08;進程/線程&#xff09; 參考鏈接&#xff1a;https://blog.csdn.net/test1280/article/details/87993669
閱讀更多...
Ubuntu修改設置系列--修改ssh端口號的方法(有示例)

Ubuntu修改設置系列--修改ssh端口號的方法(有示例)

原文網址&#xff1a;Ubuntu修改設置系列--修改ssh端口號的方法(有示例)_IT利刃出鞘的博客-CSDN博客 簡介 說明 本文介紹Ubuntu修改ssh端口號的方法(有示例)。 要達成的目標 ssh添加一個端口&#xff1a;3333&#xff0c;關閉原來的22端口。 1.修改端口 修改配置文件/et…
閱讀更多...
thingsboard編譯安裝踩坑記錄

thingsboard編譯安裝踩坑記錄

thingsboard編譯安裝踩坑記錄 一、編譯&#xff1a;二、運行 朋友的thingsboard沒人維護&#xff0c;要裝新的服務器&#xff0c;啥文檔也沒有&#xff0c;就讓參考官網的文檔&#xff0c;版本也比較老3.2.2的&#xff0c;拿過來試了試記錄下踩坑的地方。 一、編譯&#xff1a;…
閱讀更多...
get與post如何拼接url與數據的靈活處理，循環的重要性。

get與post如何拼接url與數據的靈活處理，循環的重要性。

get與post拼接url地址不同&#xff1a; let postData {method: "post",data: {op: "/api/setting/maintenanceperiod?period"this.authorizationCode,loadingConfig: {},data: {period:this.authorizationCode}}}; if(this.editData.id){let postData …
閱讀更多...
Nginx運行Vue項目：基本運行

Nginx運行Vue項目：基本運行

需求 在Nginx服務器中&#xff0c;運行Vue項目。 說明 Vue項目打包生成的生產文件&#xff0c;是無法直接在瀏覽器打開的。需要放到Nginx服務器中&#xff0c;才能夠訪問。 本文章只介紹最基本的情況&#xff1a;Nginx中運行一個Vue項目。 實際生產環境&#xff0c;一個Ng…
閱讀更多...
mysql 批量給數據表和字段添加注釋

mysql 批量給數據表和字段添加注釋

1、用命令行導出 mysql數據庫中的所有表 首先查看 mysql 的配置文件 “/etc/my.cnf ”&#xff0c;配置中找到 datadir 目錄&#xff0c; 將文件導出到 datadir 目錄下 我的 datadir 目錄是&#xff1a; /var/lib/mysql 連接mysql&#xff0c;執行導出命令 SELECT TABLE_NAM…
閱讀更多...
解密 AI 客服；在不同硬件設備上運行大型語言模型的可能性

解密 AI 客服；在不同硬件設備上運行大型語言模型的可能性

&#x1f989; AI新聞 &#x1f680; 微軟必應首席執行官稱必應聊天優于OpenAI的GPT-4&#xff0c;但成本更高 摘要&#xff1a;微軟必應的首席執行官米哈伊爾?帕拉欣表示&#xff0c;必應聊天表現優于OpenAI的GPT-4&#xff0c;但使用了更高成本的檢索增強推理技術。必應聊…
閱讀更多...
中科億海微ROM使用

中科億海微ROM使用

標題 ROM&#xff08;Read-Only Memory&#xff0c;只讀存儲器&#xff09;是一種在FPGA&#xff08;Field-Programmable Gate Array&#xff0c;現場可編程門陣列&#xff09;中常用的存儲器類型。與RAM&#xff08;Random Access Memory&#xff0c;機存取存儲器&#xff09;…
閱讀更多...
Nginx安全加固，版本隱藏及HTTP請求頭修改方法

Nginx安全加固，版本隱藏及HTTP請求頭修改方法

1 隱藏nginx版本號 1.1 引言 nginx作為目前較為流行的http server軟件&#xff0c;其相關的安全漏洞也非常多&#xff0c;攻擊者可以根據我們的nginx版本來了解到相關的漏洞從而針對性的進行攻擊。 通過新版本的nginx都會修復一些老版本的已知漏洞&#xff0c;但有時候我們生…
閱讀更多...
二刷LeetCode--148. 排序鏈表(C++版本),必會題，思維題

二刷LeetCode--148. 排序鏈表(C++版本),必會題，思維題

思路&#xff0c;本題其實考察了兩個點&#xff1a;合并鏈表、鏈表切分。首先從1開始&#xff0c;將鏈表切成一段一段&#xff0c;因為需要使用歸并&#xff0c;所以下一次的切分長度應該是當前切分長度的二倍&#xff0c;每次切分&#xff0c;我們拿出兩段&#xff0c;然后將第…
閱讀更多...
虛擬機與Java虛擬機介紹

虛擬機與Java虛擬機介紹

1、虛擬機 所謂虛擬機&#xff08;Virtual Machine&#xff09;&#xff0c;就是一臺虛擬的計算機。它是一款軟件&#xff0c;用來執行一系列虛擬計算機指令。大體上&#xff0c;虛擬機可以分為系統虛擬機和程序虛擬機。大名鼎鼎的Visual Box&#xff0c;VMware就屬于 系統虛…
閱讀更多...
提示丟失vcomp140.dll怎么辦？如何快速修復vcomp140.dll丟失問題

提示丟失vcomp140.dll怎么辦？如何快速修復vcomp140.dll丟失問題

最近我遇到了一個程序啟動失敗的問題&#xff0c;錯誤提示顯示缺少了vcomp140.dll文件。經過一番研究和嘗試&#xff0c;我終于成功修復了這個問題。在這里&#xff0c;我將分享一下我的修復方法。 目錄 vcomp140.dll是什么&#xff1f; 如何快速修復呢&#xff1f; vcomp140…
閱讀更多...
sCrypt編程馬拉松于8月13日在復旦大學成功舉辦

sCrypt編程馬拉松于8月13日在復旦大學成功舉辦

繼6月在英國Exeter大學成功舉辦了為期一周的區塊鏈編程馬拉松后&#xff0c;美國sCrypt公司創始人兼CEO劉曉暉博士帶領核心團隊成員王一強、鄭宏鋒、周全&#xff0c;于8月13日在復旦大學再次成功舉辦了一場全新的sCrypt編程馬拉松。 本次活動由上海可一澈科技有限公司與復旦大…
閱讀更多...
C++筆記之花括號和圓括號初始化區別，列表初始化和初始化列表區別

C++筆記之花括號和圓括號初始化區別，列表初始化和初始化列表區別

C筆記之花括號和圓括號初始化區別&#xff0c;列表初始化和初始化列表區別 code review! 文章目錄 C筆記之花括號和圓括號初始化區別&#xff0c;列表初始化和初始化列表區別1.花括號{}進行初始化和圓括號()進行初始化2.列表初始化&#xff08;list initialization&#xff0…
閱讀更多...
Vitis高層次綜合學習——FPGA

Vitis高層次綜合學習——FPGA

高層次綜合 什么是高層次綜合&#xff1f;就是使用高級語言&#xff08;如C/C&#xff09;來編寫FPGA算法程序。 在高層次綜合上并不需要制定微架構決策&#xff0c;如創建狀態機、數據路徑、寄存器流水線等。這些細節可以留給 HLS 工具&#xff0c;通過提供輸入約束&#xff…
閱讀更多...
專訪阿里云席明賢，視頻云如何運用大模型與小模型來破繭升級2.0

專訪阿里云席明賢，視頻云如何運用大模型與小模型來破繭升級2.0

不久前&#xff0c;LiveVideoStack與阿里云視頻云負責人席明賢&#xff08;花名右賢&#xff09;展開一場深度的對話&#xff0c;一個是圈內專業的社區媒體&#xff0c;一個是20年的IT老兵&#xff0c;雙方有交集、有碰撞、有火花。 面對風云變幻的內外環境&#xff0c;阿里云…
閱讀更多...
未來數字銀行的樣子

未來數字銀行的樣子

對銀行長期發展來講&#xff0c;這意味著將關閉和減少 低效率的實體分行&#xff0c;加速向數字化發展。實現成本節省和 IT 預算提效的需求&#xff0c;將為數字柜臺和銀行代理點創造新的機遇。 一個嶄新的世界&#xff1a;未來數字銀行趨勢圖 現在是銀行迎頭趕上并為客戶提供超…
閱讀更多...
拿來即用，自己封裝的 axios

拿來即用，自己封裝的 axios

文章目錄 一、需求二、分析1. 安裝axios2. 新建一個 ts 文件&#xff0c;封裝 axios3. store 存放 token 信息4. 使用5. 文件 type.js 一、需求 在日常開發中&#xff0c;我們會經常用到 axios &#xff0c;那么如何在自己的項目中自己封裝 axios 二、分析 1. 安裝axios np…
閱讀更多...
jenkins使用

jenkins使用

安裝插件 maven publish over ssh publish over ssh 會將打包后的jar包&#xff0c;通過ssh推送到指定的服務器上&#xff0c;&#xff0c;在jenkins中設置&#xff0c;推送后腳本&#xff0c;實現自動部署jar包&#xff0c;&#xff0c; 裝了這個插件之后&#xff0c;可以在項…
閱讀更多...
最新文章

Copyright @ 2022~2023