K均值聚類是一種常用的無監督學習算法,用于將一組數據點分成不同的簇(clusters),以便數據點在同一簇內更相似,而不同簇之間差異較大。K均值聚類的目標是通過最小化數據點與所屬簇中心之間的距離來形成簇。
當我們要預測的是一個離散值時,做的工作就是“分類”。例如,要預測一個孩子能否成為優秀的運動員,其實就是要將他分到“好苗子”(能成為優秀的運動員)或“普通孩子”(不能成為優秀運動員)的類別。當我們要預測的是一個連續值時,做的工作就是“回歸”。
例如,預測一個孩子將來成為運動員的指數,計算得到的是 0.99 或者 0.36 之類的數值。機器學習模型還可以將訓練集中的數據劃分為若干個組,每個組被稱為一個“簇(cluster)”。
這些自動形成的簇,可能對應著不同的潛在概念,例如“籃球苗子”、“長跑苗子”。這種學習方式被稱為“聚類(clusting)”,它的重要特點是在學習過程中不需要用標簽對訓練樣本進行標注。也就是說,學習過程能夠根據現有訓練集自動完成分類(聚類)。
根據訓練數據是否有標簽,我們可以將學習劃分為監督學習和無監督學習。
前面介紹的 K近鄰、支持向量機都是監督學習,提供有標簽的數據給算法學習,然后對數據分類。而聚類是無監督學習,事先并不知道分類標簽是什么,直接對數據分類。
舉一個簡單的例子,有 100 粒豆子,如果已知其中 40 粒為綠豆,40 粒為大豆,根據上述標簽,將剩下的 20 粒豆子劃分為綠豆和大豆則是監督學習。
針對上述問題可以使用 K 近鄰算法,計算當前待分類豆子的大小,并找出距離其最近的 5 粒豆子的大小,判斷這 5 粒豆子中哪種豆子最多,將當前豆子判定為數量最多的那一類豆子類別。
同樣,有 100 粒豆子,我們僅僅知道這些豆子里有兩個不同的品種,但并不知道到底是什么品種。此時,可以根據豆子的大小、顏色屬性,或者根據大小和顏色的組合屬性,將其劃分為兩個類型。在此過程中,我們沒有使用已知標簽,也同樣完成了分類,此時的分類是一種無監督學習。
聚類是一種無監督學習,它能夠將具有相似屬性的對象劃分到同一個集合(簇)中。聚類方法能夠應用于所有對象,簇內的對象越相似,聚類算法的效果越好。
理論基礎
本節首先用一個實例來介紹 K 均值聚類的基本原理,在此基礎上介紹 K 均值聚類的基本步驟,最后介紹一個二維空間下的 K 均值聚類示例。
分豆子
假設有 6 粒豆子混在一起,我們可以在不知道這些豆子類別的情況下,將它們按照直徑大小劃分為兩類。
經過測量,以 mm(毫米)為單位,這些豆子的直徑大小分別為 1、2、3、10、20、30。下面將它們標記為 A、B、C、D、E、F,并進行分類操作。
第 1 步:隨機選取兩粒參考豆子。例如,隨機將直徑為 1mm 的豆子 A 和直徑為 2 mm 的豆子 B 作為分類參考豆子。
第 2 步:計算每粒豆子的直徑距離豆子 A 和豆子 B 的距離。距離哪個豆子更近,就將新豆子劃分在哪個豆子所在的組。使用直徑作為距離計算依據時,計算結果如表 22-1 所示。

在本步驟結束時,6 粒豆子被劃分為以下兩組。
- 第 1 組:只有豆子 A。
- 第 2 組:豆子 B、C、D、E、F,共 5 粒豆子。
第 3 步:分別計算第 1 組豆子和第 2 組豆子的直徑平均值。然后,將各個豆子按照與直徑
平均值的距離大小分組。
- 計算第 1 組豆子的平均值 AV1 = 1mm。
- 計算第 2 組豆子的平均值 AV2 = (2+3+10+20+30)/5 = 13mm。
得到上述平均值以后,對所有的豆子再次分組:
- 將平均值 AV1 所在的組,標記為 AV1 組。
- 將平均值 AV2 所在的組,標記為 AV2 組。
計算各粒豆子距離平均值 AV1 和 AV2 的距離,并確定分組,如表 22-2 所示。
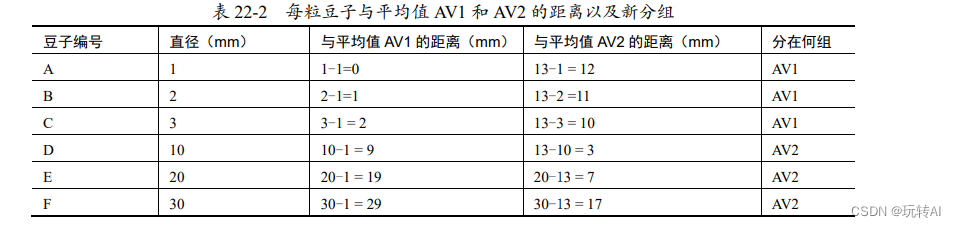
距離平均值 AV1 更近的豆子,就被劃分為 AV1 組;距離平均值 AV2 更近的豆子,就被劃分為 AV2 組。現在,6 粒豆子的分組情況為:
- AV1 組:豆子 A、豆子 B、豆子 C。
- AV2 組:豆子 D、豆子 E、豆子 F。
第4 步:重復第 3 步,直到分組穩定不再發生變化,即可認為分組完成。
在本例中,重新計算 AV1 組的平均值 AV41、AV2 組的平均值 AV42,依次計算每個豆子與平均值 AV41 和 AV42 的距離,并根據該距離重新劃分分組。按照與第 3 步相同的方法,重新計算平均值并分組后,6 粒豆子的分組情況為:
- AV41 組:豆子 A、豆子 B、豆子 C。
- AV42 組:豆子 D、豆子 E、豆子 F。
與上一次的分組相比,并未發生變化,我們就認為分組完成了。
我們將直徑較小的那一組稱為“小豆子”,直徑較大的那一組稱為“大豆子”。
當然,本例是比較極端的例子,數據很快就實現了收斂,在實際處理中可能需要進行多輪的迭代才能實現數據的收斂,分類不再發生變化。
K 均值聚類函數
OpenCV 提供了函數 cv2.kmeans()來實現 K 均值聚類。該函數的語法格式為:
retval, bestLabels, centers=cv2.kmeans(data, K, bestLabels, criteria,
attempts, flags)
式中各個參數的含義為:
-
data:輸入的待處理數據集合,應該是 np.float32 類型,每個特征放在單獨的一列中。
-
K:要分出的簇的個數,即分類的數目,最常見的是 K=2,表示二分類。
-
bestLabels:表示計算之后各個數據點的最終分類標簽(索引)。實際調用時,參數bestLabels 的值設置為 None。
-
criteria:算法迭代的終止條件。當達到最大循環數目或者指定的精度閾值時,算法停止繼續分類迭代計算。該參數由 3 個子參數構成,分別為 type、max_iter 和 eps。
type 表示終止的類型,可以是三種情況,分別為:- cv2.TERM_CRITERIA_EPS:精度滿足 eps 時,停止迭代。
- cv2.TERM_CRITERIA_MAX_ITER:迭代次數超過閾值 max_iter 時,停止迭代。
- cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER:上述兩個條件中的
任意一個滿足時,停止迭代。
-
max_iter:最大迭代次數。
-
eps:精確度的閾值。
-
attempts:在具體實現時,為了獲得最佳分類效果,可能需要使用不同的初始分類值進
行多次嘗試。指定 attempts 的值,可以讓算法使用不同的初始值進行多次(attempts 次)
嘗試。 -
flags:表示選擇初始中心點的方法,主要有以下 3 種。
- cv2.KMEANS_RANDOM_CENTERS:隨機選取中心點。
- cv2.KMEANS_PP_CENTERS:基于中心化算法選取中心點。
- cv2.KMEANS_USE_INITIAL_LABELS:使用用戶輸入的數據作為第一次分類中心點;
如果算法需要嘗試多次(attempts 值大于 1 時),后續嘗試都是使用隨機值或者半隨
機值作為第一次分類中心點。
返回值的含義為:
-
retval:距離值(也稱密度值或緊密度),返回每個點到相應中心點距離的平方和。
-
bestLabels:各個數據點的最終分類標簽(索引)。
-
centers:每個分類的中心點數據。
示例:有一堆米粒,按照長度和寬度對它們分類。
為了方便理解,假設米粒有兩種,其中一種是 XM,另外一種是 DM。它們的直徑不一樣,XM 的長和寬都在[0, 20]內,DM 的長和寬都在[40, 60]內。使用隨機數模擬兩種米粒的長度和寬度,并使用函數 cv2.kmeans()對它們分類。
根據題目要求,主要步驟如下:
(1)隨機生成兩組米粒的數據,并將它們轉換為函數 cv2.kmeans()可以處理的形式。
(2)設置函數 cv2.kmeans()的參數形式。
(3)調用函數 cv2.kmeans()。
(4)根據函數 cv2.kmeans()的返回值,確定分類結果。
(5)繪制經過分類的數據及中心點,觀察分類結果。
代碼如下:
import numpy as np
import cv2
from matplotlib import pyplot as plt
# 隨機生成兩組數值
# xiaomi 組,長和寬都在[0,20]內
xiaomi = np.random.randint(0,20,(30,2))
#dami 組,長和寬的大小都在[40,60]dami = np.random.randint(40,60,(30,2))
# 組合數據
MI = np.vstack((xiaomi,dami))
# 轉換為 float32 類型
MI = np.float32(MI)
# 調用 kmeans 模塊
# 設置參數 criteria 值
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
# 調用 kmeans 函數
ret,label,center=cv2.kmeans(MI,2,None,criteria,10,cv2.KMEANS_RANDOM_CENTERS)
'''
#打印返回值
print(ret)
print(label)
print(center)
'''
# 根據 kmeans 的處理結果,將數據分類,分為 XM 和 DM 兩大類
XM = MI[label.ravel()==0]
DM = MI[label.ravel()==1]
# 繪制分類結果數據及中心點
plt.scatter(XM[:,0],XM[:,1],c = 'g', marker = 's')
plt.scatter(DM[:,0],DM[:,1],c = 'r', marker = 'o')
plt.scatter(center[0,0],center[0,1],s = 200,c = 'b', marker = 'o')
plt.scatter(center[1,0],center[1,1],s = 200,c = 'b', marker = 's')
plt.xlabel('Height'),plt.ylabel('Width')
plt.show()
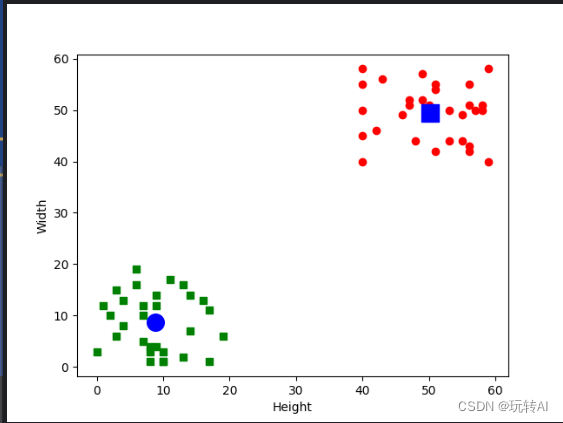
右上方的小方塊是標簽為“0”的數據點,左下方的圓點是標簽為“1”的
數據點。右上方稍大的圓點是標簽“0”的數據組的中心點;左下方稍大的方塊是標簽為“1”的數據組的中心點。




:機器學習入門的概念)


)


方法并行執行多個請求)





)


