👨?🎓作者簡介：一位即將上大四，正專攻機器學習的保研er
🌌上期文章：機器學習&&深度學習——注意力分數（詳細數學推導+代碼實現）
📚訂閱專欄：機器學習&&深度學習
希望文章對你們有所幫助

引入

在深度學習中，經常使用CNN和RNN對序列進行編碼。有了自注意力之后，我們將詞元序列輸入注意力池化中，以便同一組詞元同時充當查詢、鍵和值。具體來說，每個查詢都會關注所有的鍵－值對并生成一個注意力輸出。由于查詢、鍵和值來自同一組輸入，因此被稱為自注意力（self-attention）。下面將使用自注意力進行序列編碼。

import math
import torch
from torch import nn
from d2l import torch as d2l

自注意力

給定一個由詞元組成的序列：
$$\begin{gathered} x_1,...,x_n \\ 其中任意x_i\in R^d \end{gathered}$$
該序列的自注意力輸出為一個長度相同的序列：
$$\begin{gathered} y_1,...,y_n \\ 其中y_i=f(x_i,(x_1,x_1),...,(x_n,x_n))\in R^d \end{gathered}$$
自注意力就是這樣，任意的xi都是既當key，又當value，還當query。
下面的代碼片段是基于多頭注意力對一個張量完成自注意力的計算，張量形狀為（批量大小，時間步數目或詞元序列長度，d）。輸出與輸入的張量形狀相同。
而在此之前，簡單講解下多頭注意力，接著基于多頭注意力實現自注意力。

多頭注意力

當給定相同的查詢、鍵和值的集合時，我們希望模型可以基于相同的注意力機制學習到不同的行為，然后將不同的行為作為知識組合起來，捕獲序列內各種范圍的依賴關系。因此允許注意力機制組合使用查詢、鍵和值的不同子空間表示是有益的。
因此，與其只使用一個注意力池化，我們可以獨立學習得到h組不同的線性投影來變換查詢、鍵和值。然后，這h組變換后的查詢、鍵和值將并行地送到注意力池化中。最后將這h個注意力池化的輸出拼接在一起，并通過另一可以學習的線性投影進行變換，來產生最終輸出。這就是多頭注意力（multihead attention），如下圖所示：

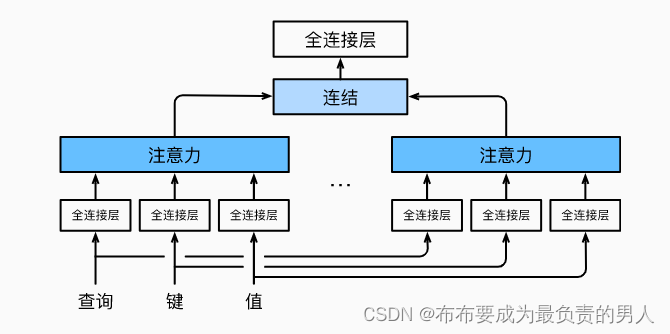
而多頭注意力的實現過程通常使用的是縮放點積注意力來作為每一個注意力頭，我們設定：
$$p_q=p_k=p_v=p_o/h$$
值得注意的是，如果將查詢、鍵和值的線性變化的輸出數量設置為：
$$p_{q}h=p_{k}h=p_{v}h=p_o$$
就可以并行計算h個頭，下面代碼中的po是通過num_hiddens指定的。

代碼如下：

#@save
class MultiHeadAttention(nn.Module):"""多頭注意力"""def __init__(self, key_size, query_size, value_size, num_hiddens,num_heads, dropout, bias=False, **kwargs):super(MultiHeadAttention, self).__init__(**kwargs)self.num_heads = num_headsself.attention = d2l.DotProductAttention(dropout)self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)def forward(self, queries, keys, values, valid_lens):# queries，keys，values的形狀:# (batch_size，查詢或者“鍵－值”對的個數，num_hiddens)# valid_lens　的形狀:# (batch_size，)或(batch_size，查詢的個數)# 經過變換后，輸出的queries，keys，values　的形狀:# (batch_size*num_heads，查詢或者“鍵－值”對的個數，# num_hiddens/num_heads)queries = transpose_qkv(self.W_q(queries), self.num_heads)keys = transpose_qkv(self.W_k(keys), self.num_heads)values = transpose_qkv(self.W_v(values), self.num_heads)if valid_lens is not None:# 在軸0，將第一項（標量或者矢量）復制num_heads次，# 然后如此復制第二項，然后諸如此類。valid_lens = torch.repeat_interleave(valid_lens, repeats=self.num_heads, dim=0)# output的形狀:(batch_size*num_heads，查詢的個數，# num_hiddens/num_heads)output = self.attention(queries, keys, values, valid_lens)# output_concat的形狀:(batch_size，查詢的個數，num_hiddens)output_concat = transpose_output(output, self.num_heads)return self.W_o(output_concat)#@save
def transpose_qkv(X, num_heads):"""為了多注意力頭的并行計算而變換形狀"""# 輸入X的形狀:(batch_size，查詢或者“鍵－值”對的個數，num_hiddens)# 輸出X的形狀:(batch_size，查詢或者“鍵－值”對的個數，num_heads，# num_hiddens/num_heads)X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)# 輸出X的形狀:(batch_size，num_heads，查詢或者“鍵－值”對的個數,# num_hiddens/num_heads)X = X.permute(0, 2, 1, 3)# 最終輸出的形狀:(batch_size*num_heads,查詢或者“鍵－值”對的個數,# num_hiddens/num_heads)return X.reshape(-1, X.shape[2], X.shape[3])#@save
def transpose_output(X, num_heads):"""逆轉transpose_qkv函數的操作"""X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])X = X.permute(0, 2, 1, 3)return X.reshape(X.shape[0], X.shape[1], -1)

基于多頭注意力實現自注意力

num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,num_hiddens, num_heads, 0.5)
attention.eval()

可以輸出驗證一下：

batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
print(attention(X, X, X, valid_lens).shape)

輸出結果：

torch.Size([2, 4, 100])

比較CNN、RNN和self-attention

首先看這個圖：

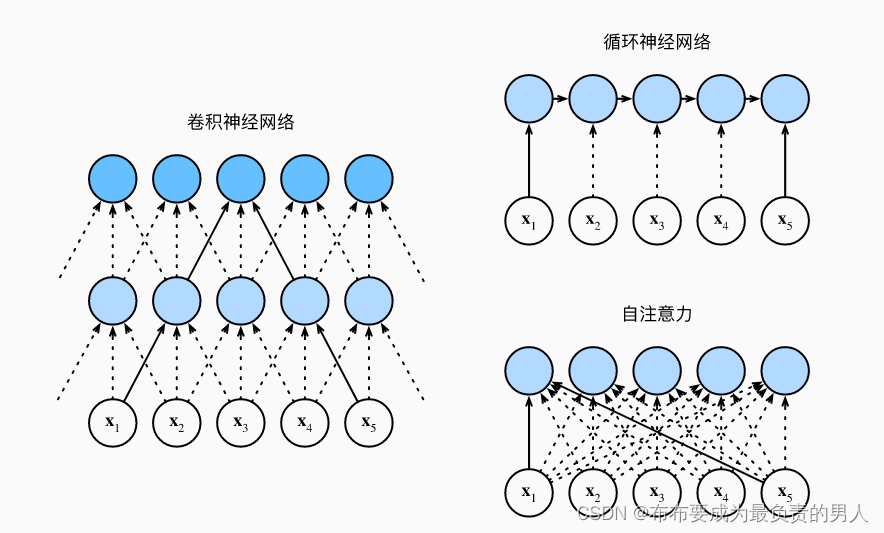
接下來進行CNN、RNN以及self-attention三個架構的比較，首先這三個架構目標都是要將n個詞元組成的序列映射到另一個長度相同的序列，其中的每個輸入詞元或輸出詞元都由d維向量表示。我們的比較將基于計算的復雜性、順序操作和最大路徑長度，先給出結論再進行剖析解釋。
我們首先要知道，順序操作會妨礙并行計算，而任意的序列位置組合之間的路徑越短，則能更輕松地學習序列中的遠距離依賴關系。

結論

	計算復雜度	并行度	最大路徑長度
CNN	O(knd2)	O(n)	O(n/k)
RNN	O(nd2)	O(1)	O(n)
self-attention	O(n2d)	O(n)	O(1)

剖析——CNN

考慮一個卷積核大小為k的卷積層，由于序列長度是n，輸入和輸出的通道數量都是d，所以卷積層的計算復雜度為O(knd²)。而如上圖所示，可以看出CNN網絡是分層的，因此會有O(1)個順序操作，那么這代表著通道可以并行執行n個詞元，那么并行度就是O(n)。
上圖中可以看出k=3，因為這樣剛好就使得x1和x5處于這個卷積核大小為3的雙層卷積神經網絡的感受野內。因此最大的路徑長度一定是不會超過n/k的，下標為n的也會因為卷積核被限制到一個感受野內，因此可以知道最大路徑長度為O(n/k)。

剖析——RNN

當更新RNN的隱狀態時，d×d權重矩陣和d維隱狀態的乘法計算復雜度為O(d²)，再加上序列長度為n，因此RNN的計算復雜度為O(nd²)，由上圖也可以看出n個序列的順序操作是沒辦法并行化的，則并行度為O(1)，最大路徑長度是O(n)（可以理解成當我們要組合y1和yn的時候，這時候長度為n）。

剖析——self-attention

查詢、鍵、值都是n×d矩陣。計算過程為：n×d矩陣乘以d×n矩陣，之后得到的n×n矩陣再乘以n×d矩陣，因此自注意力有O(n²d)的計算復雜度。而上圖展示了自注意力的強大，O(n)的并行度顯而易見，同時最大路徑長度是O(1)，因為他們可以任意組合。

總結

總而言之，卷積神經網絡和自注意力都擁有并行計算的優勢，而且自注意力的最大路徑長度最短。
但是因為其計算復雜度是關于序列長度的二次方，所以在很長的序列中計算會非常慢。

位置編碼

在處理詞元序列時，循環神經網絡是逐個的重復地處理詞元的，而自注意力則因為并行計算而放棄了順序操作。為了使用序列的順序信息，通過在輸入表示中添加位置編碼來注入絕對的或相對的位置信息。
位置編碼可以通過學習得到也可以直接固定得到，下面講解基于正弦函數和余弦函數的固定位置編碼。
假設輸入表示X∈R^n×d包含一個序列中n個詞元的d維嵌入表示。位置編碼使用相同形狀的位置嵌入矩陣P∈R^n×d輸出X+P，矩陣第[i,2j]（偶數列）和[i,2j+1]（奇數列）列上的元素為：
$$\begin{gathered} p_{i,2j}=sin(\frac{i}{10000^{2j/d}}), \\ {p}_{i,2j+1}=cos(\frac{i}{10000^{2j/d}}) \end{gathered}$$
看起來很奇怪，在后面講解的時候就能看出來了，先定義一個類來實現它：

#@save
class PositionalEncoding(nn.Module):"""位置編碼"""def __init__(self, num_hiddens, dropout, max_len=1000):super(PositionalEncoding, self).__init__()self.dropout = nn.Dropout(dropout)# 創建一個足夠長的Pself.P = torch.zeros((1, max_len, num_hiddens))X = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1) / torch.pow(10000, torch.arange(0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)self.P[:, :, 0::2] = torch.sin(X)self.P[:, :, 1::2] = torch.cos(X)def forward(self, X):X = X + self.P[:, :X.shape[1], :].to(X.device)return self.dropout(X)

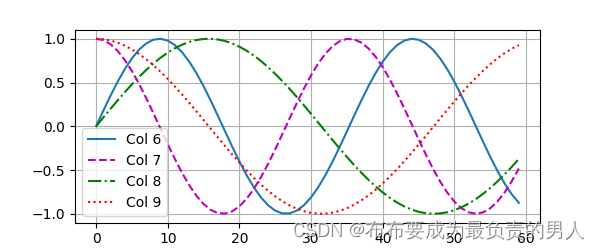
我們可以進行打印圖像，可以清晰看到6、7列比8、9列頻率高，而6與7（8與9同理）由于正余弦函數的相位交替，而導致偏移量不同。

encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
d2l.plt.show()

運行結果：

絕對位置信息

其實就是二進制了，想象一下0-7的二進制表示是各不相同的，而且容易知道：較高比特位的交替頻率低于較低比特位（而使用三教函數的話輸出的是浮點數，顯然會更省空間）。

相對位置信息

除了捕獲絕對位置信息之外，上述的位置編碼還允許模型學習得到輸入序列中相對位置信息。這是因為對于任何確定的位置偏移σ，位置i+σ處的位置編碼可以線性投影位置i處的位置編碼來表示。
用數學來表示：
$$\begin{gathered} 令w_j=1/10000^{2j/d}，對于任何確定的位置偏移\sigma ： \\ \left[\begin{array}{cc}cos(\sigma w_j)& sin(\sigma w_j)\\ ?sin(\sigma w_j)& cos(\sigma w_j)\end{array}\right]\left[\begin{array}{c}{p}_{i,2j}\\ p_{i,2j+1}\end{array}\right] \\ =\left[\begin{array}{c}cos(\sigma w_j)sin(i{w}_j)+sin(\sigma w_j)cos(i{w}_j)\\ ?sin(\sigma w_j)sin(i{w}_j)+cos(\sigma w_j)cos(i{w}_j)\end{array}\right] \\ =\left[\begin{array}{c}sin((i+\sigma )w_j)\\ cos((i+\sigma )w_j)\end{array}\right]——積化和差 \\ =\left[\begin{array}{c}{p}_{i+\sigma ,2j}\\ p_{i+\sigma ,2j+1}\end{array}\right] \end{gathered}$$
2×2投影矩陣不依賴于任何位置的索引i。

小結

1、在自注意力中，查詢、鍵和值都來自同一組輸入。
2、卷積神經網絡和自注意力都擁有并行計算的優勢，而且自注意力的最大路徑長度最短。但是因為其計算復雜度是關于序列長度的二次方，所以在很長的序列中計算會非常慢。
3、為了使用序列的順序信息，可以通過在輸入表示中添加位置編碼，來注入絕對的或相對的位置信息。