1，理論

最簡單的方式利用向量進行求解

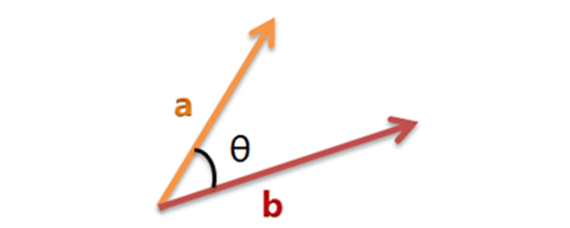
?如圖可得：

cosθ=a*b/（|a|*|b|）

已知三點坐標，很容易可以得到兩向量之積a*b，以及每個的模值

2，四個角度求解過程

1. 首先，我們定義了四個坐標點pointA、pointB、pointC、pointD，這些點構成了一個四邊形。

2. 接下來，我們調用calculateAngle方法來計算四邊形的每個內角。calculateAngle方法接受三個參數，分別是三個點的坐標，用于計算夾角。

3. 在calculateAngle方法中，我們首先計算向量1的x和y分量，即點p1與點p2之間的向量。然后計算向量2的x和y分量，即點p3與點p2之間的向量。

4. 接著，我們計算向量1和向量2的點積，即dotProduct = vector1x * vector2x + vector1y * vector2y。

5. 計算向量1和向量2的模，即各自的長度，使用Math.sqrt()方法計算平方根。

6. 接下來，我們計算夾角的余弦值，即cosTheta = dotProduct / (magnitude1 * magnitude2)。

7. 最后，我們使用Math.acos()方法計算夾角的弧度值，并將其轉換為度數，使用Math.toDegrees()方法。

8. 在main方法中，我們依次計算四邊形的四個內角，并將其打印輸出。

3，代碼實現

import java.awt.geom.Point2D;public class QuadrilateralAngles {public static void main(String[] args) {// 四個坐標點Point2D.Double pointA = new Point2D.Double(0, 0);Point2D.Double pointB = new Point2D.Double(1, 1);Point2D.Double pointC = new Point2D.Double(0, 1);Point2D.Double pointD = new Point2D.Double(-1, 0);// 計算四邊形的四個內角double angleA = calculateAngle(pointD, pointA, pointB);double angleB = calculateAngle(pointA, pointB, pointC);double angleC = calculateAngle(pointB, pointC, pointD);double angleD = calculateAngle(pointC, pointD, pointA);// 輸出結果System.out.println("Angle A: " + angleA);System.out.println("Angle B: " + angleB);System.out.println("Angle C: " + angleC);System.out.println("Angle D: " + angleD);}// 計算夾角的方法public static double calculateAngle(Point2D.Double p1, Point2D.Double p2, Point2D.Double p3) {// 計算向量1的x和y分量double vector1x = p1.getX() - p2.getX();double vector1y = p1.getY() - p2.getY();// 計算向量2的x和y分量double vector2x = p3.getX() - p2.getX();double vector2y = p3.getY() - p2.getY();// 計算向量1和向量2的點積double dotProduct = vector1x * vector2x + vector1y * vector2y;// 計算向量1和向量2的模double magnitude1 = Math.sqrt(vector1x * vector1x + vector1y * vector1y);double magnitude2 = Math.sqrt(vector2x * vector2x + vector2y * vector2y);// 計算兩向量夾角的余弦值double cosTheta = dotProduct / (magnitude1 * magnitude2);// 計算夾角的弧度值double theta = Math.acos(cosTheta);// 將弧度轉換為度數并返回return Math.toDegrees(theta);}
}