許久不見~
本節我們延續上一節的話題來看看卷積神經網絡的架構，看看具體的卷積、池化等操作

---

卷積神經網絡詳解：從基礎操作到整體架構

一、卷積操作：特征提取的核心

卷積是卷積神經網絡（CNN）的核心操作，靈感來源于人類視覺系統。在圖像處理中，卷積可表示為：

$$(I?K)(i,j)=\sum _m\sum _{n}I(i+m,j+n)?K(m,n)$$

其中：

• $I$ 是輸入圖像矩陣
• $K$ 是卷積核（濾波器）
• $(i,j)$ 是輸出位置坐標

卷積過程圖解：

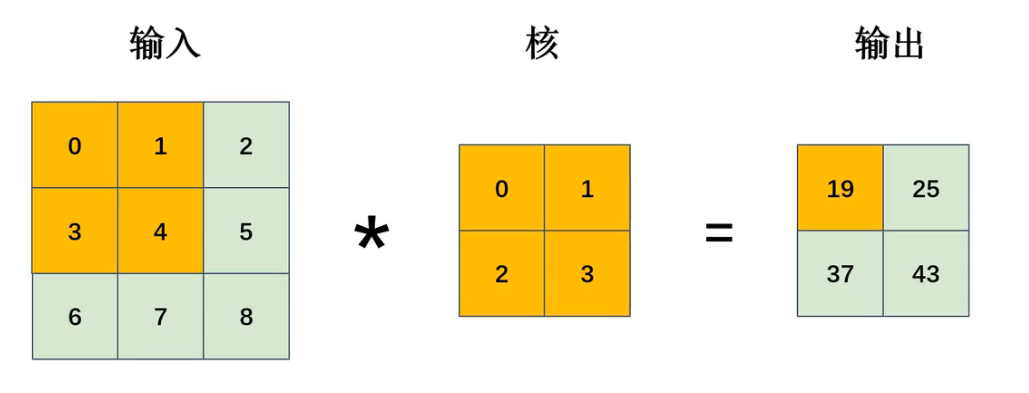
計算示例（左上角位置）：
$$(0\times 0)+(1\times 1)+(3\times 2)+(4\times 3)=19$$
簡單來說就是對應相乘然后求和

卷積核本質是特征檢測器，不同核可提取邊緣、紋理等特征：

• 垂直邊緣檢測核：$\left[\begin{array}{ccc}1& 0& ?1\\ 1& 0& ?1\\ 1& 0& ?1\end{array}\right]$
• 水平邊緣檢測核：$\left[\begin{array}{ccc}1& 1& 1\\ 0& 0& 0\\ ?1& ?1& ?1\end{array}\right]$

至于特征是什么，你就當做是屬性或者本質來理解吧

---

二、步幅（Stride）：控制計算密度

步幅定義卷積核每次移動的像素數。設步幅為$S$：

• $S=1$：滑動間隔1像素（輸出尺寸最大）
• $S=2$：滑動間隔2像素（輸出尺寸減半）

步幅影響圖解：

S=1時移動路徑：    S=2時移動路徑：
→→→→→            → → → 
↓↓             ↓   ↓
→→→→→            → → → 
↓↓
→→→→→

數學意義：步幅增加會降低特征圖分辨率，但能顯著減少計算量，適用于深層網絡。

---

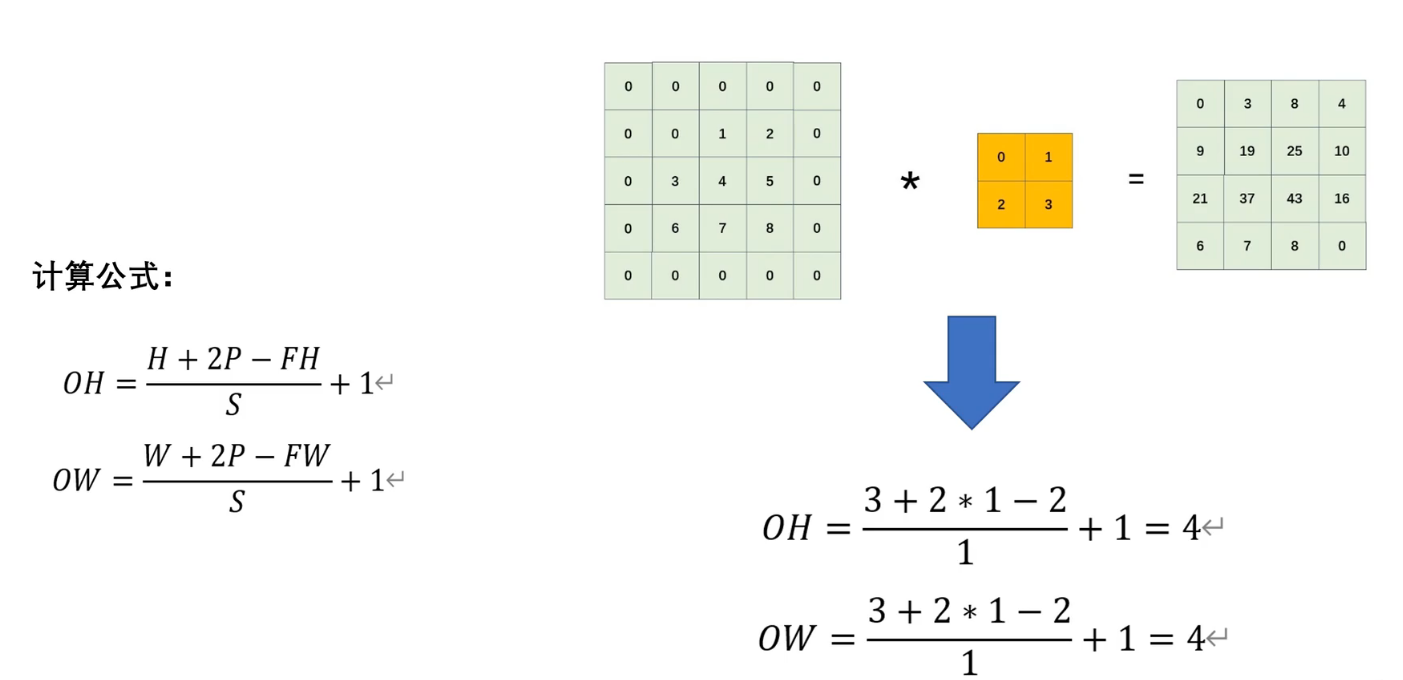
三、填充（Padding）：邊界信息保護

填充是在輸入圖像邊緣添加像素（通常為0），解決兩個核心問題：

1. 邊界信息丟失（角落像素參與計算次數少）
2. 輸出尺寸收縮

常用填充模式：

類型	公式	輸出尺寸	特點
Valid	$P=0$	$\frac{W?F}{S}+1$	無填充，輸出縮小
Same	$P=\frac{F?1}{2}$	$W$	輸入輸出同尺寸

填充量$P$的計算：
$$P=?\frac{F?1}{2}?$$
其中$F$為卷積核尺寸

填充效果示例（3x3核，Same填充）：

原始輸入：    填充后（P=1）：
1 2 3       0 0 0 0 0
4 5 6   →   0 1 2 3 0
7 8 9       0 4 5 6 00 7 8 9 00 0 0 0 0

---

四、池化層：空間信息壓縮

池化層通過降采樣減少參數量，增強特征不變性。

1. 最大值池化（Max Pooling）

$$\text{輸出}(i,j)=\underset{m,n\in \mathcal{R}}{\max }\text{輸入}(i\times S+m,j\times S+n)$$

可以這樣來理解，在一個區域內挑選最大的

• 

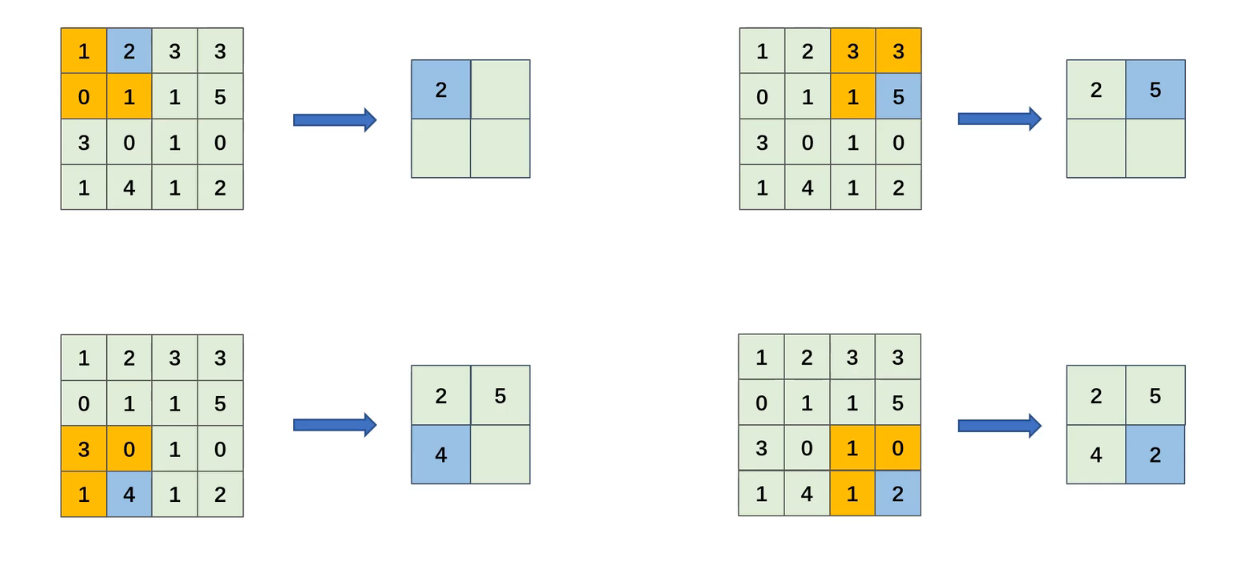
• 歷史：1980年福島邦彥在Neocognitron首次提出，1998年LeNet-5正式應用

• 特點：保留顯著特征，對噪聲魯棒

2. 平均池化（Average Pooling）

$$\text{輸出}(i,j)=\frac{1}{|\mathcal{R}|}\sum _{m,n\in \mathcal{R}}\text{輸入}(i\times S+m,j\times S+n)$$
平均池化就是將這個區域內的值求平均數

• 

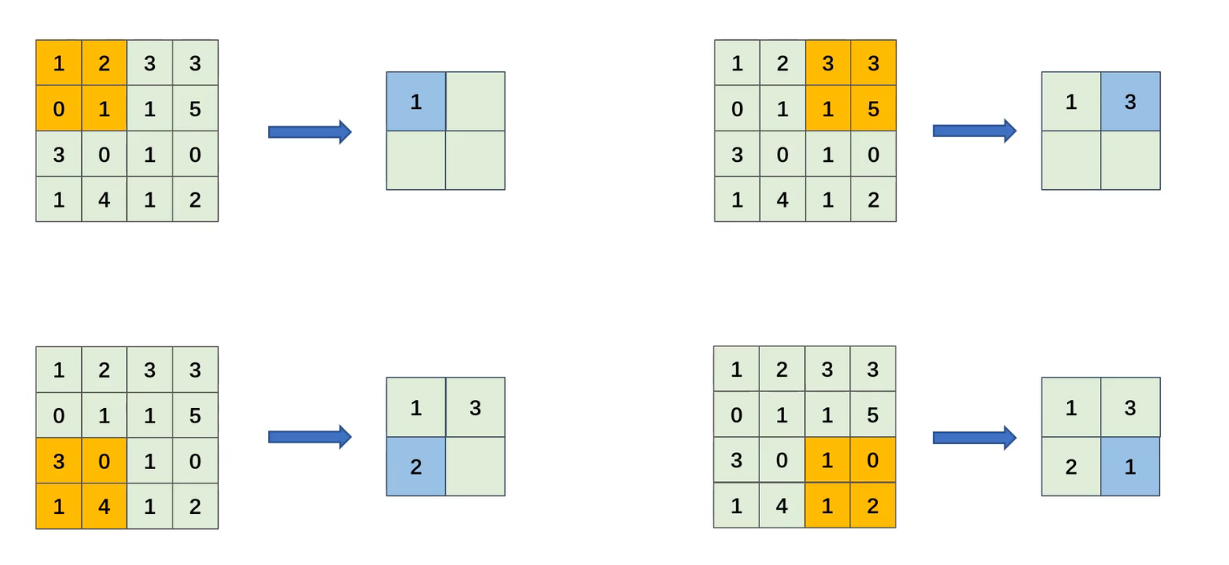
• 歷史：2012年AlexNet首次大規模應用，緩解過擬合

• 特點：保留整體特征分布，平滑特征圖

池化過程圖解（2x2池化窗口，S=2）：

輸入矩陣：        最大值池化：     平均池化：
[1 5 0 2]        [5  2]         [3.0  1.5]
[3 2 4 1]   →    [4  3]         [3.5  2.5]
[7 0 3 5]        [7  5]         [3.5  4.0]
[2 6 1 4]                          

在這里我們將池化的核叫做感受眼 池化只算一種操作而不是卷積網絡中的一層，但是它依舊會影響輸入輸出的特征圖大小

---

五、輸出特征圖計算通式

給定參數：

• 輸入尺寸：$W\times H\times D_{in}$
• 卷積核尺寸：$FH\times FW\times D_{in}$
• 卷積核通道數:$D$
• 步幅：$S$
• 填充：$P$

輸出特征圖尺寸：通道數由卷積核的通道數決定

計算示例：

• 輸入：$224\times 224\times 3$ 圖像
• 卷積核：$7\times 7\times 3$，$K=64$
• $S=2$，$P=3$
• 輸出：$W_{out}=?(224?7+6)/2?+1=112$
• 最終輸出：$112\times 112\times 64$

---

六、多通道卷積運算

多通道卷積是CNN處理彩色圖像的關鍵，運算過程分三步：

1. 輸入結構：$D_{in}$通道輸入（如RGB三通道）
   $$\text{輸入}\in {\mathbb{R}}^{W\times H\times D_{in}}$$

2. 卷積核結構：每個卷積核包含$D_{in}$個通道的權重
   $$K_k\in {\mathbb{R}}^{F\times F\times D_{in}}(k=1,2,...,K)$$

3. 計算過程：
   $${\text{輸出}}_k(i,j)=\sum _{d=1}^{D_{in}}\left(\sum _{m=0}^{F?1}\sum _{n=0}^{F?1}{I}_d(i+m,j+n)?K_k^{(d)}(m,n)\right)+b_k$$

多通道卷積示意圖：

輸入通道（3通道）      卷積核組（2個核）
[ R ]               [ K1_R ] [ K2_R ]
[ G ]          *    [ K1_G ] [ K2_G ]  = 輸出特征圖（2通道）
[ B ]               [ K1_B ] [ K2_B ]

為什么會是這樣呢？對于輸入的3通道 ，每一個通道會和卷積核的一個通道進行卷積計算然后進行疊加，得到一個通道的輸出，卷積核有多少的通道就會進行多少次這樣的計算，因此由卷積核的通道（核的數量）決定本層的輸出通道數

---

七、卷積神經網絡整體架構

典型CNN包含以下層級結構：

1. 輸入層

• 接收$W\times H\times C$張量
• 預處理：歸一化、數據增強

2. 卷積塊（重復N次）

這一塊代碼你可能還看不懂，沒有關系，我們下一節具體來講解

# 典型卷積塊代碼實現
def conv_block(x, filters, kernel_size=3):x = Conv2D(filters, kernel_size, padding='same')(x)x = BatchNormalization()(x)x = ReLU()(x)return x

• 卷積層：提取局部特征
• 激活函數：引入非線性（常用ReLU：$f(x)=\max (0,x)$）
• 批歸一化：加速訓練

3. 池化層

• 空間降維：通常$2\times 2$窗口，$S=2$
• 位置：每1-2個卷積塊后

4. 全連接層

• 特征整合：將3D特征展平為1D向量
  $$\text{Flatten}:{\mathbb{R}}^{W\times H\times D}\to {\mathbb{R}}^N(N=W\times H\times D)$$
• 分類輸出：Softmax激活函數

5. 經典架構演進

網絡	創新點	深度	Top-5錯誤率
LeNet-5 (1998)	首個實用CNN架構	7層	-
AlexNet (2012)	ReLU/Dropout/多GPU訓練	8層	16.4%
VGG (2014)	3x3小卷積核堆疊	16-19層	7.3%
ResNet (2015)	殘差連接解決梯度消失	50-152層	3.57%

現代CNN架構特征：

• 深度堆疊：16~100+層
• 殘差連接：$H(x)=F(x)+x$
• 瓶頸結構：1x1卷積降維
• 注意力機制：通道/空間注意力
• 輕量化設計：深度可分離卷積

---

八、端到端計算流程示例

以10x10 RGB圖像分類為例：

1. 輸入層：$10\times 10\times 3$
2. 卷積層1：32個$3\times 3$核，S=1，P=1 → $10\times 10\times 32$
3. 池化層1：2x2 MaxPooling, S=2 → $5\times 5\times 32$
4. 卷積層2：64個$3\times 3$核，S=1，P=1 → $5\times 5\times 64$
5. 池化層2：2x2 MaxPooling, S=2 → $2\times 2\times 64$
6. 全連接層：Flatten → $256$神經元
7. 輸出層：Softmax → 類別概率

參數量計算：

• 卷積層1：$(3\times 3\times 3+1)\times 32=896$
• 卷積層2：$(3\times 3\times 32+1)\times 64=18,496$
• 全連接層：$(256+1)\times 10=2,570$
• 總計：21,962參數（傳統神經網絡需數百萬參數）

---

九、卷積神經網絡優勢

1. 局部連接：每個神經元僅連接局部區域，大幅減少參數量
   $$\text{參數量}=(F\times F\times D_{in}+1)\times D_{out}$$

2. 權值共享：同一卷積核在整張圖像滑動，增強泛化能力

3. 平移不變性：池化操作使特征對位置變化魯棒

4. 層次化特征：

   • 淺層：邊緣/紋理
   • 中層：部件組合
   • 深層：語義對象

---

本介紹涵蓋卷積神經網絡核心組件及其數學原理，通過系統闡述，由基礎操作延伸至架構設計，結合公式推導和概念圖解，構建完整的知識體系。實際實現時需結合PyTorch/TensorFlow等框架，通過反向傳播優化卷積核權重。
So,我們下一節來看看經典的神經網絡的參數然后直接進行實戰練習吧~