代碼隨想錄算法訓練營第59天｜動態規劃part16｜583. 兩個字符串的刪除操作、72. 編輯距離、編輯距離總結篇

583. 兩個字符串的刪除操作

583. 兩個字符串的刪除操作

思路：

思路見代碼

代碼：

python

class Solution(object):def minDistance(self, word1, word2):""":type word1: str:type word2: str:rtype: int"""# dp[i][j] 表示word1的0-(i-1)索引的子串與word2的0-(j-1)索引的子串 使得相同所需的最小步數'''dp[i][j]如何推出如果word1[i-1] == word2[j-1]:不需要刪除操作dp[i][j] = dp[i-1][j-1]如果word1[i-1] != word2[j-1]:需要刪除：有兩種情況：1. 僅操作word1子串 2. 僅操作word2子串 3. 操作word1和word2情況1:word1刪除一個字符 dp[i][j] = dp[i][j-1] + 1情況2:word2刪除一個字符 dp[j][i] = dp[i-1][j] + 1情況3:word1和word2各刪除一個字符 dp[i][j] = dp[i-1][j-1] + 2取最小：dp[i][j] = min(情況1, 情況2, 情況3)''''''初始化:dp[0][0] = 0dp[0][j] = jdp[i][0] = i'''dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]for i in range(len(word1)+1):dp[i][0] = ifor j in range(len(word2)+1):dp[0][j] = jprint(dp)for i in range(1, len(word1)+1):for j in range(1, len(word2)+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:dp[i][j] = min(dp[i][j-1] + 1, dp[i-1][j] + 1, dp[i-1][j-1] + 2) print(dp)return dp[-1][-1]

代碼隨想錄：

思路一模一樣，哈哈哈，我終于獨自做對一回了！

72. 編輯距離

72. 編輯距離

思路：

編輯距離終于來了，這道題目如果大家沒有了解動態規劃的話，會感覺超級復雜。

編輯距離是用動規來解決的經典題目，這道題目看上去好像很復雜，但用動規可以很巧妙的算出最少編輯距離。

接下來我依然使用動規五部曲，對本題做一個詳細的分析：

1. 確定dp數組（dp table）以及下標的含義

dp[i][j] 表示以下標i-1為結尾的字符串word1，和以下標j-1為結尾的字符串word2，最近編輯距離為dp[i][j]。

2. 確定遞推公式

在確定遞推公式的時候，首先要考慮清楚編輯的幾種操作，整理如下：

if (word1[i - 1] == word2[j - 1])不操作
if (word1[i - 1] != word2[j - 1])增刪換

也就是如上4種情況。

if (word1[i - 1] == word2[j - 1]) 那么說明不用任何編輯，dp[i][j] 就應該是 dp[i - 1][j - 1]，即dp[i][j] = dp[i - 1][j - 1];

if (word1[i - 1] != word2[j - 1])，此時就需要編輯了，如何編輯呢？

操作一：word1刪除一個元素，那么就是以下標i - 2為結尾的word1 與 j-1為結尾的word2的最近編輯距離 再加上一個操作。

即 dp[i][j] = dp[i - 1][j] + 1;

操作二：word2刪除一個元素，那么就是以下標i - 1為結尾的word1 與 j-2為結尾的word2的最近編輯距離 再加上一個操作。

即 dp[i][j] = dp[i][j - 1] + 1;

這里有同學發現了，怎么都是刪除元素，添加元素去哪了。

word2添加一個元素，相當于word1刪除一個元素, 例如 word1 = “ad” ，word2 = “a”，word1刪除元素’d’ 和 word2添加一個元素’d’，變成word1=“a”, word2=“ad”， 最終的操作數是一樣！ dp數組如下圖所示意的：

操作三：替換元素，word1替換word1[i - 1]，使其與word2[j - 1]相同，此時不用增刪加元素。

可以回顧一下，if (word1[i - 1] == word2[j - 1])的時候我們的操作 是 dp[i][j] = dp[i - 1][j - 1] 對吧。

那么只需要一次替換的操作，就可以讓 word1[i - 1] 和 word2[j - 1] 相同。

所以 dp[i][j] = dp[i - 1][j - 1] + 1;

綜上，當 if (word1[i - 1] != word2[j - 1]) 時取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];
}
else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

3. dp數組如何初始化

再回顧一下dp[i][j]的定義：

dp[i][j] 表示以下標i-1為結尾的字符串word1，和以下標j-1為結尾的字符串word2，最近編輯距離為dp[i][j]。

那么dp[i][0] 和 dp[0][j] 表示什么呢？

dp[i][0] ：以下標i-1為結尾的字符串word1，和空字符串word2，最近編輯距離為dp[i][0]。

那么dp[i][0]就應該是i，對word1里的元素全部做刪除操作，即：dp[i][0] = i;

同理dp[0][j] = j;

所以C++代碼如下：

for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;

4. 確定遍歷順序

從如下四個遞推公式：

dp[i][j] = dp[i - 1][j - 1]
dp[i][j] = dp[i - 1][j - 1] + 1
dp[i][j] = dp[i][j - 1] + 1
dp[i][j] = dp[i - 1][j] + 1
可以看出dp[i][j]是依賴左方，上方和左上方元素的，如圖：

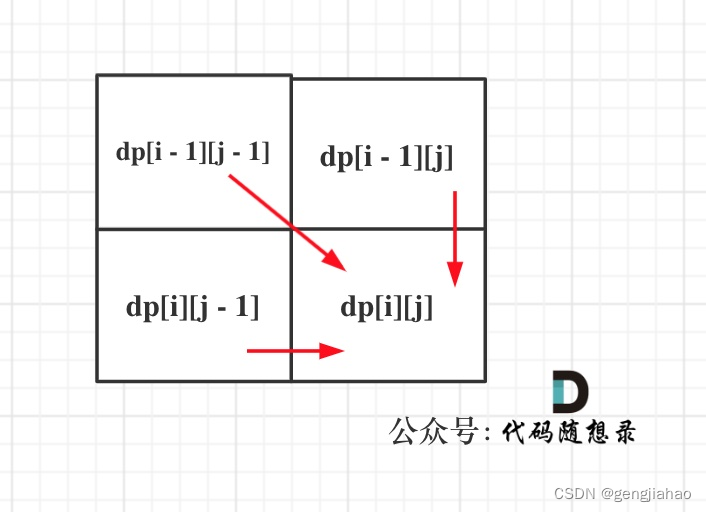
所以在dp矩陣中一定是從左到右從上到下去遍歷。

for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];}else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;}}
}

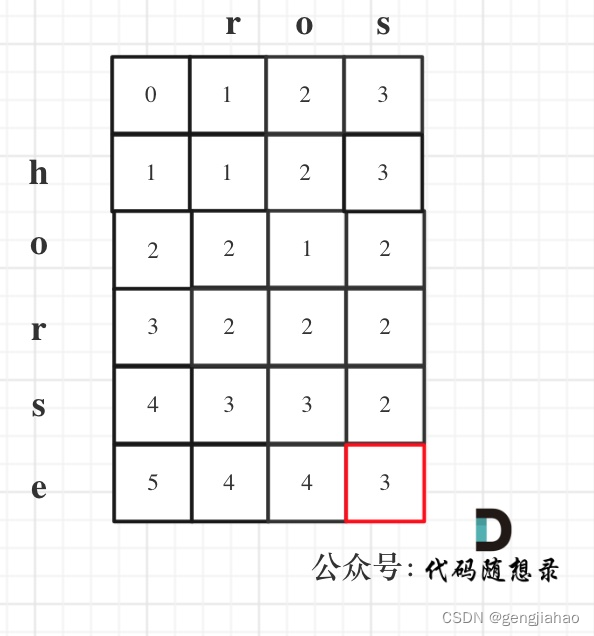
5. 舉例推導dp數組

以示例1為例，輸入：word1 = “horse”, word2 = "ros"為例，dp矩陣狀態圖如下：

代碼：

python

class Solution:def minDistance(self, word1: str, word2: str) -> int:dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]for i in range(len(word1)+1):dp[i][0] = ifor j in range(len(word2)+1):dp[0][j] = jfor i in range(1, len(word1)+1):for j in range(1, len(word2)+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1return dp[-1][-1]

編輯距離總結

鏈接