數據結構的樹存儲結構

之前介紹的所有的數據結構都是線性存儲結構。本章所介紹的樹結構是一種非線性存儲結構，存儲的是具有“一對多”關系的數據元素的集合。

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

? ? ? ?(A) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(B)?

圖 1 樹的示例

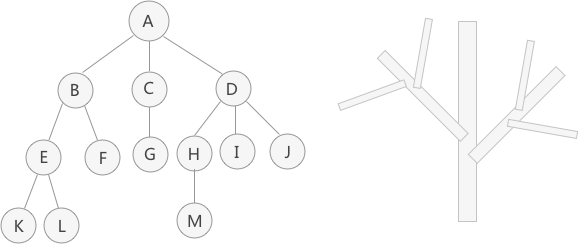
圖 1(A) 是使用樹結構存儲的集合 {A,B,C,D,E,F,G,H,I,J,K,L,M} 的示意圖。對于數據 A 來說，和數據 B、C、D 有關系；對于數據 B 來說，和 E、F 有關系。這就是“一對多”的關系。

將具有“一對多”關系的集合中的數據元素按照圖 1（A）的形式進行存儲，整個存儲形狀在邏輯結構上看，類似于實際生活中倒著的樹（圖 1（B）倒過來），所以稱這種存儲結構為“樹型”存儲結構。

樹的結點

結點：使用樹結構存儲的每一個數據元素都被稱為“結點”。例如，圖 1（A）中，數據元素 A 就是一個結點；

父結點（雙親結點）、子結點和兄弟結點：對于圖 1（A）中的結點 A、B、C、D 來說，A 是 B、C、D 結點的父結點（也稱為“雙親結點”），而 B、C、D 都是 A 結點的子結點（也稱“孩子結點”）。對于 B、C、D 來說，它們都有相同的父結點，所以它們互為兄弟結點。

樹根結點（簡稱“根結點”）：每一個非空樹都有且只有一個被稱為根的結點。圖 1（A）中，結點 A 就是整棵樹的根結點。

樹根的判斷依據為：如果一個結點沒有父結點，那么這個結點就是整棵樹的根結點。

葉子結點：如果結點沒有任何子結點，那么此結點稱為葉子結點（葉結點）。例如圖 1（A）中，結點 K、L、F、G、M、I、J 都是這棵樹的葉子結點。

子樹和空樹

子樹：如圖 1（A）中，整棵樹的根結點為結點 A，而如果單看結點 B、E、F、K、L 組成的部分來說，也是棵樹，而且節點 B 為這棵樹的根結點。所以稱 B、E、F、K、L 這幾個結點組成的樹為整棵樹的子樹；同樣，結點 E、K、L 構成的也是一棵子樹，根結點為 E。

注意：單個結點也是一棵樹，只不過根結點就是它本身。圖 1（A）中，結點 K、L、F 等都是樹，且都是整棵樹的子樹。

知道了子樹的概念后，樹也可以這樣定義：樹是由根結點和若干棵子樹構成的。

空樹：如果集合本身為空，那么構成的樹就被稱為空樹。空樹中沒有結點。

補充：在樹結構中，對于具有同一個根結點的各個子樹，相互之間不能有交集。例如，圖 1（A）中，除了根結點 A，其余元素又各自構成了三個子樹，根結點分別為 B、C、D，這三個子樹相互之間沒有相同的結點。如果有，就破壞了樹的結構，不能算做是一棵樹。

結點的度和層次

對于一個結點，擁有的子樹數（結點有多少分支）稱為結點的度（Degree）。例如，圖 1（A）中，根結點 A 下分出了 3 個子樹，所以，結點 A 的度為 3。

一棵樹的度是樹內各結點的度的最大值。圖 1（A）表示的樹中，各個結點的度的最大值為 3，所以，整棵樹的度的值是 3。

?

結點的層次：從一棵樹的樹根開始，樹根所在層為第一層，根的孩子結點所在的層為第二層，依次類推。對于圖 1（A）來說，A 結點在第一層，B、C、D 為第二層，E、F、G、H、I、J 在第三層，K、L、M 在第四層。

一棵樹的深度（高度）是樹中結點所在的最大的層次。圖 1（A）樹的深度為 4。

如果兩個結點的父結點雖不相同，但是它們的父結點處在同一層次上，那么這兩個結點互為堂兄弟。例如，圖 1（A）中，結點 G 和 E、F、H、I、J 的父結點都在第二層，所以之間為堂兄弟的關系。

有序樹和無序樹

如果樹中結點的子樹從左到右看，誰在左邊，誰在右邊，是有規定的，這棵樹稱為有序樹；反之稱為無序樹。

在有序樹中，一個結點最左邊的子樹稱為"第一個孩子"，最右邊的稱為"最后一個孩子"。

拿圖 1（A）來說，如果是其本身是一棵有序樹，則以結點 B 為根結點的子樹為整棵樹的第一個孩子，以結點 D 為根結點的子樹為整棵樹的最后一個孩子。

森林

由 m（m >= 0）個互不相交的樹組成的集合被稱為森林。圖 1（A）中，分別以 B、C、D 為根結點的三棵子樹就可以稱為森林。

前面講到，樹可以理解為是由根結點和若干子樹構成的，而這若干子樹本身是一個森林，所以，樹還可以理解為是由根結點和森林組成的。用一個式子表示為：

Tree =（root,F）

其中，root 表示樹的根結點，F 表示由 m（m >= 0）棵樹組成的森林。

樹的表示方法

除了圖 1（A）表示樹的方法外，還有其他表示方法：

? ? ? ? ? （A） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （B）

圖2 樹的表示形式
?

圖 2（A）是以嵌套的集合的形式表示的（集合之間絕不能相交，即圖中任意兩個圈不能相交）。

圖 2（B）使用的是凹入表示法（了解即可），表示方式是：最長條為根結點，相同長度的表示在同一層次。例如 B、C、D 長度相同，都為 A 的子結點，E 和 F 長度相同，為 B 的子結點，K 和 L 長度相同，為 E 的子結點，依此類推。

最常用的表示方法是使用廣義表的方式。圖 1（A）用廣義表表示為：

(A , ( B ( E ( K , L ) , F ) , C ( G ) , D ( H ( M ) , I , J ) ) )

總結

樹型存儲結構類似于家族的族譜，各個結點之間也同樣可能具有父子、兄弟、表兄弟的關系。本節中，要重點理解樹的根結點和子樹的定義，同時要會計算樹中各個結點的度和層次，以及樹的深度。

什么是二叉樹（包含滿二叉樹和完全二叉樹）

簡單地理解，滿足以下兩個條件的樹就是二叉樹：

1. 本身是有序樹；
2. 樹中包含的各個節點的度不能超過 2，即只能是 0、1 或者 2；

例如，圖 1a) 就是一棵二叉樹，而圖 1b) 則不是。

?

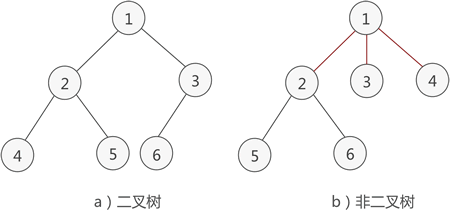
圖 1 二叉樹示意圖

二叉樹的性質

經過前人的總結，二叉樹具有以下幾個性質：

1. 二叉樹中，第 i 層最多有 2i-1?個結點。
2. 如果二叉樹的深度為 K，那么此二叉樹最多有 2K-1 個結點。
3. 二叉樹中，終端結點數（葉子結點數）為 n0，度為 2 的結點數為 n2，則 n0=n2+1。

性質 3 的計算方法為：對于一個二叉樹來說，除了度為 0 的葉子結點和度為 2 的結點，剩下的就是度為 1 的結點（設為 n1），那么總結點 n=n0+n1+n2。
同時，對于每一個結點來說都是由其父結點分支表示的，假設樹中分枝數為 B，那么總結點數 n=B+1。而分枝數是可以通過 n1?和 n2?表示的，即 B=n1+2*n2。所以，n 用另外一種方式表示為 n=n1+2*n2+1。
兩種方式得到的 n 值組成一個方程組，就可以得出 n0=n2+1。

二叉樹還可以繼續分類，衍生出滿二叉樹和完全二叉樹。

滿二叉樹

如果二叉樹中除了葉子結點，每個結點的度都為 2，則此二叉樹稱為滿二叉樹。

?

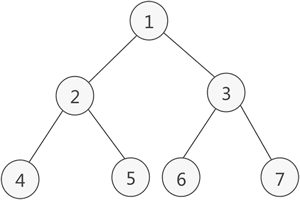
圖 2 滿二叉樹示意圖

如圖 2 所示就是一棵滿二叉樹。

滿二叉樹除了滿足普通二叉樹的性質，還具有以下性質：

1. 滿二叉樹中第 i 層的節點數為 2n-1?個。
2. 深度為 k 的滿二叉樹必有 2k-1 個節點 ，葉子數為 2k-1。
3. 滿二叉樹中不存在度為 1 的節點，每一個分支點中都兩棵深度相同的子樹，且葉子節點都在最底層。
4. 具有 n 個節點的滿二叉樹的深度為 log2(n+1)。

完全二叉樹

如果二叉樹中除去最后一層節點為滿二叉樹，且最后一層的結點依次從左到右分布，則此二叉樹被稱為完全二叉樹。

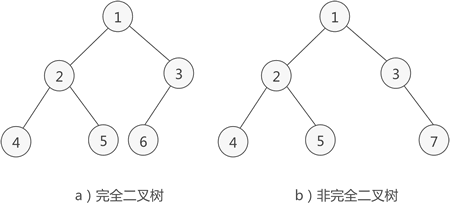
圖 3 完全二叉樹示意圖

如圖 3a) 所示是一棵完全二叉樹，圖 3b) 由于最后一層的節點沒有按照從左向右分布，因此只能算作是普通的二叉樹。

完全二叉樹除了具有普通二叉樹的性質，它自身也具有一些獨特的性質，比如說，n 個結點的完全二叉樹的深度為 ?log2n?+1。

?log2n? 表示取小于 log2n 的最大整數。例如，?log24? = 2，而 ?log25? 結果也是 2。

對于任意一個完全二叉樹來說，如果將含有的結點按照層次從左到右依次標號（如圖 3a)），對于任意一個結點 i ，完全二叉樹還有以下幾個結論成立：

1. 當 i>1 時，父親結點為結點 [i/2] 。（i=1 時，表示的是根結點，無父親結點）
2. 如果 2*i>n（總結點的個數） ，則結點 i 肯定沒有左孩子（為葉子結點）；否則其左孩子是結點 2*i 。
3. 如果 2*i+1>n ，則結點 i 肯定沒有右孩子；否則右孩子是結點 2*i+1 。

二叉樹的順序存儲結構（看了無師自通）

二叉樹的存儲結構有兩種，分別為順序存儲和鏈式存儲。本節先介紹二叉樹的順序存儲結構。

二叉樹的順序存儲，指的是使用順序表（數組）存儲二叉樹。需要注意的是，順序存儲只適用于完全二叉樹。換句話說，只有完全二叉樹才可以使用順序表存儲。因此，如果我們想順序存儲普通二叉樹，需要提前將普通二叉樹轉化為完全二叉樹。

有讀者會說，滿二叉樹也可以使用順序存儲。要知道，滿二叉樹也是完全二叉樹，因為它滿足完全二叉樹的所有特征。

普通二叉樹轉完全二叉樹的方法很簡單，只需給二叉樹額外添加一些節點，將其"拼湊"成完全二叉樹即可。如圖 1 所示：

?

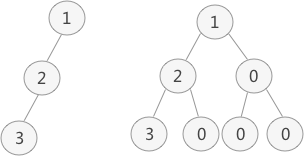
圖 1 普通二叉樹的轉化

圖 1 中，左側是普通二叉樹，右側是轉化后的完全（滿）二叉樹。

解決了二叉樹的轉化問題，接下來學習如何順序存儲完全（滿）二叉樹。

完全二叉樹的順序存儲，僅需從根節點開始，按照層次依次將樹中節點存儲到數組即可。

?

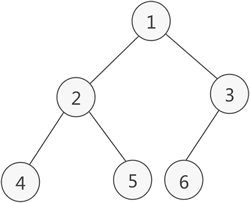
圖 2 完全二叉樹示意圖

例如，存儲圖 2 所示的完全二叉樹，其存儲狀態如圖 3 所示：

?

圖 3 完全二叉樹存儲狀態示意圖

同樣，存儲由普通二叉樹轉化來的完全二叉樹也是如此。例如，圖 1 中普通二叉樹的數組存儲狀態如圖 4 所示：

?

圖 4 普通二叉樹的存儲狀態

由此，我們就實現了完全二叉樹的順序存儲。

不僅如此，從順序表中還原完全二叉樹也很簡單。我們知道，完全二叉樹具有這樣的性質，將樹中節點按照層次并從左到右依次標號（1,2,3,...），若節點 i 有左右孩子，則其左孩子節點為 2*i，右孩子節點為 2*i+1。此性質可用于還原數組中存儲的完全二叉樹，也就是實現由圖 3 到圖 2、由圖 4 到圖 1 的轉變。

二叉樹的鏈式存儲結構（C語言詳解）

本節我們學習二叉樹的鏈式存儲結構。

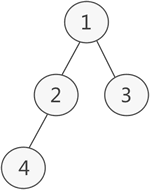
圖 1 普通二叉樹示意圖

如圖 1 所示，此為一棵普通的二叉樹，若將其采用鏈式存儲，則只需從樹的根節點開始，將各個節點及其左右孩子使用鏈表存儲即可。因此，圖 1 對應的鏈式存儲結構如圖 2 所示：

?

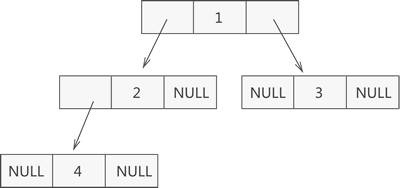
圖 2 二叉樹鏈式存儲結構示意圖

由圖 2 可知，采用鏈式存儲二叉樹時，其節點結構由 3 部分構成（如圖 3 所示）：

• 指向左孩子節點的指針（Lchild）；
• 節點存儲的數據（data）；
• 指向右孩子節點的指針（Rchild）；

圖 3 二叉樹節點結構

表示該節點結構的 C 語言代碼為：

1. typedef struct BiTNode{
2. TElemType data;//數據域
3. struct BiTNode *lchild,*rchild;//左右孩子指針
4. struct BiTNode *parent;
5. }BiTNode,*BiTree;

圖 2 中的鏈式存儲結構對應的 C 語言代碼為：

1. #include <stdio.h>
2. #include <stdlib.h>
3. #define TElemType int
5. typedef struct BiTNode{
6. ??? TElemType data;//數據域
7. ??? struct BiTNode *lchild,*rchild;//左右孩子指針
8. }BiTNode,*BiTree;
10. void CreateBiTree(BiTree *T){
11. ??? *T=(BiTNode*)malloc(sizeof(BiTNode));
12. ??? (*T)->data=1;
13. ??? (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
14. ??? (*T)->lchild->data=2;
15. ??? (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
16. ??? (*T)->rchild->data=3;
17. ??? (*T)->rchild->lchild=NULL;
18. ??? (*T)->rchild->rchild=NULL;
19. ??? (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
20. ??? (*T)->lchild->lchild->data=4;
21. ??? (*T)->lchild->rchild=NULL;
22. ??? (*T)->lchild->lchild->lchild=NULL;
23. ??? (*T)->lchild->lchild->rchild=NULL;
24. }
25. int main() {
26. ??? BiTree Tree;
27. ??? CreateBiTree(&Tree);
28. ??? printf("%d",Tree->lchild->lchild->data);
29. ??? return 0;
30. }

程序輸出結果：

4

其實，二叉樹的鏈式存儲結構遠不止圖 2 所示的這一種。例如，在某些實際場景中，可能會做 "查找某節點的父節點" 的操作，這時可以在節點結構中再添加一個指針域，用于各個節點指向其父親節點，如圖 4 所示：

?

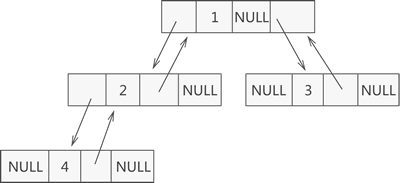
圖 4 自定義二叉樹的鏈式存儲結構

這樣的鏈表結構，通常稱為三叉鏈表。

利用圖 4 所示的三叉鏈表，我們可以很輕松地找到各節點的父節點。因此，在解決實際問題時，用合適的鏈表結構存儲二叉樹，可以起到事半功倍的效果。

樹的雙親表示法

普通樹結構的數據。

?

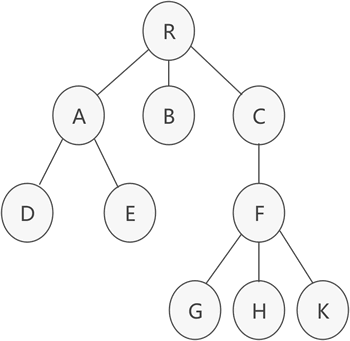
圖 1 普通樹存儲結構

如圖 1 所示，這是一棵普通的樹，該如何存儲呢？通常，存儲具有普通樹結構數據的方法有 3 種：

1. 雙親表示法；
2. 孩子表示法；
3. 孩子兄弟表示法；

本節先來學習雙親表示法。

雙親表示法采用順序表（也就是數組）存儲普通樹，其實現的核心思想是：順序存儲各個節點的同時，給各節點附加一個記錄其父節點位置的變量。

注意，根節點沒有父節點（父節點又稱為雙親節點），因此根節點記錄父節點位置的變量通常置為 -1。

例如，采用雙親表示法存儲圖 1 中普通樹，其存儲狀態如圖 2 所示：

?

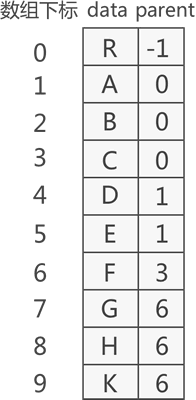
圖 2 雙親表示法存儲普通樹示意圖

樹的孩子表示法

孩子表示法存儲普通樹采用的是 "順序表+鏈表" 的組合結構，其存儲過程是：從樹的根節點開始，使用順序表依次存儲樹中各個節點，需要注意的是，與雙親表示法不同，孩子表示法會給各個節點配備一個鏈表，用于存儲各節點的孩子節點位于順序表中的位置。

如果節點沒有孩子節點（葉子節點），則該節點的鏈表為空鏈表。

例如，使用孩子表示法存儲圖 1a) 中的普通樹，則最終存儲狀態如圖 1b) 所示：

?

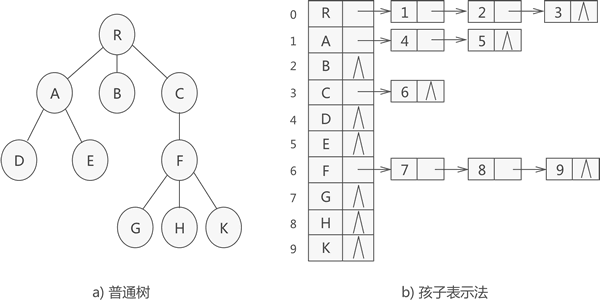
圖 1 孩子表示法存儲普通樹示意圖

圖 1 所示轉化為 C 語言代碼為：

1. #include<stdio.h>
2. #include<stdlib.h>
3. #define MAX_SIZE 20
4. #define TElemType char
5. //孩子表示法
6. typedef struct CTNode {
7. ??? int child;//鏈表中每個結點存儲的不是數據本身，而是數據在數組中存儲的位置下標
8. ??? struct CTNode * next;
9. }ChildPtr;
10. typedef struct {
11. ??? TElemType data;//結點的數據類型
12. ??? ChildPtr* firstchild;//孩子鏈表的頭指針
13. }CTBox;
14. typedef struct {
15. ??? CTBox nodes[MAX_SIZE];//存儲結點的數組
16. ??? int n, r;//結點數量和樹根的位置
17. }CTree;
18. //孩子表示法存儲普通樹
19. CTree initTree(CTree tree) {
20. ??? printf("輸入節點數量：\n");
21. ??? scanf("%d", &(tree.n));
22. ??? for (int i = 0; i < tree.n; i++) {
23. ??????? printf("輸入第 %d 個節點的值：\n", i + 1);
24. ??????? getchar();
25. ??????? scanf("%c", &(tree.nodes[i].data));
26. ??????? tree.nodes[i].firstchild = (ChildPtr*)malloc(sizeof(ChildPtr));
27. ??????? tree.nodes[i].firstchild->next = NULL;
29. ??????? printf("輸入節點 %c 的孩子節點數量：\n", tree.nodes[i].data);
30. ??????? int Num;
31. ??????? scanf("%d", &Num);
32. ??????? if (Num != 0) {
33. ??????????? ChildPtr * p = tree.nodes[i].firstchild;
34. ??????????? for (int j = 0; j < Num; j++) {
35. ??????????????? ChildPtr * newEle = (ChildPtr*)malloc(sizeof(ChildPtr));
36. ??????????????? newEle->next = NULL;
37. ??????????????? printf("輸入第 %d 個孩子節點在順序表中的位置", j + 1);
38. ??????????????? scanf("%d", &(newEle->child));
39. ??????????????? p->next = newEle;
40. ??????????????? p = p->next;
41. ??????????? }
42. ??????? }
43. ??? }
44. ??? return tree;
45. }
47. void findKids(CTree tree, char a) {
48. ??? int hasKids = 0;
49. ??? for (int i = 0; i < tree.n; i++) {
50. ??????? if (tree.nodes[i].data == a) {
51. ??????????? ChildPtr * p = tree.nodes[i].firstchild->next;
52. ??????????? while (p) {
53. ??????????????? hasKids = 1;
54. ??????????????? printf("%c ", tree.nodes[p->child].data);
55. ??????????????? p = p->next;
56. ??????????? }
57. ??????????? break;
58. ??????? }
59. ??? }
60. ??? if (hasKids == 0) {
61. ??????? printf("此節點為葉子節點");
62. ??? }
63. }
65. int main()
66. {
67. ??? CTree tree;
68. ??? for (int i = 0; i < MAX_SIZE; i++) {
69. ??????? tree.nodes[i].firstchild = NULL;
70. ??? }
71. ??? tree = initTree(tree);
72. ??? //默認數根節點位于數組notes[0]處
73. ??? tree.r = 0;
74. ??? printf("找出節點 F 的所有孩子節點：");
75. ??? findKids(tree, 'F');
76. ??? return 0;
77. }

程序運行結果為：

輸入節點數量：
10
輸入第 1 個節點的值：
R
輸入節點 R 的孩子節點數量：
3
輸入第 1 個孩子節點在順序表中的位置1
輸入第 2 個孩子節點在順序表中的位置2
輸入第 3 個孩子節點在順序表中的位置3
輸入第 2 個節點的值：
A
輸入節點 A 的孩子節點數量：
2
輸入第 1 個孩子節點在順序表中的位置4
輸入第 2 個孩子節點在順序表中的位置5
輸入第 3 個節點的值：
B
輸入節點 B 的孩子節點數量：
0
輸入第 4 個節點的值：
C
輸入節點 C 的孩子節點數量：
1
輸入第 1 個孩子節點在順序表中的位置6
輸入第 5 個節點的值：
D
輸入節點 D 的孩子節點數量：
0
輸入第 6 個節點的值：
E
輸入節點 E 的孩子節點數量：
0
輸入第 7 個節點的值：
F
輸入節點 F 的孩子節點數量：
3
輸入第 1 個孩子節點在順序表中的位置7
輸入第 2 個孩子節點在順序表中的位置8
輸入第 3 個孩子節點在順序表中的位置9
輸入第 8 個節點的值：
G
輸入節點 G 的孩子節點數量：
0
輸入第 9 個節點的值：
H
輸入節點 H 的孩子節點數量：
0
輸入第 10 個節點的值：
K
輸入節點 K 的孩子節點數量：
0
找出節點 F 的所有孩子節點：G H K

使用孩子表示法存儲的樹結構，正好和雙親表示法相反，適用于查找某結點的孩子結點，不適用于查找其父結點。

其實，我們還可以將雙親表示法和孩子表示法合二為一，那么圖 1a) 中普通樹的存儲效果如圖 2所示：

?

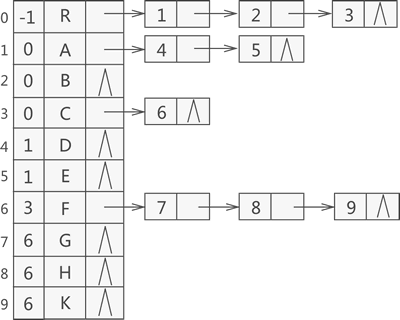
圖 2 雙親孩子表示法

使用圖 2 結構存儲普通樹，既能快速找到指定節點的父節點，又能快速找到指定節點的孩子節點。該結構的實現方法很簡單，只需整合這兩節的代碼即可，因此不再贅述。

樹的孩子兄弟表示法

一種常用方法——孩子兄弟表示法。

?

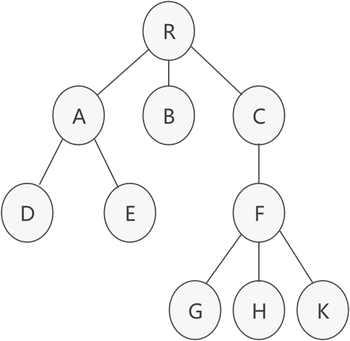
圖 1 普通樹示意圖

樹結構中，位于同一層的節點之間互為兄弟節點。例如，圖 1 的普通樹中，節點 A、B 和 C 互為兄弟節點，而節點? D、E 和 F 也互為兄弟節點。

孩子兄弟表示法，采用的是鏈式存儲結構，其存儲樹的實現思想是：從樹的根節點開始，依次用鏈表存儲各個節點的孩子節點和兄弟節點。

因此，該鏈表中的節點應包含以下 3 部分內容（如圖 2 所示）：

1. 節點的值；
2. 指向孩子節點的指針；
3. 指向兄弟節點的指針；

圖 2 節點結構示意圖

用 C 語言代碼表示節點結構為：

1. #define ElemType char
2. typedef struct CSNode{
3. ElemType data;
4. struct CSNode * firstchild,*nextsibling;
5. }CSNode,*CSTree;

以圖 1 為例，使用孩子兄弟表示法進行存儲的結果如圖 3 所示:

?

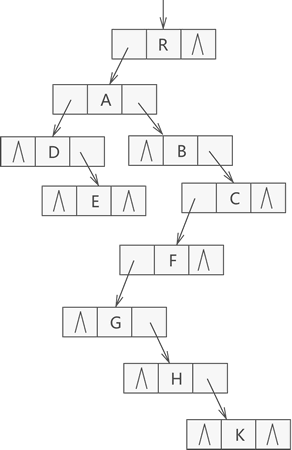
圖 3 孩子兄弟表示法示意圖

由圖 3 可以看到，節點 R 無兄弟節點，其孩子節點是 A；節點 A 的兄弟節點分別是 B 和 C，其孩子節點為 D，依次類推。

實現圖 3 中的 C 語言實現代碼也很簡單，根據圖中鏈表的結構即可輕松完成鏈表的創建和使用，因此不再給出具體代碼。

接下來觀察圖 1 和圖 3。圖 1 為原普通樹，圖 3 是由圖 1 經過孩子兄弟表示法轉化而來的一棵樹，確切地說，圖 3 是一棵二叉樹。因此可以得出這樣一個結論，即通過孩子兄弟表示法，任意一棵普通樹都可以相應轉化為一棵二叉樹，換句話說，任意一棵普通樹都有唯一的一棵二叉樹于其對應。

因此，孩子兄弟表示法可以作為將普通樹轉化為二叉樹的最有效方法，通常又被稱為"二叉樹表示法"或"二叉鏈表表示法"。