2019-08-01 紀中NOIP模擬賽B組

T1?[JZOJ2642] 游戲

題目描述

　　Alice和Bob在玩一個游戲，游戲是在一個N*N的矩陣上進行的，每個格子上都有一個正整數。當輪到Alice/Bob時，他/她可以選擇最后一列或最后一行，并將其刪除，但必須保證選擇的這一行或這一列所有數的和為偶數。如果他/她不能刪除最后一行或最后一列，那么他/她就輸了。兩人都用最優策略來玩游戲，Alice先手，問Alice是否可以必勝？

分析

　　這個說辭...一看就知道是博弈論

　　眾所周知，博弈論有兩個重要結論：

　　1.一個狀態是必敗狀態當且僅當它任意后繼都是必勝狀態

　　2.一個狀態是必勝狀態當且僅當它存在后繼是必敗狀態

　　于是設 $f[i][j]$ 為矩陣為 $i$ 行 $j$ 列時該回合操作方的狀態（$1$ 為必勝，$0$ 為必敗），顯然 $f[1][1]=1$

　　同時需要將 $f[1][i]$ 和 $f[i][1]$ 初始化，還要記錄所有橫軸和縱軸的前綴和

　　然后分別討論刪除最后一行和最后一列時的后繼狀態，若該行或該列無法被刪除，則該后繼視為必勝

　　考場上寫這題的時候已經不早了，感覺有點慌，幸好最后過了

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;
#define N 1005int T, n;
int g[N][N], f[N][N], p1[N][N], p2[N][N];int main() {scanf("%d", &T);while (T--) {scanf("%d", &n);for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++) {scanf("%d", &g[i][j]);p1[i][j] = p1[i][j - 1] + g[i][j];p2[i][j] = p2[i - 1][j] + g[i][j];}f[1][1] = 1;for (int i = 2; i <= n; i++) {int t1, t2;if (p1[1][i] % 2) t1 = 1;else t1 = 0;if (p2[1][i] % 2) t2 = 1;else if (f[1][i - 1]) t2 = 1;else t2 = 0;if (t1 && t2) f[1][i] = 0;else f[1][i] = 1;}for (int i = 2; i <= n; i++) {int t1, t2;if (p2[i][1] % 2) t2 = 1;else t2 = 0;if (p2[i][1] % 2) t1 = 1;else if (f[i - 1][1]) t1 = 1;else t1 = 0;if (t1 && t2) f[1][i] = 0;else f[i][1] = 1;}for (int i = 2; i <= n; i++)for (int j = 2; j <= n; j++) {int t1, t2;if (p1[i][j] % 2) t1 = 1;else if (f[i - 1][j]) t1 = 1;else t1 = 0;if (p2[i][j] % 2) t2 = 1;else if (f[i][j - 1]) t2 = 1;else t2 = 0;if (t1 && t2) f[i][j] = 0;else f[i][j] = 1;}if (f[n][n]) printf("W\n");else printf("L\n");}return 0;
}

T2?[JZOJ2643] 六邊形

題目描述

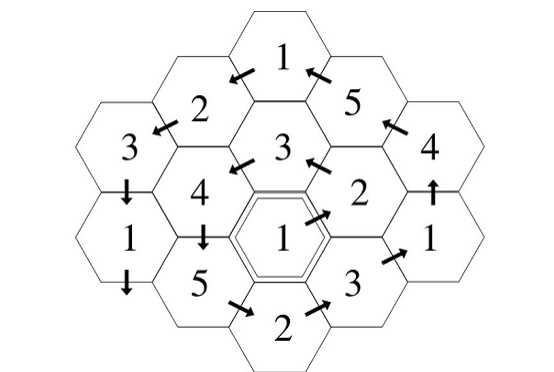
　　棋盤是由許多個六邊形構成的，共有5種不同的六邊形編號為1到5，棋盤的生成規則如下：

　　1.從中心的一個六邊形開始，逆時針向外生成一個個六邊形。

　　2.對于剛生成的一個六邊形，我們要確定它的種類，它的種類必須滿足與已生成的相鄰的六邊形不同。

　　3.如果有多個種類可以選，我們選擇出現次數最少的種類。

　　4.情況3下還有多個種類可以選，我們選擇數字編號最小的。

　　現在要你求第N個生成的六邊形的編號？

　　前14個六邊形生成圖如下：

分析

　　這是個純模擬，感覺沒有什么要分析的

　　主要就是要多注意細節，考場上少寫了一句代碼，直接掉到了 $45.5$ 分

　　而且每次一寫模擬就寫得賊慢

//考場上寫得有點繁瑣
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
#define N 10005int T, n, c = 2, now = 8, s, e, ok, g1, g2;
int q[25], g[N], book[6], sum[6];int main() {scanf("%d", &T);for (int i = 1; i <= T; i++) {scanf("%d", q + i);n = max(n, q[i]);}g[1] = 1; g[2] = 2; g[3] = 3;g[4] = 4; g[5] = 5; g[6] = 2; g[7] = 3;sum[1] = sum[4] = sum[5] = 1;sum[2] = sum[3] = 2; sum[0] = inf;s = 2; e = 7;while (++c) {for (int i = 1; i <= 6; i++) {for (int j = 1; j < c; j++) {memset(book, 0, sizeof book);int minsum = inf;if (j != c - 1) {if (now == e + 1) {book[g[s]] = book[g[e]] = 1;for (int k = 1; k <= 5; k++)if (!book[k])minsum = min(minsum, sum[k]);for (int k = 1; k <= 5; k++)if (!book[k] && sum[k] == minsum) {g[now++] = k; sum[k]++; break;}g1 = s; g2 = s + 1; s = e + 1;}else {book[g[g1]] = book[g[g2]] = book[g[now - 1]] = 1;for (int k = 1; k <= 5; k++)if (!book[k])minsum = min(minsum, sum[k]);for (int k = 1; k <= 5; k++)if (!book[k] && sum[k] == minsum) {g[now++] = k; sum[k]++; break;}g1++; g2++;}}else {if (i == 6) e = now, book[g[s]] = 1;book[g[g1]] = book[g[now - 1]] = 1;for (int k = 1; k <= 5; k++)if (!book[k])minsum = min(minsum, sum[k]);for (int k = 1; k <= 5; k++)if (!book[k] && sum[k] == minsum) {g[now++] = k; sum[k]++; break;}}if (now > n) {ok = 1; break;}}if (ok) break;}if (ok) break;}for (int i = 1; i <= T; i++)printf("%d\n", g[q[i]]);return 0;
}

T3?[JZOJ2644] 數列

題目描述

　　給你一個長度為N的正整數序列，如果一個連續的子序列，子序列的和能夠被K整除，那么就視此子序列合法，求原序列包括多少個合法的連續子序列？

　　對于一個長度為8的序列,K=4的情況：2, 1, 2, 1, 1, 2, 1, 2 。它的答案為6，子序列是位置1->位置8,2->4,2->7,3->5,4->6,5->7。

分析

　　看到題目就先寫了前綴和枚舉區間 $O(n^2)$ 暴力 $30 \, pts$

　　當時看了半天覺得這是最可做的一題，結果看了數據范圍還是沒想出來 $O(n \, log \, n)$ 做法

　　結果考完試下午看了下大家的討論，發現正解是 $O(k)$

　　具體就是把每個前綴和按 $k$ 取模，記錄每個余數出現的次數 $sum$

　　顯然，前綴和所得余數相同的的兩項之間的區間和，一定能被 $k$ 整除

　　所以在余數相同的項中，我們可以任意挑選兩項組成一個合法區間

　　因此答案為 $\sum\limits_{i=0}^{k-1} \binom{sum[i]}{2}$

　　要注意，第 $0$ 項的前綴和余數視為 $0$

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;
#define ll long long
#define N 50005
#define K 1000005int T, n, k, x;
int pre[N], sum[K];
ll ans, c[K];int main() {c[2] = 1;for (int i = 3; i <= N; i++)c[i] = c[i - 1] + i - 1;scanf("%d", &T);while (T--) {ans = 0;scanf("%d%d", &k, &n);for (int i = 1; i <= k; i++) sum[i] = 0;sum[0] = 1;for (int i = 1; i <= n; i++) {scanf("%d", &x);pre[i] = (pre[i - 1] + x) % k;sum[pre[i]]++;}for (int i = 0; i < k; i++)ans += c[sum[i]];printf("%lld\n", ans);}return 0;
}